刚体转动惯量的测定

施洪琼,山朝恒,瞿发钦,吴艳梅,马雪霞,高全归

(玉溪师范学院 物理与电子工程学院，云南 玉溪 653100)

转动惯量是刚体绕轴转动时惯性的量度，其值由物体的形状、质量分布、转轴位置3方面的因素共同决定[1，2].转动惯量在科学实验、工程技术、航天、电力、机械等工业领域有着重要的应用，是一个重要参量.在汽车制造中，转动惯量是发动机本体以及整体设计的重要参数，在气缸内工作压力、平均指示压力等参数的估算中有着非常重要的作用[3].测量转动惯量的方法有多种，如复摆法，三线扭摆法等[4].采用复摆法测量转动惯量，在摆角过大的时候，测量精度显著降低，当摆角大于60°时，测量误差超过40%[5].三线摆具有操作简单，准确度高的特点，但对于大质量物体的测量非常不方便[5,6].采用扭摆法测量刚体的转动惯量，其误差比三线摆还小[7].三线摆法测量刚体转动惯量的精度比扭摆法更高[8,9].在本文中，笔者在常用测量转动惯量的方法的基础上进行改进，用其测量不规则刚体的转动惯量，并分析实验存在的问题和改进方向.

1 实验仪器、方法和实验原理

1.1 实验仪器和方法

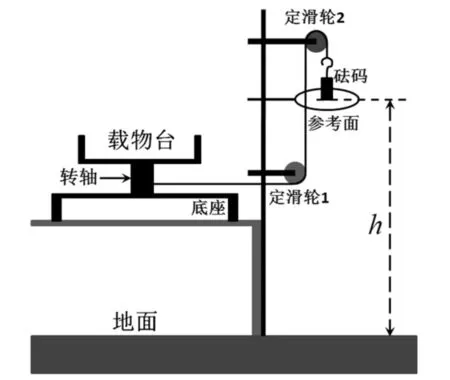
图1 转动惯量测定实验装置示意图

图1为本文所使用的转动惯量测定实验装置的示意图.实验时，细线的一端缠绕在转轴上，细线绕过两个定滑轮，另一端挂有砝码.待测物放在载物台上并固定，载物台和转轴固定在一起且不能有相对转动，转轴相对于底座转动，并且应尽量让转轴和底座连接处的转动摩擦力小.砝码的重力带动转轴和载物台转动，砝码、细线、转轴和载物台构成的系统由细线连接，因而线加速度是相同的.

本实验装置在传统的实验装置中加入了定滑轮2和参考面.实验中，细线先绕过定滑轮1，然后绕过定滑轮2，是为了增加砝码运动的距离以提高实验精度.加入参考面是为了砝码静止时所在的位置有一个确定的参考面，使得实验更为方便，也能提高精度.传统的实验直接让细线从定滑轮1的上方向下并挂有砝码，没有设置砝码静止点的参考面，实验中砝码行走的距离较短，砝码静止点的参考位置不好选定.

实验过程中，让砝码自由下落，记录下砝码从参考面到地面所用的时间，由于采用秒表测量时间误差较大，需要反复测量多次.同时，为了得到M-α函数关系，还需要改变砝码质量多次，并测量相应下落时间.计算角加速度需要测量出参考面与地面的距离，为了得到拉力矩还需要测量转轴的半径.

1.2 实验原理

根据刚体转动定律，转动系统所受合外力矩M和与角加速度α的关系为[10]：

M和=Iα，

(1)

其中I表示转动惯量，为待测物理量，α为转动物体的角加速度，M和表示合外力矩，主要由引线的张力矩M拉[11]和物体间摩擦力矩M阻构成，它们的关系为M和=M拉+M阻，代入(1)式得：

M和=M阻+Iα，

(2)

上式中，I为系统对转轴的转动惯量，摩擦力矩M阻是未知的，并且很难测量，但它主要来源于接触摩擦，可认为是恒定的.引线所受到的张力FT就是砝码的重力mg，将转轴的半径用R来表示，则载物台和待测物体一起所受的拉力矩为：

M拉=mgR，

(3)

由(3)式可见，确定砝码的质量，并测量得到转轴的半径R后就可以计算出转台所受的拉力矩.

由于转台和砝码之间由引线连接，因此，砝码的线速度和转轴上所绕引线的速度是一致的，也就是转轴外边缘的线速度和砝码的线速度相同，对应的线加速度也就是一致的.砝码下落的过程是一个匀加速运动，砝码运动的距离为h，所需要的时间t由实验测量得到，可以计算得带线加速度a为：

(4)

利用线量和角量的关系，可以得到转台的角加速度α为：

(5)

多次改变拉力，并测量相应的砝码下落时间，通过计算就可以得到一组M拉-α的数据，利用最小二乘法，可以计算得到转台和待测物体的转动惯量I总.

由于(2)式是一个线性关系式，因而，为了得到待测物的转动惯量，只需要在I总的基础上减去转台的转动惯量I空，就可以得到待测物的转动惯量.

2 实验数据处理

2.1 实验数据

实验中分别考虑3种情况，(1)空载；(2)在载物台上加上一个圆环；(3)在载物台上加上一个不规则的待测物体.空载是为了计算转台的转动惯量I空；加圆环时，可以通过理论计算得到圆环的转动惯量，并与实验结果进行比较，以验证转动惯量的正确性；对于情况(3)，则是为了测量任意待测物体的转动惯量.实验过程中的测量结果由表1及原始数据记录给出.

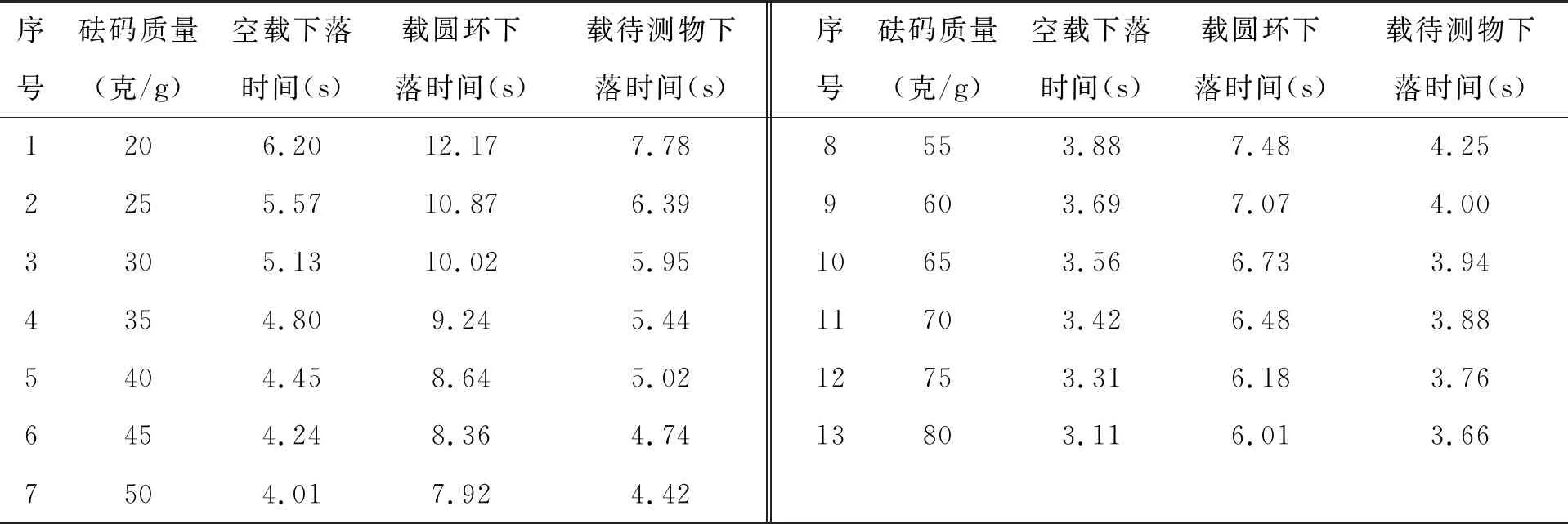
表1 砝码下落过程的时间测量

测量结果都进行了多次测量，计算中舍弃了高度异常值，在此不将测量结果一一列出，且仅给出最后计算出来的平均值.

原始数据记录：规则物体(圆环)的内径D内,17.56 cm;外径D外,19.74 cm;质量m,482.66 g;绕线转轴的直径d,5.02 cm;参考面离地面的高度及砝码的下落距离h,147.50 cm.

2.2 转动惯量测定

利用空载，加圆环和加不规则物体时的实验数据，分别计算得到一组M拉-α数据，见表2.运用最小二乘法，可以得到转动惯量I和阻力矩M阻，事实上M阻是可以直接由最小二乘法的结果得到，这也是实验中不计算或测量滑轮的转动惯量、阻力和阻力矩的原因.

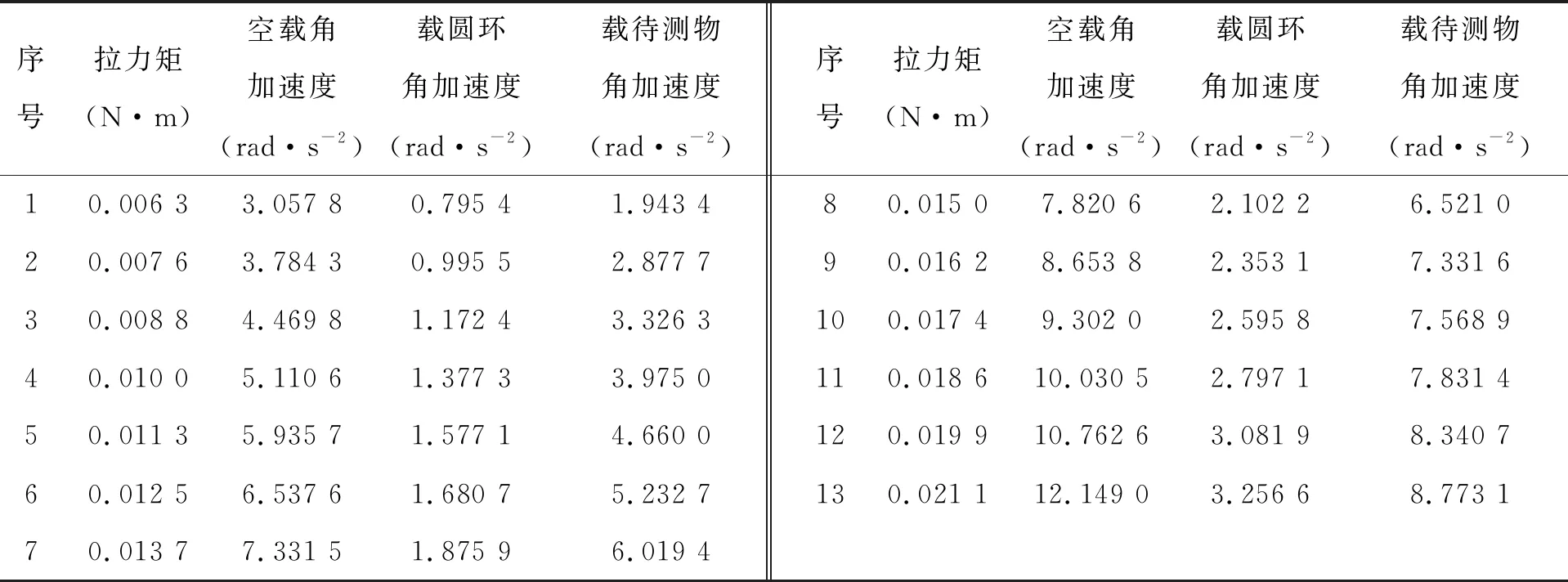
表2 拉力矩和角加速度的计算结果

图2给出了空载时实验数据的最小二乘拟合结果，黑色正方形为实验数据，直线为拟合结果，直线的斜率就是空载的转动惯量I空，截距则表示阻力矩M阻.由图2的拟合结果可知：I空=0.001 70±0.000 03=(1.70±0.03)×10-3kg·m2，M阻=(1.2±0.3)×10-3N·m.

图3表示加规则物体(圆环)时实验数据的最小二乘拟合结果，与图2一样，黑色正方形为实验数据，直线为拟合结果，直线的斜率是载物台和圆环的总转动惯量I总，截距则表示阻力矩M阻.

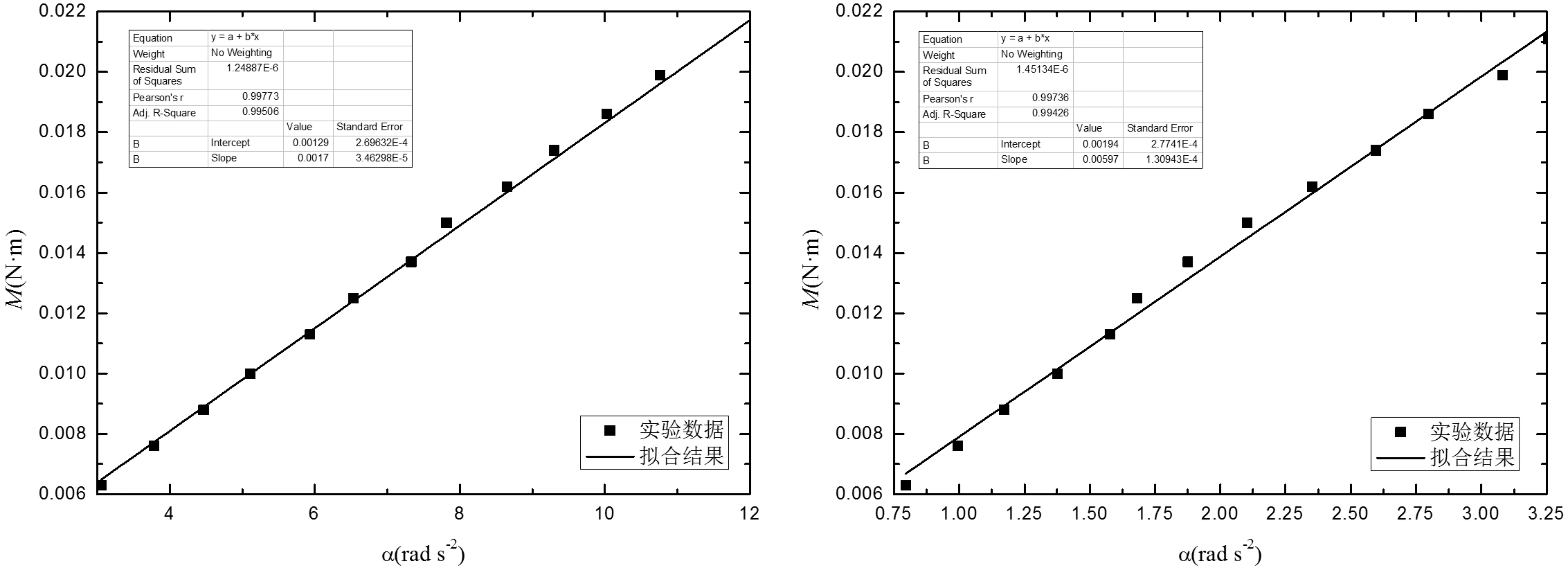
图2 空载时的M拉-α直线拟合结果 图3 加圆环时的M拉-α直线拟合结果

由图3的结果可知：I总=0.005 97±0.000 13=(5.97±0.13)×10-3kg·m2，M阻=(1.94±0.28)×10-3M·m.结合图2的结果可得圆环的转动惯量为：

I环=I总-I空=(4.27±0.16)×10-3kg·m2.

(6)

为了验证实验结果的正确性，在此，根据理论力学的方法计算圆环的转动惯量I圆，根据圆环的转动惯量计算公式：

(7)

由于圆环的内径和外径由游标卡尺测量结果，计算中会导致误差的传递，圆环内径的测量误差为：

(8)

其中，uA(D内)表示内径测量的A类分量，简单计算就可得到uA(D内)≈1.38×10-4m，内径不确定度的B类分量uB(D内)≈5.77×10-4m.同样的方法可以得到圆环外径的测量不确定度为：

(9)

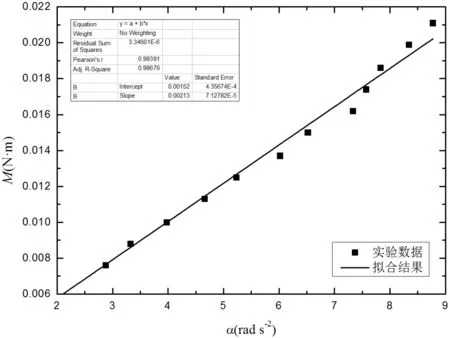
图4 加不规则物体时的M拉-α直线拟合结果

其中：uA(D外)≈1.70×10-4m，uB(D外)≈5.77×10-4m，利用(7)(8)式，根据误差理论计算得到圆环转动惯量的不确定度为：

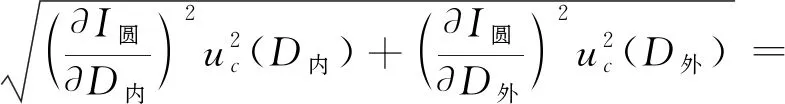
0.02×10-3kg·m2，

(10)

于是，计算得出圆环的转动惯量为：

I圆=(4.21±0.02)×10-3kg·m2.

(11)

比较式(6)和式(11)两种转动惯量的测量结果，可知在测量圆环的转动惯量时，本文所采用的实验方法所测得的转动惯量比测量圆环的内外径后进行计算得到的转动惯量还要精确.

图4给出了不规则物体转动惯量实验数据的最小二乘拟合结果，与图2一样，黑色正方形为实验数据，直线为拟合结果，直线的斜率是载物台和圆环的总转动惯量I总，截距则表示阻力矩M阻，由图3的拟合结果可知：I总=(2.13±0.07)×10-3kg·m2，相应的阻力矩则为：M阻=(1.52±0.44)×10-3N·m.结合图2的结果可得待测物的转动惯量为：I=I总-I空=(0.43±0.10)×10-3kg·m2.

2.3 阻力矩与转动惯量的关系

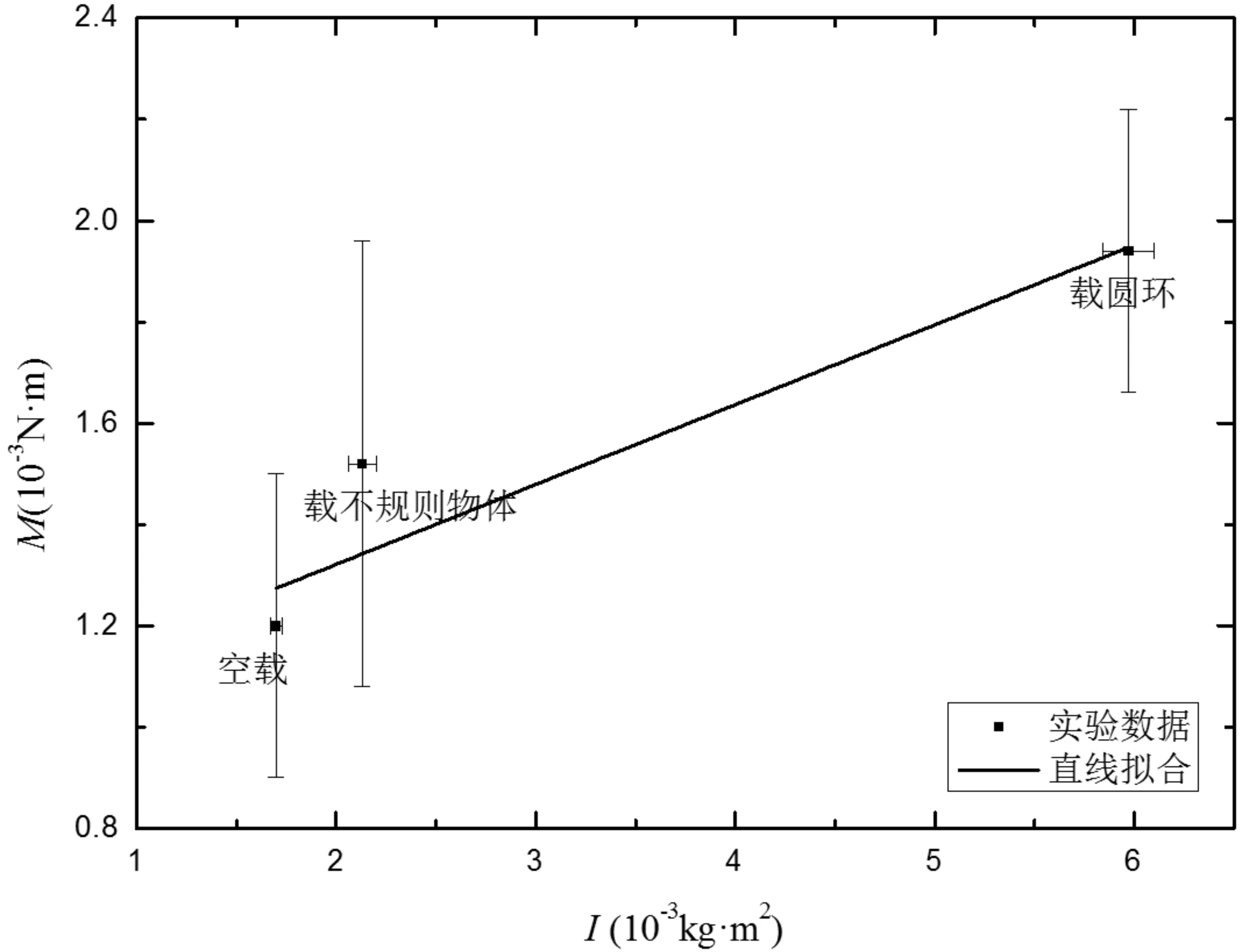
图5 转动惯量I总和阻力矩M阻之间的函数关系

图5由表3的数据得到，由图5可知，总的转动惯量越大，则对应的阻力矩越大，相应转动惯量的测量误差也大，这表明转动惯量较大的物体转动时，由于转动而产生的摩擦力也越大，这些摩擦力就是产生阻力矩的原因.但阻力矩的误差则可能与待测物的形状及转动轴相对待测物体的位置有关，对于规则物体，转轴在其质心，此时，连接载物台与底座的转轴所受的压力是均匀的，因而，此时产生的阻力矩不大.如果待测物体不规则，且转动轴不经过待测物的质心，此时，连接载物台与底座的转轴所受的力就不均匀，这个不均匀的受力可能使得相对转动轴有一个额外的力矩，这个力矩就是一个阻力矩，因而测量不规则物体的时候反而会出现较大的阻力矩.

3 结论及讨论

本文在传统的转动惯量实验仪器的基础上对实验装置进行了改进，增加了砝码下落的高度.改进后的实验结果表明，采用本装置测量规则物体(圆环)的转动惯量，其测量精度高于采用游标卡尺测量圆环内外径后的计算结果.本实验装置不仅可以测量规则物体的转动惯量，也能测量不规则物体的转动惯量.测量中，总的转动惯量越大时对应较大的阻力矩，相应转动惯量的绝对误差也变大，其相对误差不发生明显变化.这样的实验结果表明，转动惯量较大的物体转动时，由于转动而产生的摩擦力也越大，这些摩擦力就是产生阻力矩的原因.但阻力矩的误差则可能与待测物的形状及其与转动轴相对待测物体的位置有关，对于规则物体且转轴在其质心时，连接载物台与底座的转轴所受的压力是均匀的，因而产生的阻力矩不大.如果待测物体不规则，且转动轴不经过待测物的质心，那么连接载物台与底座的转轴所受的力就不均匀，这个不均匀的受力可能使得相对转动轴有一个额外的力矩，因而测量不规则物体的时候反而会出现较大的阻力矩.

为使测量更为精确，还可以对实验装置做进一步改进.由实验结果可以看出，阻力矩的大小对于实验精度的影响较小，降低实验精度的原因在于测量过程中连接载物台和底座的转轴受力不均匀.为了解决这一问题，可以在转轴与底座之间用滚珠轴承加以连接，在载物台和底座之间也加上有支撑作用的滚珠轴承.这样的实验改进会增加阻力矩，但是能保证阻力矩沿转动轴均匀分布，实验中只需要增加砝码的质量来提高拉力矩就能够顺利完成实验.