“截面法”与三重积分的计算

刘菊青

(玉溪师范学院 数学与信息技术学院,云南 玉溪 653100)

在直角坐标系下化三重积分为三次积分一直是多元函数积分学中的一个学习难点，推导过程形式抽象,理解困难，再加上对积分区域图形的认知难度，使其成为学习的一个难点.然而，这个推导过程又是及其重要的，它是化三重积分为柱面坐标和球面坐标下的三次积分计算的基础.如何突破三重积分学习上的难点一直是值得思考与研究的问题.为此，本文通过研究“截面法”计算三重积分，获得了一种嫁接实际意义推导三重积分计算的方法，有助于三重积分学习的突破，理解三重积分计算的原理和数学实质，利于三重积分计算方法的掌握.

1 累次积分法的简单回顾

图1 三重积分区域图

s1:z=z1(x,y),s2:z=z2(x,y),

函数z1(x,y)与z2(x,y)都是Dxy上的连续函数，且z1(x,y)≤z2(x,y，则三重积分化为一个单次积分和一个二重积分，即

再将二重积分化为两个单次积分即可.若Dxy表示为

Dxy:a≤x≤b,y1(x)≤y≤y2(x)，

则三重积分最终化为三次积分

上述计算三重积分的方法称为累次积分法,其实质就是将三重积分最终转化为三次积分计算.

三重积分在直角坐标下的累次积分法反映的是高度抽象化的计算过程，它实质是三重积分计算方法的一般化归纳过程，大多数微积分学的教材中给出的三重积分的计算均是上述方法，并未揭示它是如何得出的？这就造成对三重积分计算认知的困难.因此，有必要揭示三重积分在直角标下的实质性的推导计算过程.

2 利用实际意义推导计算三重积分

我们不妨作这样的思考：从积分概念推广的角度，既然定积分的微元法和二重积分的计算均可根据其几何意义即实际意义推导得出，那么是否可以思考三重积分计算也可以通过其实际意义来推导？

在重积分概念建立的过程中有两个实际问题：非均匀薄片的质量和非均匀物体的质量.非均匀薄片质量问题的求解是二重积分概念建立、理解及二重积分应用的基础，非均匀物体质量问题的求解是三重积分概念引入的实例.在多数微积分教材内容中均有此实例. 既然非均匀薄片质量问题的求解可以用微元法转化为二重积分的计算问题，那么三重积分的计算也可以利用非均匀物体质量问题求解来推导.

2.1 “截面法”推导三重积分的计算

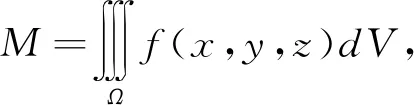
图2 截面法示意图

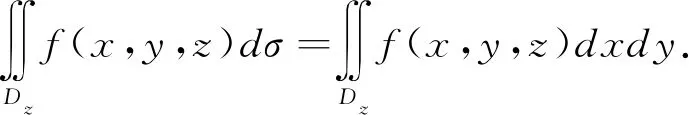
其次，再过z轴上的点z+dz∈[a,b]，作垂直于z轴的平面截区域Ω，则区间[z,z+dz]所对应的小块薄片的质量微元

将这些小块薄片的质量相加便得到物体质量M,故

进而得

上述计算三重积分的方法称为“截面法”.同理可推导

其中,Dx为夹在两平行平面x=c,x=d之间的任意垂直于x轴的平面,截积分区域Ω所得的平面区域在yoz坐标面上的投影区域.同样,Dy为夹在两平行平面y=e,y=f之间的任意垂直于y轴的平面,截积分区域Ω所得的平面区域在xoz坐标面上的投影区域.

截面法的实质就是利用三重积分的实际意义，将三重积分化为先二重积分，后定积分的顺序计算的方法.理论上，截面法是一般化的通用方法，但由于区域Dz的复杂性，它适用于解决较为简单的、特殊的积分区域Dz的三重积分的计算.这一方法也使我们得到启发，三重积分的计算是可以利用实际意义来推导的.

2.2 利用实际意义推导的累次积分法

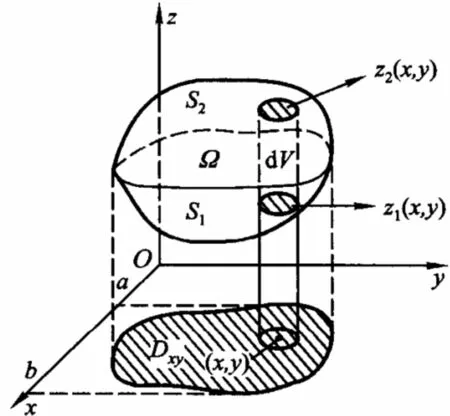
图3 累次积分法示意图

如图3，积分区域Ω在xoy面上的投影区域为Dxy，上、下曲面分别为s2:z=z2(x,y)和s1:z=z1(x,y),(x,y)∈Dxy.在Dxy任取一个小区域σ，以区域σ为底、母线平行于z轴的柱面截区域Ω，在Ω内截得小柱体ΔΩ，在z轴上任取两点z和z+dz，用过这两点且垂直于z轴的平面截小柱体ΔΩ得一小物体段，该小物体段的质量用Δm表示，用如下方法近似计算：

该小物体段体积用ΔV表示，在xoy面上的投影区域σ的面积用Δσ表示，则小物体段体积

ΔV=Δσ·dz，

又用在点(x,y,z)((x,y)∈σ)的密度近似为该小物体段的平均密度，从而得该小物体段的质量

Δm≈f(x,y,z)·ΔV=f(x,y,z)·Δσ·dz(质量=密度×体积).

由上述近似计算的方法，若取面积微元dσ，并用dV表示体积微元，则Δσ≈dσ，dV=dσ·dz，.由此得出小物体段的质量

Δm≈f(x,y,z)·dσ·dz=f(x,y,z)·dz·dσ

再由z的任意性，[z,z+dz]⊂[z1(x,y),z2(x,y)]，得出小柱体ΔΩ对应的物体质量微元

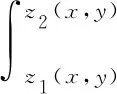
又由σ的任意性，σ⊂Dxy，将每个小柱体的质量相加，便得所求空间物体的质量

上述等式的右端表示先计算关于z的定积分，然后再计算在区域Dxy上的二重积分.为了书写方便，上式可写作

因此，我们就将三重积分化为先计算一个定积分，在计算一个三重积分的公式

若Dxy=(x,y)|a≤x≤b,y1(x)≤y≤y2(x),则三重积分最终化为三次积分

这就是由实际意义推导的三重积分计算的累次积分法.

2.3 利用实际意义推导计算三重积分的意义

上述的两种三重积分计算的推导方法，均借助三重积分的实际意义即非均匀物体的质量来推导，揭示了三重积分计算公式的来历，明确了三重积分计算的本质内涵.同时，这一问题的解决过程从实质上也揭示了从二重积分概念、计算到三重积分的概念与计算的推广，使我们明确数学应用及其价值.更深层次地看，首先，从非均匀物体质量问题的提出到三重积分的概念，再到三重积分计算推导，最终明确这一问题的完整解决的过程，体现是问题解决的数学模型思想与方法.其次，再次诠释二重积分和三重积分应用的微积分思想和方法，进一步体会微元法在微积分应用问题解决中的重要性.这也就是微积分教学应该传递给学生的数学实质和微积分学的价值与学习意义.

3 利用截面法计算三重积分举例

三重积分计算的累次积分法是广泛使用的一般性方法，微积分学习中以掌握这种计算方法为主，而截面法只是通过少数的实例进行介绍，对如何利用截面法计算三重积分在微积分学的教材中并未深层次解析.截面法因为会受到截面区域Dz的限制，因此只能在特殊情形下使用，下面就通过几个典型的例子进行解析归纳，使我们明确满足什么特殊情形可以使用截面法.

图4 例1的积分区域图

解析这是利用截面法计算三重积分的一个非常简单的例子，其特点是被积函数是一个单变量函数，积分区域Ω是平面x+y+z=1与三坐标面围成的四面体(如图4).区域Ω满足0≤z≤1,任取z∈[0,1]，用垂直于z轴的平面截Ω，所得的截面区域是一个三角形,在xoy平面上的投影区域Dz由xoy面上的直线x+y=1-z(z看为常量)与两坐标轴x=0,y=0围成的三角形区域，则由截面法得

当然，此题也可以采用累次积分法.由积分区域Ω可表示为

Ω:0≤x≤1,0≤y≤1-x,0≤z≤1-x-y,

原式化为

按照此法计算,积分过程显然要比用截面法计算复杂得多.因此,在计算此题时,截面法有其简便之处.

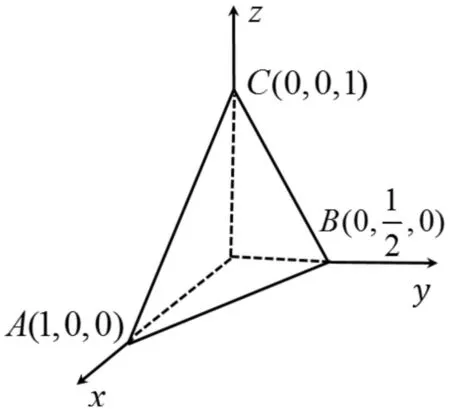
图5 例2的积分区域图

解析此题的特点同例1，被积函数依然是单变量函数,积分区域Ω仍然为四面体(如图5),满足0≤x≤1,任取x∈[0,1],用垂直于x轴的平面截Ω,所得的截面区域是一个三角形,在yoz平面上的投影区域Dx由yoz面上的直线2y+z=1-x(x看做常量)与两坐标轴y=0,z=0围成的三角形区域,因此可用截面法计算，则

代入上述积分,可得

此题依然可以采用累次积分法计算，只是积分计算的过程与截面法相比，较为复杂，具体的计算过程就不详细介绍了.

通过以上两例，可以看出，如果被积函数为单变量函数，且截面区域可以计算面积，则采用截面法会较为简便.

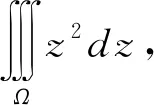
图6 例3的积分区域图

解析此题被积函数依然是单变量函数，积分区域与前面两例的要复杂一些，是一个椭球体(如图6).截面投影区域Dz实质是椭圆围成的区域,

此区域是可以计算面积的.用截面法化三重积分

截面法计算此三重积分，思路清晰，计算简便，若此题要使用累次积分法计算,估计是困难的.

解析因为被积函数是含单个变量z的函数,积分区域又由两球面x2+y2+z2≤2rz和x2+y2+z2≤r2所围成的，截面区域投影Dz是圆域，可计算面积，所以可采用截面法计算.又由于在两个球面上截得的圆域不同,所以此三重积分的计算需要划分区域，利用区域可加性计算.可设在两个球面上的截面投影区域分别为

所以三重积分化为

又

所以

此题如果想要利用累次积分法计算，是极其困难的.

限于篇幅，截面法计算三重积分还未详尽，实质上截面法不仅是在直角坐标下运用，也可以推广到柱面坐标和球面坐标计算三重积分，还可以根据被积函数的特点，使用坐标变换法使积分计算简化. 通过上面最后一例也可以看出，有时还需配合使用积分的性质.当然，截面法的使用也存在局限，当被积函数或者积分区域复杂导致积分的困难以及计算截面投影区域面积的困难时，就不适合使用.总之，要灵活掌握截面法的运用，最根本的问题是弄懂截面法计算三重积分的实质.