一种适用于大偏心率轨道密集星历精密计算的快速处理方法∗

戴志军 徐 劲

(1中国科学院紫金山天文台南京210023)(2中国科学院大学北京100049)(3中国科学院空间目标与碎片观测重点实验室南京210023)

1 引言

随着人类航天活动的日益频繁,空间目标和碎片的数量越来越多,根据NASA(National Aeronautics and Space Administration)编目库的最新发布结果,目前10 cm以上的空间目标和碎片大约为2万颗.未来对空间碎片的探测将拓展到更小尺寸,能够探测到的空间碎片数量还会进一步增长,预计可探测的空间碎片数量将达到20万颗,这些弥漫在近地空间的目标和碎片对在轨工作的航天器具有潜在的威胁[1],其中1 cm以上的碎片对航天器的损伤是致命的,因此日益增长的空间目标和碎片对人类航天活动的安全提出了严峻挑战.

为了有效规避或减小空间目标和碎片的潜在威胁,提升在轨航天器工作的安全性,需要对空间目标和碎片的运动态势进行精确掌控,这就是通常意义上的空间目标编目和管理,它本质上是一个基于空间目标观测资料进行轨道确定、轨道预报和轨道更新的动态循环过程,涉及一系列复杂的轨道计算处理.由于空间目标和碎片的数量巨大,编目工作中的轨道计算有别于一般应用中的轨道计算,不仅要求轨道计算的精度,轨道计算的效率也是一个不容忽视的关键因素,编目工作对轨道计算效率的最低要求是确保轨道计算的整体处理时间不大于观测设备的数据采集时间以避免产生观测数据积压的瓶颈效应,使编目过程难以持续.因此,当前编目工作中的轨道计算广泛采用分析方法,分析方法计算速度快,用于编目处理是非常有利的.但随着观测技术的发展,它的轨道计算精度(模型误差数百米)并不能与当前的观测精度相匹配,从而不能达到理想的编目定轨精度,制约了相关应用水平的提升,因此数值方法在编目工作中仍具有潜在的应用价值.

在空间目标的编目工作中,数值方法能实现较高的轨道计算精度,但相应的轨道力学模型即积分右函数较为复杂[2],因此评价数值方法计算效率的主要指标体现为一次轨道计算过程中所需计算的右函数次数.编目工作的轨道计算过程普遍涉及密集星历的产生和计算问题,在这种情形下如采用对各个星历时刻逐点积分的方式,因星历点分布密集,积分步长不能得到充分伸展,右函数计算次数将大大增加,严重降低数值计算方法的效率.避免这一困难的有效技术手段就是在计算过程中运用内插方法,即首先在轨道上选择一系列间隔较为稀疏的基点,基点上的星历值由数值积分得到,其他点上的星历值由基点上的星历值插值得到,这样的处理方式具有极高的计算效率,从而可大幅提升数值方法用于编目处理的计算效率,使之更好地满足编目工作对处理时效的要求.

关于精密密集星历的产生,目前基于各种内插方法已有广泛的研究[3–5],但已有的工作基本都是针对运动特征变化非常平缓的近圆小偏心率轨道.如黄天衣等[6–7]提出了一种改进型的具一次和分形式的Adams-Cowell方法,不仅包含积分公式,而且包含与之在精度上相配套的内插公式.具体应用时,可由积分公式得到一系列间隔均匀(以积分步长为间隔)步点上的星历值,其他点上的星历值可在积分过程中由内插公式得到,由于Adams-Cowell方法对当前步点的积分计算可继承之前各步点上的历史信息,使得该方法每步积分最多只需计算2次右函数值,因此计算效率极高.但由于采用定步长积分,局部截断误差得不到有效控制,且由于数值稳定性等原因,该方法同样不适用于运动特征变化较为剧烈的大偏心率(经验推定偏心率e>0.2)轨道计算.不过由于在编的各类空间目标轨道大部分为小偏心率轨道,因此Adams-Cowell方法的运用仍可在整体上大大提升编目处理的时效.

虽然大偏心率轨道在空间目标中占比不高,但由于空间碎片数量巨大且增长迅速,因此大偏心率轨道编目处理的时效性问题仍不容忽视.在各类数值积分方法中,单步法由于能够在积分过程中灵活地改变步长,通过每步的步长变化有效控制局部截断误差,从而适用于大偏心率轨道的精密星历计算.但单步法在积分过程中每步所需计算的右函数次数较多,且一般的单步法并无与积分公式相配套的插值公式.少数单步法,如一些阶次的Runge-Kutta类方法[8],虽有配套的插值公式,但积分处理过程较为复杂,若只局限于这些少数方法,还限制了其他多种方法的优化选择和使用便利性,因此在编目工作中,针对大偏心率轨道的密集星历计算问题,不宜单纯使用单步法进行积分,否则易于导致计算效率低下.

针对以上的问题和困难,为了进一步提升编目处理的时效,本文提出了一种适用于大偏心率轨道密集星历精密计算的快速处理方法,该方法的核心技术是构建了一种全新的内插方法,该内插方法可以与一般的单步积分法在星历计算过程中协调使用,同时满足大偏心率轨道密集星历计算的高精度和高时效要求.

2 精密高效星历计算方法

2.1 插值基点构造方法

空间目标主要受地球质心的引力作用,其他均为摄动影响,相对于地球质心引力而言,它们都是1阶或2阶小量,因此以下将空间目标运动考虑为绕地球质心的2体运动,其轨道是一个定常的椭圆轨道.这样的简化方式有助于理论推导和说明,也不会对问题的结论产生本质影响.实际上算法实用性在摄动情形下同样适用且本文数值模拟结果基于摄动模型.

在密集星历计算中采用内插方法是提高计算效率的有效手段,这一技术手段已在导航星广播星历计算中得到广泛应用,但在导航星历计算中普遍采用了均匀间隔的插值基点,即有:

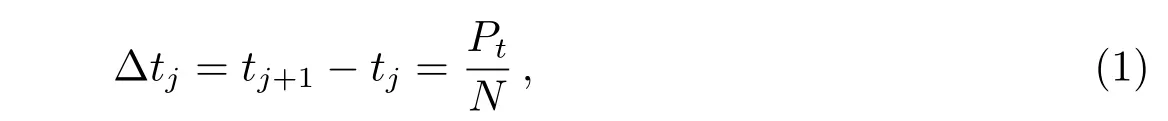
其中tj(j=1,2,3,···)是一系列均匀间隔的插值基点,Pt是以时间变量t计量的轨道运动周期,N为一个轨道周期含有的基点数量,∆tj为第j个基点至第j+1个基点的时间间隔.这一基点划分方式并不适用于编目工作中可能遇到的大偏心率轨道计算,其主要原因是大偏心率轨道近地点和远地点附近目标运动状态差异较大,在近地点附近目标运动变化非常剧烈,在远地点附近目标运动变化非常缓慢,若采用均匀间隔的插值基点,则近地点附近星历插值误差远大于远地点附近星历插值误差.为了避免以上缺陷,本文基于Sundman变换的均匀化思想[9–10],引入一个伪时间变量τ,按τ进行均匀间隔的基点划分,并构建τ和t的变换关系为:

其中r为目标地心距,a为轨道半长径,δ是一个常量,其取值方式将在下文交待.

设E为目标偏近点角,将椭圆运动关系

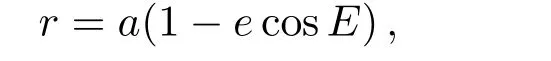
代入变换关系式(2)式可得:

设n为目标平均运动角速度,M为目标平近点角,t0为目标过轨道近地点时刻,对开普勒方程:

两边同时微分并整理可得:

由(3)式和(4)式可得

设Pτ为以伪时间变量τ计量的轨道运动周期,τ0为目标过轨道近地点的τ时刻,对(5)式两端同时积分一个轨道周期,即有:

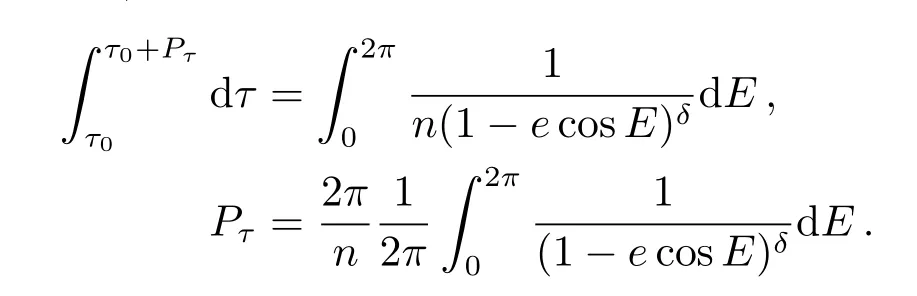
由椭圆运动关系Pt=2π/n,并设:

即得到:

α是一个常量,与轨道偏心率e和δ的取值相关,在星历计算中,α值可采用任意定积分计算方法得到.

按变量τ进行均匀间隔的基点划分,得到一系列的插值基点τj(j=1,2,3,···),与其对应的按时间t划分的插值基点为tj(j=1,2,3,···),假定一个轨道周期含有的基点数量仍为N,则第j个基点τj至第j+1个基点τj+1的间隔为:

将(6)式代入(7)式可得:

将(2)式两端同时积分:

并利用中值定理可得到:

(9)式中rξ=r(tξ),tξ为tj和tj+1之间的某个值,如果以时间尺度τ按(9)式对一个轨道周期进行严格划分,则相应地也将同一个轨道周期在时间尺度t下划分为N个长度不均匀的间隔,但是tξ的值不能确定,因此不能进行实际的划分,所以本文转而定义:

(10)式中

当已知tj时,rj的值可由积分得到,按(10)式容易得到tj+1,即采用(10)式确定了一种可实际使用的基点划分方式.

由于(10)式和(9)式存在差异,因此按(10)式进行按时间t划分时,一个轨道周期含有的基点数量一般不为N.但大量的数值实验结果表明,基于通常的星历精度要求,对于大偏心率轨道计算,所需的N值往往较大,相应的基点间隔较小,(10)式近似等同于(9)式,对于小偏心率轨道计算,虽然所需的N值不大,但此时rj的变化较小,其值基本保持恒定,(10)式也近似等同于(9)式,因此采用(10)式进行基点划分,其一个轨道周期的基点数量大致为N.

将(8)式代入(10)式,进一步可得到:

采用(11)式进行基点划分,一般可得到一系列非均匀间隔的插值基点tj(j=1,2,3,···),且一个轨道周期的基点数量大致为N.

由α的计算公式和椭圆运动关系式可知,当e=0或δ=−1时,(11)式退化为(1)式,即采用均匀间隔基点划分.此外不难证明:当δ=0时,(11)式等同于按目标偏近点角E进行的均匀间隔基点划分;当δ=1时,(11)式等同于按目标真近点角进行的均匀间隔基点划分.

当δ>−1时,相比于(1)式确定的均匀间隔基点,由(11)式确定的插值基点在近地点附近分布较为密集,在远地点附近分布较为稀疏,这种情况有利于近地点附近插值精度的提高,而损失了远地点附近的插值精度,使得近地点附近和远地点附近插值精度的差异变小.由(11)式可知,随着δ增大,插值基点在近地点附近的密集程度以及在远地点附近的稀疏程度均得到进一步增强,因此δ的取值决定了近地点附近和远地点附近插值精度的差异大小,可通过δ值的合理选取,使近地点附近的插值精度与远地点附近的插值精度相当,此时星历计算误差在轨道上的分布较为均匀,易于满足星历计算的精度要求.

当δ<−1时,情况正好相反,近地点附近的插值精度进一步恶化,远地点附近的插值精度则不必要地提高,δ的取值明显不合理.此外,数值实验表明,δ>1将使得远地点附近的插值精度损失过大,因此本文将δ的取值范围限定为从−1到+1,即δ在闭区间[−1,1]中取值.

采用(1)式和(11)式两种基点划分方式,一个轨道周期含有的插值基点数量大致相同,因此两种方式的计算效率基本相同.以上的分析表明:相比于(1)式,(11)式能够在不影响计算效率的前提下,通过一种合理的非均匀间隔的基点划分,使插值误差在轨道上的分布均匀化,从而在整体上提高了大偏心率轨道的星历计算精度.

2.2 插值方法的选择

不同的插值方法也会对实验结果产生影响,因此本文选择了多种常见插值方法进行比较,一共选择了4种插值方法,分别是拉格朗日插值、牛顿插值、内维尔插值、埃尔米特插值.

拉格朗日插值、牛顿插值、内维尔插值都是多项式插值,这些插值方法通过构造多项式作为函数的近似.函数f(x)的拉格朗日插值多项式[11]:

其中x0,x1,···,xn是基点,lk(x)为拉格朗日基本多项式:

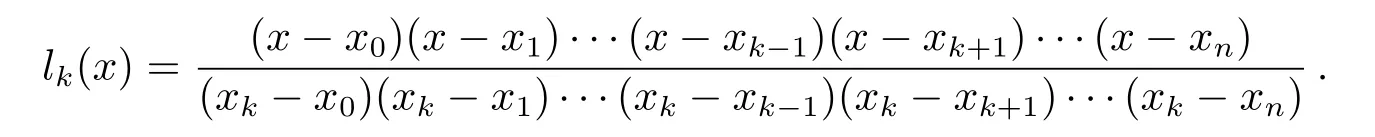
构造函数f(x)的牛顿插值多项式[11]:

其中an(x)为在点x0,x1,···,xn处的m阶差商f[x0,x1,···,xn]:

内维尔插值是一种逐步插值方法,将高阶插值归结为线性插值的重复,即先求相邻两点的一次插值多项式,再两两组合获得2次插值多项式,之后进一步组合成更高阶的插值[11],它满足迭代关系:

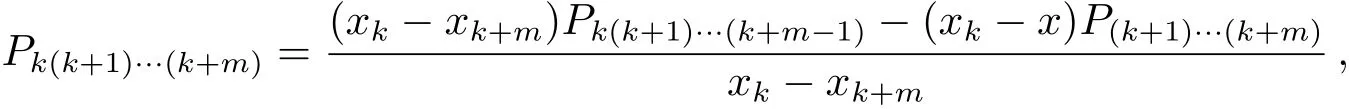
其中Pk(k+1)···(k+m)表示经过xk,xk+1,···,xk+m的m次插值多项式.

与拉格朗日插值不同,埃尔米特插值除了要求插值多项式H2n+1(x)与函数f(x)在基点上的值相等,还要求相应导数值相等,在这里采用1阶导数值相等的形式[12].即满足条件:

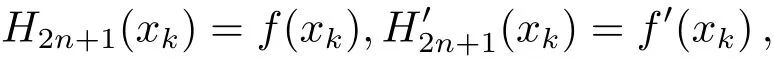
H2n+1(x)可以表示为:

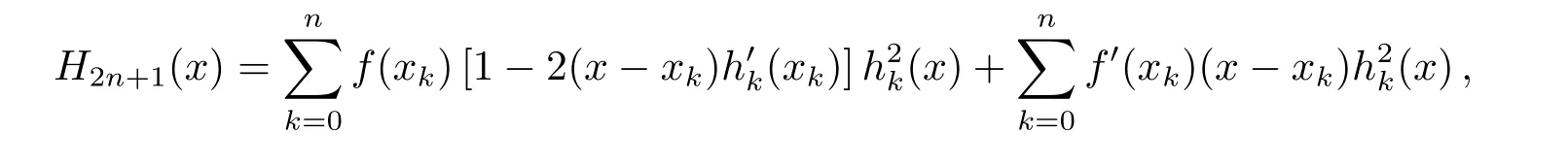
其中

计算中需要的1阶导数可以由简单2体模型给出,也可以由摄动函数计算出.在数值实验中采用摄动函数计算,这样可以保证1阶导数接近真实值,提高插值结果精度.

3 数值实验和分析

δ和N的取值会影响计算效果,δ越大,近地点附近的插值误差越小,而远地点附近的插值误差越大,δ取值过大将会导致远地点附近的插值误差溢出精度范围;N越大,插值精度越高,但此时插值基点数量增多,导致计算效率下降.

δ和N的最佳取值需通过大规模数值实验确定,在以下实验中,我们设定位置量的平均插值精度为10−7(单位为地球赤道半径ae).

考虑空间目标轨道的实际分布状况,采用以下方式选取多组不同偏心率目标轨道用于数值实验,a和e的取值由以下约束条件限定:

即轨道近地点高度保持不变,e的取值从0.0开始一直到0.9,每隔0.05取一个值,a的取值随e的取值由约束条件(12)式计算得到,其他轨道根数的取值不影响问题的本质,在实验中统一取为固定值,具体取值为:i=45◦、Ω =0◦、ω=0◦、M=0◦,其中i为轨道倾角,Ω为升交点赤经,ω为近地点幅角,M为平近点角,根数历元时刻统一取为:t0=58362.0,单位为MJD(Modi fied Julian Day),由此共产生了19组目标轨道根数.

对于每组轨道根数,可由a计算得到P,拟产生星历的密集时刻点ti从t1=t0+P/2开始,每秒1点,至tm=t0+21P/2结束,历经10个轨道周期.

基于每组轨道根数,经转换可得到t0时刻的位置矢量和速度矢量,可作为星历计算的初值.以t0时刻作为第零个插值基点,按前文所述方法构造其余的插值基点.在基点构造过程中,采用RKF8(7)(Runge-Kutta-Felhberg)方法以变步长积分方式产生基点上的星历值,每步积分的截断误差对位置量控制在10−10ae,对速度量控制在10−10ae·d−1.

为方便统计插值误差,需要产生ti上的标准星历值.在本实验中,这些标准星历值由RKF8(7)方法以变步长方式逐点积分得到,积分过程中对局部截断误差的控制精度同上,由于局部截断误差控制精度远高于插值精度要求,因此这些标准星历值可作为衡量插值误差的依据.

对任一星历时刻ti,设内插得到的星历值为⃗ri和˙⃗ri,其上的标准星历值记为和,则位置矢量⃗r和速度矢量˙⃗r的插值误差分别为:

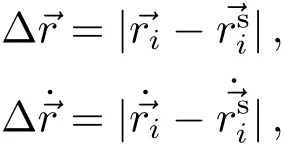
在本文实验中我们仅考虑位置量的插值误差.

3.1 力学模型

前文在方法说明时采用了2体模型,这主要是便于理论推导和说明,并不会对结果产生本质影响.考虑到方法和结果的实用性,在数值实验时还是按照摄动模型进行.本文考虑了以下摄动因素:地球非球形引力、第3体引力(太阳和月球)、太阳辐射压、大气阻力.

由于地球并不是理想均匀球体,它形状不均匀,密度分布不均匀,因此它的非球形引力势可表示[13]为:

其中Me为地球质量,和为归一化的球谐系数,为归一化的勒让德多项式,本文采用了GRIM4-S4引力场模型,引力场阶数取到8×8.

若设⃗R为卫星在地固坐标系中的位置矢量,⃗r为卫星在历元地心天球坐标系中的位置矢量,则相应的地球非球形引力摄动加速度F1为:

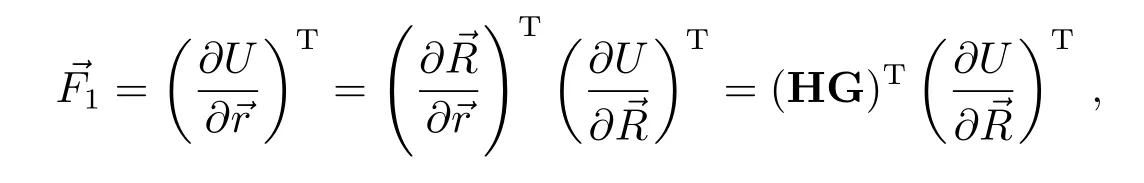
其中,HG矩阵由极移、自转和岁差章动矩阵构成,岁差章动矩阵的相关参数由IAU(International Astronomical Union)2000A岁差章动模型确定,的具体计算见文献[14].

在当前要求的计算精度下,只需考虑作为质点的日、月引力摄动就已足够,它们的摄动加速度可表示为同一形式:

其中m′是日、月质量,是日、月的地心位置矢量.日、月的地心位置可由数值方法或分析方法给出,本文采用了日、月位置分析公式[15].

太阳辐射压的加速度公式为:

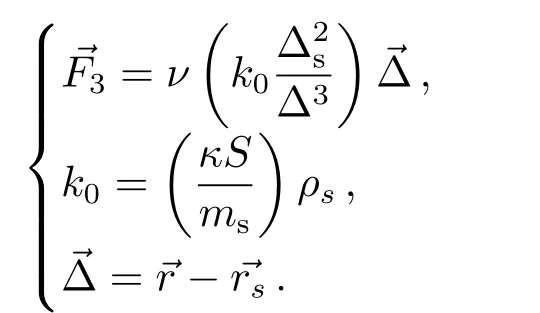
其中,S、ms分别是空间目标的截面积和质量,为太阳的地心位置矢量,k0中的κ=1+η,η是卫星表面反射系数,ρs是距太阳∆s处的光压强度,常取为地球表面处的值,即ρs=4.5605×10−6N·m−2=0.3635×10−12Med−2,对应的∆s=1 au=1.49597870×108km=2.3455×104ae,ν为地影因子,本文采用锥形地影模型,ν由相应的地影函数计算出.

大气阻力摄动加速度采用如下近似表达式:

其中,CD是阻力系数,通常可取为常数,即CD=2.2,⃗v为卫星在历元地心天球坐标系中的速度矢量,⃗va为历元地心天球坐标系中的大气旋转速度矢量,ρ为大气密度,本文采用了DTM94(Drag Temperature Model)大气密度模型[16].

3.2 插值构造方法参数选择

关于δ和N的合理取值,一般有如下问题的提法:在一定的插值精度要求下,对某个δ值,一定存在一个最小的N值Nδ,即Nδ=N(δ),使得δ和Nδ用于星历计算时能够满足插值精度要求,遍历δ取值范围内的所有δ值,求取对应的Nδ值,其中最小的Nδ就是最佳的N取值,其对应的δ也就是最佳的δ取值,此时能够在满足插值精度的前提下,达到最优的计算效率.

在此数值实验中,使用9阶拉格朗日插值方法,选用分别针对不同偏心率的目标轨道进行δ和N的取值实验,先在δ的取值范围内选取δ值,当δ值一定时,选取多个不同的N值进行试算并实时统计位置量的插值精度,最终得到符合精度要求的最小N值Nδ.

图1展示了N与e、δ的关系,可以看到基本上大偏心率对应的最佳δ在0.3附近,而小偏心率则无明显的最佳δ,在区间内都可满足要求,详细实验结果表明δ可取为0.3.

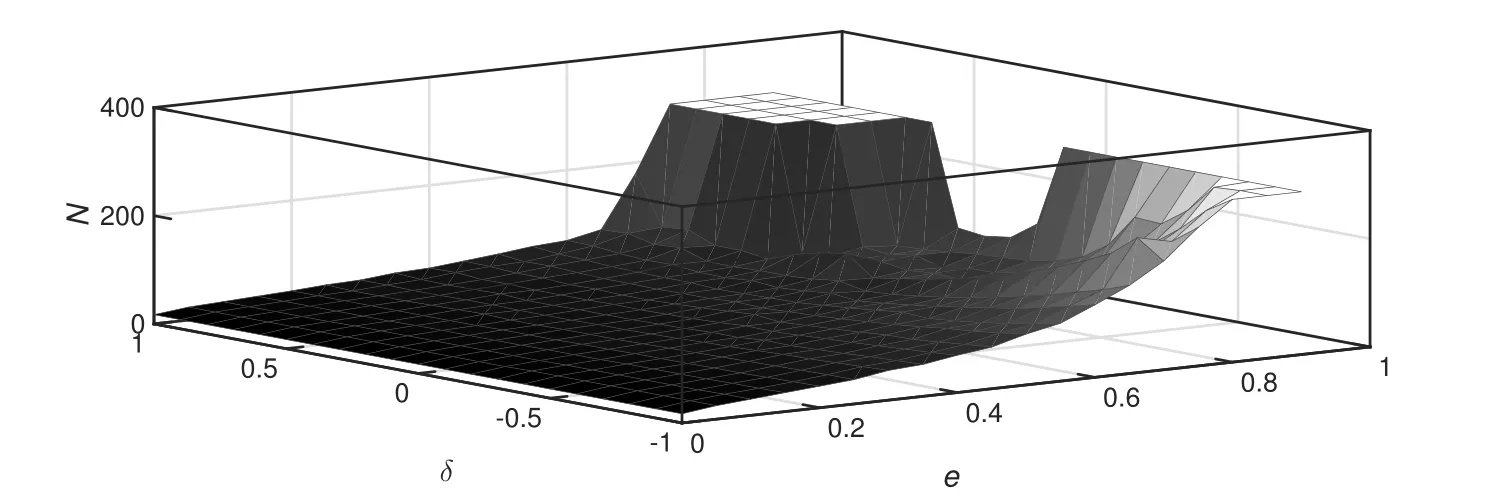
图1 N与e、δ的关系Fig.1 The relationship between N and e,δ

图2和图3展示了不同插值基点划分方式对插值误差分布的影响.此处计算对应轨道根数取为a=10.5ae、i=45◦、Ω =0◦、ω=0◦、M=0、e=0.8、N=80. 图中横坐标M是平近点角,单位是弧度,纵坐标err是位置插值误差,单位是ae,纵坐标erv是速度插值误差,单位是ae·d−1.图2展示了均匀划分的情况,可以看到误差集中出现在2π,即近地点附近,而且位置插值误差最大值接近0.01ae,速度插值误差最大值接近4ae·d−1.图3展示了非均匀划分时的情况,此时δ取0.3,此时误差分布向近地点两边扩散,但位置插值误差最大值不到1×10−7ae,速度插值误差最大值不到3×10−5ae·d−1.可见对插值基点进行非均匀划分,可以使插值误差分布较为均匀,并大为减小最大插值误差.

3.3 最佳插值方法选择

在此数值实验中,基于编目工作的一般精度要求和已有的实算经验,对各插值多项式阶数进行了适当选取,其中拉格朗日插值多项式、牛顿插值多项式和内维尔插值多项式均取为9阶,埃尔米特插值多项式取为7阶.为选出最合适的插值方法,在相同精度要求下,按不同e和不同的插值方法分别计算了对应的δ和N的最佳取值,统计各插值方法在最佳δ和N取值时的右函数计算次数和CPU(Central Processing Unit)计算时间,右函数计算次数越少,CPU计算时间越短,说明计算效率越高,即为最佳插值方法.

图2 均匀基点的插值误差Fig.2 Interpolation error of uniform nodes

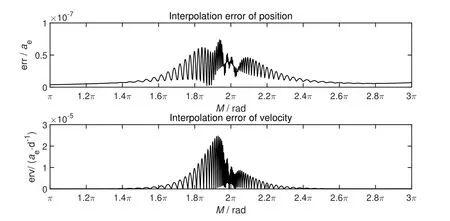
图3 非均匀基点的插值误差Fig.3 Interpolation error of non-uniform nodes

图4和图5展示了不同插值方法对应的右函数计算次数和CPU计算时间,图中,“lgr”表示拉格朗日插值方法,“new”表示牛顿插值方法,“nev”表示内维尔插值,“her”表示埃尔米特插值方法.

从图4可以看出拉格朗日插值、牛顿插值、内维尔插值所需右函数计算次数相同,相应的图像完全重合,而埃尔米特插值所需右函数计算次数较少.

从图5可以看出内维尔插值CPU计算时间最多,埃尔米特插值所需CPU计算时间最少,拉格朗日插值、牛顿插值所需CPU计算时间居中且相差不多,数值实验结果表明埃尔米特插值方法效率最高.

3.4 应用与结果分析

作为本文所提出的积分插值方法的一个应用,在此数值实验中,分别采用逐点积分方法和本文方法对不同偏心率轨道进行星历计算,统计两种方法各自所需的积分右函数计算次数和CPU计算时间.

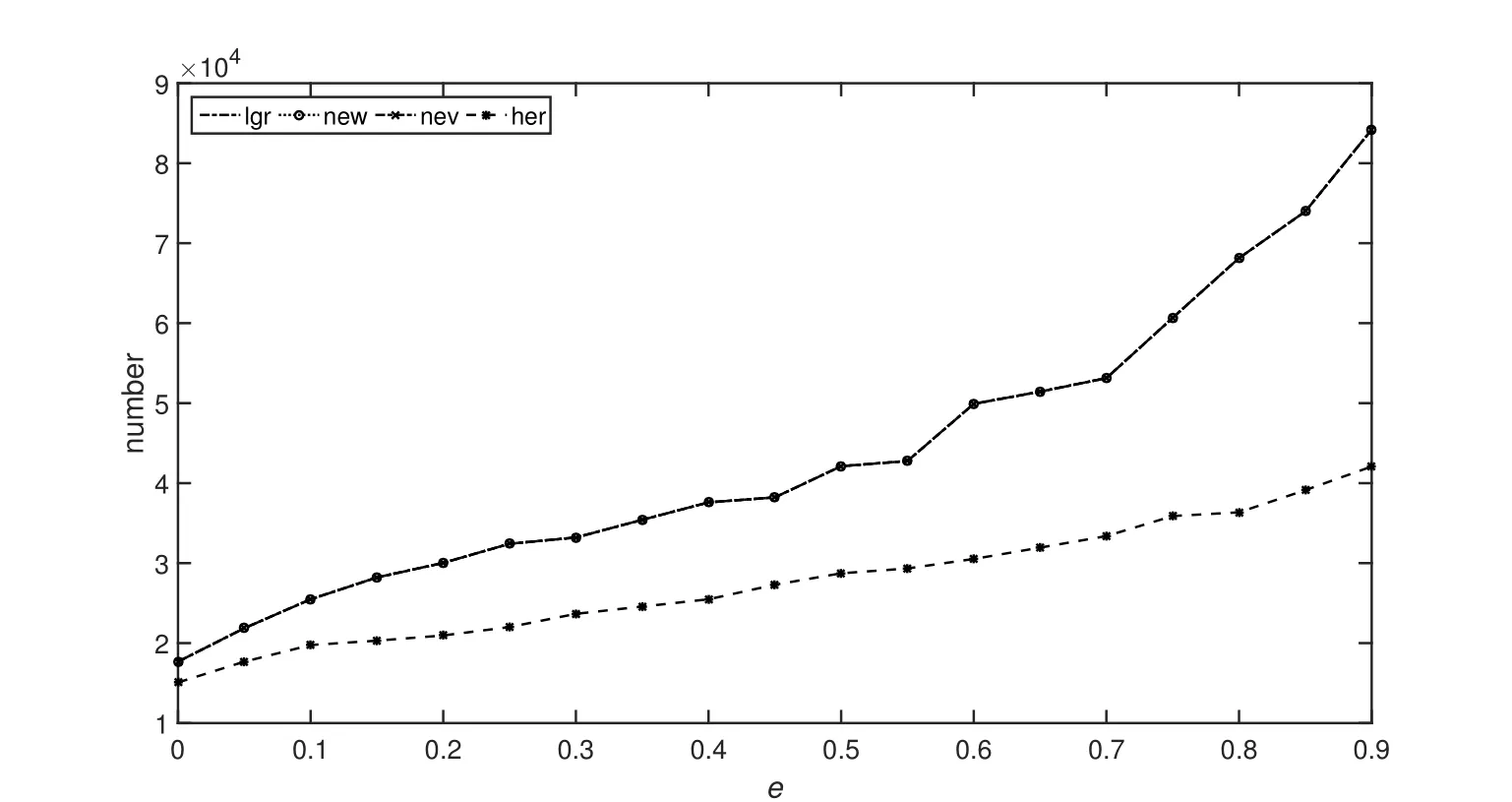
图4 不同插值方法对应的右函数计算次数Fig.4 Number of right function calculation corresponding to di ff erent interpolation methods

图5 不同插值方法对应的CPU计算时间Fig.5 CPU computing time corresponding to di ff erent interpolation methods

在逐点积分法中,采用RKF8(7)方法以变步长方式积分产生密集星历点ti上的星历值,局部截断误差对位置量控制在10−8ae,对速度量控制在10−7ae·d−1,考虑局部截断误差的累积效应,采用逐点积分法在本算例中实际产生的位置误差大致为10−7ae量级,速度误差大致为10−6ae·d−1量级.

在积分插值法中,仍采用RKF8(7)方法以变步长方式积分产生插值基点上的星历值,局部截断误差对位置量控制在10−10ae,对速度量控制在10−10ae·d−1,密集星历点ti上的星历值采用7阶埃尔米特插值得到,构造插值基点时选取δ=0.3,N值由数值实验得到,对不同偏心率轨道有不同取值,以确保位置量插值误差为10−7ae量级,速度量插值误差为10−6ae·d−1量级,使得积分插值方法与逐点积分法具有大致相同的星历计算精度.

用于星历计算的目标轨道根数与前文相同,对于每组轨道根数,密集星历点ti从t1=t0+P/2开始,每秒1点,至tm=t0+3P/2结束,历经一个轨道周期.

表1展示了逐点积分法和积分插值法的右函数计算次数和CPU计算时间对比,表格中,num表示右函数计算次数、point-by-point integration下的cpu-time表示逐点积分法所需的总共计算时间、integration interpolation下的cpu-time-1表示积分插值法中积分插值基点所用计算时间、cpu-time-2表示积分插值法中插值所用计算时间、cpu-time-3表示积分插值法总共的计算时间.从表1各项结果可知,积分插值法因插值基点在轨道上的分布较为稀疏,相比于逐点积分法,尽管局部截断误差控制精度较高,但其所需的积分右函数计算次数大大减少,积分计算时间也随之大大减少,积分插值法所需的计算时间主要为插值计算时间,由于插值计算是一个简单的代数运算,具有极高的计算效率,因此积分插值法的总体计算时间相比于逐点积分法大大减少,在本算例中两种方法的计算效率相差接近100倍.

表1 逐点积分法和积分插值法计算效率对比Table 1 Comparison of computation efficiency between point-by-point integration method and integration interpolation method

4 结论

本文提出了一种适用于大椭率轨道的高效精密密集星历计算方法,即联合使用非均匀基点构造方法和插值方法,本文研究工作具有以下特点:

(1)针对大偏心率轨道计算,提出了一种以时间变换方法确定插值基点并内插得到密集星历的新方法,可显著提高计算效率和精度;

(2)基于大规模数值实验,给出了对应于不同轨道偏心率和多种插值多项式的时间变换参数δ的最佳适配值,并确定δ=0.3为最佳的普适数值;

(3)研究了多种插值方法,在时间变换参数δ最佳适配的条件下,比较了它们的插值精度和计算效率,并确定埃尔米特插值是一种较好的方法;

(4)通过实际计算对比了本文所提处理方法与逐点积分法的计算效率,结果表明本文所提处理方法的计算效率大大提高,对于提升编目处理的时效性具有重要的应用价值.

本文所提出的方法虽然源自于解决编目处理的时效问题,但也可拓展到其他应用领域,其中一个最重要的方面就是广播星历预报,它是各类空间应用的基础.由于本文方法具有很强的通用性,并不局限于某一特定的轨道类型,如导航星具有的小偏心率近圆轨道,因此该方法相对于目前普遍使用的导航星广播星历计算方法具有更广阔的应用前景.此外,该方法也可在自然天体的历表编制工作中得到应用,如彗星历表编制等.