亚纯函数的不动点

郑耒芳

(广州民航职业技术学院 人文社科学院，广东 广州 510403)

一、引言及主要结果

设f(z)是复平面上的亚纯函数，对任意的z∈，如果f(z)=z则称z为f(z)的不动点。庄圻泰、杨重骏[1]系统研究了亚纯函数的不动点。本文将利用Nevanlinna理论研究亚纯函数及其导函数乘积的不动点。为此，假设读者熟知Nevanlinna理论的标准记号，如等(可见Haymann[2],杨乐[3]，仪洪勋、杨重骏[4]，郑建华[5]等)。此外，用σ(f)表示

f(z)的级，τ(f)表示f(z)的不动点的收敛指数[6]，δ(a,f)表示f(z)的a∈∪{∞}值点的Nevanlinna亏量，即

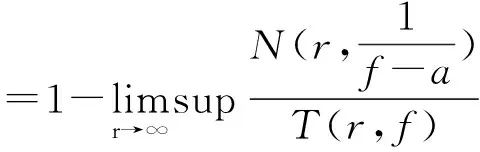
1960年左右，Baker[7]证明：对全平面上的超越整函数f，如果存在a∈使得δ(a,f)>0则函数

f有一阶不动点。 1993年, Lahiri[8]部分推广了Baker的结果，得到如下结果。

定理A设f是全平面上的超越亚纯函数，如果存在a∈使得δ(a,f)>0且δ(∞,f)=1。则f有无穷多个不动点。

吴昭君[9]推广了定理A，得到

定理B 设f是全平面上的超越亚纯函数，如果存在a∈使得δ(a,f)>0且δ(∞,f)=1。则对任意的正整数k，f和f(k)有无穷多个不动点, 且τ(f)=σ(f)=τ(f(k))。

本文将研究亚纯函数f及其导函数f(k)的乘积ff(k)的不动点，证明如下定理。

定理1.1设f是全平面上的超越亚纯函数，如果δ(0,f)>0且δ(∞,f)=1，则对任意的正整数k，ff(k)有无穷多个不动点,且τ(ff(k))=σ(f)。

定理1.2设f是全平面上的超越亚纯函数，如果δ(0,f)=δ(∞,f)=1，则对任意的正整数k，ff(k)有无穷多个不动点,且

当f(z)是无穷级亚纯函数时，可能需要除去一个线测度有穷的集合。

二、定理的证明

定理的证明需要用到如下引理。

引理2.1(对数导数引理)设f(z)是全平面上的超越亚纯函数，则当f(z)是有穷级时

S(r,f)=o(T(r,f))(r→∞),

当f(z)是无穷级时

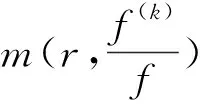
=o(T(r,f))(r→∞,r∉E),

其中k为任意正整数，E是一个有穷线测度的集合。

引理2.2[4]设f(z)是开平面上的非常数亚纯函数，P(f)=a0fn+a1fn-1+…+an，其中a0(≢0)，a1,…，an均为f的小函数，则T(r,P(f))=nT(r,f)+S(r,f)。

引理2.3设f(z)是开平面上的非常数亚纯函数，且δ(0,f)>0，则对任意的正整数k，ff(k)是超越亚纯函数。

证明因为f是超越亚纯函数，且δ(0,f)>0，则ff(k)是超越亚纯函数。如若不然，则存在有理数R(z)，使得R(z)ff(k)≡1。因此，结合引理2.1可得

由Nevanlinna第一基本定理和引理2.2，有

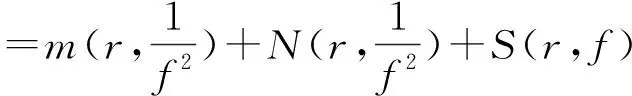
这与δ(0,f)>0矛盾。因此ff(k)是超越亚纯函数。证毕。

引理2.4 设f(z)是开平面上的非常数亚纯函数，且δ(o,f)>0，则对任意的正整数k，有

(2.1)

证明因为f是超越亚纯函数，且δ(0,f)>0，由引理2.3知ff(k)是超越亚纯函数。注意到

T(r,ff(k))=m(r,ff(k))+N(r,ff(k))

结合引理2.1可得

T(r,ff(k))≤2T(r,f)+kN(r,f)+S(r,f)。

(2.2)

因此

S(r,ff(k))=S(r,f)。

(2.3)

因为ff(k)是超越的，所以(ff(k)-z)"=f"f(k)

+2f'f(k+1)+ff(k+2)≢0。令

结合引理2.1知

由Nevanlinna第一基本定理和引理2.2可知，

因此

(2.4)

由Nevanlinna第一基本定理并结合引理2.1及(2.3)式，有

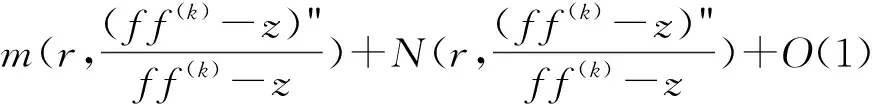
因此

(2.5)

由式(2.4),(2.5)可得

(2.6)

证毕。

下面给出定理1.1和定理1.2的证明。

定理1.1的证明因为δ(∞,f)=1，δ(0,f)>0，则存在某个正数θ<1，使得对任意充分大的r，有

(2.7)

且N(r,f)=o(T(r,f))

(2.8)

由引理2.4并结合(2.7)，(2.8)可得

因为f是超越的，因此ff(k)有无穷多个不动点，且

σ(ff(k))≥τ(ff(k))≥σ(f)，

另一方面，由(2.2)式可得σ(ff(k))≤σ(f)。故有τ(ff(k))=σ(f)。证毕。

定理1.2的证明因为δ(∞,f)=δ(0,f)=1。则有

(2.9)

结合式(2.1), (2.2), (2.9)可得

T(r,ff(k))≤2T(r,f)+kN(r,f)+S(r,f)

≤2T(r,f)+S(r,f)

≤T(r,ff(k))+S(r,f)。

由引理2.3知ff(k)是超越的，因此ff(k)有无穷多个不动点,且

由引理2.1，当f(z)是无限级亚纯函数时,上述取极限的过程可能需要除去一个线测度有穷的集合。定理1.2得证。