基于伪损伤等效的汽车动力传动系统试验场关联

张志超,董强强,杨建森,郝鹏祥

(1.国家知识产权局专利局专利审查协作天津中心，天津 300304； 2.中汽研(天津)汽车工程研究院有限公司，天津 300399)

汽车动力传动系统是实现汽车运动功能的关键部分，其耐久性能直接影响汽车的使用寿命，以及驾驶员和乘客的安全。汽车动力传动系统不仅要承受路面不平而产生的冲击，而且要受到发动机输入扭矩的影响[1-2]。因此，动力传动系统的耐久性能分析被各汽车厂商深入研究，部分汽车主机厂商甚至单独制定了动力传动系统的耐久规范。由于地理位置、开发周期、试验成本、试验场资源不足等因素的限制，部分厂商需要将一个试验场的动力传动系统耐久规范转移至另一个试验场，即动力传动系统的试验场关联。目前，相关学者在基于用户关联的动力传动系统台架试验载荷谱编制、试验规范编制方面做了大量研究[3-5]，但动力传动系统试验场关联的研究较少且关联方法有局限性。基于动力传动系统宏观参数(车速分布、挡位使用时间、发动机转速等)的对标关联未进行动力传动系统疲劳损伤的验证，较难保证结构耐久程序关联的可靠性；基于动力传动系统做功输出能量的试验场关联方案关注的是动力传动系统扭矩的等效关联，但未考虑零部件材料属性对疲劳损伤的影响。

本研究以某型号的国产SUV作为试验样车进行路谱采集，以Miner线性累积损伤理论为理论基础，通过计算不同工况、不同挡位下左右传动轴扭矩的伪损伤值来构造损伤矩阵及优化函数，采用粒子群优化算法实现动力传动系统试验场关联计算求解，为汽车动力传动系统试验场关联提供了一种新方法。

1 动力传动系统试验场关联理论与原理

1.1 Miner线性累积损伤理论

疲劳指材料内部某点或某些点在反复循环载荷作用下产生的局部永久性结构变化，且在经历足够多的循环加载后形成裂纹并最终完全断裂[6]。汽车金属零部件的损坏主要是由累积疲劳损伤所造成的[7]。在汽车驾驶过程中，虽然零部件受到的最大应力没有超过其材料的强度极限，但由S-N曲线可知，每次在一定范围内波动的应力幅值均会对零部件造成一些损伤，累积损伤积累到一定程度，零部件就会因疲劳产生破坏。

由于Miner线性累积损伤理论的疲劳寿命评估与试验结果在多数情况下有很高的吻合度，故被广泛应用[8]。车辆在行驶过程中，传动系统各部件受到随时间变化的随机载荷作用而产生动态循环应力，由Miner 线性累积损伤理论可知部件的总损伤如下[9-10]：

(1)

式中：D为疲劳累积损伤；K为载荷等级；ni为第i级载荷下的实际载荷循环次数；(Nf)i为第i级载荷下的疲劳寿命。当D=1时，承载结构出现裂纹，最终导致疲劳破坏。

1.2 动力传动系统试验场关联原理

图1 动力传动系统试验场关联矩阵Fig.1 Correlation matrix of powertrain and proving ground

在汽车动力传动系统中，各传动轴主要受到扭矩的作用而产生疲劳破坏。因此，以驱动轴左、右两半轴扭矩为测量对象，根据汽车各挡位信号将两半轴扭矩数据按挡位分解，基于各挡位的两半轴伪损伤等效原则，建立试验场A(关联试验场)与试验场B(目标程序试验场)的动力传动系统试验场关联，见图1。如图1所示，将试验场B各挡位的两半轴伪损伤和作为目标损伤，将试验场A各挡位的两半轴伪损伤作为系数矩阵，通过求解循环次数建立两试验场的关联关系，完成两试验场的动力传动系统关联。

2 路谱采集与数据处理

根据上述传动系统试验场关联原理，将左、右半轴扭矩和挡位信号作为采集通道。对于试验场B，按照某目标程序确定试验场B的采集工况，目标程序工况如表1所示；试验场A的工况选取直接影响关联结果，所以可通过分析试验场B目标程序的采集工况选取试验场A的部分工况，选取的试验场A的采集工况如表2所示。

表1 目标程序工况及循环列表Tab.1 Target specification events and cycle list

表2 试验场A选取工况Tab.2 Selected events of proving ground A

通过应变片测量两半轴的扭矩，通过挡位测量装置获取挡位信号，图2为半轴扭矩传感器安装图。图3为高速外循环工况采集的数据，其中通道1(Ch1)为左半轴扭矩信号，通道2(Ch2)为右半轴扭矩信号，通道19(Ch19)为GPS车速信号。采集信号经过检查、截取、毛刺去除、按挡位信息分解、伪损伤值计算等处理，得到传动系统关联计算所需的各工况、各挡位下的数据。在伪损伤值计算中，由于要考虑材料属性，故需要设置材料的S-N曲线参数。

图2 半轴传感器安装图Fig.2 Installation of half shaft sensor

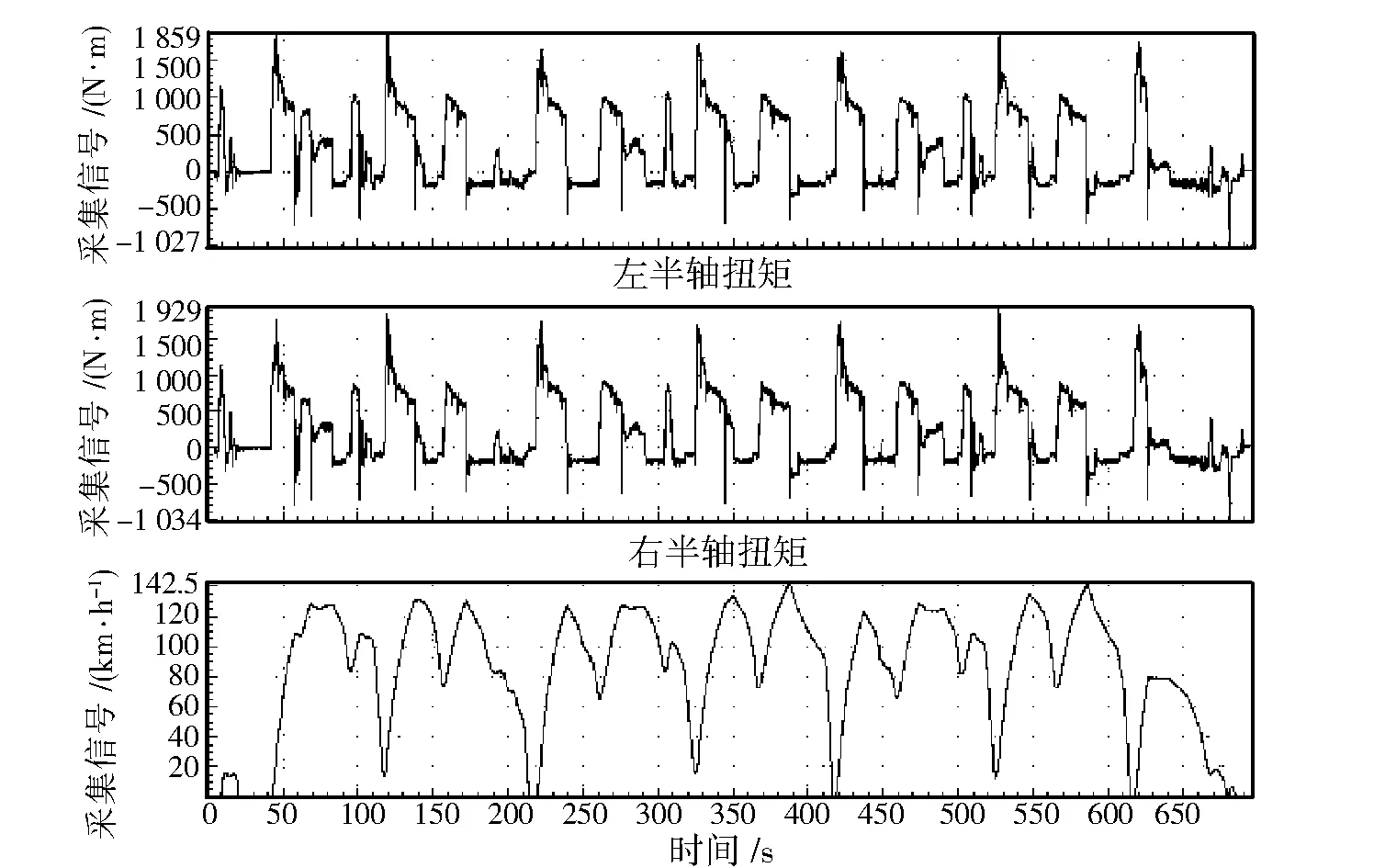
图3 信号采集示意图Fig.3 Diagram of acquisition signal

3 基于粒子群算法的动力传动系统试验场关联计算

3.1 动力传动系统试验场关联函数的构建

基于图1的关联原理，利用采集的数据构建关联方程。以目标试验场B各工况、各挡位下的两半轴扭矩伪损伤和为关联目标，以试验场A各选取工况、各挡位下的两半轴扭矩伪损伤为关联通道并构成关联矩阵，以试验场A各选取工况的循环次数为求解变量，最终得到关联方程如下：

[Aij]·[kj1]=[Bi1],

(2)

式中：Aij为试验场A的关联矩阵，表示各通道、各工况损失值；kj1为试验场A各工况的循环次数；Bi1为目标试验场的关联目标。

在动力传动系统试验场关联中，由于目标试验场工况较多，上述关联方程的解往往不唯一。同时，由于关联方程中求解变量个数较多，通过方程求解获取试验场A各工况的循环次数较为困难，为便于动力传动系统试验场关联的求解，将关联方程求解问题转化为优化求解问题，其数学表达式如下：

(3)

将Δ作为优化函数，将试验场A各工况的循环次数kj1作为优化变量，采用优化算法对式(3)进行优化求解，可得到关联试验场A各选取工况的循环次数。

3.2 基于粒子群算法的动力传动系统试验场关联的实现

粒子群算法是一种种群智能优化算法[11-12]，其通过迭代寻找最优解，具有易实现、精度高、收敛快等优点[13]。在动力传动系统试验场关联优化求解中，采用MATLAB软件实现求解算法的构建，将Δ作为适应度函数，将试验场A各选取工况的循环次数kj1作为粒子的位置，设置约束条件，求解流程如图4所示。优化求解的迭代收敛曲线如图5所示。

利用采集、处理得到的试验数据，通过算法优化求解并根据经验优化得到的试验场A各工况的循环次数，如表3所示。

由图5可以看出，计算收敛且迭代次数较少，收敛时的适应度值相对较小，验证了粒子群算法用于动力传动系统试验场关联求解的可行性及有效性。考虑到试验场A耐久规范的可执行性(行驶路线规划合理)，试验场A的各工况循环次数需要在算法优化求解的基础上再根据工程经验适当优化。上述过程实现了基于粒子群算法的传动系统试验场关联计算，获取了试验场A选取工况的循环次数。

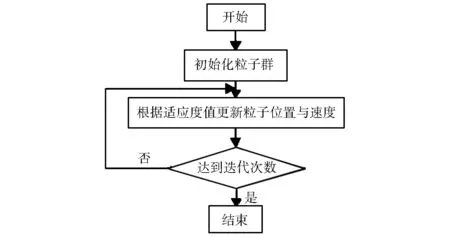
图4 粒子群算法求解流程Fig.4 Flowchart of particle swarm optimization

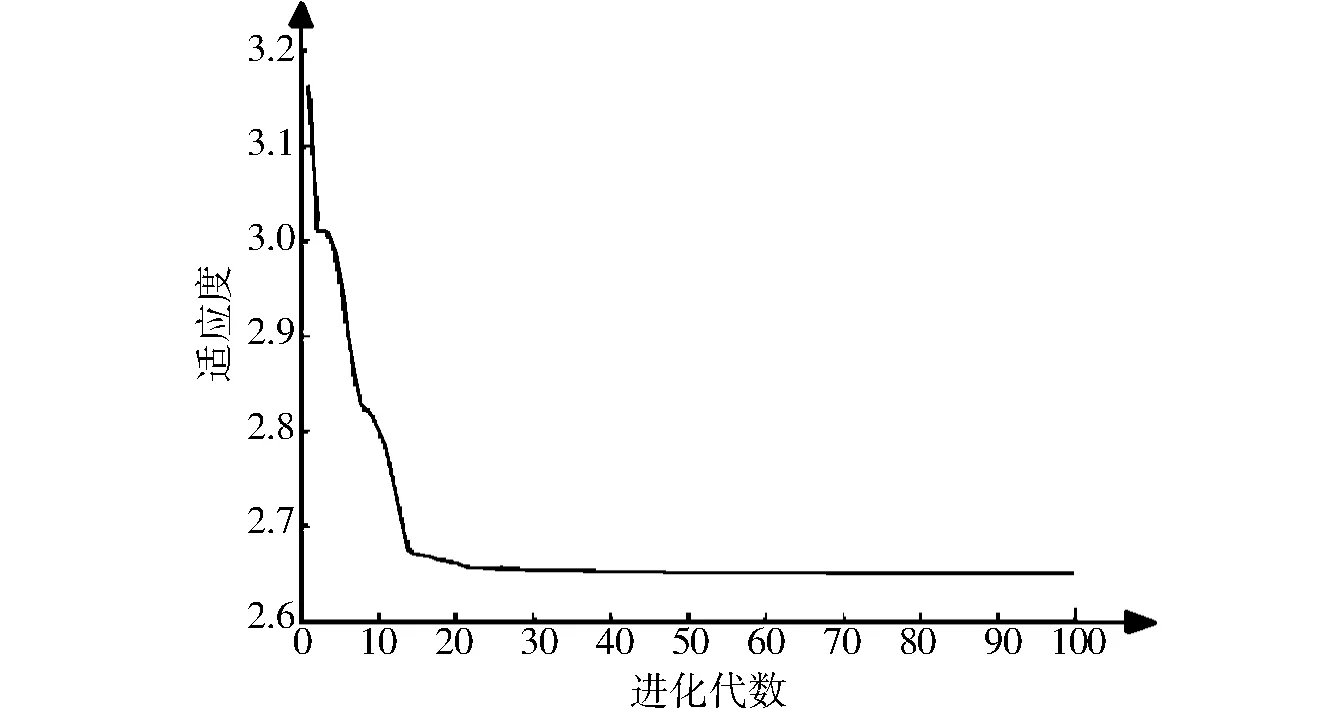
图5 迭代收敛曲线Fig.5 Iterative convergence curve

表3 试验场A选取工况及循环次数Tab.3 Events and cycles of proving ground A

4 关联结果验证

4.1 伪损伤对比验证

伪损伤对比即两试验场程序的相对损伤比。在动力传动系统试验场关联中，两试验场程序的伪损伤对比是关联结果评价最重要且最直接的判断依据。试验场A关联计算程序与试验场B目标程序的伪损伤对比结果见图6。

如图6所示，各关联通道的相对损伤比均落在factor=2和factor=0.5的区域中，且大部分关联通道的相对损伤比在1.0附近。在动力传动系统试验场关联中，两试验场程序相对损伤比的理想值为1.0。但是，由于两试验场工况的差异性、优化函数的复杂性，两试验场程序的相对损伤比完全等于1.0是较难实现的。

4.2 挡位使用参数对比验证

将各挡位下的左、右半轴扭矩的伪损伤作为关联通道，保证了变速器各挡位传动轴的关联效果，但并不能体现出两试验场程序在挡位变换上的对比。在变速器中，挡位变换是通过换挡拨叉实现的，但换挡拨叉受力测量的实现较为复杂。因此，将两试验场规范的换挡次数进行统计对比，间接评估了两试验场规范对换挡拨叉疲劳耐久的考核程度，挡位使用参数对比验证是对关联规范操作的等效校核。

关联试验场与目标试验场规范的换挡统计对比(基于采集获取的挡位信号)见图7。从各挡位换挡次数对比看，两程序换挡次数最大差距为5挡，相差10.38%，在可接受范围。

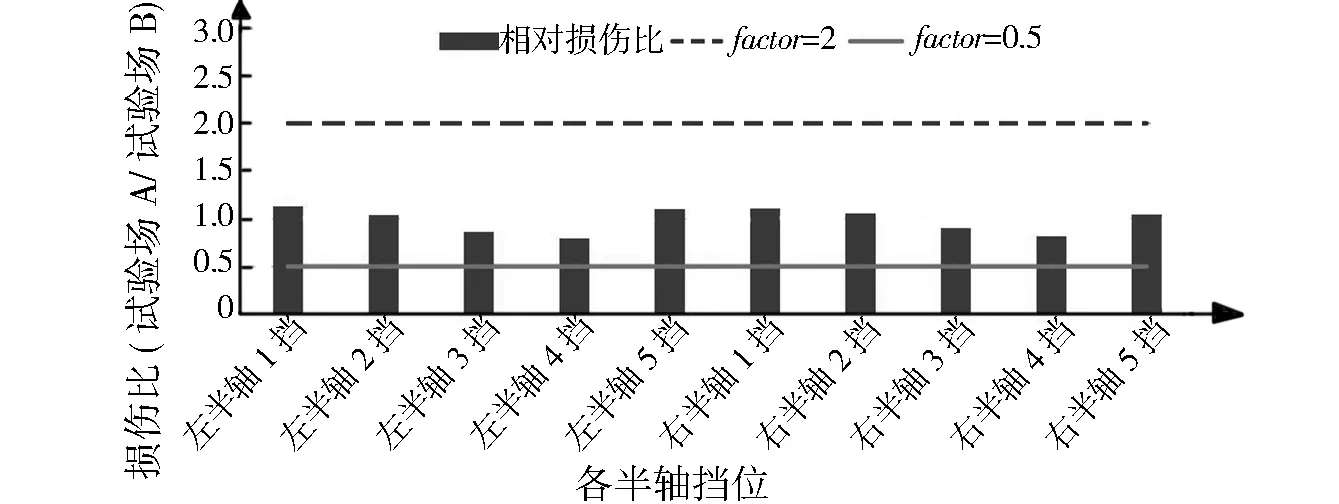
图6 两试验场程序伪损伤对比Fig.6 Pseudo damage comparison of the two proving ground specifications

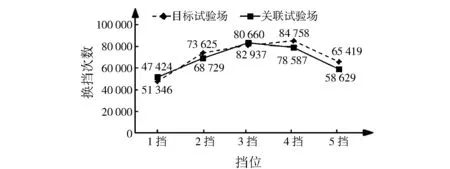
图7 两程序换挡统计对比Fig.7 Comparison shift times of the two specifications

5 结语

本研究提出了以伪损伤等效为原则，以各挡位下左、右半轴扭矩为关联通道的动力传动系统试验场关联方法，为汽车动力传动系统试验场关联提供了新方法，证明了构造关联矩阵、优化函数并采用粒子群算法进行动力传动系统试验场关联较为有效。