聚焦转化 关注本质——《平行四边形的面积》教学

林志辉 林 迪

【教学内容】

人教版五年级上册第87、88 页。

【教学过程】

一、前测唤醒，初感转化

师：他们是怎么想的？

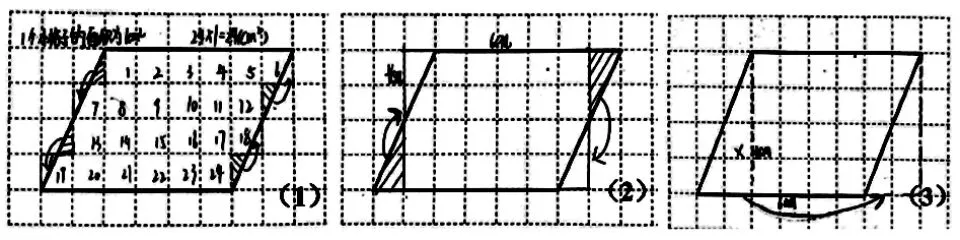
生：第一幅是数格子，第二幅和第三幅都是切完拼成一个长方形。

师：“4×6=24”是什么意思？

生：4 是转化后长方形的宽，6 是转化后长方形的长，4 乘6 是转化后长方形的面积，也是平行四边形的面积。

二、转化归纳，得出公式

1.转化猜想。

师：为什么通过割补的方法求面积都是把平行四边形转化为长方形？

生：因为已经学习了长方形的面积计算公式，把平行四边形转化为长方形，就可以求出平行四边形的面积了。

师：是不是所有的平行四边形都能转化为长方形求面积？（学生交流）

2.活动验证。

师：在方格纸上画一个平行四边形，请同伴转化为长方形求面积。

生1：我画的平行四边形底是6 厘米，高是2 厘米，转化成长是6 厘米，宽是2 厘米的长方形，面积是12 平方厘米。（如图1）

生2：我画的平行四边形底是2 厘米，高是4 厘米，转化成长是4 厘米，宽是2 厘米的长方形，面积是8 平方厘米。（如图2）

3.“斜而长”转化。

师：像图1 和图2 这样的平行四边形，同学们都成功将它转化为长方形。像图3 这样的又斜又长的平行四边形，也可以吗？

图1

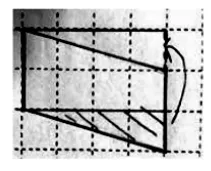
图2

图3

师：为什么这样转化不行？（图4）

生：这样转化，虽然能转化成长方形，却不能直接计算面积。应该分开多割几次，再移过来。

师：你说的是这个意思吗？（课件演示，如图5）

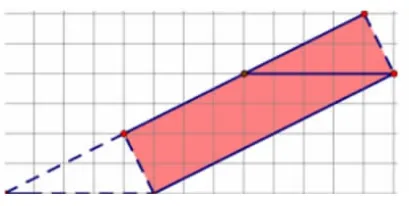
图4

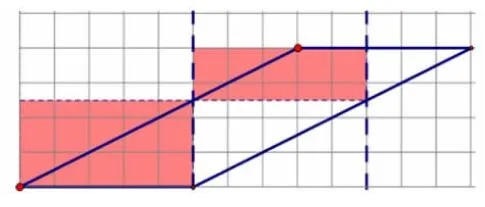
图5

师：那像这样的平行四边形呢？（图6）

生：可以多次分割平移，转化为面积为30 平方厘米的长方形。（教师课件演示）

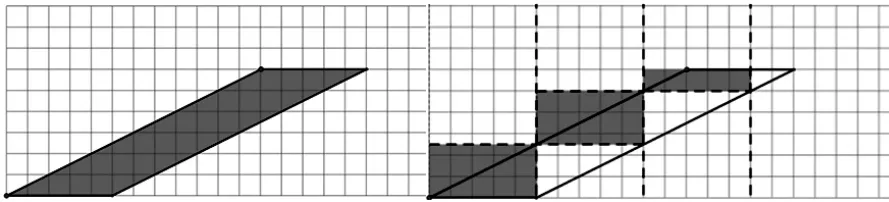
图6

4.沟通联系，归纳公式。

师：转化后的长方形和原来的平行四边形有什么联系？

生：平行四边形的底是长方形的长，平行四边形的高是长方形的宽，平行四边形的面积=长方形的面积，因为长方形的面积=长×宽，所以平行四边形的面积=底×高。

三、练习转化，提升理解

师：请口答下列平行四边形的面积。

生：最后一个的面积求不出来，因为10 厘米不是12 厘米对应的高。

师：为什么不是对应的高就不能求它的面积呢？

生：这个图形不能通过剪拼转化成“底12 厘米、高10 厘米”的长方形，所以不能这样求它的面积。

（教师添加条件，出示12 厘米对应的高8 厘米，引导学生再次求平行四边形的面积，并提问求10 厘米对应的底是多少厘米？课件演示剪拼过程）

四、辨析转化，强化认知

1.引冲突，直面误区。

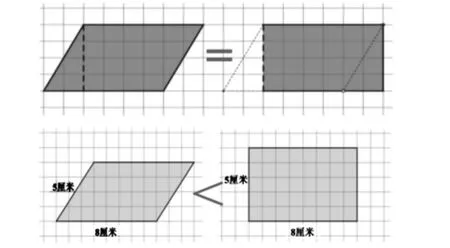
师：平行四边形是易变形的，把平行四边形拉成一个长方形，长方形面积是40 平方厘米（长8 厘米，宽5 厘米），所以原来的平行四边形的面积也是40平方厘米吗？

生：我同意，因为平行四边形拉成长方形，所以面积一样。

生：我不同意，虽然平行四边形的底和长方形的长相同，但是平行四边形的高和长方形的宽不同，所以面积不一样。

2.给方格，深化认知。

师：现在你怎么想的？（课件出示方格图）

生：长方形的面积是40 平方厘米，平行四边形的面积=底×高=8×4=32（平方厘米）。

生：将右边多出来的三角形平移到左边，平行四边形的面积比长方形的面积少一行，少了8 平方厘米。

3.对比转化。

师：都是转化成长方形，刚才的剪拼转化是不变的，现在拉伸转化为什么就不可以了？

生：因为这样拉动过程中，底没有变，高一直在变化，所以平行四边形的面积也一直在变。

生：拉动平行四边形时，高变大，面积就变大，高变小，面积就变小。当平行四边形的高等于长方形的宽时，高最大，平行四边形的面积最大。

师：通过剪拼割补的方法，平行四边形的面积等于长方形的面积，是等积转化。通过拉伸变形成长方形，平行四边形的面积小于长方形的面积，面积变了。

五、等积转化，拓展延伸

1.画等积图形。

师：面积为24 平方厘米的平行四边形还有哪些？请在方格纸上画出来。

2.展示作品。

层次一：等底等高的作品。

师：这些图形有什么共同点？

生：虽然形状不一样，但底和高都相等，面积也相等。

层次二：展示不同底不同高但等积的学生作品。

师：这些平行四边形的面积也都是24 平方厘米，它们有什么特点？

生：都是24 平方厘米，底越大，高越小；底越小，高越大。

3.课件小结。

师：看来只要等底等高，面积总不会变。

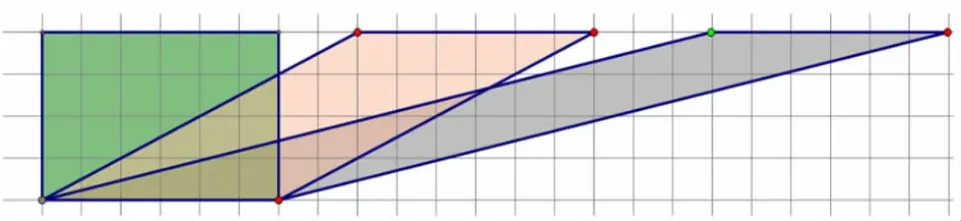
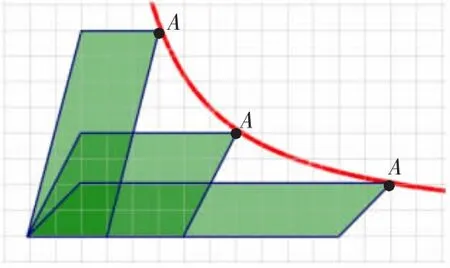
师：请想象，在等积的平行四边形变化过程中，点A 留下的轨迹是什么样的？

（学生想象后，教师课件演示，如图所示）