透明质酸发酵液中还原糖含量的快速估测方法

宋磊，刘苗苗，郭燕风，王宜磊*

1. 菏泽学院农业与生物工程学院（菏泽 274000）；2. 山东丹红制药有限公司（菏泽 274000）

透明质酸（HA）是一种高分子酸性黏多糖，有独特的流变学特性、黏弹性、保湿性及良好的生物相容性，被广泛应用于食品、化妆品、医学等领域[1-5]。微生物发酵法生产透明质酸周期短，环境友好，产量高，是目前最主要生产方法[6-9]。葡萄糖作为发酵生产的唯一碳源，除少量用于菌体代谢增殖外，主要作为底物用于透明质酸的合成，是对发酵过程控制及判定发酵终止时间的重要参数[10-11]。透明质酸发酵液中还原糖含量的测定多采用3, 5-二硝基水杨酸（DNS）比色法[12-14]，方法操作繁琐、耗时长、人为误差大，不能实时监测发酵液中还原糖含量。但透明质酸发酵生产周期短，发酵液各参数变化速度快，尤其在发酵衰亡期，菌体自溶裂解后释放大量透明质酸酶，使透明质酸快速降解，极大地影响透明质酸生产收率及后

续分离与纯化。因此快速估测出透明质酸发酵液中还原糖含量对生产实践有很重要的指导意义。查阅国内外相关文献，发酵工业生产过程中还原糖含量的测定常采用传统的手工滴定法或比色法[15]，鲜见有对发酵液中还原糖含量与其他发酵过程参数相偶联，通过快速检测其他过程参数而快速估测还原糖含量的相关报道。陈莉等[16]提出基于BP神经网络快速估测发酵液中羊肚菌胞外多糖的含量，刘静等[17]通过测定水溶液中浊度快速估测出水中壳聚糖含量，均取得有益的研究经验。结合工厂生产实践，通过对透明质酸发酵过程中发酵液中还原糖含量与其他几个重要参数的相关性及变化规律分析，构建数学模型，以期能达到快速估测出发酵液中还原糖含量的目的。

1 材料与方法

1.1 材料、试剂与仪器

发酵液（山东某生物工程公司）。

咔唑、氢氧化钠、亚硫酸钠、3, 5-二硝基水杨酸、酒石酸钾钠、四硼酸钠、结晶酚（上海麦克林生化科技有限公司）；硫酸、氢氧化钠（天津市永大化学试剂有限公司）；葡萄糖醛酸、葡萄糖标准品（国药集团化学试剂有限公司）。

PL203/01电子分析天平（梅特勒-托利多仪器（上海）有限公司）；DV2TRV旋转黏度计（美国博勒飞（广州）有限公司）；WGZ-200浊度仪（上海昕瑞仪器仪表有限公司）；HK338电导率仪（北京华科仪科技有限公司）；UV5800分光光度计（上海元析仪器有限公司）；H1650离心机（湖南湘仪实验室仪器开发有限公司）；DZF6090真空干燥箱（上海皓庄仪器有限公司）。

1.2 试验方法

1.2.1 发酵液取样

透明质酸发酵周期短，发酵过程中各参数变化快。选定从发酵开始，间隔2 h取样；取2019030901、2019031503、2019040201这3个发酵批次同一发酵时间节点发酵液，检测其中还原糖含量、透明质酸含量、菌体量、浊度、黏度、电导率。

1.2.2 发酵液中菌体、透明质酸、还原糖含量变化曲线

对3个批次同一时间节点测得菌体、透明质酸、还原糖含量取平均值，绘制曲线。

1.2.3 还原糖含量与发酵液中各参数相关性分析

对3个批次同一时间节点测得还原糖含量、透明质酸含量、菌体量、浊度、黏度、电导率取平均值，绘制发酵液中还原糖含量与其他各参数相关性散点图，并根据SPSS 19.0软件分析结果，考察其相关性。

1.2.4 构建数学模型

筛选出与发酵液中还原糖含量变化规律相关显著性参数，利用软件构建一元线性、二次项曲线、BP神经网络3种数学模型，用于预测未知发酵液中还原糖含量。

1.2.5 3种数学模型预测效果比较

对2019060401、2019060503两个批次随机13个发酵液样品中还原糖含量及与其相关性显著参数的含量进行测定；利用一元线性回归、二次项曲线回归分析及BP神经网络3种数据处理方法获得数学模型对发酵液中还原糖含量进行估测；将实测值与模型估测值进行对比，依据试验样本方差作为3种模型的评价指标，用于检验模型的准确性。方差计算如式（1）所示。

式中：S2为方差；Y1为数学模型计算值；Y2为试验测得实测值。

1.2.6 发酵过程中各参数测定方法

发酵液中还原糖的测定参考文献[12-14]。称取6.3 g 3, 5-二硝基水杨酸（DNS）溶于少量蒸馏水中，加入262 mL 2 mol/L氢氧化钠溶液，加入185 g酒石酸钠钾、5 g结晶酚、5 g亚硫酸钠，摇匀，冷却后定容至1 000 mL棕色容量瓶中，于4 ℃冰箱中放置7 d备用。精密量取0.2，0.4，0.6，0.8，1.0和1.2 mL 1.14 mg/mL无水葡萄糖对照品溶液于6个20 mL具塞试管中，补充蒸馏水至2 mL混匀，加入1.5 mL DNS试液，摇匀后置沸水浴保持5 min，冷却至室温，定容至mL，摇匀。同时，以水为空白管对照，采用分光光度计测定540 nm波长处的吸光度。以吸光度（Y）为纵坐标，葡萄糖浓度（X）为横坐标，绘制标准曲线。取透明质酸发酵液适当稀释后，取1.0 mL溶液置20 mL具塞试管中，按照上述方法，自“补充蒸馏水至2 mL……”测定。根据标准曲线，计算供试品中还原糖含量。

透明质酸测定采用Bitter-Muir法[18-23]；发酵液黏度采用数显旋转黏度计测定，控温度35 ℃，根据不同黏度，选择合适转子及转速测定读数；电导率采用电导率仪测定，控温25 ℃测定；浊度测定，对发酵液稀释10倍后，采用浊度仪测定；发酵液中还原糖测定[12-14]，采用3, 5-二硝基水杨酸（DNS）比色法；发酵液中菌体含量测定[24]，采取干重法，根据透明质酸发酵液黏度液稀释一定倍数后离心取沉淀，洗涤1次，60 ℃真空干燥至恒质量，称取质量计算细胞浓度。

1.3 数据处理

采用Excel 2010软件进行数据统计及散点图绘制；SPSS 19.0软件用于相关性分析、偏相关分析、一元线性模型及二次项曲线模型构建；Matlab 2014软件用于构建BP神经网络模型；对3个批次发酵过程测得各参数取平均值用于相关性分析；3个批次各参数测得全部数据构建数学模型。

2 结果与分析

2.1 发酵液中菌体、透明质酸、还原糖含量变化曲线

对3个批次同一时间节点测得菌体量、透明质酸含量、还原糖含量取平均值，绘制曲线。结果如图1和图2所示。

从图1可知，0～2 h为菌体生长的调整期，菌体量很少；2～10 h为对数生长期，菌体快速生长繁殖；10～18 h菌体进入稳定期，菌体量始终保持在高位；18 h后进入衰亡期，菌体开始自溶。从图2可以看出，0～6 h透明质酸产量很少；6～16 h透明质酸快速积累；18 h后透明质酸开始降解，产量下降。还原糖含量2 h开始下降速度加快，主要用于菌体代谢繁殖及透明质酸前体合成；14 h菌体量趋于稳定，透明质酸前体大量合成，还原糖含量下降速度趋于平缓，18 h后还原糖含量趋于稳定。

2.2 还原糖含量与发酵液中各参数相关性分析

绘制散点图，考察发酵液中还原糖含量与透明质酸含量、菌体量、浊度、黏度、电导率变化规律的相关性。结果如图3所示。

由图3可以直观地看出，发酵液中还原糖含量与透明质酸含量、黏度相关性显著，与菌体量存在一定相关性，与电导率、浊度相关性不显著。采用SPSS软件进行pearson相关检验分析，表1给出还原糖含量与透明质酸（HA）、菌体量、浊度、黏度、电导率各参数之间相关性系数。由表1可知，当显著性水平p＜0.01时，发酵液中还原糖含量与发酵液浊度、电导率变化不存在相关性，与发酵液中透明质酸、菌体量、黏度变化呈显著性相关。

图1 菌体生长曲线

图2 透明质酸、还原糖含量变化曲线

图3 还原糖与各参数散点图

单纯利用相关系数来评价变量间的相关性还不够准确，还需要在剔除其他相关因素影响的条件下计算变量间的偏相关系数[16]。经偏相关分析，结果见表2。控制黏度及透明质酸含量2个变量，还原糖含量与菌体量相关性系数为0.300，显著性水平为0.433，远大于0.05，表明两者存在虚假性相关。控制其他2个变量，在显著性水平p≤0.01时还原糖含量与透明质酸、黏度变化规律呈显著性相关，相关系数分别为0.887和0.799。这是由于发酵液中葡萄糖除了少部分用于菌体生长繁殖外，绝大部分是作为底物用于合成透明质酸，其流程是葡萄糖经糖酵解（EMP）途径形成6-磷酸果糖，在酶的作用下形成6-磷酸葡萄糖胺，6-磷酸葡萄糖胺经乙酰化后合成尿苷二磷酸-N-酰基-氨基葡萄糖；尿苷二磷酸-葡萄糖醛酸通过糖醛酸途径合成。透明质酸合成酶交替地将尿苷二磷酸-N-酰基-氨基葡萄糖和尿苷二磷酸-葡萄糖醛酸以每分钟约100个糖单位的速度快速添加到HA分子链上，同时逐渐增长的HA链会穿过质膜被送到胞外基质中[10-11]。故发酵液中还原糖含量与透明质酸含量变化表现出较强的相关性。透明质酸水溶液由于其分子内和分子间的作用，具有非牛顿流体的流变学特性及黏弹性。透明质酸浓度较低，溶液的黏度随浓度变化相对较小，但浓度达到某一阈值时，溶液的黏度随浓度增加而快速提高，并表现出很强的相关性，因此发酵液中还原糖含量与黏度也表现出显著的相关性。结合两变量相关性及偏相关分析，发酵液黏度与发酵液中透明质酸均可预测发酵液中还原糖含量。考虑到发酵液黏度检测可通过旋转黏度计直接读数，方法简单；发酵液中透明质酸检测步骤繁琐、时间长、误差大情况，选定发酵液黏度作为描述发酵液中还原糖含量变化的唯一变量。

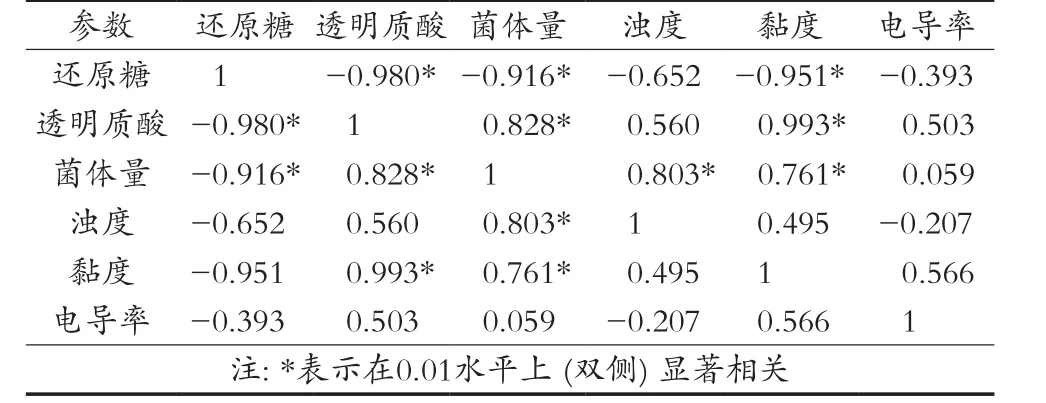
表1 还原糖与各参数相关系数

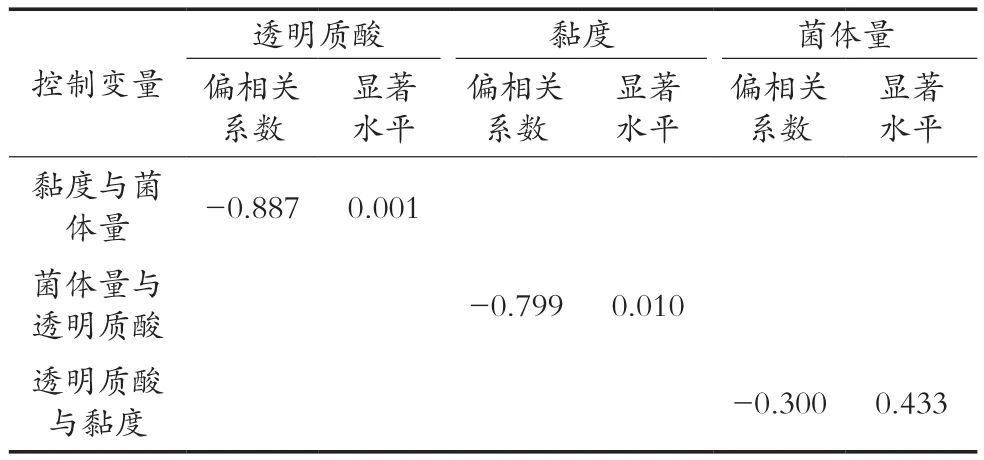
表2 还原糖与各参数的偏相关系数

2.3 构建数学模型

取3个发酵批次33组试验数据用于数学模型的构建，采用SPSS 19.0进行一元线性回归和二项式曲线回归分析；采用Matlab 2014构建BP神经网络模型。式中Y代表发酵液中还原糖含量，X代表黏度。

2.3.1 一元线性回归

对33组试验数据进行一元线性回归分析。Y=-0.380 3X+49.790 7。

经分析得，该线性方程复相关系数为0.993 2，判定系数R2=0.904 3，表明拟合效果较好；模型残差进行独立性检验DW=0.438 0，查询Durbin Watson table可以发现DW值恰好出在无自相关性的值域之中，认定残差独立，通过检验；回归方程显著性检验的概率p=0.000＜0.01，表明由自变量黏度和因变量还原糖含量建立的线性关系回归模型具有显著的统计学意义。

2.3.2 二次项曲线回归分析

二次项曲线回归分析模型为Y=53.211 1-0.848 0X+0.003 648X2。

经分析得，回归方程显著性检验的F=122.268 2，判定系数R2=0.968 3，回归方程显著性检验的概率p=0.000，说明模型高度显著。

2.3.3 BP神经网络

BP神经网络是一种按误差反向传播训练的多层前馈网络，具有很强的非线性映射能力，能很好地应用于非线性预测问题[25-27]。取33组试验数据构建3层结构BP神经网络[24-26]，输入层、输出层各一个神经元，分别代表发酵液黏度和发酵液中还原糖含量，输入层到隐含层的传递函数为logsig函数，隐含层到输出层之间选择purline线性传递函数。网格训练函数采用应用Levenberg-Marquardt优化后的trainlm训练函数算法。经多次试错法训练，最佳隐含层神经元个数为5个，训练后平均R值为0.997 43。

2.4 3种数学模型预测效果比较

对2019060401、2019060503其他2个批次13个试验样本进行发酵液黏度及还原糖含量检测；依据发酵液黏度值利用一元线性回归、二次项曲线回归分析及BP神经网络3种数据处理方法获得数学模型对发酵液中还原糖含量进行估测；将实测值与模型估测值进行对比，试验样本方差作为3种模型的评价指标检验模型的准确性，结果如表3所示。

表3 3种模型检验结果

由表3可知，利用BP神经网络模型的检验方差值最低，仅为0.169 4，算得标准差为0.411 5，表明利用BP神经网络建立模型预测准确率较高，可用于发酵液中还原糖含量的快速估测，二次项曲线回归分析模型与一元线性回归模型的预测准确率较低。

3 结论

在透明质酸发酵工业中，实时了解发酵液中还原糖含量，对掌握发酵过程状况、判定发酵终止时间、提前准备后续分离纯化工作有很大的指导意义。通过对发酵液中还原糖含量与透明质酸、菌体量、浊度、黏度、电导率变化规律的相关及偏相关分析，发酵液黏度、透明质酸含量、还原糖含量3个参数相关性显著。考虑到发酵液中透明质酸检测方法复杂、时间长、误差大等缺点，选择发酵液黏度作为估测发酵液中还原糖含量的唯一参数。对构建一元线性回归分析、二次项曲线回归分析及BP神经网络3种数据处理方法获得的数学模型进行验证分析，BP神经网络预测效果最为准确，方差为0.169 4，可以很好地预测发酵液中还原糖含量。由于试验样本有限，取33组试验数据，如能增大试验样本数量，利用BP神经网络构建模型对试验结果预测会更加精确。此外，黏度与透明质酸含量相关性非常显著，利用黏度亦可预测发酵液中透明质酸含量。