王莲仿生梯度蜂窝的面外压缩行为
王海任,李世强,刘志芳,雷建银,李志强,王志华
(太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024)
天然多孔材料如骨骼、贝壳、竹子、珊瑚、蜂窝等[1]包含梯度、层级、螺旋、多孔以及自组装等结构,为新型结构设计及高性能材料研制提供了新的方法和途径。多孔蜂窝具有高强度密度比、独特的响应特性和较长的平台应力区,在受到外力作用时具有较好的吸能特性,因而成为理想的吸能材料,被广泛应用于建筑、汽车、机械、航空航天、化学工程、纳米制造以及生物医学等领域[2]。传统蜂窝材料的静态与动态力学性能研究已经取得了丰硕的成果[3-6]。
随着研究的不断深入,研究人员提出了更多的设计方式来进一步提升蜂窝结构的力学性能,如蜂窝填充泡沫[7-8]、多层级蜂窝[9]、梯度蜂窝[10]、更换基体材料[11-12]以及引入负泊松比[13]等。其中蜂窝结构的梯度设计可以在不额外增加其他材料与蜂窝质量的前提下,仅仅依靠蜂窝质量分布的优化设计来提高其抗冲击性能,因此梯度蜂窝的抗冲击性能逐渐成为研究热点。研究蜂窝的能量吸收能力,需要首先掌握蜂窝的平台应力[14]。研究表明,在动态载荷作用下,多孔结构的抗压强度随着加载速率的增大而显著提高[15]。Reid 等[16]在研究木材类多孔材料时,基于冲击波模型建立了木材的动态压缩强度与准静态压缩强度之间的关系式。Ruan 等[17]通过模拟六边形蜂窝铝的面内冲击响应,研究了蜂窝铝动态压缩强度与冲击速度之间的关系。Qiao 等[18]对功能梯度蜂窝的动态冲击性能进行了研究,采用与Ruan 等相似的方法,通过拟合参数得到了一种计算动态压缩强度的方法,该方法具有计算简单、便于推广等优点。
本研究受自然界王莲叶片脉络启发,提出一种兼顾强度与刚度的圆形辐射状仿王莲脉络梯度蜂窝芯层结构,利用ABAQUS 有限元软件对其进行准静态与动态压缩数值模拟,分析其准静态压缩强度与相对密度的关系,并基于Ruan 等[17]和Qiao 等[18]提出的动态压缩理论,对面外梯度王莲仿生蜂窝结构在不同冲击速度下的动态压缩行为进行对比研究,探讨仿生蜂窝的动态压缩强度与相对密度、冲击速度之间的关系。
1 王莲结构仿生蜂窝设计
王莲叶片极强的承载能力源于其独特的蜂窝状叶脉结构。叶脉相交形成蜂窝状,叶脉的粗壮程度和蜂窝状结构的尺寸大小从中心到边缘逐渐变化,构成既美观又能承重的整体,王莲叶脉分布如图1(a)所示。对王莲叶脉的测量和分析表明,王莲叶脉分布符合Rudwig 植物形态学规律,各部分的长度比例满足黄金分割率[19]。图1(a)与图1(b)显示了仿生王莲叶脉的拓扑演化过程,在图1(b)所示的简化模型中,王莲叶脉结构中的径向叶脉和环形叶脉分别用放射状的径向网和环形网表示。梯度蜂窝压缩模型的尺寸关系如图1(c)所示。
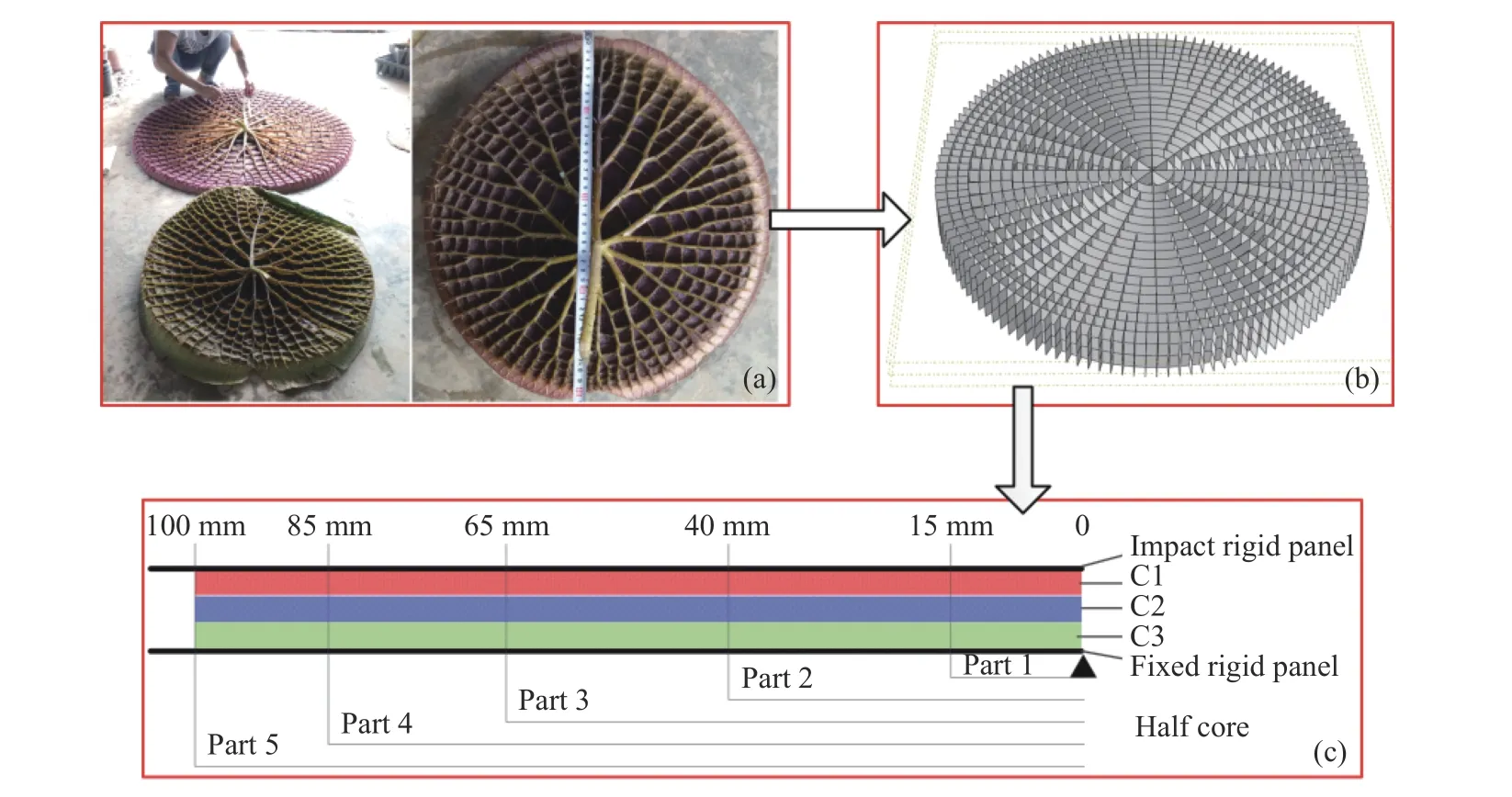
图1 仿生蜂窝设计策略: (a)王莲叶脉, (b)王莲叶脉简化模型,(c)梯度蜂窝压缩模型Fig. 1 Bionic honeycomb design: (a) natural Royal Water Lily vein structure, (b) a simplified model of natural Royal Water Lily vein, (c) compression model of gradient honeycomb
2 梯度仿生蜂窝面外压缩模型的建立
2.1 有限元模型的建立
王莲仿生蜂窝的准静态压缩与动态压缩使用ABAQUS/Explicit 软件模拟。根据图1(b)和图1(c)建立仿生芯层结构,冲击端面板与底部固定面板设置为刚体,壳单元的厚度为1 mm。在两个圆板的圆心处设置参考点,仿生蜂窝芯层放置在两板中间。仿生蜂窝半径R= 100 mm,各部分尺寸如图1(c)所示,总高度为21 mm,分为3 层,即C1、C2、C3 层,每层高7 mm。
仿生蜂窝和面板使用S4R 壳单元进行网格划分,网格大小为1 mm,共219 240 个单元,单元类型为有限薄膜应变,缩减积分,伪应变能控制设置为增强模式;接触设置为通用接触,用于避免前后面板与蜂窝发生穿透;摩擦系数设置为0.2;下面板参考点处设置为全约束,上面板参考点处设置一个固定压缩速度,如图2 所示。
准静态压缩的压缩速度为1 m/s,上面板以1 m/s 的速度均匀压缩仿生蜂窝,下面板保持固定。动态压缩采用相似的设置,压缩速度v设置为10~250 m/s。
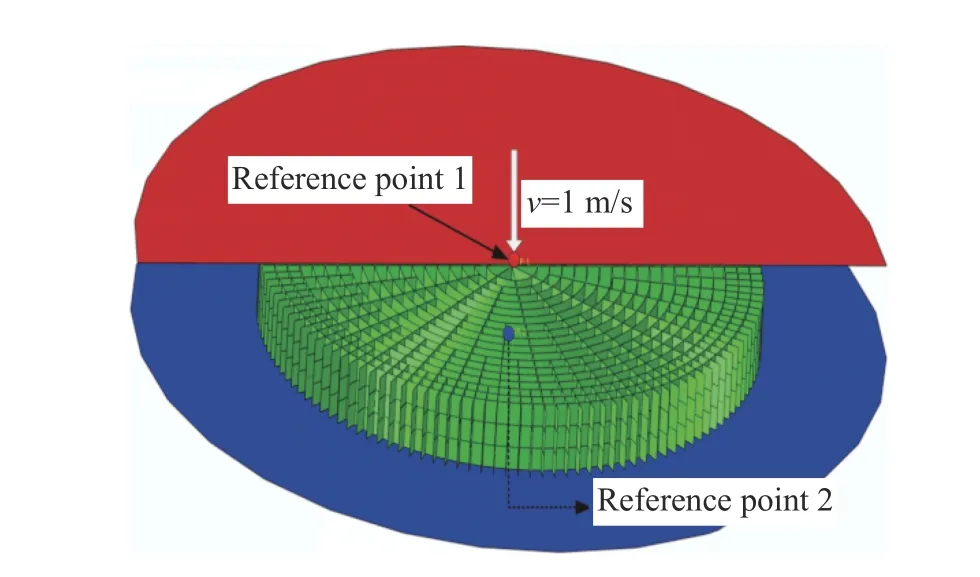
图2 面外压缩模型Fig. 2 Schematic diagram of out-of-plane compression
2.2 材料参数与相对密度
仿生蜂窝基体材料选择6060T4 铝合金[20],具体的材料参数如表1 所示,其中: ρ为蜂窝材料的密度,E为杨氏模量, μ为泊松比, σcY为屈服强度,Etan为切线模量。由于此类铝合金材料的应变率敏感性较低,因此有限元模拟过程中未考虑应变率效应。

表1 6060T4 铝合金材料参数Table 1 Material parameters of 6060T4 aluminum alloy

表2 为3 种类型的王莲仿生蜂窝结构参数,分别为面外负梯度仿生蜂窝Case 1、面外正梯度仿生蜂窝Case 2 以及均匀仿生蜂窝UG,3 种仿生蜂窝的面内梯度均为均匀,面外平均相对密度均为5%。其中:Case 1 仿生蜂窝的相对密度梯度从上到下分别为2%、5%和8%;Case 2 仿生蜂窝的相对密度梯度从上到下分别为8%、5%和2%;而对于均匀仿生蜂窝UG,不同的相对密度可以通过改变UG-5%的壁厚获得。

表2 模型类型与相关参数Table 2 Model and related parameters
2.3 有限元方法验证
评估模拟是否产生了正确的模态响应,最重要的验证方式是研究模型中的各种能量。采用显式动态算法来求解壳单元的准静态与动态压缩问题,需要进行速度敏感性验证以及能量平衡验证,同时需要检查以下能量:

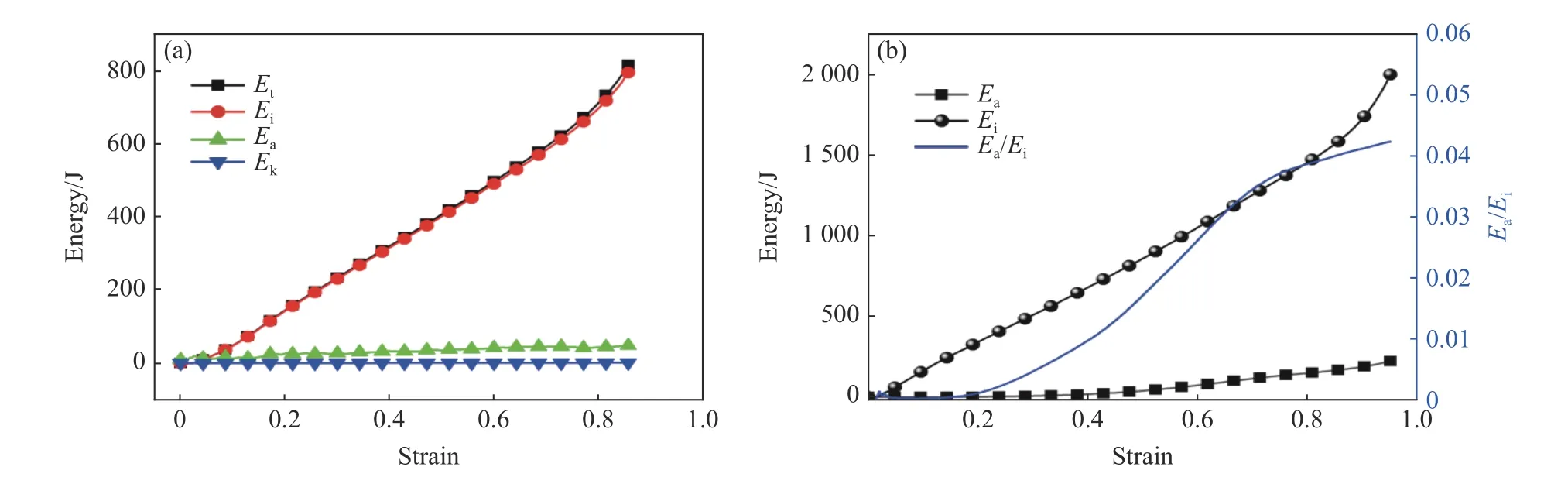
图3 相对密度为2%的均匀仿生蜂窝的能量验证: (a) 准静态压缩, (b) 250 m/s 动态压缩Fig. 3 Energy verification of uniform bionic honeycomb with relative density 2%:(a) quasi-static compression, (b) 250 m/s dynamic compression
3 结果及分析
3.1 均匀仿生蜂窝准静态面外压缩

图4 中的黑色曲线显示了均匀仿生蜂窝在准静态加载下的典型压缩应力-应变曲线,应力采用名义应力计算: σ=F/S,其中F为冲击端的反力,S为仿生蜂窝的初始面积,S= πR2。应变ε = δ/hc,其中δ 表示压缩距离,hc表示仿生蜂窝的高度。由图4可知 ε0很小,由式(4)可以求出相对密度为2%的均匀仿生蜂窝的准静态压缩强度 σnY为1.45 MPa。
为了进一步研究均匀仿生蜂窝的准静态压缩强度,对不同相对密度仿生蜂窝的准静态压缩行为进行分析。王莲仿生蜂窝的胞元形状类似于四边形蜂窝,四边形蜂窝压缩强度与相对密度之间的 关系可以表示为[23]
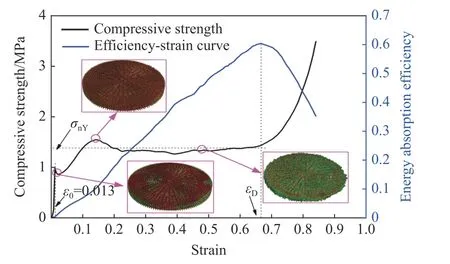
图4 均匀仿生蜂窝准静态压缩曲线与能量吸收效率Fig. 4 Quasi-static compression curve and energy absorption efficiency of uniform bionic honeycomb

式中:m= 1, ρ为仿生蜂窝的相对密度, σY为蜂窝基体材料的屈服强度。
面外压缩的六边形蜂窝在经历初始峰值之后具有软化的准静态响应,类似Ⅱ型结构的吸能特性[24],从图5 可以看出,本研究建立的仿生蜂窝在经历了初始软化相之后,响应更类似Ⅰ型结构的吸能特征,即经过短暂的Ⅱ型结构响应之后,后续结构响应基本上与I 型结构响应类似。同时,采用类似四边形蜂窝的压缩强度与相对密度的关系,根据图5 可以求出不同相对密度对应的m值,可以发现m值随着相对密度的增大而增大,并且随着相对密度的增大,m值逐渐趋近于1.1,如图6 所示。王莲仿生蜂窝的面外压缩强度优于四边形蜂窝、六边形蜂窝以及菱形蜂窝的面外压缩强度。考虑到计算误差,本研究计算采用的m值介于 0.9~1 之间。
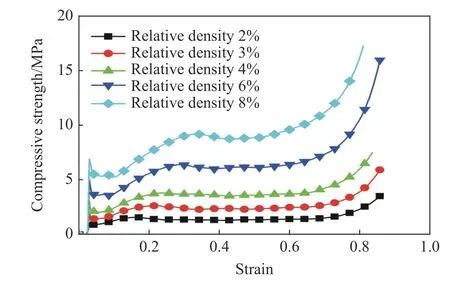
图5 不同相对密度均匀仿生蜂窝准静态压缩曲线Fig. 5 Quasi-static compression curves of bionic honeycomb with different relative densities
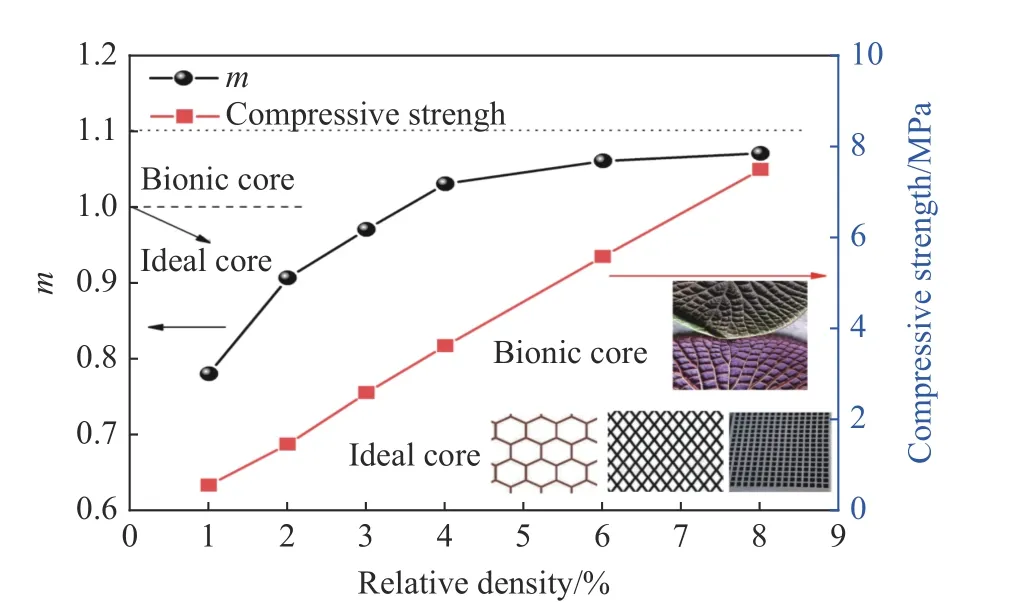
图6 不同相对密度的m 值与准静态压缩强度Fig. 6 m and quasi-static compressive strengths of different relative densities
3.2 均匀仿生蜂窝面外动态压缩

综上所述,通过结合动态压缩强度的两种表示形式,可以得到相对密度、冲击速度共同影响下均匀仿生蜂窝的面外压缩强度公式,方便后续的理论计算。式(8)的关键参数为A,对A进行分析可知,图7 的拟合参数A实际上隐含了Qiao 等的研究结论,即随着冲击速度的增大,A对几何参数不敏感,表明式(8)在中高速冲击下是精确的,但是对于低速冲击,利用式(8)得到的压缩强度会产生一定的误差。对相对密度为4%与8%的均匀仿生蜂窝在不同冲击速度下的模拟结果与理论结果进行对比,结果如图8 所示。由图8 可以看出,均匀仿生蜂窝动态压缩理论值与模拟值对比具有较好的一致性,模拟解与理论解的相对偏差基本都在10%左右。理论解在较低冲击速度下与模拟解的差异较大,随着冲击速度的增大,两者之间的差异逐渐减小。另外,随着仿生蜂窝相对密度的增大,理论解与模拟解的相对偏差逐渐缩小。
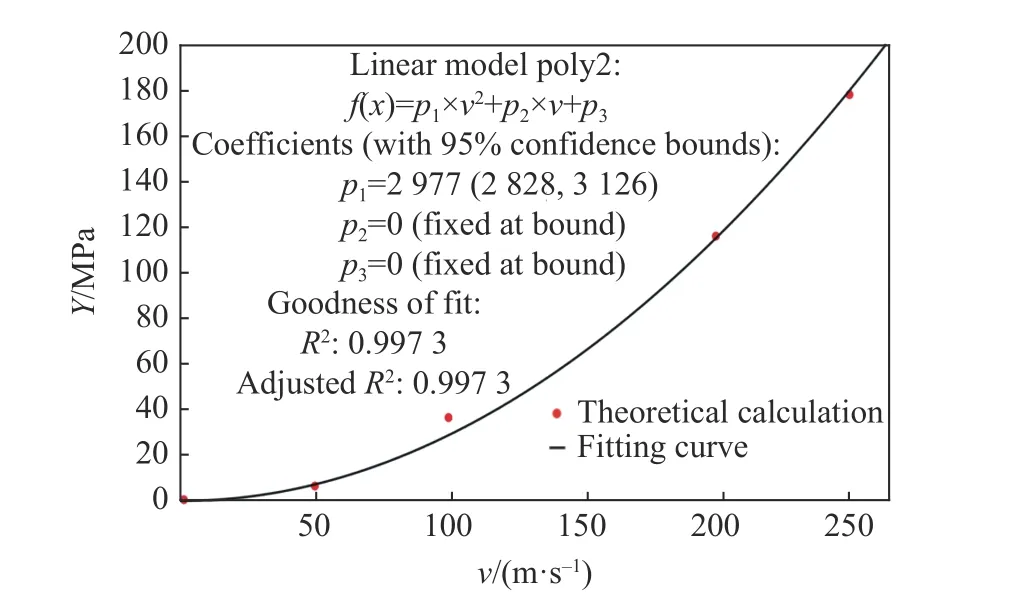
图7 动态参数A 的拟合曲线Fig. 7 Fitting curves of dynamic parameter A
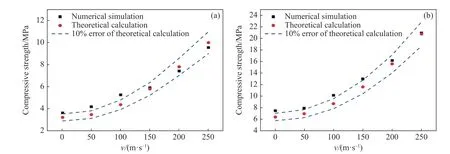
图8 均匀仿生蜂窝动态压缩强度理论值与模拟值对比:(a)相对密度4%,(b)相对密度8%Fig. 8 Comparison between theoretical calculations and simulation values of dynamic compressive strengths of uniform bionic honeycomb: (a) relative density 4%, (b) relative density 8%
3.3 面外梯度仿生蜂窝动态压缩
为了研究面外梯度仿生蜂窝的动态压缩性能,对由2%、5%、8%相对密度组成的两类面外梯度仿生蜂窝进行了动态压缩,仿生蜂窝分别表示为面外负梯度(C1、C2、C3 层的密度梯度分别为2%、5%和8%)仿生蜂窝Case 1 与面外正梯度(C1、C2、C3 层的密度梯度分别为8%、5%和2%)仿生蜂窝Case 2。作为参考,对相对密度为5%的均匀仿生蜂窝UG-5%的动态压缩行为也进行了研究。同时,利用式(8),对不同冲击速度下不同相对密度的仿生蜂窝的动态压缩强度进行了计算,并与模拟结果进行了对比。面外梯度仿生蜂窝在不同冲击速度下的压缩强度曲线与能量吸收效率曲线如图9 所示。
由图9 可以看出,不同面外梯度仿生蜂窝在低速(10 m/s)、中速(50 和100 m/s)和高速(200 m/s)冲击下的变形模式与压缩强度不同。在不同冲击速度下,Case 1 与UG-5%蜂窝均为渐进压缩模式。在10 m/s 冲击速度下,两种面外梯度仿生蜂窝的压缩强度曲线基本一致,表现为阶梯状模式,表明两者的变形模式类似,即准静态抗压强度较低的芯层依次被压缩。Case 1 蜂窝表现为C1-C2-C3 层渐进压缩,而Case 2 蜂窝则是靠近固定端的C3 层先被压缩,表现为C3-C2-C1 层渐进压缩。当冲击速度增大到50 m/s时,两种面外梯度仿生蜂窝的压缩强度曲线开始不同,在初始冲击阶段,Case 2 蜂窝会产生较高的初始应力峰值,而Case 1 蜂窝的初始应力峰值较低。这是由于在惯性作用下,Case 2 蜂窝中准静态压缩强度最高的C1 层会优先被轻微压缩,产生大约6%的应变,而Case 1 蜂窝的C1 层准静态压缩强度最低,因此产生的初始峰值也低。随后Case 2 与Case 1 蜂窝的应力-应变曲线再次重合,表明压缩过程重新变为准静态抗压强度较低的芯层依次被压缩。在100 m/s 冲击速度下,仿生蜂窝的变形模式与冲击速度为50 m/s 时基本一致,但Case 2 蜂窝的初始应力峰值更高,C1 层持续压缩时间变长且压缩量增至18%。在200 m/s 冲击速度下,两种面外梯度仿生蜂窝压缩强度曲线的差异明显变大,表现为Case 1 蜂窝压缩强度曲线依旧保持为阶梯状,而Case 2 蜂窝的压缩强度曲线呈现“U”形变化。这是由于在高速冲击下,惯性效应进一步增强,芯层初始压溃呈现出渐进压溃模式,当冲击波传播至远端时,各层的压溃和密实化取决于其静态压缩强度,密实化依次出现在强度较低的芯层。对于Case 2 蜂窝,当C1 层压缩量接近50%时,C1 层不再压缩,C2 与C3 层发生耦合变形并开始被压缩,但准静态压缩强度较低的C3 层优先被压缩,然后C2 层被压缩,最终C1 层被压缩,Case 2 蜂窝整体达到密实化,这也使得Case 2的压缩强度由高到低再变高。另外,由图9 还可以看出,采用式(8)计算得到的相对密度为5%的仿生蜂窝在不同冲击速度下的压缩强度(图9 中蓝色直线)与模拟值(图9 中绿色曲线)差异较小,同时对比两种梯度芯层在不同冲击速度下各层的压缩强度与理论值,表明各层的动态压缩强度可以由均匀仿生蜂窝动态压缩强度分别计算得出。
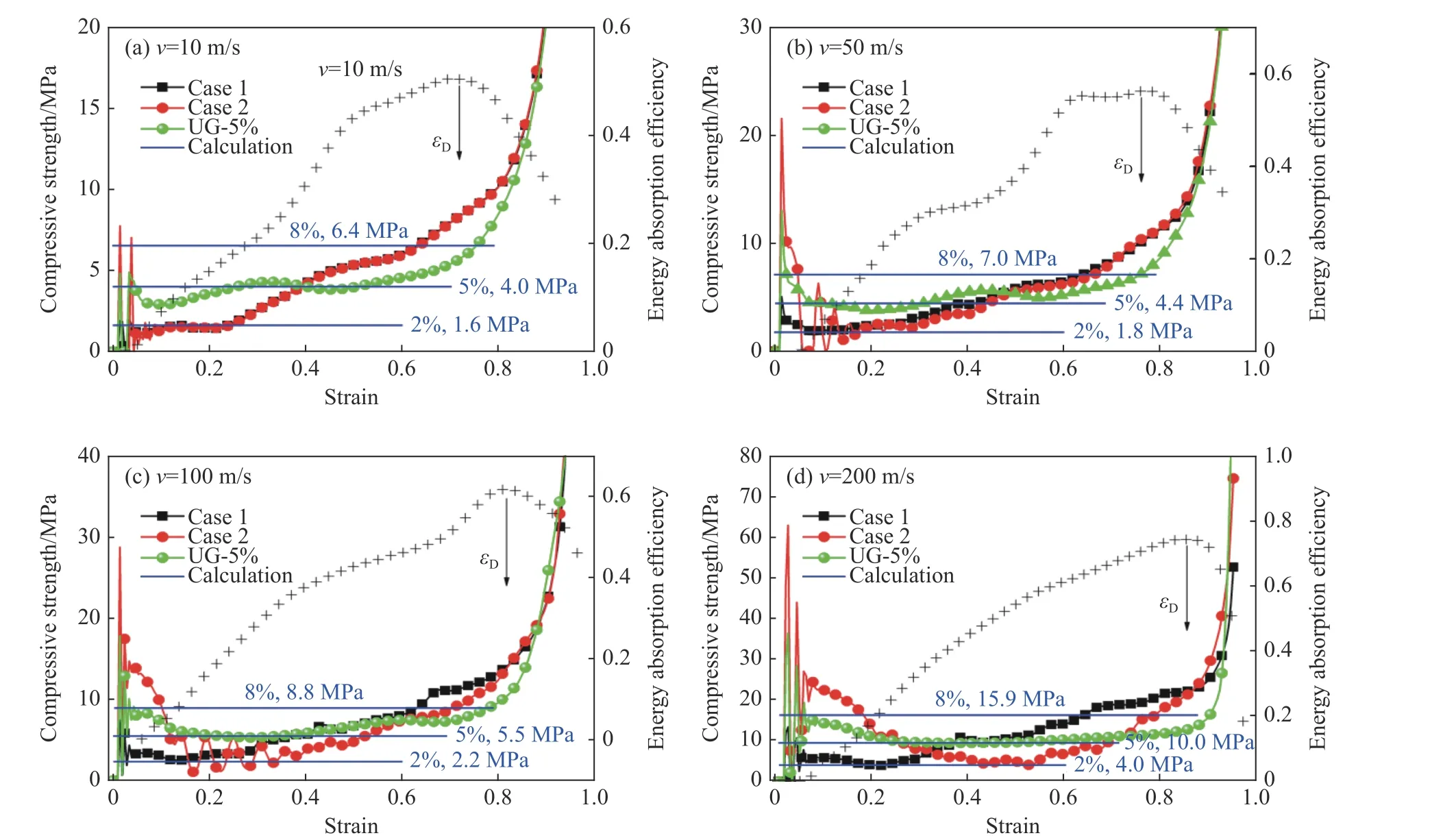
图9 面外梯度仿生蜂窝在不同冲击速度下的压缩强度曲线与能量吸收效率曲线Fig. 9 Compressive strength curves and energy absorption efficiency curves of out-of-plane gradient bionic honeycombs under different impact velocities
4 结 论
基于王莲脉络模型,设计了一种新型仿生蜂窝结构,通过调节结构各部分的相对密度,对均匀蜂窝与面外梯度蜂窝的准静态压缩、动态压缩性能进行了研究,得出以下主要结论。
(1)利用ABAQUS 有限元软件对新型王莲仿生蜂窝结构进行了准静态与动态压缩数值模拟,通过对均匀仿生蜂窝的静态压缩研究,得到了此仿生蜂窝准静态压缩强度与基体材料屈服应力之间的关系,基于现有的动态压缩理论,探讨了仿生蜂窝的动态压缩强度与相对密度、冲击速度之间的关系,结果表明,动态压缩强度的计算值与有限元模拟值之间的差异随着冲击速度的增大逐渐减小。
(2)面外梯度王莲仿生蜂窝结构在不同冲击速度下的动态压缩行为研究表明,低速冲击时(10 m/s),两种面外梯度仿生蜂窝的压缩强度曲线基本一致,表现为阶梯状,两者的变形模式类似,即准静态抗压强度较低的芯层依次被压缩。在高速冲击下(200 m/s),梯度芯层压溃模式与芯层梯度分布方式密切相关,Case 1 蜂窝压缩强度曲线依旧保持为阶梯状渐进压缩模式,而Case 2 蜂窝的压缩强度呈现“U”形变化,初始压溃呈现出渐进压溃模式,当冲击波传播至远端时,各层的压溃和密实化取决于其静态压缩强度,密实化依次出现在强度较低的芯层。梯度芯层每层的动态压缩强度可以由均匀仿生蜂窝动态压缩强度分别计算得出,此结果可为王莲仿生蜂窝结构的进一步优化设计提供参数依据。
感谢中国科学院西双版纳热带植物园园林园艺部吴福川副部长提供的王莲高清图片与有益的讨论。

