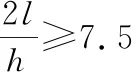双材料层合梁弯曲正应力的弹性解与试验分析

李苗苗，吴 晓

(1.常德职业技术学院土建系，湖南 常德 415000；2.湖南文理学院机械工程学院，湖南 常德 415000)

1 引 言

在土木、机械等实际工程中，许多钢结构、混凝土承载构件都是螺栓连接的层合梁或高强粘合剂粘合的层合梁。为了使学生掌握理解层合梁及粘贴片材对混凝土梁加固的应用，文献[1]把销钉连接构件作为应力试验进行应力分析，文献[2，3]对螺栓或销钉连接构件的弯曲进行了理论研究。文献[4]采用材料力学方法对组合梁的弯曲应力进行了分析，文献[5]用弹性力学方法研究了双材料叠合悬臂梁的弯曲。文献[6，7]]研究了采用粘贴片材对混凝土梁的加固，文献[8]以专著阐述了复合材料层间应力。文献[9-10]研究了复合曲梁的力学性能，并把复合曲梁的应力测量引入材料力学试验教学中。文献[11]把胶结叠合梁的弯曲试验引入了试验教学。文献[15]研究了基于微分求积法的钢筋混凝土梁静力分析，文献[16]研究了超静定连续梁弹塑性过程分析的单位荷载法。文献[17]研究了任意光滑梯度变化的功能梯度材料纯弯曲梁的弹塑性分析。

由以上文献可知，层合梁在工程实际中得到了广泛应用，而关于高强粘合剂粘合的层合梁弯曲时的弹性解还未见有关文献给出。所以，研究层合梁的弯曲应力计算理论及开展层合梁的弯曲应力试验是有实际意义的。本文采用弹性力学方法推导出了双材料层合梁弯曲正应力的计算公式，为层合梁及粘贴片材对混凝土梁加固的弯曲计算提供理论依据。通过层合梁的弯曲应力试验，验证了弹性力学方法推导的双材料层合梁弯曲正应力计算公式的正确性。

2 梁弯曲弹性解

2.1 中性轴位置的确定

以两端简支双材料梁为例，采用材料力学方法确定双材料梁的中性轴。由材料力学可知，梁弯曲时的正应力公式为：

(1)

式中，i=1时E1为材料1的弹性模量，i=2时E2为材料2的弹性模量，ρ为曲率半径。

利用式(1)可得双材料层合梁弯曲时横截面轴向静力平衡方程为：

(2)

式中，y0为中性轴到梁下层底面的距离。

由式(2)积分可得：

(3)

由式(3)可求得：

(4)

2.2 弯曲应力公式

双材料层合梁由于组成梁的材料弹性模量不同，双材料层合梁弯曲时，其中性轴不再位于梁高度的1/2处，这样层合梁弯曲时拉伸区和压缩区的应力表达式各不相同。

参阅文献[12，13]，可设双材料层合梁的弯曲应力表达式为：

σyj=Ajy3+Bjy2+Cjy+Dj

τxyj=-x(3Ajy2+2Bjy+Cj)

(5)

式中，j=1,2，j=1时，代表拉伸区，j=2时，代表压缩区。

图1所示简支双材料层合梁上、下表面的边界条件为：

y=y0，σy1=0，τxy1=0；

y=y0-h，σy2=-q，τxy2=0

(6)

梁右端x=l处静力平衡方程为：

(7)

梁弯曲时中性层处连续条件为：

y=0，σx1=σx2=0，σy1=σy2，τxy1=τxy2

(8)

把式(5)代入式(8)中第二、第三分式中可得：

C1=C2，D1=D2

(9)

把式(5)代入式(8)中第一分式中可得：

x2B1+2K1=0，x2B2+2K2=0

(10)

由于式(10)对x取任意值都成立，可得：

B1=B2=0，K1=K2=0

(11)

把式(5)代入式(6)中可得：

-A2(h-y0)3-C2(h-y0)+D0=-q

3A0(h-y0)2+C0=0

(12)

由式(9)、式(12)可以求得：

(13)

把式(5)代入式(7)中可得：

(14)

把式(13)代入式(14)中可求得：

(15)

把以上有关各式代入式(5)中，并考虑层合梁的宽度，可得双材料层合梁弯曲时拉伸区、压缩区应力表达式：

(16)

当E1=E2、b=1时，式(16)即退化为文献[12]给出的单材料梁弯曲应力的经典弹性解。

3 试验及理论分析

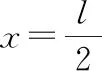
图1 双材料层合梁

层合梁的计算参数分别为：l=150mm，b=20mm，h1=h2=20mm，q=10kN/m。紫铜材料弹性模量为112GPa，铝合金材料弹性模量为72GPa。下面把试验结果、材料力学方法计算结果与本文方法理论计算结果均列在表1、表2中，以便讨论分析。在表1、表2中，层合梁上层材料为紫铜、下层材料为铝合金，误差分别为材料力学方法计算结果与试验结果误差、本文方法计算结果与试验结果的误差(注：表1、表2中的误差值均为以理论计算结果为标准值与试验结果的误差)。

由文献[14]，可以求得图1所示简支双材料层合梁任意截面拉伸区及压缩区的弯曲正应力计算公式分别为：

(17)

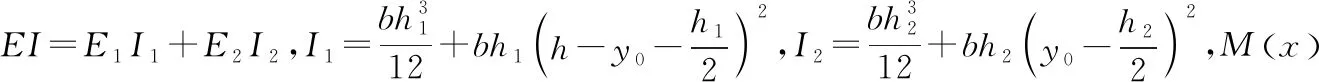
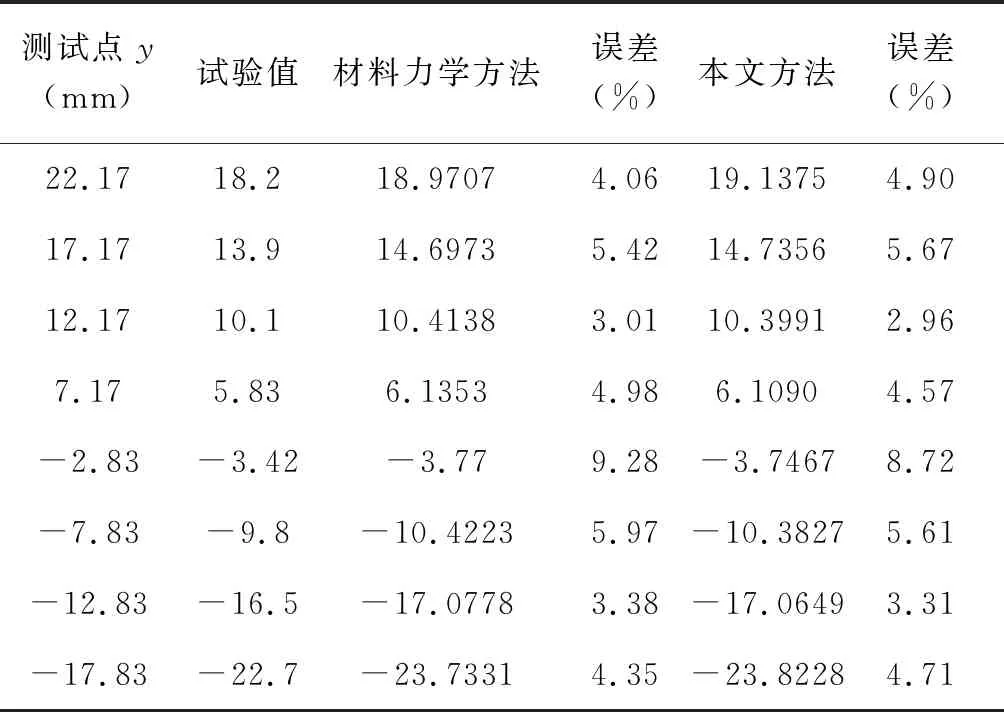
表1 层合梁的弯曲正应力(MPa)(x=0，y0=22.17mm)

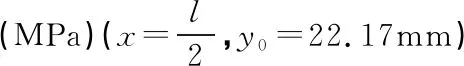
表2 层合梁的弯曲正应力

对表1、表2进行分析可以知道：

弹性力学方法计算结果、材料力学方法计算结果与试验结果基本吻合。表1、表2共16个测试点，弹性力学方法对测试点的计算结果大部分优于材料力学方法对测试点的计算结果。但对拉伸区最大正应力、压缩区最小正应力测试点的计算结果，材料力学方法的计算结果优于弹性力学方法的计算结果。因为弹性力学方法给出的层合梁弯曲正应力公式考虑了剪切变形对层合梁弯曲正应力的影响，所以弹性力学方法对测试点的计算结果大部分优于材料力学方法对测试点的计算结果。

当E1=E2时，式(16)即退化为文献[12]给出的单材料梁弯曲应力的经典弹性解：

(18)

当E1=E2时，式(17)即退化为文献[14]给出的单材料梁弯曲应力的材料力学解：

(19)

把式(16)与式(17)对比、式(18)与式(19)对比，可以看出，式(16)比式(17)多两项修正项、式(18)比式(19)多两项修正项，而且多余两项修正项均与梁截面弯矩无关，这说明经典弹性解给出的梁弯曲应力计算公式考虑了剪力的影响。因此，经典弹性解给出的梁弯曲应力公式计算精度要高于材料力学方法给出的梁弯曲应力公式计算精度。

(20)

以单材料梁弯曲应力的经典弹性解为标准，若采用材料力学方法计算，单材料梁弯曲应力的经典弹性解与单材料梁弯曲应力的材料力学解的误差应不超过5%，即满足下式：

(21)

把式(20)代入式(21)中可得：

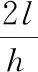
(22)

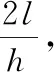
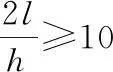
本文弹性力学方法对测试点的计算结果与试验结果存在一定的误差。笔者认为，造成误差的原因有几个方面：一是双材料层合梁在热成型、加工过程中有可能存在制作缺陷；二是试验装置本身就存在试验误差；三是试验机对双材料层合梁中点加载时，试验机压头有可能没有完全压在梁中点，使梁中点存在扭矩作用；四是对双材料层合梁测试点粘贴应变片时没有准确粘贴到位；五是对层合梁实现简支承不理想，由于实验室试验台用橡胶垫刚度相对层合梁的刚度较小、没有找到硬刚度橡胶垫，导致模拟出加载在图1所示简支双材料层合梁上的近似均布载荷不理想。以上原因都会导致本文方法计算结果与试验结果产生一定的误差。

4 结 论

(1)采用弹性理论方法得到了双材料层合梁拉伸区及压缩区弯曲正应力的表达式，当E1=E2、b=1时，式(16)即退

化为弹性力学给出的单材料梁弯曲应力的经典弹性解。通过层合梁的弯曲应力试验，验证了弹性力学方法给出的双材料层合梁弯曲正应力计算公式的正确性。

(2)弹性力学方法计算结果、材料力学方法计算结果与试验结果基本吻合。但是弹性力学方法给出的层合梁弯曲正应力公式考虑了剪切变形对层合梁弯曲正应力的影响，所以弹性力学方法对测试点的计算结果大部分优于材料力学方法对测试点的计算结果。