基于凸轮曲线理论的机械手对ROV本体位姿影响效果分析

王 妍，杨明岩，张丽巍，高 胜

(东北石油大学机械科学与工程学院，黑龙江 大庆 163318)

UVMS(underwater vehicle-manipulator system)即ROV(remote operated vehicle)机械手系统可代替人工进行水下作业，完成海底样品采集、打捞、设备定位等任务[1]。UVMS本身是一个动力耦合系统，在进行作业时因与作业目标之间的动力学耦合作用会造成作业目标的运动误差。目前对于此类误差的补偿大多是通过控制ROV的运动来实现，然而对于细微误差应用此方法则很难满足精度要求。这是因为，虽然通过控制机械手的运动可以弥补运动中产生的微小误差，但机械手运动对ROV位姿的影响反过来又会影响到机械手末端位置，继而影响补偿效果，因此合理的机械手运动方式对误差的补偿效果至关重要。

基于此，本文采用机构学凸轮曲线理论[2]，推导出等加速度型、5次多项式型、变形梯形、摆线型、合成正弦和变形正弦运动曲线方程，假定作业目标质量忽略不计，研究分析机械手以这6种运动曲线执行相同动作对ROV本体位姿产生的影响，间接评价机械手补偿误差的效果，研究成果对利用机械手运动补偿作业误差具有一定的参考价值。

1 UVMS动力学模型建立

在描述UVMS运动之前，首先参考文献[3]的方法建立UVMS的坐标系，并将其分为固定坐标系与运动坐标系。这里以ROV和四自由度机械手构成的UVMS为研究对象，建立的UVMS坐标系如图1所示。

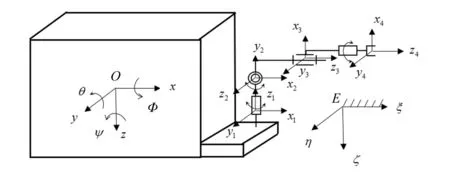
图1 UVMS坐标系

固定坐标系E-ξηζ：选定海中任一点为坐标系原点E，Eξ轴在水平面内，并以ROV的艏部为其正方向，Eζ轴与Eξ垂直且正方向指向地心，Eη轴与ξζ平面垂直，并以ROV右舷为其正方向[4]。

运动坐标系O-xyz：ROV在水中存在静平衡问题，先对ROV本体进行配重，使ROV重心和浮心重叠在ROV几何中心上，至少使ROV重心和浮心重叠保持在其横、纵中剖面的交线上。将ROV的浮心规定为运动坐标系的原点O，规定Ox轴正方向指向ROV的艏部，ROV的右舷方向为Oy轴的正方向，Oz轴垂直于Ox轴和Oy构成的平面，其正方向指向地心。

文中部分变量的含义见表1和表2。表中将固定坐标系简称为定系，将运动坐标系简称为动系。

表1 固定坐标系变量

表2 动坐标系变量

基于准拉格朗日公式(Quasi-Lagrange)及其他相关研究[5-6]，UVMS的一般动力学方程为：

(1)

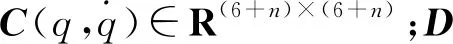
ROV和机械手构成动力学耦合系统，机械手运动时产生的交互作用力会引起ROV的位姿变化，而ROV位姿的变化又会对机械手的作业精度产生影响，要想保证机械手误差补偿的效果，就要研究机械手运动对ROV位姿产生的影响。目前研究此类问题时机械手多采用等加速型的运动方式，但无法判断机械手采取的这种运动方式是否合理。本文借助机构学中的凸轮曲线理论，推导出多种运动曲线方程，并将其应用在UVMS的动力学分析上，找出最适合应用于机械手控制的加速度曲线。

2 凸轮曲线描述与推导

惯性负载由静止移动到另一点刚好处于静止状态，在此过程中运动随时间变化规律通常用机构学中的凸轮曲线理论来研究。理想的运动轨迹是平滑的，即从始点到终点整个运动过程中有连续的位移、速度、加速度，起始点和终点的连续条件为：

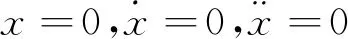
式中:t为运动时间；tf为运动到终点所需时间；x为位移；xf为运动到终点的位移。

在惯性负载运动过程中，其加速度应尽量小一些，且在运动过程中应合理地分配加速度，这样会产生较小的惯性载荷，使系统运动更加平稳。

设定时间和位移的变化为

t/tf=T,x/xf=X

(2)

将x(t)统一为X(T)，再设定dx/dT=V，d2x/dT2=A，则有

(3)

以下按无量纲形式对几种典型凸轮曲线进行描述和推导。

1)等加速度型。

等加速度型运动加速度Am为常数，其表达式为

(4)

对式(4)积分，代入边界条件V(0)=V(1)=0，得惯性负载的速度表达式为：

(5)

对式(5)积分，代入边界条件X(0)=0和X(1)=1，得惯性负载位移表达式为：

(6)

其中Am=4。

2)摆线型。

摆线型角加速度的曲线为正弦曲线，Am为加速度最大值，加速度表达式为：

A=Amsin(2πT) 0≤T≤1

(7)

对式(7)进行积分，由其边界条件V(0)=0或V(1)=0，可得惯性负载速度表达式为：

(8)

对式(8)进行积分，代入边界条件X(0)=0和X(1)=1，得惯性负载位移表达式为

(9)

其中Am=2π。

3)5次多项式型。

5次多项式型角加速度曲线为3次多项式，其表达式为：

A=aT3-bT2+cT0≤T≤1

(10)

对式(10)进行连续两次积分有：

(11)

式中：a,b,c,d,e为多项式系数。

其边界条件为A(1)=0,V(0)=V(1)=0,X(0)=0且X(1)=1,可得到d=e=0，同时有：

计算可得a=120，b=-180，c=60。则5次多项式运动规律可定义为

(12)

4)合成正弦。

合成正弦方式的加速度曲线为两个不同运动周期的正弦曲线叠加，其加速度表达式为：

A=A1+A2=asin(2πT)+bsin(6πT)

0≤T≤1

(13)

对式(13)连续两次积分有

(14)

利用边界条件X(0)=0和X(1)=1，可直接得到c=1和d=0。速度边界条件为V(0)=0或V(1)=0,则有：

(15)

如图2所示，从削波角度分析，两条独立正弦曲线A1和A2需满足：

(16)

图2 合成正弦参数的选择

由图可知，当a/b减小时，削波趋势加强，但在t=0～0.2这段时间加速度曲线变陡。取a=5b，可得合成正弦运动表达式为

(17)

5)变形正弦。

变形正弦由两条不同角频率的正弦曲线合成，其加速度表达式为：

(18)

对式(18)进行积分，通过其相应边界条件限定，得到速度和位移表达式分别为：

(19)

(20)

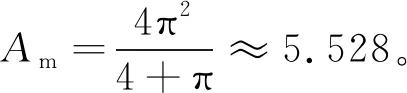
6)变形梯形。

变形梯形由正弦曲线与直线合成，加速度表达式为：

(21)

对式(21)进行积分，通过其相应边界条件限定，得到速度和位移表达式分别为：

(22)

(23)

3 多种类型凸轮曲线对比分析

图3给出了上述6种运动规律的加速度、速度、位移曲线。从图中可以看出，6种运动方式凸轮曲线在T=1以内满足位移X=1且起始速度V(0)和终点速度V(1)均为0的运动控制要求。同时可以看出位移曲线变化趋势较相似，速度与加速度曲线变化存在较大差异。6种运动方式只有等加速型的加速度曲线不连续，摆线类型具有最大加速度6.283 2，而等加速型的加速度最小为4。速度曲线中，变形正弦运动方式下具有最小速度峰值1.759 6，5次多项式为1.875 0，其他曲线的速度峰值均为2[7]。表3给出了6种凸轮曲线的加速度峰值和速度峰值的统计数据。

图3 不同类型凸轮曲线

表3 不同类型凸轮曲线加速度峰值和速度峰值

4 机械手以不同加速度进行运动对ROV位姿的影响

在6种加速度曲线方程和式(1)UVMS动力学方程的基础上，应用ADAMS软件对UVMS进行运动学、动力学分析，分析机械手按不同运动曲线执行相同动作对ROV位姿产生的影响。

ROV本体质量为900 kg,外形尺寸为2 100 mm× 1 200 mm×2 060 mm。四自由度机械手收缩时长度为760 mm，完全伸出时长度为980 mm。机械手材料为GCr15，材料密度为7 801 kg/m3，机械手在空气中质量为40 kg。令机械手在时间tf=1 s内由收缩状态到完全展开，其中关节1转动角度为π/12，关节2转动角度为5π/12，关节3伸长量为220 mm，腕部转动关节4转动角度为π/2。由t/tf=T和x/xf=X及6种凸轮曲线的位移方程，可以得到各运动关节的量纲位移方程。

以等加速型运动为例，此时机械手各关节位移与时间关系的表达式为：

(24)

(25)

(26)

(27)

对于其他形式的加速度曲线，可利用相同方式得到机械手各关节位移与时间关系的表达式。

按不同加速度类型曲线控制机械手运动，可以得到ROV在x,y,z方向的位置偏差和绕x,y,z轴角度偏差的曲线如图4和图5所示，ROV绝对位姿偏差统计数据见表4和表5。

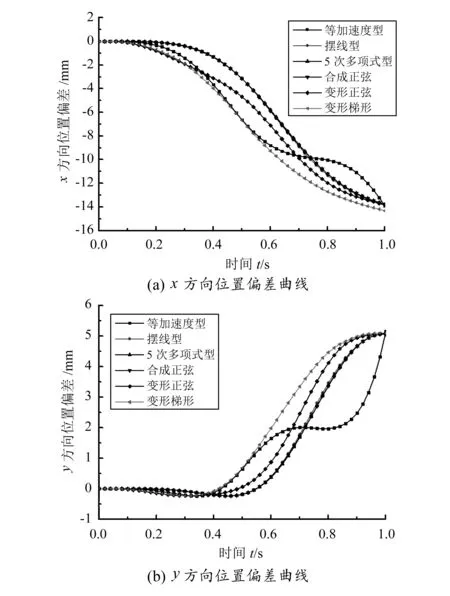
图4 不同加速度运动规律对ROV位置偏差的影响

图5 不同加速度运动对ROV角度偏差的影响

从图4和图5中可以看出，等加速度型方式下机械手运动对ROV位姿偏差的影响与其他几种方式有明显区别。等加速度型方式下机械手运动过程中ROV位置偏差曲线和角度偏差曲线波动剧烈，说明在此运动方式下机械手和ROV之间存在强烈的耦合作用，机械手运动的交互作用力很容易对ROV位姿产生影响。从表4、表5可以看出，等加速型方式下ROV绝对位姿偏差最大值比较大，说明机械手停止运动时ROV位置偏差较大。

表4 不同加速度运动规律对ROV绝对位置偏差统计数据

表5 不同加速度运动规律对ROV绝对角度偏差统计数据

机械手在摆线型、5次多项式型和合成正弦方式下运动ROV位姿偏差曲线非常相近，并且曲线较为光滑。从表4、表5可以看出,摆线型运动方式下绝对位姿偏差平均值、绝对位姿偏差最大值都要小于5次多项式型和合成正弦方式，说明在摆线方式下ROV姿态受机械手运动影响较小，ROV位置偏差和角度偏差波动较平缓。5次多项式型方式下绝对位姿偏差平均值、绝对位姿偏差最大值大于摆线型和合成正弦方式，说明该方式下ROV位置偏差曲线和角度偏差曲线波动较为剧烈，在此运动方式下ROV位姿受机械手运动影响大。合成正弦方式下ROV绝对位姿偏差最大值和绝对位姿偏差平均值介于摆线型和5次多项式型中间，与摆线方式相比，机械手在此运动方式下ROV位置偏差和角度偏差曲线波动稍显剧烈。

从变形梯形方式下ROV位姿偏差曲线可以看出，在0.4 s后偏差值迅速变大，ROV位姿变化剧烈。在机械手动作结束前的一小段时间内ROV位置偏差和角度偏差增长缓慢，在此时间段内ROV受机械手运动影响较小。从表4、表5可以看出，变形梯形方式下ROV的绝对位置偏差最大值在x,y,z方向分别为14.315 4 mm、5.104 9 mm和3.643 1 mm，绕x,y,z轴转动的绝对角度偏差最大值分别为0.603 2°、0.220 6°和0.885 3°，明显大于其他几种运动方式，说明在此运动方式下ROV位置偏差和角度偏差变化幅度最大。

从图4、图5可以看出，变形正弦方式下ROV位置偏差和角度偏差曲线与摆线型、5次多项式和合成正弦方式下的曲线较相近，波动程度比其他3种方式下的曲线稍显剧烈，但在0.8～1.0 s时间段内ROV位置偏差和角度偏差变化缓慢。从表4、表5可以看出,变形正弦下绝对位置偏差最大值在x,y,z方向分别为13.775 2 mm、5.060 9 mm和3.596 1 mm，绕x,y,z轴转动的绝对角度偏差最大值分别为0.597 3°、0.202 7°和0.882 8°，都要小于其他几种运动方式，说明在此运动方式下ROV位置偏差和角度偏差变化幅度最小。

通过上述分析可知，从ROV位置偏差极值和角度偏差极值方面考虑，变形正弦方式效果最好，其次为摆线型、合成正弦和5次多项式型，再者是等加速度型，最后为变形梯形。在此基础上，还有必要分析机械手以不同运动方式对ROV位姿稳定性影响的差异。对ROV位置偏差和角度偏差函数求导，利用位置偏差导数和角度偏差导数分析机械手以不同加速度方式运动时ROV位姿变化稳定性的差异。不同加速度运动规律下ROV位置偏差导数和角度偏差导数曲线如图6和图7所示。

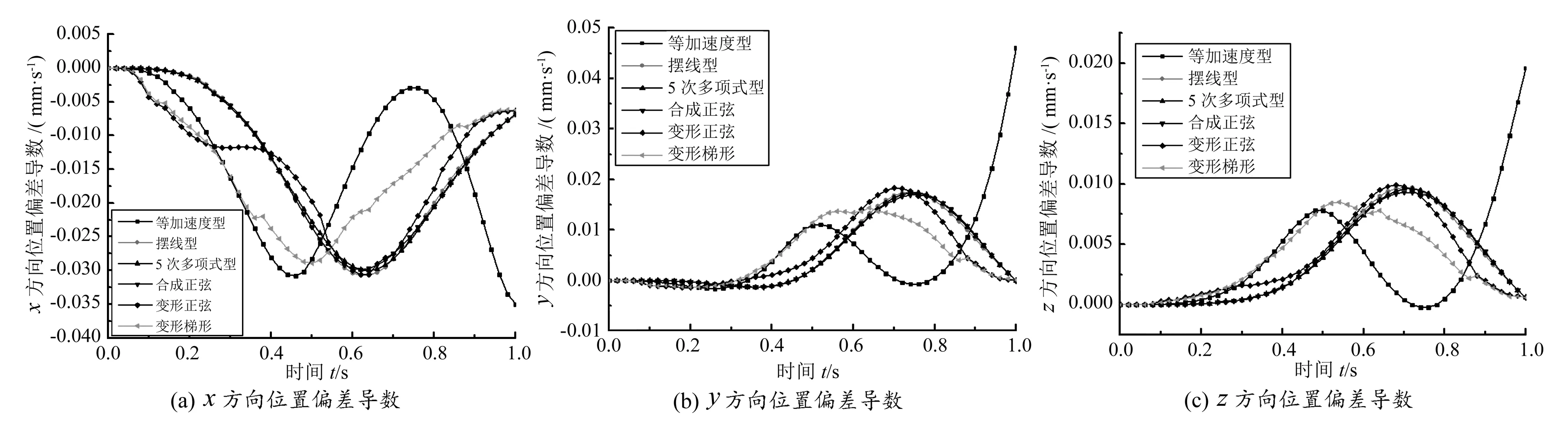
图6 不同加速度运动规律下ROV位置偏差导数

图7 不同加速度运动规律下ROV角度偏差导数

ROV位置偏差导数和角度偏差导数也可以理解为ROV受机械手运动影响产生的线速度和角速度。从图中可以看出，与其他几种运动方式相比，等加速度型方式下ROV位姿偏差导数曲线的波动程度较剧烈，t=1.0 s时位姿偏差导数与其他几种运动方式相比差异较大，ROV绝对位姿偏差导数最终值要远大于其他几种运动方式(见表6、表7)，说明当机械手停止运动时ROV仍保持较大运动速度，ROV位姿变化的稳定性受机械手运动影响较大。

变形梯形方式下ROV位姿偏差导数曲线不光滑，但曲线的波动程度较小。从表6、表7可以看出，绝对位置偏差导数最大值在x,y,z方向分别为0.028 9 mm/s、0.014 4 mm/s和0.008 5 mm/s，绕x,y,z轴转动的绝对角度偏差导数最大值分别为1.736 1(°)/s、0.522 9(°)/s和2.692 7(°)/s，要小于其他几种运动方式，绝对位置偏差导数最终值、绝对角度偏差导数最终值也比较小，说明在变形梯形方式下ROV位姿最平稳。

表6 不同加速度运动规律ROV绝对位置偏差导数统计数据

表7 不同加速度运动规律ROV绝对角度偏差统计数据

摆线型、5次多项式型和合成正弦方式下ROV位姿偏差导数曲线十分相近且光滑，从表6、表7可以看出,3种运动方式的绝对位姿偏差导数最终值比较接近，其中合成正弦方式下ROV绝对位置偏差导数最大值在x,y,z方向分别为0.029 9 mm/s、0.017 0 mm/s和0.009 3 mm/s，绕x,y,z轴转动的绝对角度偏差导数最大值分别为2.069 7 (°)/s、0.705 9(°)/s和3.248 1(°)/s，是3种运动方式下最小的，说明合成正弦方式下ROV位置偏差和角度偏差变化比较小。摆线型方式下ROV绝对位置偏差导数最大值和绝对角度偏差导数最大值略小于5次多项式方式，此运动方式下ROV位姿的平稳性好于5次多项式。

从表6、表7可以看出，变形正弦方式下绝对位置偏差导数最大值和绝对角度偏差导数最大值略大于摆线型、5次多项式型和合成正弦方式，但绝对位置偏差导数最终值和绝对位置偏差导数最终值要略小于这3种运动方式，说明机械手以合成正弦方式运动的过程中ROV位置偏差和角度偏差变化较剧烈，但对ROV最终位姿的影响却很小。

综合以上分析，从ROV位置偏差和角度偏差变化的平稳性考虑，变形梯形是比较好的选择，其次为合成正弦、摆线型和5次多项式型，再者是变形正弦，而等加速度型最差。

5 结束语

UVMS中机械手运动时会对ROV本体的位姿产生影响，机械手以不同的加速度运动方式完成同一动作时对ROV位姿的影响也不同。本文通过建立UVSM动力学模型，基于凸轮曲线理论进行仿真实验，研究分析了机械手以不同加速度运动方式运动时对ROV位置偏差和角度偏差的影响，研究成果对机械手运动误差补偿具有一定的参考价值。