基于COMSOL的超声导波检测锚杆锚固密实度研究

王云刚，邓万九，徐彦茹，刘春生

(1.河南理工大学 河南省瓦斯地质与瓦斯治理省部共建国家重点实验室培育基地，河南 焦作 454000;2.河南理工大学 煤炭安全生产河南省协同创新中心，河南 焦作454000;3.河南理工大学 安全科学与工程学院 河南 焦作 454000;4武汉长盛煤安科技有限公司 湖北 武汉 430000)

0 引 言

锚杆支护技术在煤矿、深基坑、隧道、边坡等工程领域被广泛应用，起到了良好的支护作用。锚固密实度是影响锚杆支护效果的重要因素之一，精准检测锚固密实度可判断锚杆的支护效果，为锚杆支护设计提供参考。

近年来，国内外学者提出利用超声导波检测技术对锚杆的锚固密实度进行检测。如M.D.Beard等[1]研究了L(0，1)模态超声导波在锚固锚杆中的传播，提出低频导波适合检测锚杆的锚固质量；YAN Z等[2]提出工程应用中应选用L(0，1)模态的导波检测锚杆的锚固质量，这样有利于反射波的提取和识别；廖霖等[3]对20～1 000 kHz导波频率内不同锚固质量的锚固锚杆进行了扫频，提出较低频率超声导波可用于锚杆锚固质量检测；何存富等[4-8]设计研制了锚杆超声导波检测仪器与检测系统，分析了超声导波在埋地锚杆中传播的特性，提出40～90 kHz的L(0，1)模态可用来对埋地锚杆进行检测；郭东辉等[9]定性分析了接收波列的波形特征、频谱特征、衰减特征与锚固质量之间的关系。何文等[10-12]对锚杆中的导波传播机理与锚固段上界面的反射波进行了研究，并试验了超声导波检测锚杆锚固密实度的可行性；吴斌等[13]分析了自由钢杆与置于土壤中钢杆的频散曲线，提出L(0，1)模态在低频段频散小、模态较少，在实际工程检测中可以选择40～90 kHz作为检测频率；王成等[14]等针对一种特定型号的端锚锚杆进行数值模拟，确定了不同频率激发波下有限元模型网格的最佳尺寸，得到该型号锚固锚杆质量检测的最佳激发波。目前，对于锚杆锚固质量的导波无损检测大多数为定性分析，定量检测分析研究较少。此外，利用超声导波探头在实验室进行测试时，要求较高，最佳测试频率和激发波不好确定，测试环境影响较大，测试结果比较单一，而利用数值模拟软件则可以方便地探究不同频率、不同测试条件下超声导波在锚杆中的传播规律。

基于此，本文利用COMSOL数值模拟软件对超声导波在锚固锚杆中的传播进行分析，研究低频超声纵向导波在不同锚固密实度锚杆的反射波波形图，推导超声导波在锚杆设计锚固段中传播时间与锚杆锚固密实度的关系，以期得到检测锚杆锚固密实度的定量分析方法。

1 超声导波检测原理

为换能器压电材料施加经汉宁窗调制的正弦函数脉冲电势，压电材料受到电信号影响产生超声振动，超声导波在锚杆中向锚杆末端传播。当传播到锚固界面时，由于介质结构改变，部分导波发生反射，经锚杆自由段传播至锚杆首端被换能器接收，另一部分导波发生透射，继续沿原来的传播方向在锚固段传播。当导波传播到锚杆末端时，大部分导波被反射，少部分导波发生透射，进入锚固介质。图1为检测锚固密实度的示意图。

图1 锚固密实度检测示意图

如果边界条件不同，波导特征频率发生变化，超声导波在锚杆自由段和锚固段中传播的群速度则不同。在较低频率条件下，超声导波在自由段中的群速度大于锚固段中的群速度[15]。锚固缺陷段的锚杆可看作周围没有锚固介质的自由段锚杆，超声导波从锚固段中传播到缺陷段时，群速度增加，与锚固密实度完整的情况相比，锚固密实度较差情况下，超声导波在设计锚固段L2中的传播时间将缩短，即超声导波在锚固界面的反射波与锚杆末端反射波的传播时间差t2缩短。假设超声导波在向前传播和经反射后传播的自由段锚固段速度不变,t2的计算表达式为

(1)

式中：t2为超声导波在设计锚固段L2中的传播时间，s；L2为设计锚固长度，m；L3为锚固缺陷长度，m；c1为超声导波在锚杆自由段中的群速度，m/s；c2为超声导波在锚杆锚固段中的群速度，m/s。

通过测量t2可求出锚固缺陷长度L3，进而根据式(2)求出锚固密实度D，

D=L2-L3/L2×100%。

(2)

根据《JGJ/T182-2009锚杆锚固质量无损检测技术规程》[16]，锚固质量可分为4个等级，如表1所示。

表1 锚固质量等级评价表

将式(1)转换成式(3)，L3为自变量，t2为因变量，t2随L3增加呈线性变化规律。不同频率的超声导波在锚固体锚杆中的传播速度不同，斜率也不同。

(3)

2 数值模拟及结果分析

2.1 锚杆模型建模

采用COMSOL结构力学固体力学模块，使用圆柱体模型对锚杆、超声换能器和周围锚固介质进行建模，利用不同圆柱体黏结长度模拟锚固长度，利用2个锚固段中间的缺陷长度模拟锚固缺陷长度，利用2个实际锚固段长度之和占设计锚固长度的百分比模拟锚固密实度，模型示意图如图2所示。

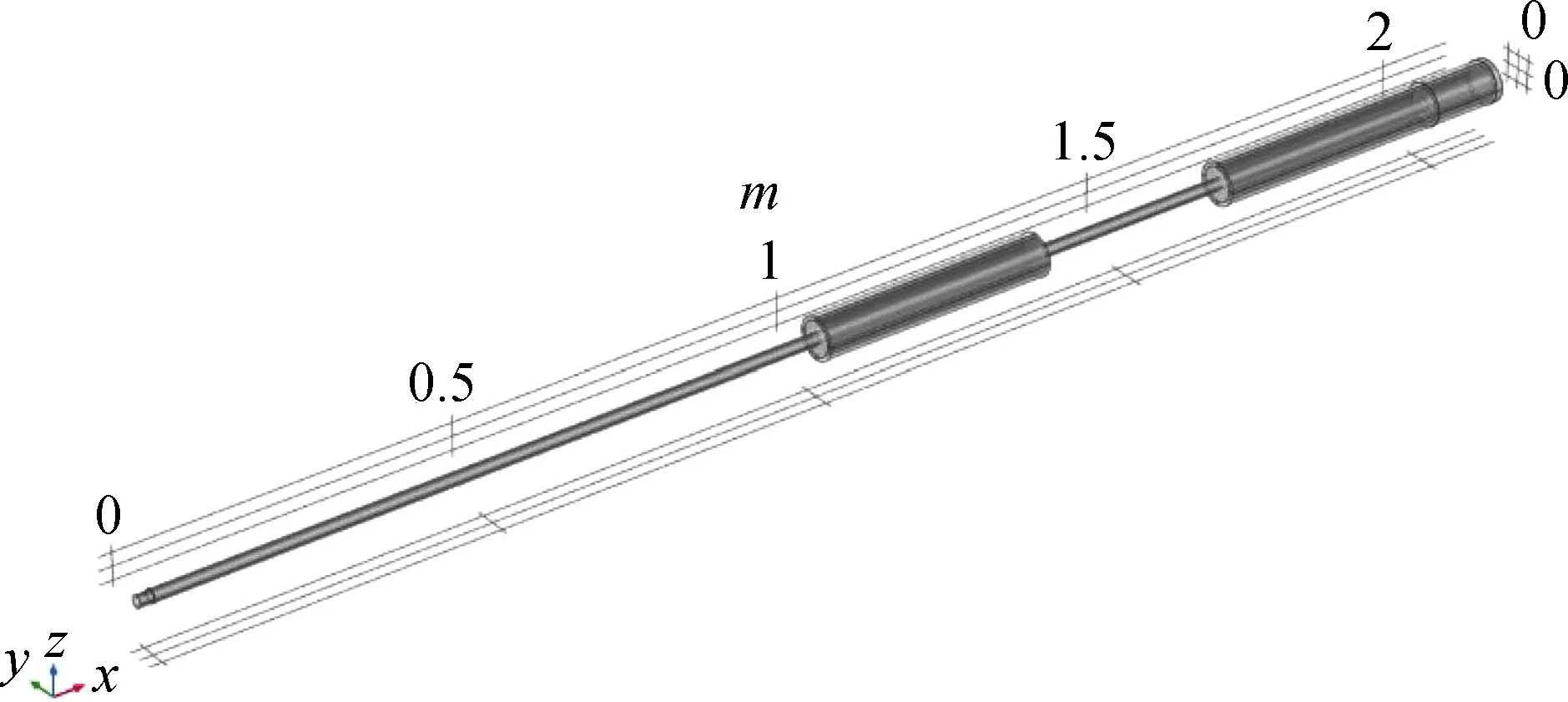
图2 锚固密实度模型

实际煤矿井下使用的锚杆长度多为2 m，因此本文锚杆模型长度L1设为2 m，直径20 mm，锚固段长度L2设为1 m，锚固缺陷L3长为0.1～0.9 m，步长0.1 m，为避免反射波叠加对波峰时间点读取的干扰，锚固缺陷设置在锚固段中间位置。几何模型中，为了模拟无限大介质，在锚固介质周围添加完美匹配层(PML)，锚杆模型采用结构钢，锚固介质和完美匹配层材料为混凝土，材料属性选自COMSOL内置材料库中的Structural steel和Concrete，结构钢弹性模量200 GPa，泊松比0.3，密度为7 850 kg/m3，混凝土弹性模量25 GPa，泊松比0.2，密度为2 300 kg/m3。

2.2 模态与频率选择

在圆柱和圆柱壳中传播的超声导波称为柱面导波。在杆中传播的超声导波存在3种模态[17]：纵向轴对称模态(L模态)、扭转模态(T模态)和弯曲模态(F模态)，由于T模态较难激励，故只考虑L模态和F模态，如图3所示。

从图3可以看出：(1)对于任意频率，都存在至少2种模态。F(1，2)，F(1，3)，L(0，2)模态均存在截止频率。90 kHz以下时，只存在L(0，1)和F(1，1)模态；(2)100 kHz以下，L(0，1)模态速度大于F(1，1)模态速度。随着频率增加，L(0，1)模态与F(1，1)模态之间的度差减少。

基于以上分析，选取L(0，1)模态导波进行模拟，该模态的轴向位移模式简单，易于激发；并选取50，60 kHz两个频率进行模拟。

图3 纵向、弯曲模态群速度曲线

2.3 模拟结果与分析

选取50，60 kHz两个频率,10个锚固密实度，共20组，由于模拟结果较多，且规律较相似，因此只给出了100%，90%，80%，40%锚固密实度的模拟结果波形图，分别代表表1中锚固质量等级的Ⅰ，Ⅱ，Ⅲ，Ⅳ，模拟结果如图4～5所示。

图4 50 kHz超声导波模拟结果

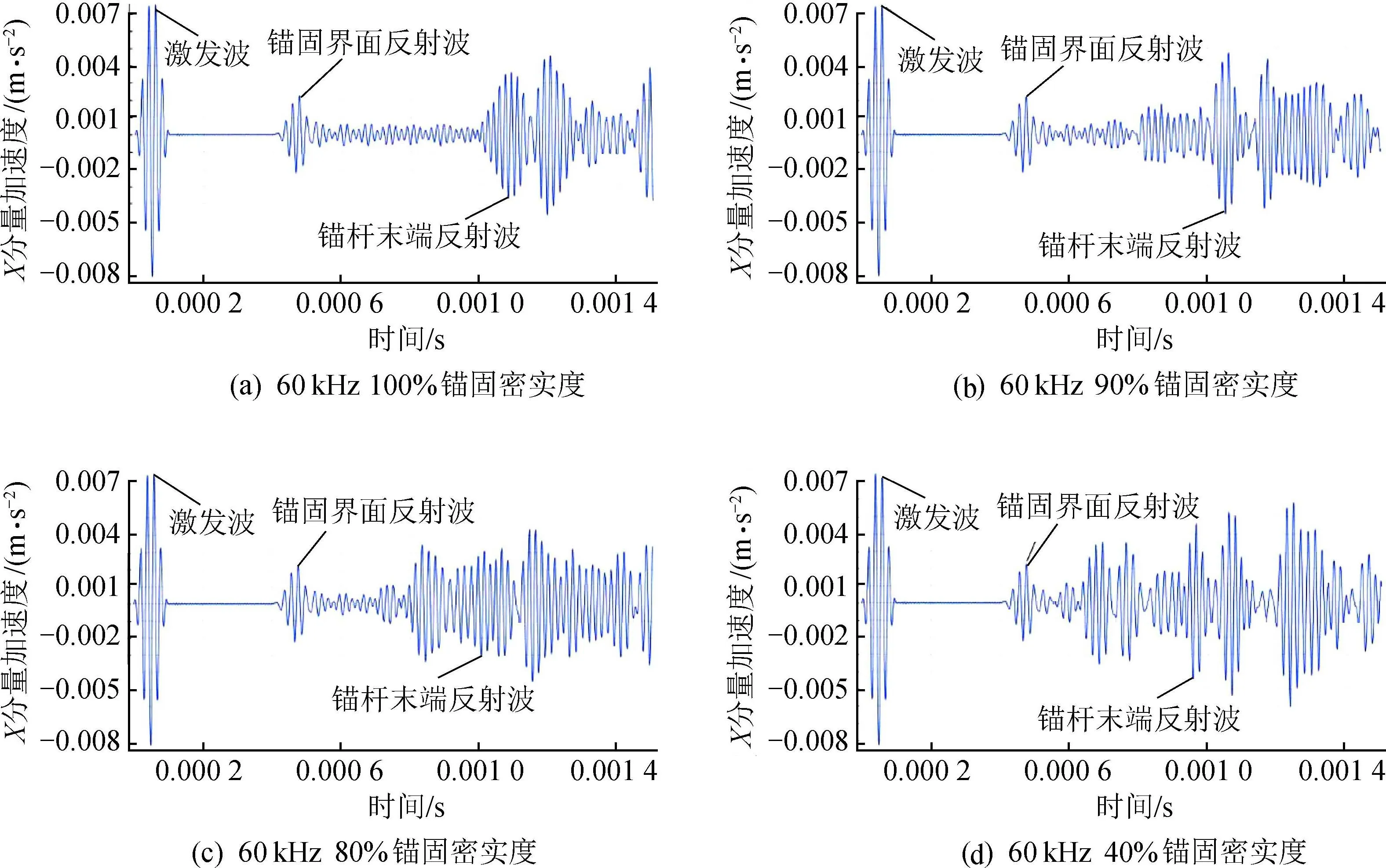
图5 60 kHz超声导波模拟结果

由图4可以看出，100%锚固密实度下，锚固界面反射波与锚杆末端反射波之间没有明显波峰，说明超声导波在这一段锚杆中传播时没有发生反射，且频散现象不明显。90%，80%，40%锚固密实度条件下，锚固界面反射波与锚杆末端反射波之间出现多个明显波峰，说明锚固段中存在锚固缺陷，超声导波在锚固缺陷界面上发生反射，这些反射波在其他界面也会发生反射，多个反射波叠加发生波形转换，因此锚固界面反射波与锚杆末端反射波之间的波形复杂；不同锚固密实度下，激发波和锚固界面反射波被接收的时间没有变化。锚杆末端反射波波形复杂，取首波波形最大处为锚杆末端反射波接收时间。由图4可以看出，锚杆末端反射波被接收的时间随着锚固密实度的降低逐渐减少。

由图5可知，60 kHz频率时，100%，90%锚固密实度下锚固界面反射波和锚杆末端反射波波峰明显，易辨别；80%，40%锚固密实度下锚杆末端反射波相对较平缓，但仍能辨别出波峰；随着锚固密实度降低，锚杆末端反射波被接收的时间逐渐减少，且锚固界面反射波接收时间略低于50 kHz频率下的接收时间、锚杆末端反射波接收时间高于50 kHz频率下的接收时间。

由图4～5可知，相同频率条件下，不同锚固密实度的模拟结果中，激发波和锚固界面反射波被接收的时间均未变化；不同频率下，锚杆末端反射波被接收的时间均随着锚固密实度的降低逐渐减少，说明锚固密实度越低，超声导波在锚杆设计锚固段中传播时间越短，表明锚杆末端反射波被接收的时间与锚固密实度之间相关性越好；不同频率、相同锚固密实度条件下，60 kHz频率的波形图相比于50 kHz频率下更加复杂。

将数值模拟结果数据导出，并计算超声导波在设计锚固段L2中的传播时间t2，汇总成表2。

表2 模拟结果汇总

随着锚固密实度降低，锚固缺陷长度增加，相同频率导波锚固界面反射波被接收时间相同，说明超声导波在锚杆自由段中群速度相同。10%锚固密实度时的2种频率导波锚固界面反射波接收时间与其他锚固密实度有差异，这是因为锚固缺陷较长，实际锚固段太短，导致第二个锚固界面的反射波与第一个锚固界面反射波相叠加，干扰了波峰时间点的读取；随着锚固密实度降低，锚杆末端反射波被接受的时间逐渐减小，t2也逐渐减小。将表2中锚固缺陷长度与t2的关系绘制成图，见图6。

将图6中不同频率条件下的数据分别进行线性拟合，从拟合结果中可以得出：频率50 kHz时，斜率为-148.1，截距为576.6，残差平方和为222.2，R2=0.99；频率60 kHz时，斜率为-177.3，截距为615.8，残差平方和为451.5，R2=0.98。可以看出，50 kHz频率下混凝土锚杆拟合优度大于60 kHz频率的，结合前文分析，50 kHz频率对于锚杆锚固缺陷长度检测误差更少。50，60 kHz频率拟合公式分别为式(4)～(5)。

t2=-148.1L3+576.6，

(4)

t2=-177.3L3+615.8。

(5)

图6 锚固缺陷长度与t2关系曲线

实际应用中，锚固密实度是检测目标，锚固缺陷长度L3是未知数，通过超声导波检测可以检测到导波在设计锚固段L2中的传播时间t2，因此将式(3)～(5)转换成式(6)～(8),

(6)

(7)

(8)

不同煤矿巷道的煤岩性质不同，设计的锚固长度、锚杆长度、锚杆材质等均不相同，这会导致超声导波在锚固锚杆中的群速度发生变化，因此，在实际应用中需根据实际情况做标定试验，测出导波在不同锚固密实度的锚杆中传播时间，然后根据式(6)得出经验公式，实际检测锚固密实度时,只需检测出超声导波在锚杆设计锚固段中的传播时间,即可得出锚固缺陷段的长度，根据式(2)求出锚杆的锚固密实度D，最后根据表1对锚杆的锚固质量进行分级评定。

3 结 论

(1)在50,60 kHz频率条件下，超声导波在锚杆设计锚固段中的传播时间与锚固缺陷长度均呈线性减小关系，并对该线性关系进行了线性拟合，提出用于实际检测的经验公式。

(2)对不同频率下相同锚固缺陷长度分析发现，60 kHz下的波形图较复杂，不利于数据的分析与提取；结合50,60 kHz下拟合直线拟合优度分析，提出50 kHz频率的拟合直线误差更小，更利于锚杆锚固长度检测。

(3)给出对锚杆的锚固质量进行分级评定的方法。只需在实际检测锚固密实度时，先进行标定试验，再检测出超声导波在锚杆设计锚固段中的传播时间,即可对锚固质量进行定量评价。