一种任意可靠度的修正滚动轴承寿命系数直接计算方法
王志阳,王文元,周红梅,李新华
(河南理工大学 机械与动力工程学院,河南 焦作 454000)
0 引 言
滚动轴承的失效主要包括疲劳破坏、过量的永久变形和磨损等。正常工作条件下,由疲劳点蚀引起的疲劳剥落是轴承失效的主要形式,因此,轴承的寿命一般是指疲劳寿命[1]。试验证明,滚动轴承的疲劳寿命是相当离散的,同一批生产的同一型号的轴承,在完全相同的条件下运转,其疲劳寿命各不相同,甚至相差数十倍,但它们的寿命却服从一定的概率分布规律。理论分析和试验表明,同一批类型的滚动轴承,在相同的试验条件下,其可靠度和寿命符合韦布尔分布。当可靠度小于90%时,滚动轴承的疲劳寿命符合两参数的韦布尔分布;当可靠度大于90%时,其疲劳寿命与三参数的韦布尔分布拟合得更好[2]。三参数韦布尔分布的位置参数是一正数,表明在此之前的可靠度为100%,这符合滚动轴承使用一段时间才开始出现故障的实际情况[3]。因此,国家标准[4]和ISO标准[5]以及各大轴承厂商对于可靠度大于90%的可靠度寿命修正系数都是以三参数的韦布尔分布制定的。但这些标准和轴承厂商的可靠度寿命系数都是离散化的系数(可靠度90%~99.95%时对应的离散修正寿命系数),如果求任意可靠度的滚动轴承寿命系数,当可靠度大于90%无法通过标准直接查表法获得时,需要用查表法结合线性差值的方法获得;而可靠度低于90%的轴承修正寿命系数则无法通过国家标准或ISO标准求出(可靠度低于90%时,国标和ISO标准没有给出修正寿命系数)。
滚动轴承的疲劳寿命用韦布尔模型表示是因为其疲劳寿命和一定深度的次表面裂纹有关[6]。对此,有许多学者进行了卓有成效的研究:潘光翔[7]采用三参数韦布尔分布参数估计方法对试验数据进行统计处理,得到不同载荷谱下载荷波动寿命修正系数,最终得到变载荷下滚动轴承疲劳寿命修正计算方法,为国产滚动轴承疲劳寿命预测评估提供了参考;冷钢[8]对比研究了二参数和三参数的韦布尔分布,对于高可靠度情况下,采用三参数韦布尔分布关系式的方法,得到的寿命修正系数要大于二参数方法;K.Pradeep等[9]提出了一种韦布尔加速寿命失效退化模型,该模型在韦布尔分布模型的基础上综合考虑了内部因素(如制造工艺、加工质量)和外部因素(如速度、负载、压力)对寿命的影响。但是,上述研究无法满足一些特定应用场合,需要计算任意可靠度的寿命或精确寿命的要求。为解决此问题,本文提出一种基于韦布尔分布的任意可靠度的滚动轴承寿命的直接计算方法。该方法统一了GB/T 6391-2010和ISO 281:2007标准的方法,而且可以求出低于90%可靠度的修正滚动轴承寿命系数。最后,用实例验证基于韦布尔分布的滚动轴承修正寿命系数直接计算方法的有效性。
1 任意可靠度的修正滚动轴承寿命系数计算方法
可靠度(reliability)定义为一组型号和测试条件相同时运转的滚动轴承期望达到或超过规定寿命的百分率,单个轴承的可靠度是该轴承达到或超过规定寿命的百分率。因此,可靠度也可以表示为幸存概率。如果幸存概率表示为R%,则失效概率表示为(1-R%)。可靠度为90%的滚动轴承寿命被称为基本额定寿命L10,任意可靠度(R≠0.9)的滚动轴承寿命计算也被称为修正额定寿命计算[10]。经长期实践证实,采用基本额定寿命L10作为轴承性能判据是令人满意的,该寿命与90%的可靠度、常用高质量材料、良好的加工质量和常规使用条件相关[11]。但在许多应用场合,人们开始希望计算不同可靠度的寿命或规定条件下更精确的寿命。研究发现,采用高质量的轴承钢,在良好的运转条件下并在低于某一赫兹滚动体接触应力下运转,如果不超过轴承钢的疲劳极限,轴承远长于L10的寿命。反之,在不良运转条件下,轴承寿命将低于L10寿命。大量的统计试验发现,在稳定不变的恒定负载下,滚动轴承寿命与可靠度关系符合韦布尔分布规律[9]。对于滚动轴承而言,三参数的韦布尔分布(轴承运行一段时间才发生故障)比两参数的韦布尔分布(t>0的任何时刻都可能发生故障)更能描述轴承的实际使用寿命。如果轴承寿命(L)用无量纲参量x=L/L10表示(L10为可靠度为90%的滚动轴承寿命),则三参数韦布尔分布如公式(1)所示[12],其韦布尔概率密度函数如图1所示。
(1)
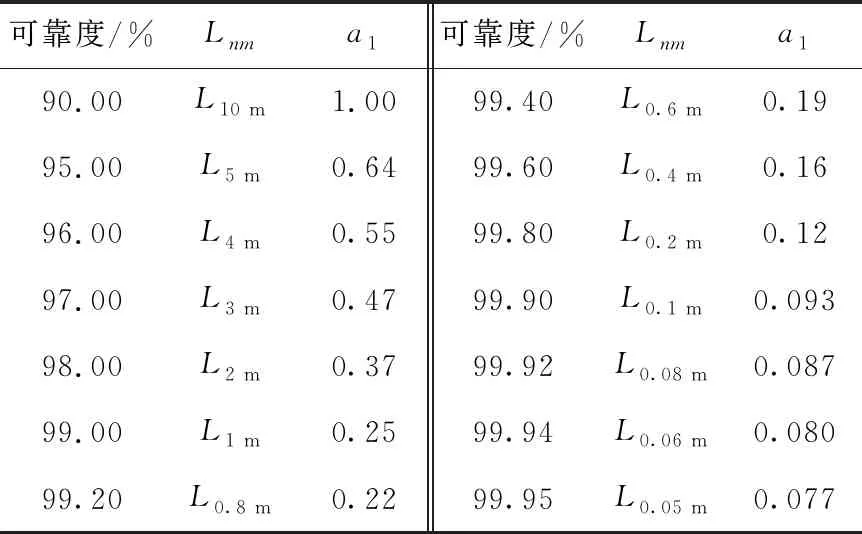
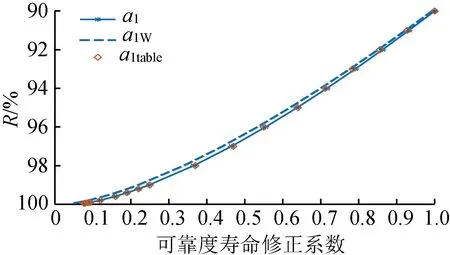
式中:R为可靠度;x为无量纲参量(L/L10);x0为位置参数,其物理意义为,当x 图1 韦布尔概率密度函数曲线 滚动轴承在某一可靠度下其无量纲寿命x(L/L10)的指数形式与负载F的乘积是一常数,如式(2)所示。这里a和k均为常数。该式对数形式是一直线(图2)。 Fxa=k。 (2) 图2 稳定可靠度图 滚动轴承在实际使用中的负载和转速经常与额定负载和额定转速(由轴承制造商的测试条件决定)不同,不同的使用环境和用途对可靠度的要求也不同。因此,根据工作载荷与转速以及需要的可靠度选择符合要求的滚动轴承,国标(或ISO标准)和设计手册都提供了一套行之有效的方案(表1),但该方法仅提供可靠度大于90%的修正寿命系统计算方法。本文提出一种稳定载荷下的任意稳定可靠度图(图2)计算方法,而非稳定载荷下的寿命系数计算则可以根据本文用分段近似稳定的方法得到。图2中,横坐标为无量纲寿命测度系数x,纵坐标为负载的对数,D点(负载为FD,可靠度为RD)为设计点,A点为轴承制造商给出的额定设计点(负载为额定负载C10,可靠度为90%)。根据设计要求,由D点到A点需要通过过渡点B(负载为额定负载C10,可靠度为RD)获得。首先,由D→B,满足同一可靠度下的式(2),因此有 (3) 从而可得 (4) 其次,由B→A,符合恒定负载下(C10)三参数的韦布尔分布规律,根据式(1),可得 (5) 由式(5)推导得 (6) 将式(6)带入式(4),同时注意到FB=C10,引入应用系数af(考虑轴承润滑、污染等因素对可靠性的影响),可得 (7) 式(7)即为滚动轴承在任意可靠度下和任意稳定负载(径向负载)下的轴承选用式(R<90%时)。根据式(7)中的基本额定动载荷C10,查找轴承制造商的产品目录就可以选择满足要求的滚动轴承。 式(7)中,括号内的分母部分写为 (8) 这里的a1就是可靠度寿命修正系数,是根据三参数(x0,θ,b)韦布尔分布所得。为了应用方便,根据泰勒级数,有 pf=1-RD。 式中的pf是失效概率(pf=1-RD)。因此式(8)可以用下式近似计算, (9) 表1 轴承修正额定寿命计算方法对比 国家标准(GB/T 6391-2010)、ISO标准(ISO281:2007)使用了式(8)变形形式, (10) 式中,S为国标和ISO标准中的百分比可靠度(R=S/100)。国标和ISO标准中的a1(式(10))是式(9)在参数时的形式。需要说明的是,为了计算方便,国家标准(GB/T 6391-2010)、ISO标准(ISO281:2007)、美国国家标准(ANSI/ABMA 9-2015)[13]以及主要的轴承制造商都对系数a1制成了表格(表2)和相应的计算方法(表1),不同的生产厂家和不同工艺水平可能有不同的参数。国家标准(GB/T 6391-2010)和ISO标准(ISO281:2007)为了兼顾到大多轴承制造厂的工艺条件和生产水平,给出的a1只是各种轴承类型和各生产厂家的最低值(可靠度±3σ下限的渐近线值)。但是,随着技术水平的进步和生产工艺的提高,韦布尔分布参数会发生变化,因此,ISO组织每5年会对其标准进行更新。另外,各大主要厂商一般都会给用户提供其个性化的韦布尔分布参数,这样可以得到更加精确的轴承寿命修正系数。因此,根据轴承制造厂提供的韦布尔分布参数和式(8)可以得到具体生产厂家更加精确的结果。 表2 可靠度寿命修正系数a1(GB/T 6391-2010) 图3为不同方法的寿命计算系数比较图。a1为公式(10)所得的结果;a1w是公式(9)在文献[14]中的结果(x0=0.02,θ=4.419,b=1.483);a1table是GB/T 6391-2010中的查表结果。由图3 图3 不同方法的可靠度寿命修正系数比较 可知,在同一可靠度下,a1w和a1table相比a1其值偏小,这说明公式法中的寿命修正系数是偏于保守的。由于a1table是根据式(10)可靠度的计算值,所以a1和a1table是重合一致的。另外,由ISO标准和机械设计手册[15]给出的系数是离散点,计算任意可靠度的寿命系数时需要利用线性插值的方法获得,此时线性插值方法所得的数值会略小于韦布尔函数方法(线性插值方法是偏于保守的,符合可靠性设计原则)。对于低于90%可靠度的滚动轴承寿命设计可以使用本文所提出的韦布尔分布函数或式(8)计算(两参数的韦布尔分布)。综上所述,基于韦布尔分布的寿命修正系数方法具有设计精度更高、逻辑清晰,适用面广的特点(可以应用于任意可靠度的滚动轴承修正寿命系数的计算)。 对式(7)做变形,可得 (10) 式(10)除了可计算给定负荷和轴承(基本额定动载荷)下的可靠度,还可以校核组合轴承(多轴承)的综合可靠度。 设计案例1现有一个受稳定径向负荷F=3 684.6 N的转轴两端欲安装一对同型号的深沟球滚动轴承,轴承应用系数为af=1.2,转轴速度为恒速n=300 r/min,滚动轴承要求工作时间不少于30万小时,综合可靠度为92%,根据上述条件选择滚动轴承。 问题分析:一对轴承的综合可靠度为92%,则单个轴承的可靠度为 无量纲参数xD=LD/L10=(60×30000×300)/106。 查表知[15],深沟球轴承的韦布尔参数x0=0.02,(θ-x0)=4.439,b=1.483,由式(7)得 C10=1.2×3 684.6× 查表GB/T 276-1994[15],应选内径为40 mm的6408型深沟球轴承。此时的修正寿命系数为 a1=0.02+4.439×(1-0.959)1/1.483=0.534 9。 如果用查表法计算(表2),由(0.95,0.64)和(0.96,0.55)可得线性插值后的可靠度寿命修正系数 a1表=0.55>a1=0.534 9, 查表法与三参数的公式法误差为 δ1=(0.55-0.534 9)/0.534 9=2.8%。 如果用二参数的韦布尔分布计算修正寿命系数,由式(8)得 a1二参数=4.459×(1-0.959)1/1.483=0.517 4, 查表法与二参数的公式法误差为 δ2=(0.55-0.5174)/0.5174×6.3%>δ1。 比较公式法和查表法的结果可知,对于可靠度大于90%的三参数公式法修正寿命系数略小于查表法,是偏于保守的。由二参数公式法所计算的结果与查表法的误差达到了6%左右,推荐使用查表法和三参数的公式法。 设计案例2对于设计案例1,现假设一对轴承的综合可靠度为80%,其他条件不变,选择合适的深沟球滚动轴承。 单个轴承的可靠度为 无量纲参数 xD=LD/L10=(60×30000×300)/106=540, 查表知[14],深沟球轴承的韦布尔参数x0=0,(θ-x0)=4.439,b=1.483,由公式(7)结合泰勒公式可得 C10=1.2×3684.6× 查表GB/T 276-1994[15],应选内径为35 mm的6407型深沟球轴承。此时的修正寿命系数为 a1=0.02+4.439×(1-0.89)1/1.483。 如果用查表法计算(见表2),由(0.90,1)和(0.95,0.64)可得线性插值后的可靠度寿命修正系数 a1表=1.07(>a1=1.02), 查表法与三参数的公式法误差为 δ1=(1.07-1.02)/1.07=4.7%。 如果用二参数的韦布尔分布计算修正寿命系数(此时式(9)中的x0为0),由式(9)得 a1二参数=4.459×(1-0.89)1/1.483 三参数方法与二参数方法的误差为 δ2=(1.07-1.03)/1.07=3.7%, 二参数和三参数的修正寿命系数误差为 δ3=(1.03-1.02)/1.03=0.97%。 比较上述结果可以发现,对于可靠度小于90%的滚动轴承寿命计算,查表法所得的结果误差较大,由二参数公式法所计算的结果与三参数公式法所得结果相差不大,这是因为它们的分布均符合韦布尔分布,差别仅在于初始位置参数的不同。因此,在计算可靠度低于90%的滚动轴承寿命时,国标GB/T 6391-2010和ISO 281:2007所提供的方法已不再适用,可以采用本文所提供的公式法(式(8)或(9))。 (1)滚动轴承的可靠度和寿命修正系数a1符合韦布尔分布。公式法(式(9))和查表法均可求得某一可靠度的寿命修正系数(R>90%)。公式法简洁、逻辑清晰,适用面广(可以求出任意可靠度的寿命修正系数);查表法方便、快捷,通用性好,可以满足高可靠度(大于90%的可靠度)的滚动轴承设计。 (2)公式法仅用韦布尔分布的三个参数即可描述滚动轴承任意可靠度(包括小于90%的可靠度)的寿命修正系数a1,其简洁的特性涵盖了国家标准和ISO标准的方法。企业可以发布自己的滚动轴承韦布尔分布参数,这种差异化的韦布尔参数有利于提高产品可靠性,推动滚动轴承企业之间的技术竞争和行业进步。


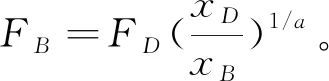

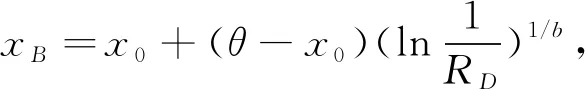
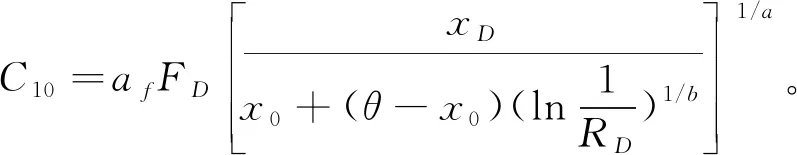

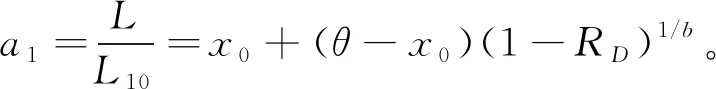



2 设计实例及分析
3 结 论

