高超声速飞行器气动伺服弹性的自适应抑制

朴敏楠，陈志刚，孙明玮,*，陈增强

1. 南开大学 人工智能学院，天津 300350 2. 空间物理重点实验室，北京 100076

吸气式高超声速飞行器(Air-Breathing Hypersonic Vehicle，AHV)被认为是能够经济可靠地实现太空探索与全球到达的重要手段，具有重要的军用和民用价值。2004年，X-43A AHV在马赫数为7和10的试飞试验中取得成功，这使得高超声速技术在近些年来重新成为科技界的研究热点。

不同于传统的飞行器，AHV采用机身与推力系统高度一体化设计、细长外形与轻质材料，这些使得AHV在气动、推力、弹性之间存在十分严重的耦合效应。此外，在整个飞行包络中，气动和环境参数变化范围很大且具有很强的不确定性。这些因素使得AHV的建模问题十分复杂且面向控制的模型存在很强的不确定性。针对弹性AHV的强耦合效应和各种不确定性带来的控制问题，已有很多学者开展了研究，提出了基于自适应控制、滑模控制、神经网络控制、自抗扰控制等方法的诸多控制方案[1-9]。这些控制方法仅考虑了气动弹性问题，即AHV的结构动力学和非定常气动力之间的交互作用。除了气动弹性问题，控制系统设计还需要考虑传感器测量信号包含的弹性振动通过控制器反馈对整个闭环系统的影响，即气动伺服弹性(Aeroservoelasticity，ASE)问题。AHV的ASE抑制主要有两个难点：一是其弹性频率随着燃油消耗和气动加热在整个飞行包络内有较大的变化范围；二是其低阶弹性频率较低，刚体控制性能与低阶弹性模态抑制之间相互冲突，尤其对于具有静不稳特性的AHV[10]。针对这两个问题，自适应陷波器(Adaptive Notch Filter，ANF)是一种有效的解决方法。ANF可以通过实时的频率辨识滤除测量信号中的弹性振动从而实现弹性模态的幅值稳定，并且其窄陷波带宽可以降低对刚体控制性能的影响。

根据ASE抑制问题的特点，提炼出ANF的关键性能需求如下：

1) 只需用到速率陀螺测量信号，不需要刚体模型信息。这样可以降低辨识算法复杂度以及刚体建模误差对辨识结果的影响。

2) 能够进行多个弹性频率的直接辨识。传统ANF设计采用频率间接辨识方案，需要基于多项式系数进行在线因式分解得到频率估计。当弹性频率多于两个时，高阶多项式因式分解的计算复杂度较高且因式分解结果对多项式系数的微小摄动非常敏感。而频率直接辨识方案无需在线进行高阶多项式的因式分解，这样能够避免间接辨识带来的上述问题。

3) 具有较快的收敛速度和较高的辨识精度，能够快速有效地抑制弹性模态。

4) 当系统中的弹性振动能量较低，即振动信号的信噪比(Signal-to-Noise Ratio，SNR)较低时，辨识算法仍需要具有收敛性。

5) 随着AHV飞行工况以及结构动力学的变化，各阶弹性模态的能量也在不断发生变化。辨识算法需要能够精确地区分多个能量相近的弹性模态，并且对各阶弹性模态的能量变化具有较强的鲁棒性。

国内外学者针对ANF在AHV、防空导弹、运载火箭等对象上的应用性研究已经取得了很多成果[11-19]。然而，这些研究设计的ANF都只具有上述一个或者某几个特点，不能够综合满足多个需求。文献[11-14]的ANF设计需要刚弹模型参数的联合辨识，增加辨识难度的同时降低了辨识结果的可靠性。文献[15-19]在频率间接辨识框架下采用SMM(Steiglitz-Mcbride Method)实现对一个或者两个频率的辨识，但是在针对3个及以上弹性频率时仍存在间接辨识的诸多弊端。因此，探索满足上述多种要求的ANF设计方法是十分必要的。

基于上述对控制问题和需求的分析，本文提出一种实用的AHV气动伺服弹性控制方案。针对强耦合和强不确定性问题，采用线性自抗扰控制(Linear Active Disturbance Rejection Control，LADRC)[20-21]。通过将所有异于串联积分型的动态视为总扰动，并采用扩张状态观测器(Extended State Observer，ESO)进行估计，可以以一种简单高效的方式处理强耦合与不确定性[22-23]。对于ASE抑制问题，本文针对上述总结的性能要求，从辨识框架、辨识算法和在线有效性监督3个角度研究了面向实用的ANF设计方法。首先，ANF的设计仅需采用速率陀螺信号即需求1)。其次，为了实现频率直接辨识，设计、分析和对比了两种方案，参数单独自适应(Individual Adaptation，IA)方案和同步自适应(Simultaneous Adaptation，SA)方案[24]即需求2)。在辨识算法上，基于有些学者对随机高斯牛顿法(Stochastic Gauss-Newton，SGN)、递推最大似然法(Recursive Maximum Likelihood，RML)、近似最大似然法(Approximate Maximum Likelihood，AML)和近似梯度法(Approximate Gradient Based，AGB)在性能上的比较研究[25]，本文选择收敛速度和辨识精度综合性能更好的RML作为辨识算法(需求3)。虽然SMM算法近些年来在ANF上得到了很多研究[15-19]，但是其在两种频率直接辨识框架下的性能相比于RML并不优越。针对需求4)和5)，本文设计出一种能够显著增强辨识算法在低信噪比和变化飞行工况下鲁棒性的在线有效性监督机制。通过对上述问题的研究，本文对AHV的ASE抑制问题提供了一个考虑更多实际因素的综合解决方案。

1 模型介绍

本文选择文献[26]中的弹性AHV模型作为研究对象。文献[26]将弹性AHV建模为自由梁，使得刚体模态与弹性模态之间满足正交性，即刚体与弹性模态之间仅通过力和力矩的作用相互影响。考虑到鸭翼的引入不仅能够改善弹道倾角动态特性而且有助于镇定弹性模态，该模型中还引入了鸭翼控制量。该模型如下：

(1)

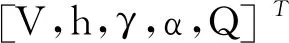
(2)

(3)

表1 随燃油水平变化的弹性频率Table 1 Elastic frequencies for different fuel levels

式(3)中各气动系数的取值详见文献[26]。该AHV的几何外形如图2所示，其中θm表示附加的弹性俯仰角。

在实际情况中，角度和角速度测量量不仅包含刚体运动信息，还包括与传感器安装位置有关的各阶弹性振动信息。设该弹性AHV的前三阶弹性振型分别为φ1(l)、φ2(l)和φ3(l)，其中l表示沿飞行器轴纵与机头之间的距离。速率陀螺安装在飞行器的lrg处，则速率陀螺测量到的俯仰角速度和相应的俯仰角为

(4)

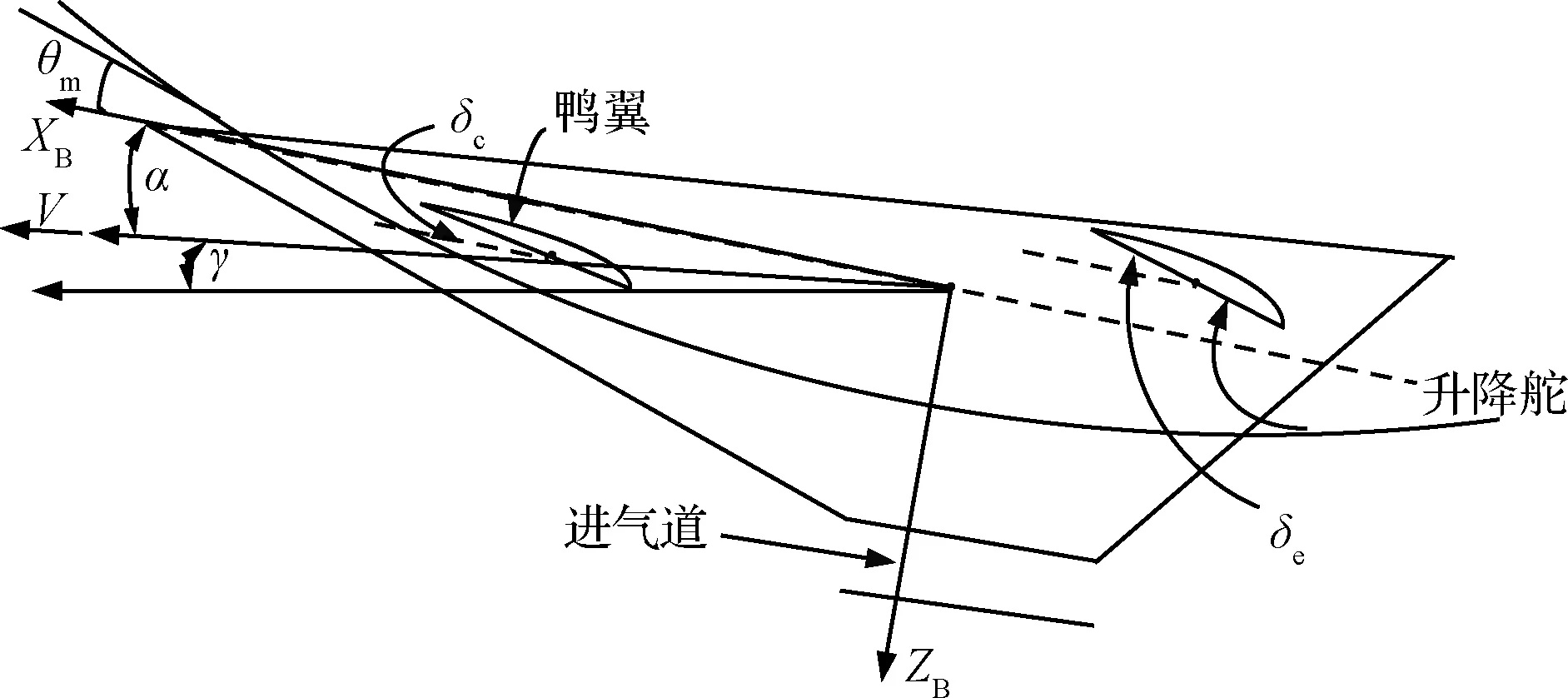
图2 弹性AHV的几何外形Fig.2 Geometry of flexible AHV

2 姿态控制器设计

为处理弹性AHV的强耦合和强不确定性，姿态控制器设计采用的是LADRC。首先建立被控量俯仰角与控制舵偏之间的标准型——串联积分型，然后将所有异于标准型的部分视为总扰动并设计ESO对其进行估计，最后在控制量中通过总扰动估计直接对总扰动进行补偿。首先为了消除升降舵对升力的影响带来的弹道倾角非最小相位特性，将鸭翼和升降舵之间按照

(5)

进行配置。将式(2)和式(3)代入到式(1)中的姿态角运动方程得到

(6)

将式(6)写为

(7)

其中:

(8)

其中：aδe为稳态控制增益；fθ为俯仰角通道的总扰动，其中包括了推力、弹性效应对俯仰力矩的影响、参数不确定性、未建模动态以及可能受到的各种外扰。下面对式(7)设计降阶ESO

(9)

其中：w为辅助变量；z2为总扰动估计值;ωo为文献[21]提出的观测器带宽。ωo在自抗扰控制中是一个非常关键的参数，其选择需要综合考虑扰动抑制能力以及稳定裕度。在得到总扰动的估计后，可以设计带有扰动补偿和误差反馈的综合控制输入

(10)

式中：θc为俯仰角指令；kp和kd分别为比例和微分控制增益。令Qp和θp分别表示测量信号经过ANF的俯仰角速度和俯仰角输出，即

(11)

(12)

整个控制系统的框图如图3所示。

图3 姿态闭环控制系统框图Fig.3 Diagram of the closed-loop attitude control system

3 ANF设计

频率直接辨识可以通过IA和SA两种框架实现，这两种框架的参数更新方式如图4所示。在IA框架下，ANF可以视为多个二阶ANF的串联，每个ANF只辨识一个弹性频率，且参数更新仅基于局部的输入输出数据。而在SA框架下，所有的频率估计都基于测量信号和最终的滤波器输出同时进行更新。本文选用文献中使用最为广泛的零极点受限ANF模型[27]

(13)

图4 两种频率直接辨识框架Fig.4 Two schemes for the direct estimation of frequency

3.1 IA型ANF设计

IA框架下，每个ANF待优化的目标函数为

(14)

式中：λ为遗忘因子；Ns为数据长度。每个ANF基于RML[27]的频率估计算法流程如下：

1) 预测误差计算

(15)

2) 梯度计算

令ψi(k)=-∂ei(k)/∂ai可以得到

ψi(k)=-ai(k-1)ρ(k)ψi(k-1)-ρ2(k)·

(16)

3) 参数更新

根据预测误差和参数梯度可以得到参数的更新式为

(17)

ai(k)=ai(k-1)+Pi(k)ψi(k)ei(k)

(18)

对于每个ANF，只有一个待辨识参数ai，因此式(17)可以简化为

(19)

4) 后验误差计算

(20)

5) 设计参数更新

为了提高算法的收敛速度，为ρ和λ设计过渡过程

(21)

式中：ρs和λs为期望的稳态值；ρw和λw为过渡过程时间常数。

6) 频率计算

ωi(k)=arccos(-ai(k)/2)/ts

(22)

由于该框架直接对ai进行更新，因此需要在线进行如下的稳定性监测

(23)

这种串联式估计框架存在以下几个特点：

1)H1(z-1)具有最高的优先权选择一个收敛频率。随着序列号的增加，ANF的优先权依次递减。序列号高的ANF只有当前面的ANF收敛之后才能够收敛。因此，可以经常观察到高序列号ANF的频率辨识结果呈阶梯状且收敛速率较慢。

2) 由于估计算法基于目标函数式(14)，具有更高能量的频率会被ANF优先估计。

3) 在自适应算法的开始阶段，几个ANF可能会同时估计某一个频率直到其中一个ANF首先收敛到这个频率并使得相应的弹性振动信号能量衰减到很小。这是因为每个ANF都是基于局部的误差信息进行参数更新的，因此这种框架会导致一个较低的收敛速率并且整体最优性难以得到保证。

3.2 SA型ANF设计

SA框架下自适应辨识算法待优化的目标函数为

(24)

其基于RML的频率估计算法流程[29]和IA框架相似，具体步骤如下：

1) 预测误差计算

(1-ρ2(k))Zi(k-2)+xi(k)

(25)

式中：x1(k)=x(k)，xi(k)=ei-1(k)(i=2,3,…,N)，Zi为根据k时刻最新参数估计得到的ANF中间状态。

2) 梯度计算

(26)

可以得到

(27)

其中

(28)

联合式(27)和式(28)可以得到

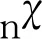
(29)

其中

(30)

可以看出所有梯度的计算都用到了最终误差估计e(k)。

3) 参数更新

定义梯度向量和参数向量

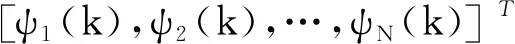
(31)

(32)

则参数更新公式为

(33)

(34)

4) 后验误差和中间状态计算

基于最新参数估计计算后验误差和ANF的中间状态

(35)

5) 设计参数更新

(36)

3.3 性能比较

该部分通过3种情形下的数值仿真说明2种算法的特点以及当存在测量噪声时进行在线监督的必要性和有效性。ANF输入信号的形式为

(37)

表2 3种情形下的参数设置Table 2 Design of parameters for three cases

图5 情形1下的频率估计Fig.5 Frequency estimation for case 1

在ASE抑制问题中，ANF的输入信号包含测量噪声且是复杂多变的。当系统中的弹性振动能量较低，即振动信号信噪比较低时，辨识算法的收敛性很难得到保证。随着AHV飞行工况以及结构动力学的变化，辨识算法需要对各阶弹性模态的能量(振动幅值)变化具有较强的鲁棒性。因此，为了保证算法可靠性，本文设计了一种基于弹性频率先验知识的在线有效性监督机制。令

(38)

(39)

这样可以对辨识结果进行及时的在线纠正，保证自适应算法在合理的范围内进行搜索并使得参数估计最终收敛到真值。下面考虑存在噪声时频率不变和时变两种情形，情形2下的频率同情形1，情形3下的频率分别为ω1=10+t，ω2=40+1.5t，ω3=80+6t。在不同SNR下，两种算法在以上两种输入信号下运行100次，并统计100次运行结果的估计偏差标准差DIA和DSA，如表3 和表4所示。当存在白噪声且没有式(39)中的有效性监督时，两种算法在多次仿真中都有一个或者多个频率不能够收敛到真值。加上在线监督后，每次仿真结果中的所有频率都会收敛到真值。由此可见，本文设计的监督策略会增强SA对初始设计参数的鲁棒性。从表3和表4可以看出，SA框架具有更高的辨识精度。因此，SA框架通过在线监督鲁棒性得到提高后，其相较于IA框架具有更好的频率辨识性能。

表3 不同信噪比下两种框架的估计标准差(情形2)

表4 不同信噪比下两种框架的估计标准差(情形3)

4 仿真结果

4.1 非线性仿真

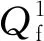
(40)

其中

u=δer

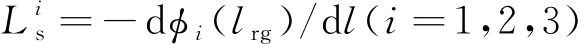
(41)

图6 自适应陷波器在50%燃油水平下的伯德图Fig.6 Bode plot of ANF for 50% fuel level

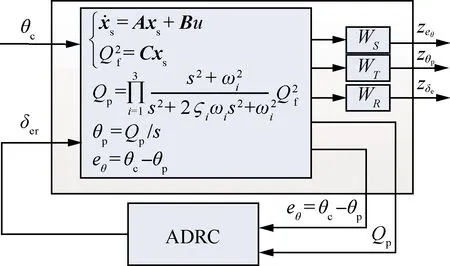
图7 控制器参数优化框图Fig.7 Block diagram for controller parameter optimization

(42)

通过观察优化结果是否满足气动伺服弹性抑制和鲁棒性要求来适当地调整权重函数，最终得到满足多个要求的控制参数。权重函数的选择详见文献[10]。可以看出上述优化过程综合考虑了飞行器本体刚弹特性以及滤波器的特性。

假设各阶弹性频率随燃油消耗以线性形式变化，变化范围覆盖表1。当弹性阻尼ζi=0.02时，仿真结果如图8～图13所示。图8显示了经过ANF滤波后的弹性俯仰角响应，可以看出弹性振动经过20 s的抑制之后衰减显著。控制舵偏量如图9所示。为了进一步分析弹性振动的抑制情况，将弹性俯仰角速度信号在仿真时间内分为3个阶段P1(0～20 s)、P2(20～50 s)和P3(50～120 s)进行离散傅立叶变换，变换结果如图10所示。从图10可以看出，各阶弹性振动的能量在不同阶段有所变化。在P1阶段，三阶模态能量最强，在P2阶段，三阶模态得到了显著抑制，一、二阶模态能量相对较强，在P3阶段，前三阶弹性振动都已基本滤除干净。弹性频率估计结果如图11所示，可以看出3个辨识频率在1 s左右收敛到真值附近，具有较快的辨识速度。由于各阶弹性模态都得到了及时有效的抑制，系统能够稳定运行。在20 s之后，三阶弹性频率估计出现了较大的波动。这个波动的产生主要有两个原因。一是在这个阶段三阶弹性俯仰角速度不是广义正弦信号(幅值和频率时变的正弦信号)，其不止在三阶频率点处有能量，还在其他频率处有能量。这可以从图12及其局部放大图13中看出。由于弹性模态阻尼非零且各阶弹性模态之间存在耦合作用，某些飞行工况下弹性振动信号不只是在某个频率点处有能量。由于一二阶弹性俯仰角速度还保持广义正弦信号形式，所以估计不存在较大的波动。第2个原因是随着弹性模态逐渐被抑制，弹性振动信号的SNR逐渐降低，在P2阶段，三阶模态的SNR最低，这也会导致估计值出现较大的波动。这些实际因素都说明了AHV的>ASE抑制问题更为复杂，必须进行在线有效性监督以保证其可靠性。作为对比，不加监测机制的仿真结果如图14和图15所示。由于三阶频率辨识收敛较慢(1.8 s左右)且二阶频率辨识错误地收敛到一阶频率，产生了弹性振动反馈导致的控制量饱和以及不稳定飞行器的失稳。将弹性模态阻尼减小至ζi=0.004，这样可以使得弹性振动信号更接近于广义正弦信号，此时频率辨识结果如图16所示，可以看到波动几乎消失，这也验证了上述分析结果的正确性。

图8 俯仰角响应Fig.8 Pitch angle response

图9 控制舵偏Fig.9 Control deflections

图10 弹性俯仰角速度信号的离散傅立叶变换Fig.10 DFT of flexible pitch angular rate signal

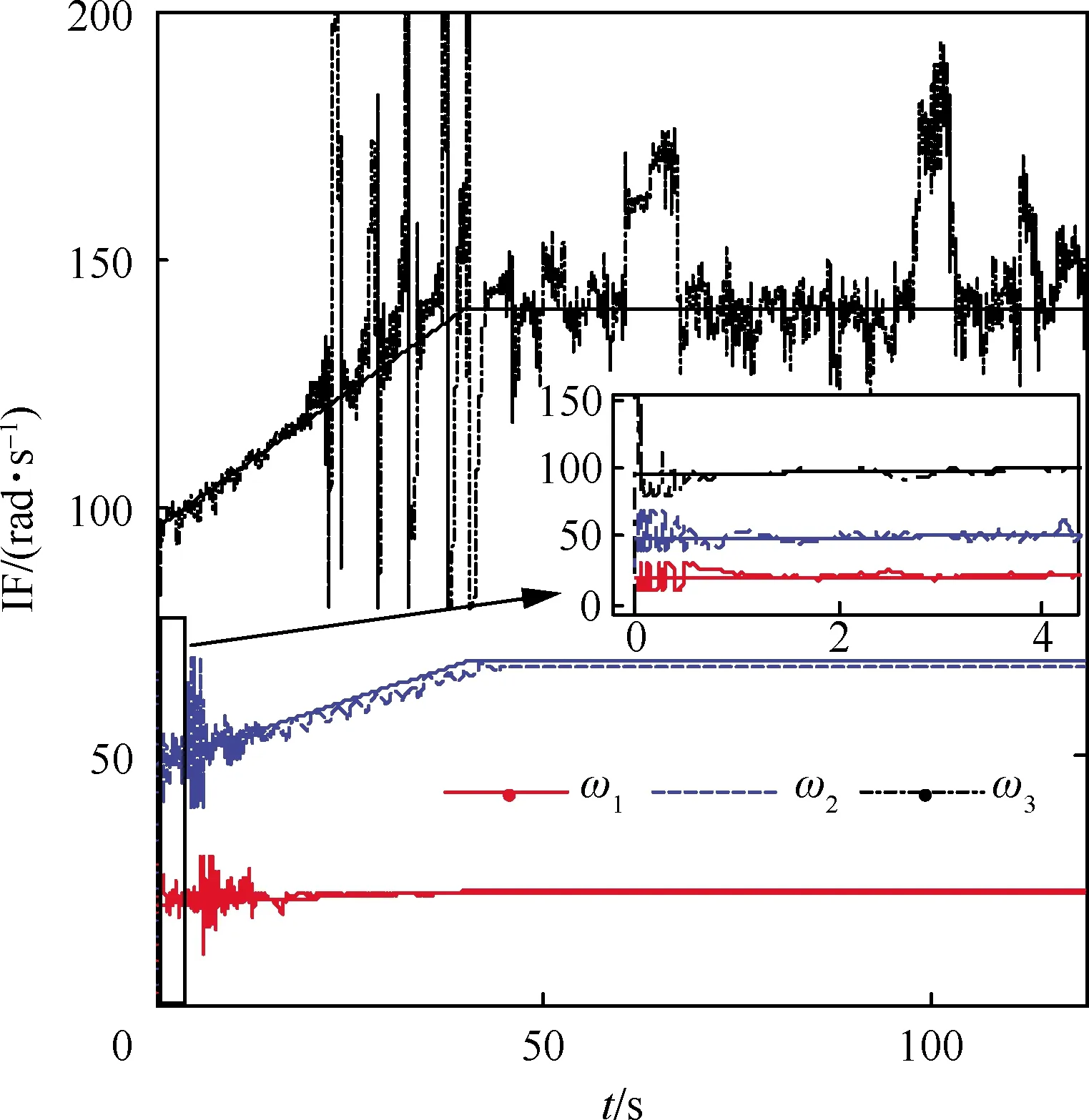
图11 各阶弹性模态的频率估计Fig.11 Frequency estimation of flexible mode

图12 弹性俯仰角速度Fig.12 Flexible pitch angular rate

图13 弹性俯仰角速度20 s左右局部放大图Fig.13 Flexible pitch angular rate around 20 s

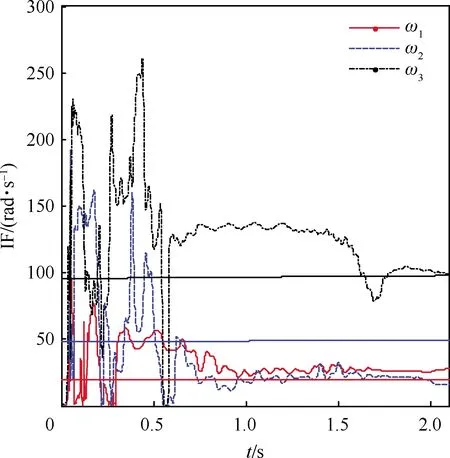
图14 不加监测时的频率估计Fig.14 Frequency estimation without monitoring

图15 不加监测时的俯仰角响应Fig.15 Pitch angle response without online monitoring

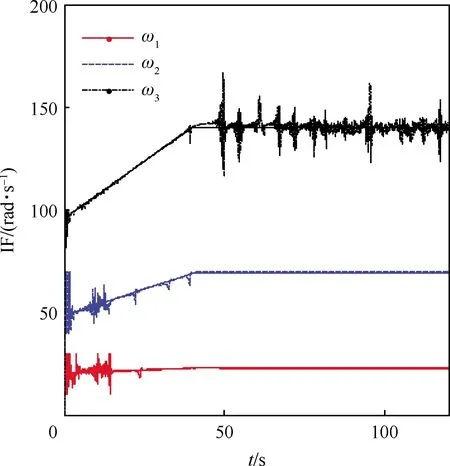
图16 ζi=0.004时各阶弹性模态的频率估计Fig.16 Frequency estimation of flexible mode for ζi=0.004

4.2 定点对比分析

鲁棒控制解决ASE问题的机理和幅值稳定比较相似，主要通过在控制器中进行关键弹性模态的幅值衰减，因此文中选择鲁棒控制作为新的弹性控制对比方法。鲁棒控制是一种基于对象线性模型的方法，在整个飞行包络内同时考虑气动参数、结构参数时变和不确定性的鲁棒控制器设计本身就是一个较为复杂的研究问题，需要进行控制器参数调度。因为本文重点关注ASE抑制问题，所以在只考虑弹性频率不确定性条件下(各弹性频率摄动范围如表1所示)选择一个特征点进行鲁棒控制器设计。

(43)

图17 弹性俯仰角频率响应的乘性不确定性Fig.17 Multiplicative uncertainty of frequency response of flexible pitch angle

图18 鲁棒控制弹性俯仰角阶跃响应Fig.18 Step response of flexible pitch angle for robust control

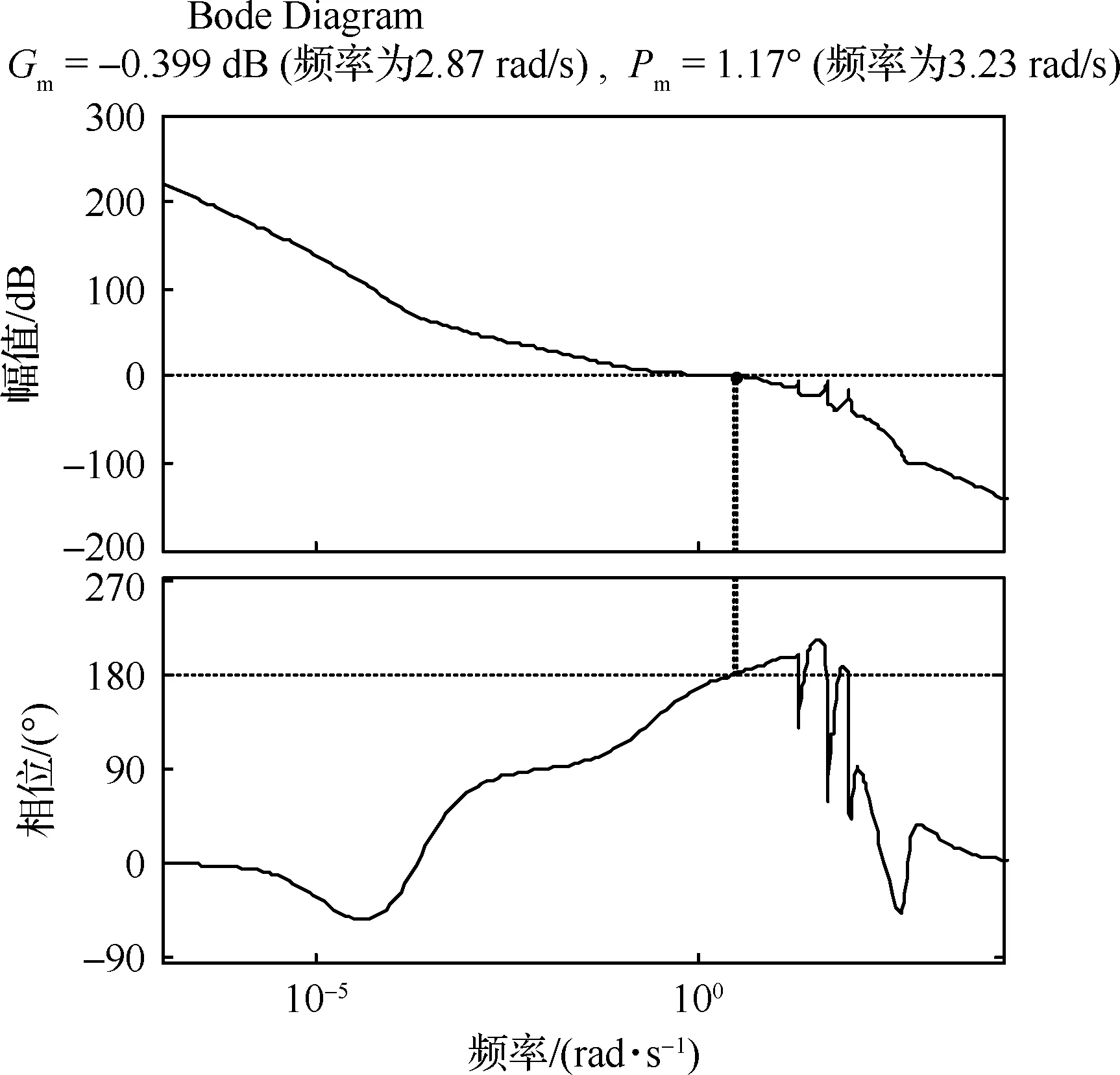
图19 鲁棒控制回路传递函数Fig.19 Loop transfer function for robust control

在该特征点处同样进行本文控制方案的性能分析，假设ANF的频率估计准确，阶跃响应结果和回路传递函数如图20和图21所示。由于ANF的自适应能力，陷波宽度可以设计得较窄，在保证响应速度和弹性频率处衰减程度的前提下稳定裕度得到了提升，为(4.45 dB，21.3°)，因此本文方案能够在保证ASE抑制能力的前提下一定程度上提高系统的鲁棒性。

图20 本文控制方案弹性俯仰角阶跃响应Fig.20 Step response of the flexible pitch angle for proposed method

图21 本文控制方案回路传递函数Fig.21 Loop transfer function for proposed method

5 结 论

1) 将LADRC和ANF结合在一起既能够处理强耦合和强不确定性，又能够对频率时变的弹性振动进行抑制。由于ANF的陷波带宽较窄，可以最大程度减小对刚体控制效果的影响。此外，整个控制系统的线性形式也便于进行工程上的频域分析。

2) IA和SA框架在实现多频率直接辨识时各有利弊。IA框架的收敛速度和辨识精度差于SA，但是对ANF设计参数以及信号幅值变化的鲁棒性更强。当加上在线监督机制后，SA对设计参数以及信号幅值变化的鲁棒性可以显著提升，此时其综合性能更优于IA框架。

3) 实际弹性振动信号复杂多变，可能不是广义正弦信号的叠加，且受到测量噪声的影响，因此，对频率辨识结果的在线有效性监督是必须的。