TSTO运载器一级返场轨迹优化设计与在线生成

张柔和，樊雅卓，佘智勇，崔乃刚,*

1. 哈尔滨工业大学 航天学院，哈尔滨 150001 2. 北京空天技术研究所，北京 100074

空天飞行器是未来实现快速低成本往返空间的重要工具之一，其发展存在多种可能的技术路线。美国的国家空天飞机计划[1]、德国的桑格尔计划[2]、英国的云霄塔计划[3]是其中的典型代表。水平起降两级入轨(Two Stage To Orbit, TSTO)运载器是空天飞行器一个重要的发展方向。TSTO运载器研究历程久，发展路径清晰，相比单级入轨运载器技术跨度小，在材料科学和推进系统快速发展的推动下具有突出的工程实现潜力。20世纪末以来，美国开展了多个TSTO运载器项目和概念研究[4-8]。中国正在开展的腾云工程也是TSTO运载器的典型代表。

轨迹优化设计是总体设计阶段的重要环节，对飞行器总体方案论证、总体性能提升具有重要意义。目前针对TSTO运载器的轨迹优化问题研究主要集中在组合体和二子级上升段，大多以燃料最省、起飞规模最小等作为指标进行优化设计[9-14]，而对于一子级返场问题鲜有关注。

TSTO一子级返场轨迹设计属于临近空间再入轨迹设计问题。现有再入轨迹设计方法大多针对总体规模较小、升阻比2～3左右的升力体飞行器提出，其初始速度较大(通常马赫数为15以上)、初始高度较高(通常为60 km以上)[15-19]。而一子级返场轨迹与典型的空间/临近空间再入轨迹具有显著区别。首先，分离时刻一子级需负担的重力瞬间减小，导致分离后一子级面临升力过剩问题。其次，一子级返场过程存在大幅转向需求，而一般再入问题的初始航向偏差较小。此外，一子级大尺寸、大惯量的机体导致倾侧角多次翻转存在困难，难以采用典型升力式再入飞行器的倾侧角翻转逻辑。最后，一子级外形兼顾高速和低速性能，在宽域范围内气动特性变化显著[20]。上述特点对如何设计轨迹从而兼顾转向需求、可实现性和光滑平稳特性提出了挑战。

一子级返场面临的另一个突出问题是组合体分离存在明显的分离扰动，其过程机理复杂、模拟困难[21]。分离扰动将显著影响飞行器状态，造成一子级返场初始状态与标称状态存在较大偏差。因此，需要解决大初始偏差条件下一子级返场轨迹在线生成问题。

王志刚等[22]采用最优控制理论对大回转轨迹开展研究，但轨迹无法保证光滑平稳且求解困难。梅映雪等[23]设计了考虑禁飞区和测控区的分段优化策略，对复杂约束问题提供了解决思路，但设计的轨迹需要倾侧角快速、多次翻转。以Shen和Lu提出的拟平衡滑翔[15]为代表的在线轨迹生成方法主要关注小尺寸的高超声速飞行器再入问题，需要倾侧角多次翻转，难以应用于本文对象。陈万春等给出的拟平稳滑翔弹道解析计算方法[24]具有在线计算潜力，但其航迹角单调变化的假设不适用于一子级返场轨迹问题。Jorris和Cobb[25]采用最优控制思想求解了再入轨迹，但难以满足一子级返场光滑平稳需求。Zhang等[26]结合阻力加速度剖面和传统的航向角误差走廊进行轨迹规划，实现了对禁飞区的规避，但仍需倾侧角翻转。王劲博[27]提出了基于凸优化和伪谱离散的垂直着陆运载器轨迹在线优化方法，但其通用性差，仅适用于简单模型。Sagliano等[28]采用自适应高维伪谱插值(Adaptive Multivariate Pseudospectral Interpolation, AMPI)算法实现了再入轨迹在线生成，但仅考虑了状态量偏差。

与一般再入轨迹设计方法不同，本文充分结合一子级返场轨迹面临的问题和需求，采用先给定侧向剖面再求解轨迹的设计策略：在侧向剖面设计了简单新颖、具备通用性的倾侧角剖面，在纵向剖面划分了物理意义清晰、贴合任务的不同飞行阶段，并采用分段优化方法设计了返场轨迹。在上述策略基础上，本文还进行了轨迹在线生成研究。首先根据任务特点，扩展了AMPI算法插值依赖的参数范围，在考虑分离扰动造成的偏差条件下，采用本文给出的轨迹设计策略计算离线轨迹数据库，进而根据实际飞行状态在线生成返场轨迹。

本文给出的轨迹设计策略思路独特，具备一定创新性和通用性，其中设计的倾侧角剖面形式简单，定义的纵向、侧向剖面飞行阶段划分目的明确，既适应了一子级大幅转向需求，又保证了倾侧角不翻转和轨迹光滑平稳。本文还对AMPI算法进行了扩展，使生成的轨迹更符合实际物理过程，保证了攻角连续变化，利于工程实现。

1 数学模型

本文的动力学模型采用不考虑地球自转的圆球模型，即

(1)

式中：r为飞行器地心距；θ和φ分别为经度和纬度；V为飞行器速度；γ为航迹角，是速度矢量与当地水平面之间的夹角；ψ为航向角，从当地正北方向顺时针测量；m为质量;σ为倾侧角；D、L分别为气动阻力与升力;g为重力加速度。

飞行器气动模型均表示为马赫数、攻角的函数。大气密度模型采用近似的拟合公式为

ρ=ρ0e(-h/hs)

(2)

式中：ρ0为海平面大气密度；hs为高度系数；h为飞行高度，上述变量均采用国际单位制。

2 轨迹优化设计策略

传统再入轨迹设计策略将纵向剖面和侧向剖面独立进行设计。首先设计纵向剖面，即将攻角或阻力加速度表示为速度的函数，得到攻角-速度剖面或阻力加速度-速度剖面。然后再根据飞行状态，计算满足拟平衡滑翔等条件要求的倾侧角大小并确定倾侧角方向，从而得到侧向的倾侧角指令。确定纵向和侧向指令后，即可得到飞行轨迹。

本文同样将侧向剖面和纵向剖面独立设计。与传统方法不同的是，本文先给定侧向的倾侧角-航向角偏差剖面，再采用分段优化策略求解攻角指令。上述策略的优点是：一方面，倾侧角变化过程连续平稳并且不会发生翻转，减轻了控制系统滚转通道压力；另一方面，在速度方向与飞行器-着陆场视线方向存在较大航向角偏差条件下，上述策略能够调整飞行方向对准着陆机场，满足一子级返场大幅转向需求。

2.1 倾侧角剖面设计

本文将倾侧角表示为航向角偏差的分段函数，并分别将两阶段命名为航向转弯段和航向微调段，如图1 所示。其中点A表示一子级返场轨迹初始状态，点B表示航向转弯段切换为航向微调段，点C航向角偏差为0°表示飞行航向已经对准目标机场。在航向转弯段，倾侧角保持较大幅值，且幅值随航向角偏差减小而逐渐减小(沿图1线段AB变化)。在这一阶段，大幅值的倾侧角使升力的侧向分量较大，能够提供较大的侧向机动能力，从而迅速调整一子级飞行航向。在航向微调段，倾侧角幅值较小并随航向角偏差减小而迅速收敛到0°附近(沿图1线段BC变化)。在这一阶段，一子级飞行航向基本对准着陆机场，不再需要进行大范围的航向调整，倾侧角只需在较小幅值内进行微调即可。

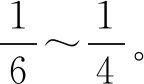
图1 倾侧角剖面Fig.1 Bank angle profile

根据设计的倾侧角剖面可知，在航向角偏差减小过程中，倾侧角随之减小；当飞行航向对准目标机场时，倾侧角恰好为0°。此时升力不再提供侧向机动能力，航向角偏差保持为0°，从而保证了倾侧角无需翻转。

倾侧角剖面表示为

(3)

式中：σA、σB、σC分别为倾侧角节点；ΔψA、ΔψB、ΔψC为对应的航向角偏差节点。

侧向剖面设计完毕后，通过数值优化方法，计算满足多种约束条件下的攻角指令。

2.2 优化模型

(4)

式中:α为攻角。

式(1)描述了飞行器三自由度运动学模型，其中轨迹控制量为攻角和倾侧角。本节为了更好地限制攻角变化过程，选择攻角变化率为控制变量。对应的，优化模型中的状态方程包括描述飞行轨迹的6个状态量和攻角，如式(4)所示。

为保证飞行轨迹变化平稳，选择航迹角变化率绝对值积分最小作为性能指标：

(5)

在本节建立的优化模型中，控制量为攻角变化率，其约束条件将在2.3节给出，在此仅给出攻角约束。需要强调的是，本文给出的优化策略将攻角作为状态量而非控制量。

αmin<α<αmax

(6)

式中：αmin、αmax分别为攻角的最小值和最大值约束。

过程约束方面，主要考虑法向过载、动压、热流密度等约束条件：

(7)

优化模型还要考虑终端经纬度、高度、速度等终端约束条件：

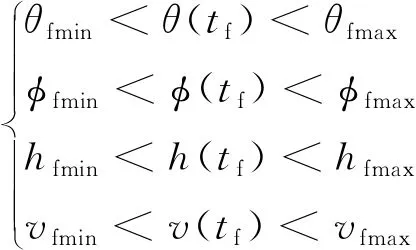
(8)

式中：θfmax、φfmax、hfmax、vfmax分别为期望的终端经度、终端纬度、终端高度、终端速度的最大值；θfmin、φfmin、hfmin、vfmin为对应的最小值。

2.3 分段优化策略

TSTO运载器分离后，一子级面临气动力过剩问题，且气动特性在不同速域内变化显著。上述特点导致分离后一子级的飞行轨迹容易产生反复跳跃，这对于大尺寸、大惯量飞行器的制导控制系统是极为不利的。

针对上述问题，考虑到分离时刻增高难以避免，同时希望返场轨迹保持平稳，本文将一子级返场轨迹的纵向剖面分为增高减速段和下降滑翔段。这两阶段的任务和特点存在显著区别，因而约束条件也不尽相同，无法通过统一的过程约束进行限制。在增高减速段，飞行器增高降速，动压减小，在此阶段要求航迹角始终大于零。在下降滑翔段，飞行器高度速度同时下降，在此阶段要求航迹角始终小于或等于零。经过上述两个阶段，飞行器逐渐以适当的能量状态飞行至着陆场附近，并调整飞行航向对准着陆场。对应的航迹角约束为

(9)

式中：γ1、γ2分别代表增高减速段和下降滑翔段的航迹角；γ1min、γ1max分别代表增高减速段航迹角最小值、最大值约束；γ2min、γ2max分别代表下降滑翔段航迹角最小值、最大值约束。

为避免飞行轨迹变化过于剧烈，还需要对飞行过程中的航迹角变化率进行限制。由于增高减速段气动力过剩，因而航迹角变化率幅值约束大于下降滑翔段。在返场飞行过程中，动压总的趋势是先减小后增大，因此增高减速段允许攻角变化率幅值大于下降滑翔段。

(10)

除上述约束外，还需以两阶段过渡时刻状态量和攻角连续作为约束条件，从而保证轨迹变化符合实际的物理过程，如式(11)所示。需要说明的是，由于倾侧角由倾侧角-航向角偏差剖面决定，当状态量连续时便可保证倾侧角连续，因此无需进行额外约束。

(11)

式中：t1f、t2i、x1f、x2i、u1f、u2i分别代表增高减速段结束时刻和下降滑翔段初始时刻的时间、状态量和控制量。

通过上述优化策略，本节将一子级返场轨迹优化问题转化为相应的最优控制问题，然后通过分段高斯伪谱法进行求解。有关高斯伪谱法原理介绍可见文献[29]。

需要补充的是，本策略存在一定局限性。传统方法在设计纵向剖面时可直观地对动压、过载和热流等约束条件进行限制，并且在给定纵向剖面后可快速确定倾侧角大小和方向。而本文需要通过数值优化方法求解纵向剖面并使其满足各项约束条件，相对而言计算量较大、计算时间较长。不过，后文给出的轨迹在线生成算法，使得上述策略同样具备在线应用潜力。

3 轨迹在线生成算法

本节针对TSTO运载器分离时刻扰动特点和攻角连续变化约束，扩展了AMPI算法进行高维插值依赖的参数范围。AMPI算法数据存储量小，计算速度快，可满足在线计算需求，具有广阔的应用前景。

AMPI算法的基本过程可划分为离线计算和在线计算两部分。离线部分根据定义的参数空间，在地面计算飞行轨迹数据库。在线部分根据初始状态相对标称状态的偏差，先插值得到低密度节点表示的飞行轨迹，再通过预先装订的变换关系将其转换为高密度飞行轨迹。通过将轨迹数据库装订在弹载计算机上，AMPI算法缓解了飞行过程中弹载计算机的计算压力。在线计算部分仅需根据初始时刻的实际状态，结合装订的轨迹数据库，即可快速地在线生成飞行轨迹。本方法存储量小、在线计算效率高。

3.1 AMPI算法流程

AMPI算法离线部分包括参数空间定义和离散化、飞行轨迹数据库计算和转换矩阵计算。首先，根据选定的描述初始偏差的参数定义参数空间并对其进行离散化。其次，通过第2节给出的分段优化策略计算飞行轨迹数据库。最后，离线计算出用于快速将低密度轨迹转换为高密度轨迹的转换矩阵。与文献[28]仅以轨迹状态量构建参数空间不同，本文将控制量纳入了参数空间，相应的算法流程如图2 所示。

在线部分包括相关子空间选择、低密度高维插值和LD-HD(Low Density-High Density)转换。首先，弹载计算机根据在线检测到的飞行状态确定相关子空间。其次，根据飞行状态和确定的相关子空间，通过张量积样条插值得到低密度节点表示的轨迹。最后，根据LD-HD矩阵(即后文将介绍的矩阵PFRP)在线生成高密度轨迹。

图2 AMPI算法流程Fig.2 Scheme of AMPI algorithm

需要强调的是，为减少存储量，离线得到的飞行轨迹数据库并非逐点存储在弹载计算机上，而是在每条飞行轨迹中，选择与较少数量FRP(Flipped Radau Pseudospectral)配点(简称低密度节点)对应的轨迹数据进行存储。此外，由于在线计算过程无需进行动力学积分运算，因此求解效率高、速度快，可满足在线计算需求。

3.2 参数空间定义及轨迹数据库生成

本文根据一子级返场轨迹特点，扩展了AMPI算法插值依赖的参数范围，将作为控制量的攻角纳入参数空间，使算法适用于一子级返场轨迹生成。

为了进行插值计算，首先需要对参数空间进行定义和离散化，然后计算飞行轨迹在各个插值节点的值。

(12)

在此基础上，取有限个离散点对每个维度的参数进行离散化：

(13)

从而得到由n1×n2×…×nd个节点表示的d维网格：

(14)

TSTO运载器分离时存在明显的分离扰动，考虑到一、二级均为面对称飞行器，本文假设扰动主要作用在纵向平面内，即扰动影响的轨迹状态量主要是纵向平面内的速度和航迹角。同时，分离扰动还会对控制量攻角产生显著影响，使其偏离标称值。文献[28]仅考虑了状态量初始偏差，而将初始控制量作为生成的轨迹结果，这对于空间再入飞行器是可行的。但对TSTO运载器一子级而言，攻角变化相对缓慢，特别是考虑到高动压的飞行状态，攻角难以瞬间调整到期望值。因此，一子级返场轨迹在线生成需要将考虑偏差的攻角作为初始条件，即在状态量基础上扩展插值依赖的参数范围，将控制量攻角纳入定义的参数空间。

根据上述分析，考虑纵向平面状态量速度、航迹角和控制量攻角这3个参数，定义3维参数空间，各维度取3个节点。对应的初始状态如下：

(15)

式中：X*(t0)为标称轨迹初始状态对应的参数。

至此完成了参数空间定义和离散化过程，然后以参数空间内各个网格点作为轨迹设计的初始状态，通过2.3节给出的分段优化设计策略离线计算一子级返场轨迹数据库。

3.3 在线低密度插值

本节给出如何根据实时飞行状态和离线轨迹数据库，快速计算以低密度节点表示的飞行轨迹。其基本思路为，根据离线轨迹数据库中给定的低密度节点值，通过张量积样条插值方法计算给定插值点的状态量、控制量等轨迹参数。

首先，需要在离散化的参数空间中确定与当前状态对应的相邻参数空间，在此将其命名为相关子空间。插值过程均在相关子空间中进行，且插值点与相关子空间节点越接近，插值结果越准确。以二维插值为例，相关子空间如图3 所示。图中，X1、X2分别表示二维插值需要的参数，x1、x2分别表示参数的实际值，角标L和U分别表示参数的下界和上界。

图3 相关子空间示意图Fig.3 Reference subspace diagram

确定各维度插值点的相关子空间后，通过张量积样条插值方法对初始偏差进行插值，得到某一时间节点的轨迹值。张量积样条插值方法可参考文献[28]。在时间节点的选择方面，本文采用FRP方法得到配点作为插值节点，相关分析可参照文献[27]。

经过上述过程，即可由离线轨迹数据库插值得到低密度轨迹。在此可认为该轨迹是对最优轨迹较好的近似，其求解过程既满足实时性需求又避免了过大的计算负担。

3.4 低密度-高密度转换

本节给出如何避免在线插值的巨大计算量和存储全程轨迹的庞大存储量的前提下，将低密度轨迹转化为具有高密度节点的飞行轨迹。

仍然采用FRP方法确定高密度节点，并通过计算飞行轨迹在这些节点的值替代计算全程飞行轨迹。由伪谱离散方法相关原理可知，当低/高密度节点数目确定后，相对应的转换矩阵也是确定的，与飞行状态无关，可由离线计算得到。

设低密度插值中共取NLD+1个FRP插值点(NLD个FRP节点和-1)，通过对时间tLD、状态量XLD、控制量ULD进行插值，得到各个插值点处的对应值。XLD和ULD向量的矩阵维数分别为ns×(NLD+1)、nc×(NLD+1)，其中ns和nc分别表示求解问题的状态量和控制量数目。将XLD和ULD写成(ns+nc)×(NLD+1)维的矩阵TLD：

(16)

对应的，高密度插值矩阵THD为

(17)

式中：NHD+1为高密度插值的离散节点数。此外，插值节点对应的物理时刻可以离线计算好，无需在线计算。

于是，将低密度插值转换为高密度插值的问题即变为，如何求矩阵TLD和矩阵THD之间的转换关系。下面，考虑多项式插值公式

(18)

式中：Fi表示低密度插值量，可以由矩阵TLD的对应行替代。令时间变量τ∈[>-1,1]在NHD+1个高密度节点分别取值，可以得到

(19)

式(19)可以推广到矩阵THD的所有行，并表示为

THD=TLDPFRP

(20)

式中：矩阵PFRP为

(21)

此外，还需将插值用到的伪谱时间转化为实际的物理时间。具体公式为

(22)

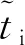
经过上述过程，飞行轨迹的在线生成简化为在少量节点的插值和矩阵乘法，大幅降低了计算负担和数据存储量。

4 数值仿真

本节首先对返场轨迹优化设计策略进行仿真验证，并以此为基础构建离线轨迹数据库，进而验证基于AMPI的返场轨迹在线生成策略。本文仿真采用的编程环境为MATLAB R2016b，CPU为Intel Core i5-8250U，主频3.4 GHz。

4.1 返场轨迹分段优化

采用本文提出的设计策略得到的飞行轨迹如图4 所示。可以看出，高度曲线十分明显的分为增高减速段和下降滑翔段，且在两阶段均光滑、平稳、无跳跃，实现了预期效果。由经纬度曲线可以看出，飞行器从分离点缓慢转弯直到对准着陆机场，并到达着陆机场附近。

通过图5 所示的航向角偏差曲线和倾侧角曲线可以看出：在航向转弯段，倾侧角保持较大幅值，升力提供较大的侧向机动能力使飞行器迅速转弯，航向角偏差随之快速减小；在航向微调段，航向角偏差已经接近于零，飞行器基本对准着陆机场，此时倾侧角在小幅值内缓慢变化且未发生翻转，航向角偏差逐渐收敛到零，这表明一子级飞行航向完全对准着陆机场。在整个过程中，倾侧角始终朝向一个方向逐渐减小到零。而若采用传统再入轨迹设计方法，侧向剖面的航向角误差走廊将导致倾侧角多次翻转，对一子级控制系统造成过大压力，甚至无法实现。

本文优化模型以攻角变化率代替攻角作为控制变量，其主要目的是防止攻角过快变化，本质上关注的仍是攻角变化过程本身。由图6 可以看>出，返场过程中攻角曲线连续平稳，幅值始终在约束范围内。在增高减速段，飞行器动压不断减小，为满足这一阶段航迹角大于零的约束条件，攻角持续增大。在下降滑翔段，前期气动力过剩，攻角不断减小；后期随着飞行速度降低，攻角再次增大以保证终端高度。在整个飞行过程中，两阶段的攻角变化率均符合约束条件，有利于控制系统实现。

表1 一子级标称条件Table 1 Nominal conditions for first stage

图4 一子级优化轨迹Fig.4 First stage optimization trajectory

图5 侧向剖面随时间变化曲线Fig.5 Time history of lateral profile

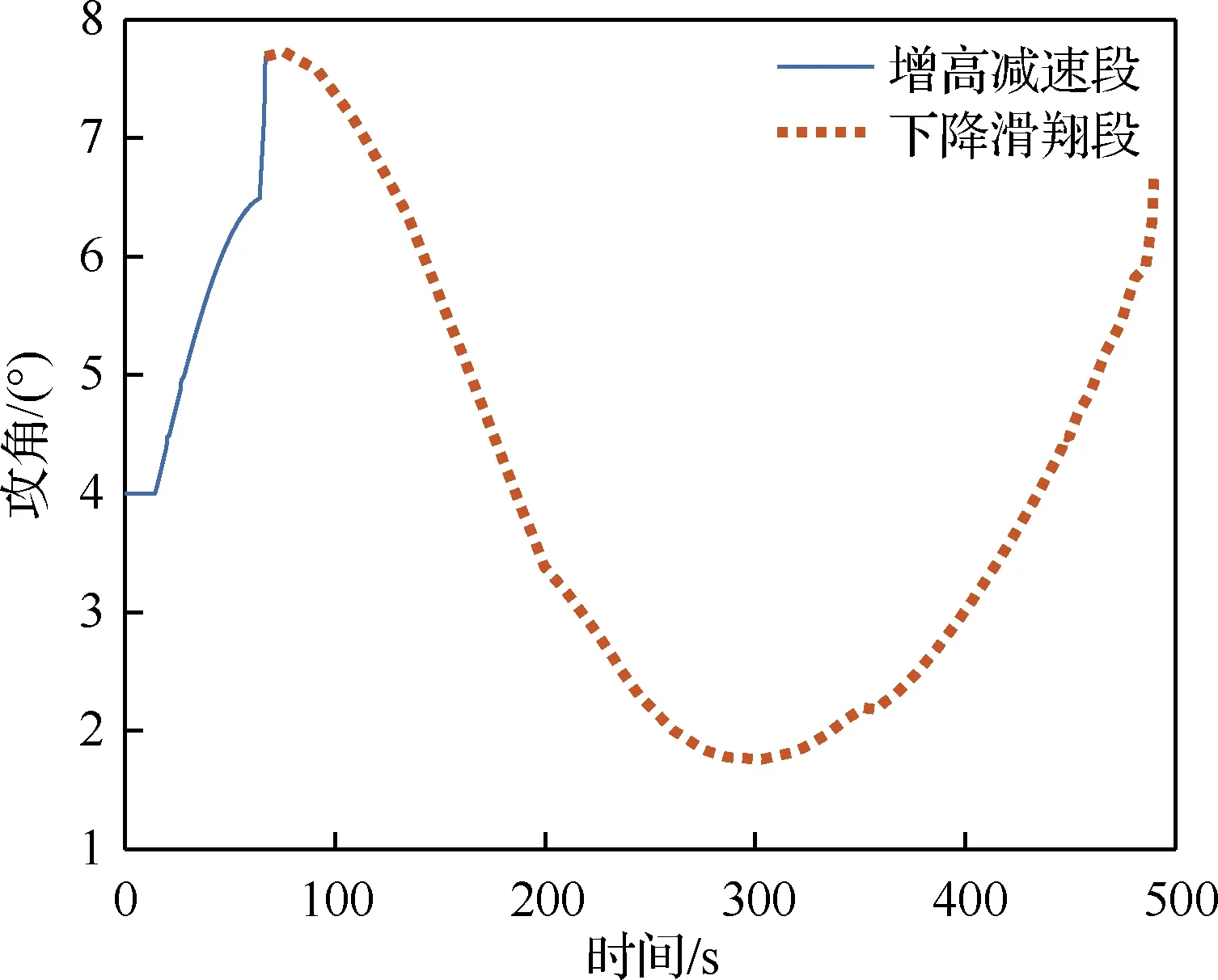
图6 攻角随时间变化曲线Fig.6 Time history of angle of attack

相比之下，现有文献给出的再入轨迹设计算法难以满足本文提出的一子级返场轨迹设计需求，此处不再进行对比。

4.2 返场轨迹在线生成

4.1节的轨迹设计未考虑分离点状态偏差。在实际飞行过程中，一二级分离过程存在很大的分离扰动，这将对飞行状态产生显著影响。假设组合体上升段轨迹跟踪理想，考虑到分离过程非常短暂，认为分离扰动仅对纵向飞行剖面的状态量速度和航迹角以及控制量攻角产生比较明显的干扰。

分离后一子级初始偏差节点如下所示：

(23)

考虑上述初始状态量和控制量偏差，通过前面介绍的分段优化算法设计出离线轨迹库。相关结果如图7 所示。若需要考虑更大偏差，只需要适当降低节点密度或增加与更大偏差对应的参数网格数量即可。前者会导致精度有所降低，但在合理范围内可接受；后者会增加离线计算量和在线存储量，但不会降低精度。

通过图7 可以看出，在构造的离线轨迹数据库中，轨迹各状态量符合给定的各项约束条件。同时，在各组条件下倾侧角均未发生翻转，符合2.1节分析。

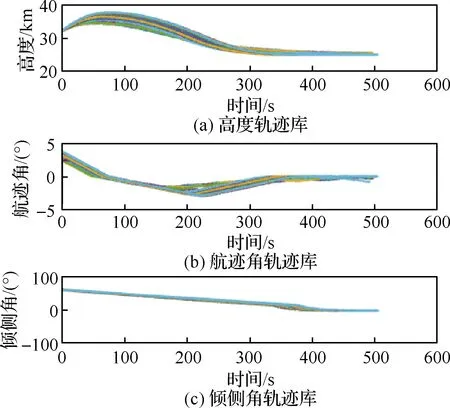
图7 离线轨迹库Fig.7 Offline trajectory database

在上述离线轨迹库基础上，根据分离时刻的实际飞行状态，采用AMPI算法进行在线轨迹生成。由AMPI算法原理可知，一般而言初始偏差取值与参数网格节点距离越远则精度越低。因此，可将各参数网格节点中点对应的条件看作极限偏差条件。以如下极限初始偏差为例：

(24)

图8将AMPI算法在线生成的飞行轨迹和采用AMPI算法给出的控制量进行积分得到的轨迹进行了对比。可以看出，AMPI算法成功生成了符合要求的飞行轨迹，且该轨迹与积分得到的轨迹几乎完全重合，说明AMPI算法具备足够高的在线计算精度。

为进一步验证AMPI算法的计算精度，在多组不同初始偏差条件下，采用AMPI算法进行在线轨迹生成。初始状态偏差如表2 所示，最终得到的轨迹终端误差如表3 所示。从表3 可知，终端高度偏差普遍小于100 m且最大值约120 m，终端速度偏差小于6 m/s，终端航迹角可以忽略，终端航向角偏差普遍小于0.2°。上述仿真结果说明，AMPI算法生成的轨迹能够准确地表示出一子级返场过程，且终端误差较小，能够满足轨迹在线计算的精度要求。

最后，对AMPI算法计算效率进行了分析，并与本文给出的优化策略进行了对比。在离线轨迹数据库生成过程中，不同初始条件的轨迹优化耗时大约30～60 s，而对应的AMPI算法生成轨迹仅需0.2 s以内。从图9 可见，AMPI在线生成的轨迹和离线优化得到的轨迹基本重合。这说明AMPI算法具备在线轨迹生成潜力，并且生成的轨迹十分接近最优轨迹。

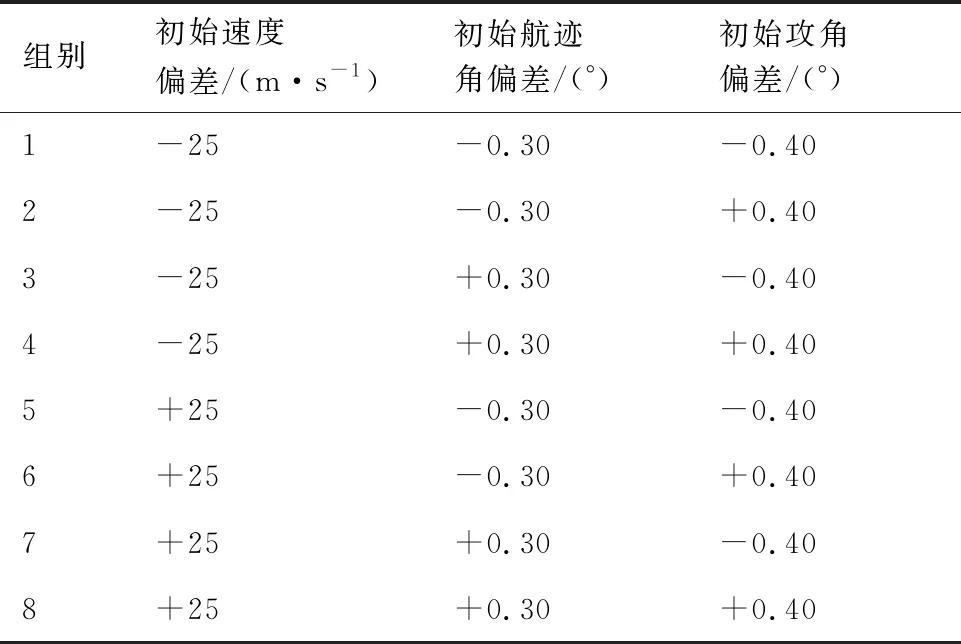
表2 初始偏差取值Table 2 Values of initial errors

表3 AMPI轨迹终端偏差Table 3 Final errors of AMPI trajectory

图9 AMPI轨迹和优化轨迹Fig.9 AMPI trajectory vs optimization trajectory

5 结 论

1) 提出的侧向剖面的倾侧角-航向角偏差策略能够满足两级入轨运载器一子级返场需求。在航向角偏差快速调整并逐渐减小至零的同时，轨迹的倾侧角变化连续平缓且未发生翻转，更符合一子级返场需求。

2) 提出的纵向剖面的分段优化策略合理可行，适用于一子级返场轨迹优化。生成的轨迹各段状态量变化平稳，高度曲线全程无跳跃，能够满足各项过程约束和终端约束。

3) 扩展了AMPI算法的参数空间，并成功应用于一子级返场轨迹在线生成问题。扩展后的AMPI算法保证了攻角连续变化。计算精度方面，终端高度偏差普遍小于100 m，速度偏差小于6 m/s，航迹角和航向角偏差可忽略，满足在线轨迹生成需求。计算效率方面，耗时在0.2 s以内，具备在线应用潜力。