空气轴承支撑的燃料电池离心空压机转子动力学分析
靳彩妍,徐方程,吴孟龙,范俊岩,辛军
(1.奕森科技(上海)有限公司,上海 201703;2. 大连理工大学控制科学与工程学院,辽宁大连 116024;3.大连理工大学工业装备智能控制与优化教育部重点实验室,辽宁大连 116024)
0 引言
燃料电池是一种能直接把化学能转换为电能的装置。燃料电池内部反应过程的本质是氧化还原反应,燃料通过阳极侧进入,空气或氧气通过阴极侧进入,二者在电解质两侧分别发生燃料氧化反应与还原反应,电子流经外电路做功,从而产生电能[1]。因为燃料电池的这种能量转换方式不用经过热机过程,不被卡诺循环约束,所以能量转换效率很高。
燃料电池按照电解质可以分为:质子交换膜燃料电池(PEMFC)、磷酸型燃料电池(PAFC)、熔融碳酸盐燃料电池(MCFC)、直接甲醇燃料电池(DMFC)及固体氧化物燃料电池(SOFC)等[2]。
燃料电池用空压机需要满足无油性、高效率、小型化和低成本、低噪声、动态响应快等特点。目前,常用的燃料电池空压机主要有离心式、罗茨式、螺杆式3种,离心空压机是通过旋转叶轮对气体做功[3],在叶轮与扩压器流道内,利用离心升压和降速、扩压的作用,将机械功转化为气体内能,具有机构紧凑、响应快、寿命长和效率高的特点。
空气轴承是一种自润滑动压滑动轴承,相比于传统的油润滑滑动轴承和滚动轴承,空气轴承具有高转速、零环境污染、工作温度高及寿命长特点使其与燃料电池系统无油环境要求匹配。
波箔型径向空气轴承是空气箔片轴承的一种结构形式,如图1所示。其由底层的波纹箔片和顶层的平箔片共同组成。建立箔片结构刚度模型是研究箔片轴承物理特性的重要一环,也是进行转子动力学分析的重要参数。
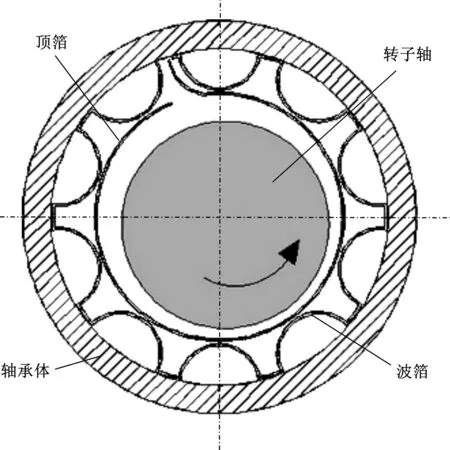
图1 箔片空气轴承结构
1 转子动力学计算
由于燃料电池空压机转子高转速、空气轴承低阻尼特性[4],设计转子要求是刚性转子,即空压机额定运行转速要求远低于转子的一阶弯曲临界转速。
1.1 空压机结构设计
两级压缩空压机结构如图2所示,主要由低压级叶轮、高压级叶轮、主轴、空气轴承、永磁同步电机、电机冷却水套及壳体等部分组成。

图2 两级压缩燃料电池空压机结构
离心式空压机的工作转速越高,其压比越高,但高转速下转子的稳定性需要重点关注,综合考虑各方因素下,整个空压机转子设计为:电机位于转子中间,两个径向空气轴承分别位于电机两侧,两个止推空气轴承位于低压极端,两个叶轮分别位于转轴的两端,使得转子的重心尽量靠近中心,提高转子稳定性。
1.2 空气轴承刚度阻尼计算
空气轴承不仅提供支撑作用,更是空压机转子轴承系统的重要部分,波箔型空气轴承的动力特性对整个转子系统有很大的影响。根据参考文献[5],基于单个波纹箔片非线性刚度模型,通过有限差分法耦合求解气体Reynolds方程、气膜厚度方程,从而求解出设计转子载荷下的气弹耦合径向空气轴承刚度阻尼值。
求解空气轴承刚度阻尼系数的假设如下:
(1)在空气膜厚度方向上,空气压力认为是恒定的。
(2)空气在轴承顶箔表面上的速度为0,在转轴表面上的速度为Rω。
(3)气体为理想气体。
(4)气体是绝热的。
通过以上假设,Reynolds方程可写为
(1)
式中:r为轴承圆周方向坐标;
z为轴承轴向长度坐标;
R为轴径半径;
h为气膜厚度;
p为气膜压力;
μ为气体动力黏度;
Ω为轴径转速。
而箔片空气轴承气膜厚度方程为
h=h0+ecos(θ-φ)+ε
(2)
式中:h0为箔片空气轴承的名义半径间隙;
e为轴径的偏心距;
θ为轴承圆周方向角度;
φ为偏位角;
ε为平箔片表面计算节点在轴承径向方向的变形量。
求解得到设计载荷下的径向轴承刚度阻尼系数随转速变化曲线,重力方向为x如图3和图4所示。
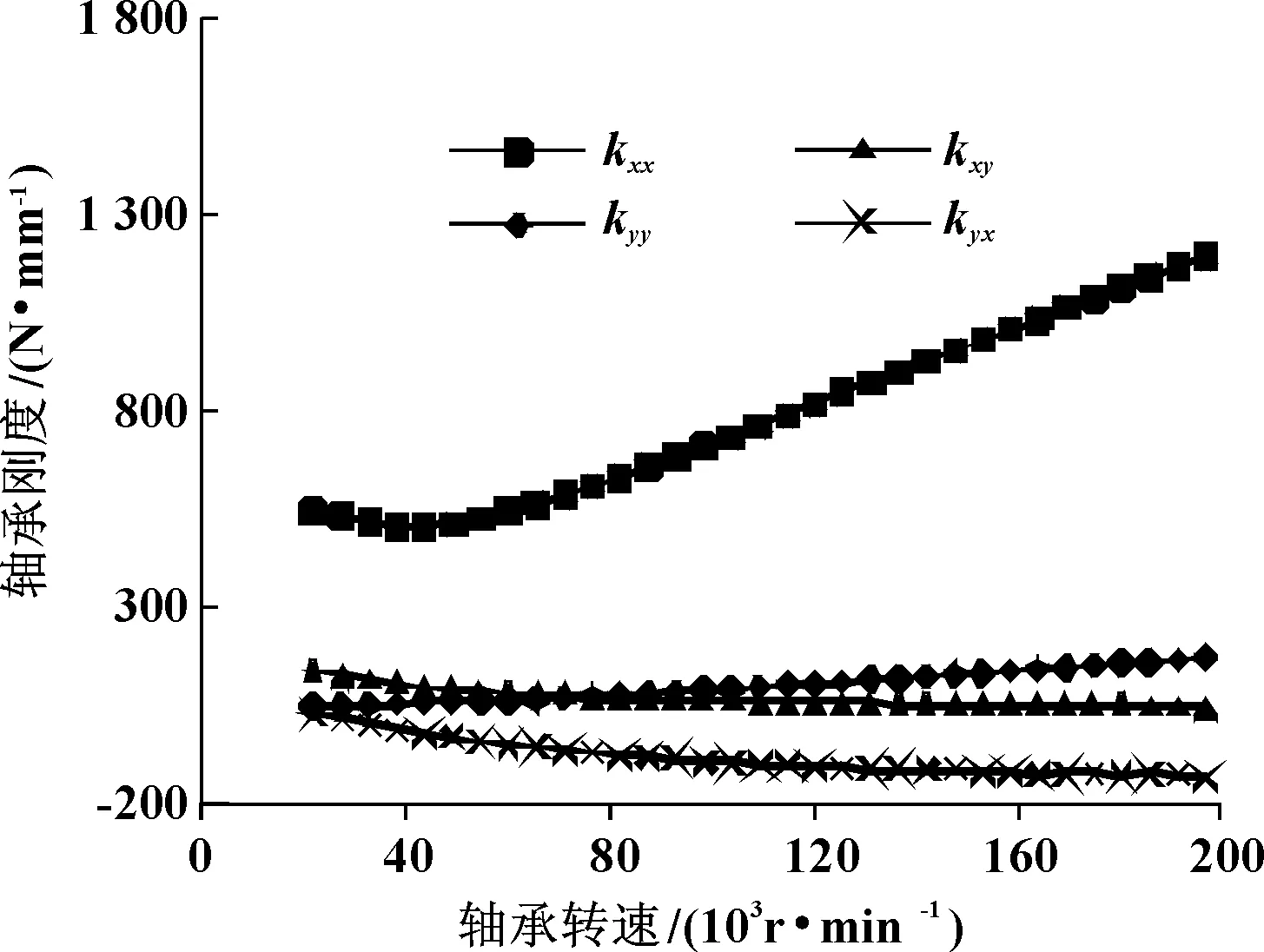
图3 径向空气轴承刚度系数随转速变化曲线
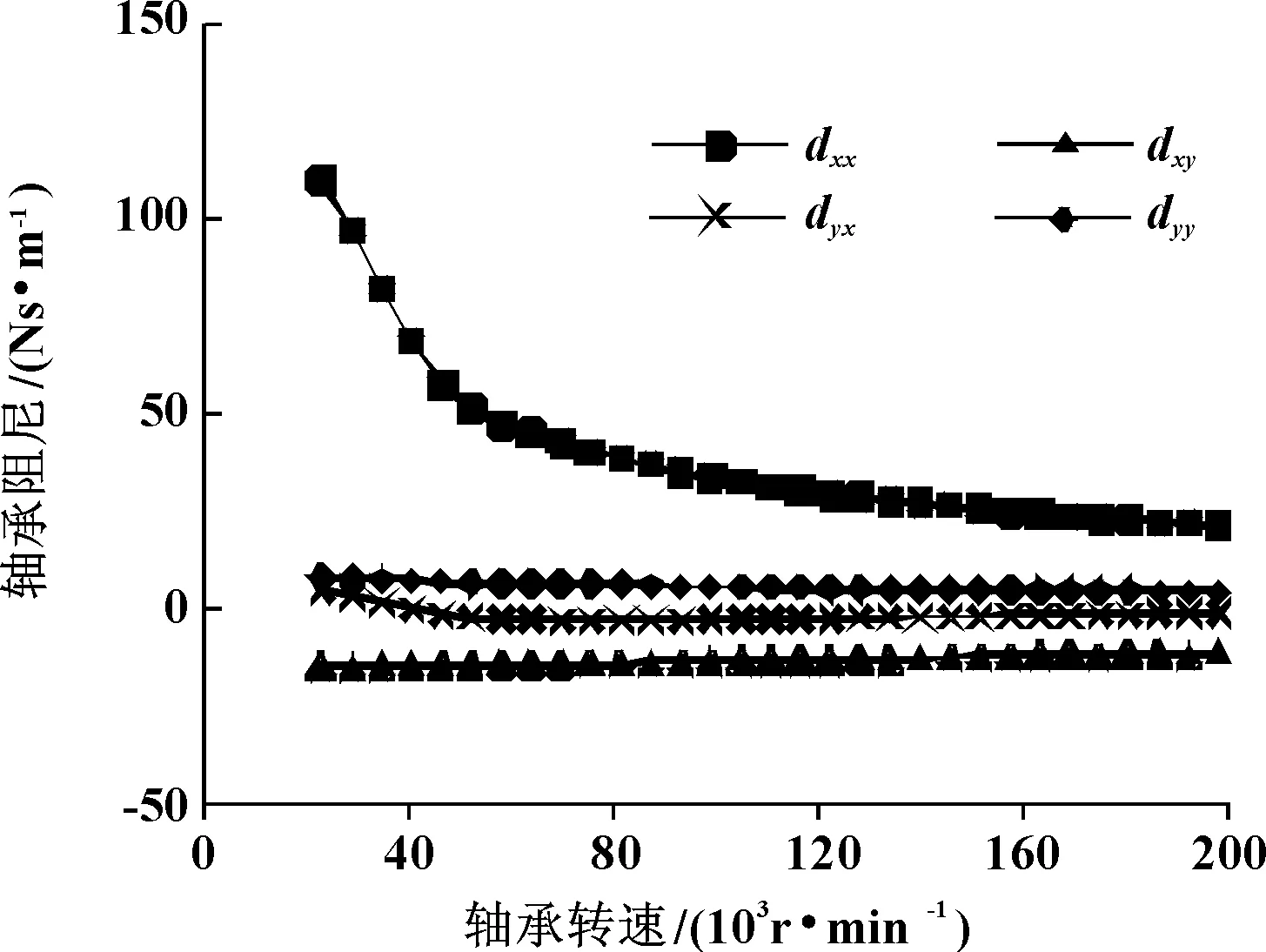
图4 径向空气轴承阻尼系数随转速变化曲线
1.3 空压机转子临界转速
1.3.1 转子建模
利用DyRoBes软件DyRoBes-Rotor转子动力学软件包,对燃料电池离心空压机转子进行有限元建模,模型如图5所示。
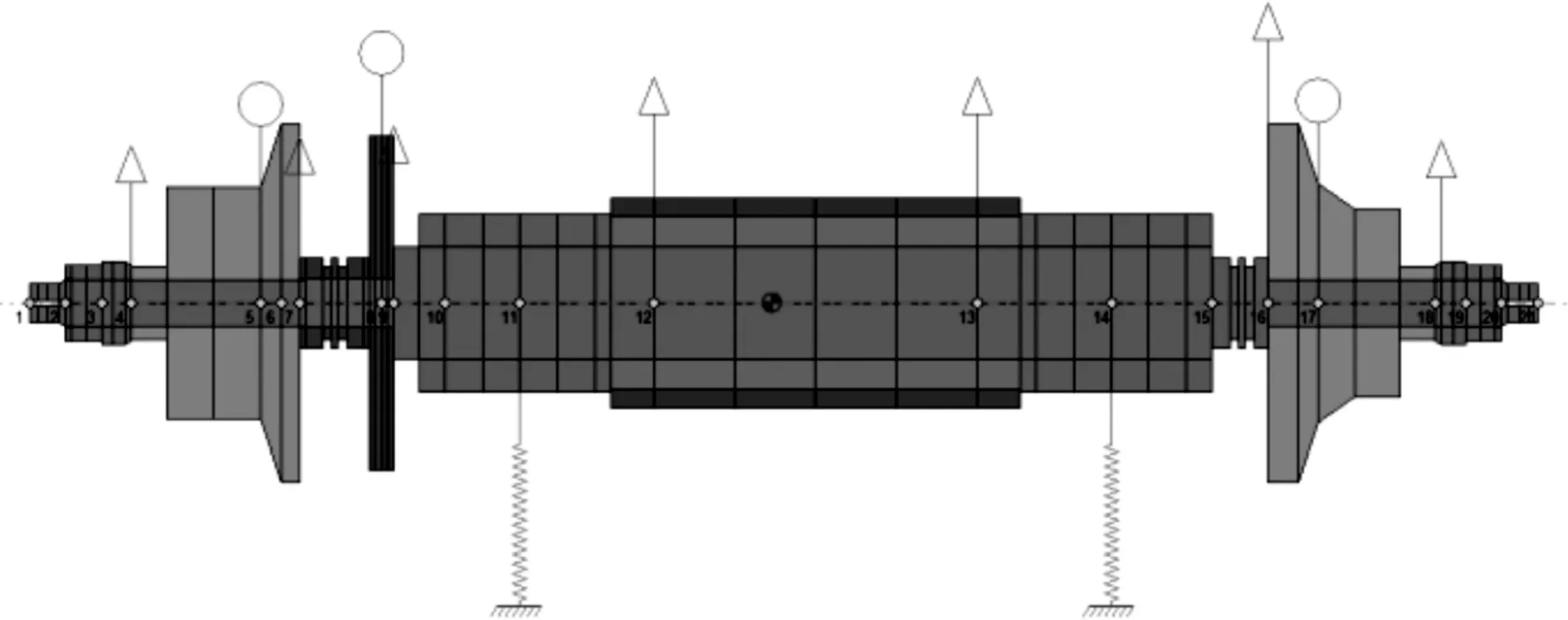
图5 两级压缩燃料电池空压机转子模型
1.3.2 转子临界转速计算
由于空气轴承阻尼较小,转子系统临界转速可以只计算无阻尼状态下的,系统临界转速计算控制方程为:
(3)
式中:kxz为转子系统的刚度系数矩阵;
Mxz为转子系统的质量矩阵;
ωi为转子系统临界转速;
yi为转子系统临界转速对应的振动向量。
计算得到空压机转子临界转速见表1。

表1 空压机临界转速结果 Hz
一阶临界转速对应模态振型如图6所示为圆锥刚体模态,二阶临界转速对应模态振型如图7所示,三阶临界转速对应模态振型如图8所示,为一阶弯曲模态。当运行转速达到临界转速附近,转子将会处于共振状态,如果系统阻尼较小,会造成转子振动应力过大而出现断轴、轴承损坏等失效。

图6 一阶临界转速111 Hz,圆锥刚体模态

图7 二阶临界转速129 Hz,圆锥刚体模态
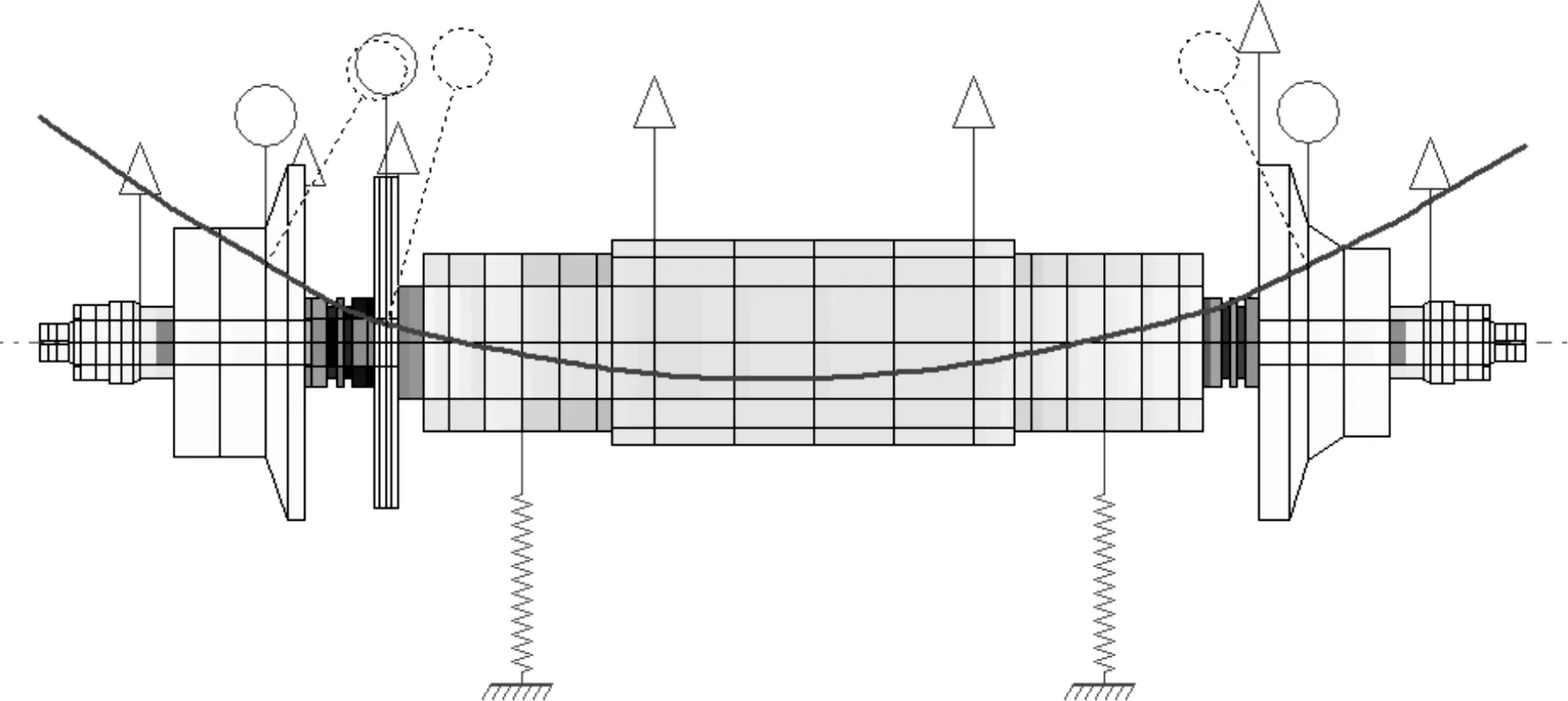
图8 三阶临界转速3 168 Hz,弯曲模态
燃料电池空压机转子设计额定转速是2 000 Hz,通过计算现有转子的一弯临界转速是3 168 Hz,运行额定转速是一弯临界转速的63%,根据API[6]对刚性转子定义,转子额定转速低于70%一弯临界转速的转子可视作刚性转子,满足设计初始目标。
2 空压机转子稳定性分析
根据气弹耦合方法计算不同转速下的轴承刚度阻尼系数,导入转子动力学计算文件,计算不同转速及转子不平衡量下每个节点的跳动位移值,为方便与后续试验测试结果对照,选取低压端压轮锁紧螺母端部节点,即模型图5中的节点1处位移值作为稳定性评估参考点。转子不平衡量加载按照G6.3精度[7]加载在转子的设定平面上,如图5中箭头所示。计算结果如图9—图11所示。
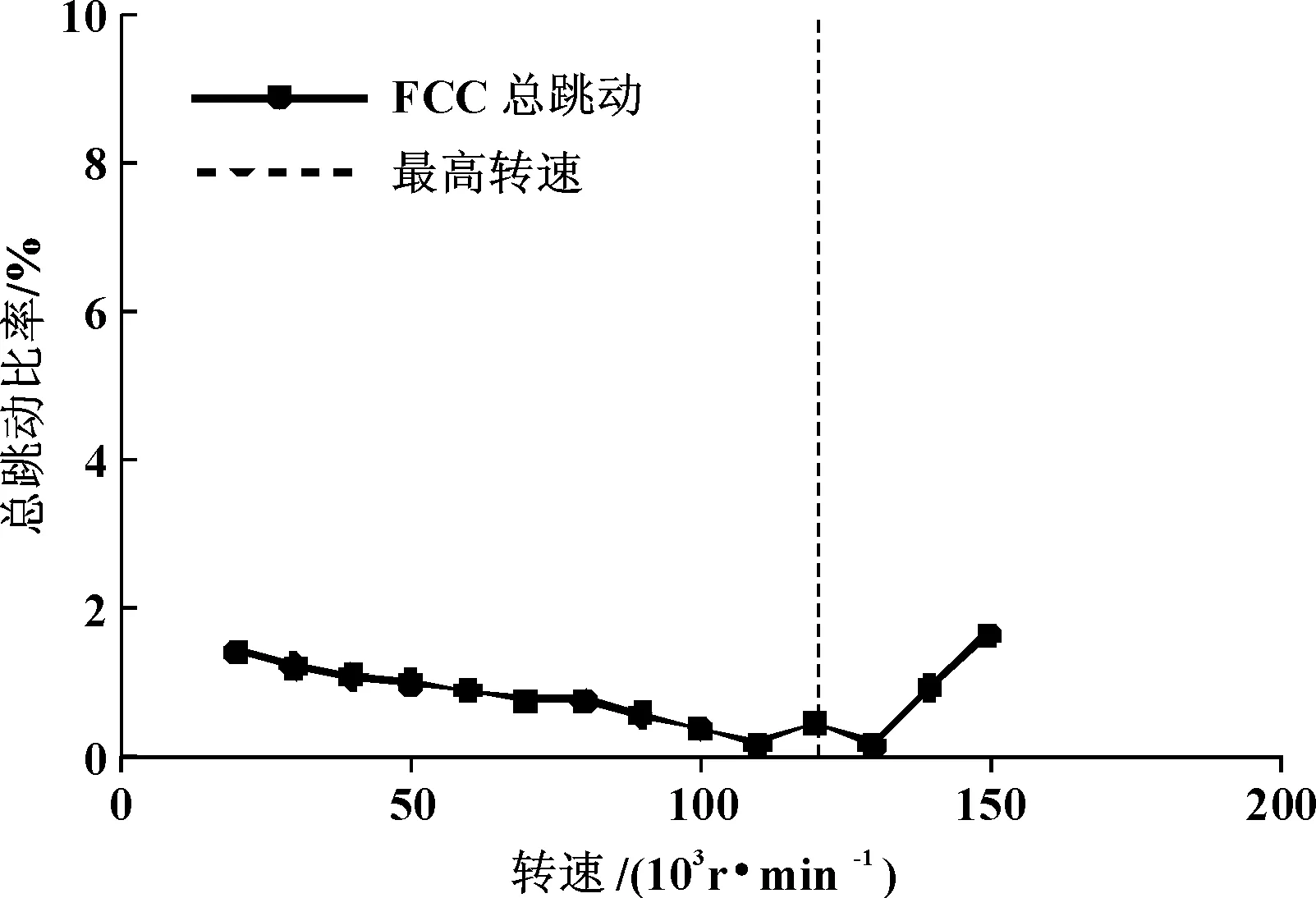
图9 燃料电池空压机测点1轴心位移值
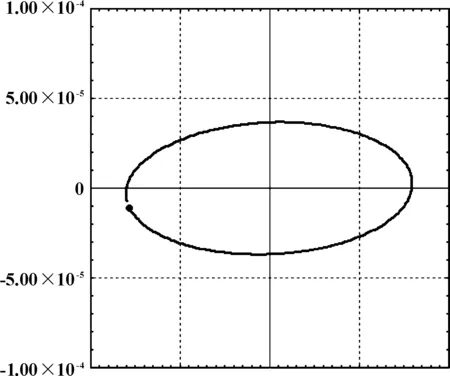
图10 转子轴心轨迹

图11 燃料电池空压机轴承受力
通过转子动力学稳定性计算,在工作转速1.20×105r/min范围内,轴心位移跳动比率都是低于5%,远低于设计允许跳动比率20%[8],则转子在额定转速范围内可稳定运行;另外选取转速1.20×105r/min下,测点位置的轴心轨迹如图10所示为椭圆状。计算得到径向空气轴承在每个转速下的受力情况如图11所示,由于转子重心位置偏向低压端轴承,低压端空气轴承在额定转速范围内受力大于高压端轴承受力,转速1.20×105r/min下轴承最大载荷为60 N,低于轴承设计承载能力100 N,则轴承在整个转子运行状态下可靠性达到设计目标。
3 结束语
根据气弹耦合方法求解出空气轴承的刚度阻尼系数,带入设计转子系统中计算得到转子临界转速远高于转子额定运行转速,符合刚性转子的设计目标,并且其轴心轨迹跳动低于20%,符合转子稳定性要求。在转子额定转速范围内,轴承最大受力60 N远低于轴承设计承载能力100 N,轴承在整个运行状态下都是可靠的。
目前转子设计在额定转速下可以稳定运行,并且余量较大,进一步优化方向可以减小轴径及轴承,以提高整个转子系统的响应性。

