基于模糊关联规则的教育大数据挖掘研究*
吴修国 邢奥林

摘 要:利用数据挖掘技术发现高等院校教学管理数据库中蕴涵的有价值的规律和知识,可为高校教学与管理决策提供科学合理的数据支撑。传统的Apriori算法在关联规则挖掘中存在“尖锐边界”问题,严重影响挖掘结果的科学性和有效性;基于模糊集理论的关联规则挖掘尚存在计算时间复杂度较大、内存占用过多以及耗时较长等问题。文章基于传统模糊关联规则方法,并结合AprioriTid思想提出一种改进的模糊关联规则挖掘算法,通过不断更新事务数据库,提高扫描数据库的效率;并将其应用在高等学校教育数据挖掘中,对学生课程成绩进行分析,发现课程之间的联系。实验结果表明,该算法可有效降低数据挖掘时间并减少内存消耗,挖掘结果能够发现教学中的规律,从而有效指导教学与管理工作。
关键词:教育大数据;数据挖掘;模糊关联规则
中图分类号:G64 文献标志码:A 文章编号:1673-8454(2020)21-0067-05
一、引言
当前,很多高校都开发了教务管理系统,以实现对教学过程中各项事务的收集、查询和简单统计。然而,相关数据分析还处于比较低级的水平,迫切需要一种数据处理技术,来分析海量教育数据背后隐含的关联和规律,为管理决策提供数据支撑与依据。关联规则数据挖掘作为教育大数据分析的一种重要方法,可发现海量信息中的关联关系,从而获得隐藏的信息与知识,为科学决策提供依据,目前被广泛运用于商业、科技、安全等方面。传统的关联规则挖掘算法更适合对离散的数据进行处理,但是教育领域存在着大量的连续型数据,不适合用布尔值来表示。如果采用硬性的离散化划分策略,则会导致所谓的“尖锐边界”问题,严重影响结果的真实性。[1]为了解决这些问题,许多国内外研究者对其展开了研究,比如通过引入模糊集理论,得出模糊关联规则挖掘模型,在处理连续型数据划分问题上取得了不错的效果。[2][3]然而,数据模糊化处理增加了数据量,增加了内存占用率和时间空间的消耗。基于上述分析,本文在模糊关联规则算法的基础上,引入AprioriTid优化的思想,在扫描数据库的同时生成新的项目集事务数据库;并将其应用在高等学校教育数据挖掘中,对学生课程成绩进行分析,发现课程之间的联系。
二、相关文献研究
近年来,随着网络技术、信息技术以及数据挖掘技术的迅速发展,越来越多的数据挖掘领域的研究人员希望能提取出教育数据背后的知识和信息。其中,关联规则在教育大数据中的应用有着重要的意义。
文献[4]应用关联规则算法对远程考试题目的考查知识点进行了关联分析,对考试和教学开展起到了积极作用;文献[5]首先将学生成绩转换为布尔型表达,之后再利用关联规则挖掘,得出课程之间的联系;文献[1]将事务项目数据转化为项目事务数据库,剔除最小支持度不满足的项集,通过连接生成新的候选集只需要通过取交集计算支持度,省去了剪枝过程中反复比较的过程;文献[6]提出不断迭代新事务数据库,每一次计算支持度都从新产生的事务数据库搜索,通过不断产生新的频繁项目集,不断剪枝,使新事务数据库越来越小,从而达到提高效率的目的;文献[7]提出通过减少事务数据库中无用数据,根据有序排列减少对比次数来提高效率;并且提出了另一种离散化方法,采用数据宽度非固定的方法,根据具体情况进行调整,以此提高结果的准确性。
上述研究基本上都是基于Apriori算法进行的,由于其只能处理离散数据,所以必须将连续数据处理成离散区间,会导致“尖锐边界”问题,破坏数据内在的联系,势必影响到关联规则的科学性。为此,有研究者將模糊集理论引入到关联规则中,形成了“模糊关联规则”。文献[2]针对经典模糊关联规则挖掘算法中,隶属度函数的选择“硬化”问题和数据集本身存在的不确定性问题进行了改进,通过对不同项之间的隶属度函数、不确定度和非隶属度函数进行分析,生成关联规则;文献[8]针对目前关联规则算法处理高偏度数据存在的较多问题,应用抽样技术和聚类算法,提出了一种解决连续数据离散化问题的算法。通过聚类的方法对属性值进行分类,每一类构成一个区间,作为一个单独的属性;文献[9]应用模糊集软化数量型属性划分边界,通过采用模糊c-均值[10]算法划分模糊集,然后采用遗传算法训练分类系统,从而获得更好的精确度。然而,上述方法挖掘过程复杂,时间复杂度高,不利于运用在教育大数据上。
针对以上问题,本文在结合传统关联规则算法和模糊关联规则算法的基础上,将连续性数据模糊化处理,利用隶属度函数划分为模糊集合,再将模糊集中的元素当成普通单一元素处理,从而能够按照传统Apriori算法进行挖掘,并通过不断更新事务数据库,剪去事务数据库中没有意义的数据,达到提高扫描效率的目的。
三、改进模糊关联规则数据挖掘算法与性能分析
关联规则挖掘算法简单,适用性强,可操作性高,基本思想是对项目集合或者事务集合中的频繁项集,以及频繁项目集中符合要求的关联规则进行挖掘。众多关联规则挖掘算法中,最具代表性的算法是Apriori算法[11]以及FP-growth算法[12]。
在关联规则分析和构建过程中,包含如下定义和概念:
(1)项(Item)。关联规则数据中最小的单位,项的集合成为项集,其中含有k个项的项集成为k-项集。
(2)支持度(Support)。该项集在整个数据集中出现的频率,表示为:Support(X→Y)=P(X∪Y)=(|D(X) |)/(|D|),其中X和Y为项集,D为数据集。
(3)置信度(Confidence)表示包含X的事务中出现Y的条件概率,表示为:Confidence(X→Y)=P(X/Y)=(Support(X∪Y))/(Support(X))。
(4)如果项集X的支持度大于设定的最小支持度,那么就可以称该项集为频繁项目集。
(5)如果关联规则X→Y的支持度和置信度都大于设定的最小支持度和最小置信度,则称X→Y为强关联规则。
在传统的关联规则数据挖掘算法中,需要对连续型数据进行离散区间的划分。这种项目集划分往往是基于精确的数值进行截断,项目要么属于这个区间,要么属于其他区间,存在着严重弊端,例如,学生成绩60分以上是及格表示成绩优,60分以下为不及格表示成绩差。虽然59分和61分只相差两分,但却属于两个完全不同的区间。显然,这样的划分过于绝对,不利于表现出真实的区别,严重影响了结果的真实性。因此,可以引用模糊理论对数据进行模糊处理,通过对应模糊区域的隶属度函数,将连续的属性划分为多个模糊区域。例如,一个学生课程成绩数据库Ti={t1,t2,t3,…,tn},课程属性集Wj={w1,w2,w3,…,wn},由对应领域专家给出隶属度函数,将学生成绩这一连续型数据进行模糊化处理,划分为多个模糊集合。比如将成绩划分为{high,medium,low},课程属性集则划分为{w1high,w1medium,w1low,w2high,w2medium,w2low,…,wmhigh,wmmedium,wmlow}。
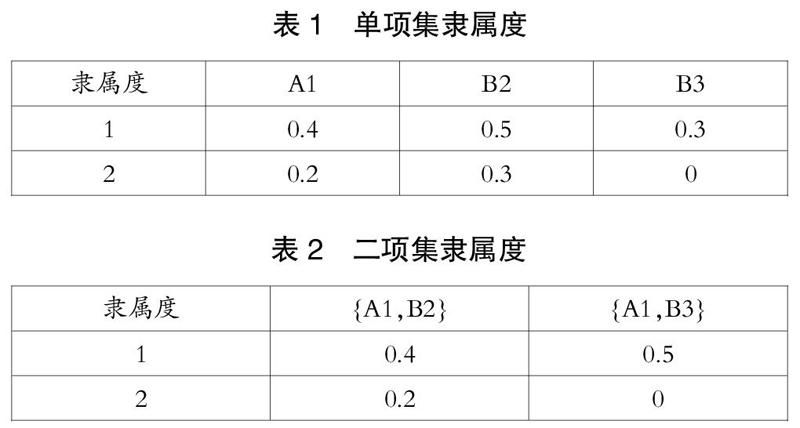
根据隶属度函数计算各个数据对模糊属性集的隶属度,所有的模糊属性隶属度取值都在区间[0,1]中。与传统Apriori算法不同,支持度不再是事务对项目集支持的数量之和,而是将隶属度的值相加,再除以总的记录数,所得到的值作为支持度。而对于含有多个属性的项集,隶属度按照其中值最小的属性进行计数,如表1和表2所示。
算法主要有剪枝和连接两个主要步骤:连接主要是根据频繁项目集产生新的候选项目集;而剪枝则是将候选项目集中不符合条件的项目集删除,主要是删除支持度小于最小支持度、含有同一模糊集属性以及含有非频繁项目子集的项目集。在模糊关联规则算法中,需要不断扫描原始数据库,来获取各个候选项目集的支持度。但随着关联规则挖掘的进行,原始数据中很多数据失去了使用价值,如此重复地遍历所有数据,势必降低算法效率。为此在模糊关联规则的基础上引入AprioriTid的思想,每一次扫描都生成一个新的事务数据库,新的数据库只包含上一次频繁项目集中的项目集属性和有意义的事务,下一次扫描只需要扫描上一次产生的新事务数据库,通过不断更新事务数据库,来减少事务数据库的规模,达到提高算法效率的目的。算法1:改进模糊关联规则挖掘算法。
输入:原始事务数据库T,每个属性项对应的隶属度函数集合F,最小支持度minsupport和最小置信度minconfidence。
输出:新事务数据库Dk,频繁项目集Lk。
第1步:对于T中各个连续型数据,根据对应的隶属度函数,计算所有数据的隶属度f。将求得的隶属度数据带入新的数据库中,记为D,此时D1就等同于D。
第2步:扫描D1数据库,将各个属性的隶属度累加求和再除以总记录数,计算所有属性的支持度,计算公式为:Support=(■1nf)/n;其中1≤y≤m(设D1共有m个属性、n条记录),减去支持度小于minsupport的项目集,形成L1频繁项目集,同时更新D1。
第3步:根据L1频繁项目集生成候选2项集,然后扫描D1数据库,同时生成D2新事务数据库,再计算各个“2-项集支持度”,然后支持度与minsupport比对,形成L2频繁项目集,同时更新D2。
第4步:根据L2频繁项目集生成候选3项集,剪掉含有非频繁子集以及含有同一模糊属性集的项目集,然后扫描D2数据库,生成D3新事务数据库,计算各个“3-项集的支持度”,再与minsupport比对,形成L3频繁项目集,同时更新D3。
第5步:重复生成候选项目集并剪枝,生成新的事务数据库以及生成新的频繁项目集,直到没有新的频繁项目集产生。
模糊关联规则挖掘算法在每一次产生候选项目集时,都需要扫描一遍初始事务数据库D,所得出来的项目集支持度结果对下一次查找并没有帮助。如果将每一次计算支持度过程中产生的数据保存下来作为新的事务数据库Dk,下一次计算候选项目集的支持度时,只需要扫描上一次新产生的事务数据库Dk。在k比较小的时候,由于候选事务集的数量大于原事务数据库属性数量,但随着对数据不断的挖掘,候选项目集数量会越来越少,同时由于很多事务不再包含候选项目集的任一属性而删除,事务的数量也会减少,所以新产生的事务数据库所包含数据数量会急剧减少,远远小于初始数据库D,扫描数据库所花费的时间会大幅减少。
四、基于改进模糊关联规则的学生课程成绩挖掘
1.方案设计
从学校教务系统抽出某年级一个学院学生在校期间成绩,导出数据源类型为Excel工作表,运用模糊关联规则挖掘算法,实验程序统一采用Python实现。主要目的是发现哪些课程之间存在着联系,基础课是否会对专业课产生影响,哪些课程会影响到后续课程等,由此对教学工作以及学生的大学学习进行指导。
2.数据预处理
(1)数据集成
将各个数据源数据都合并到一个表格中,对于类似课程都合并到一个课程名下,例如:“微积分Ⅰ”、“微积分Ⅱ”合并为“微积分”;Web开发基础、Web开发实战合并为“Web开发”。而合并后的课程数据,将采用类似课程成绩的平均数。对于研究内容没有意义的课程将被删除,例如军政训练、劳动实践等。以此来简化课程,减少挖掘复杂度,提高研究结果的可读性。
(2)数据清理
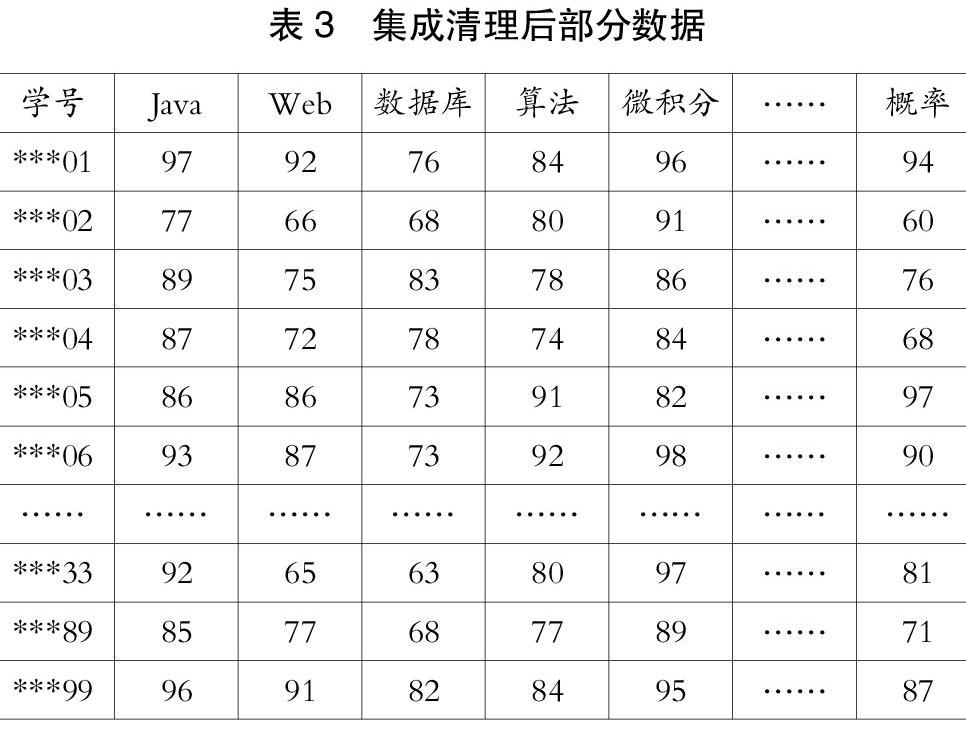
原始数据存在很多异常数据,很多学生由于缺考、取消考试资格、作弊等原因,成绩存在大量空缺项或异常项。需要将这些数据进行清除,以保证所有剩余数据都是有效的。清理后的数据如表3所示。
(3)数据转换
数据转换就是把学生成绩数据转换为统一的规格。根据模糊关联规则算法,由专家给出相应的隶属度函数,通过将成绩数据带入隶属度函数中,得出不同属性的隶属度,其中隸属度都是介于0到1之间的实数。结合实际教学经验,将学生成绩模糊处理为{high,medium,low},建立对应的隶属度函数,隶属度函数如图1所示。
根据对应的隶属度函数,对所有学生成绩数据进行转换,变成统一的格式,以便进行数据挖掘。转换结果如表4所示。
3.挖掘过程与结果
经过以上数据预处理,现采用改进的模糊关联规则挖掘算法对数据进行挖掘。最小支持度为0.2,最小置信度为0.7,最终得到频繁项集L4如表5所示。
根据最小置信度0.7,可以得到一些强关联规则集,如表6所示。
这些规则展示了一些专业课与基础课程之间的联系。例如:从表6第一条规则可以看出,微积分、概率论与数理统计、线性代数这些基础数学课的成绩在80多分或90多分的学生,算法分析与设计也会取得较高的成绩,有26.04%的学生满足这条规律,并且当微积分、概率论与数理统计、线性代数成绩都较高的情况下,算法分析与设计也较高的可能性为93.19%。可以看出微积分、概率论和线性代数等数学基础课的学习,对算法分析与设计有很大的帮助。第二条规则可以看出Web开发、算法分析与设计以及Java程序设计也存在一定的联系。由此在以后的教学工作中,就可以针对这些联系,进行适当的调整和安排,学生也可以根据这些规则合理安排学习生活。
五、结束语
本文对关联规则在教育大数据中的应用以及模糊关联规则算法进行了阐述,并提出了一种改进的模糊关联规则挖掘算法,对连续型属性进行模糊化处理避免了硬化划分破坏数据关系的真实性问题,优化了事务数据库,提高了扫描速率。通过对学生成绩进行分析,可以得出该算法能够较好地处理成绩数据柔性划分问题,并在处理数据时能够拥有较高的效率。分析获得的关联规则也能较为真实地反映课程之间的联系,为以后学校各种教学活动提供可靠的科学依据。
参考文献:
[1]周庆,牟超,杨丹.教育数据挖掘研究进展综述[J].软件学报,2015(11):3026-3042.
[2]Chan Man Kuok,Ada Fu,Man Hon Wong.Mining fuzzy association rules in databases,1998,27(1):41-46.
[3]陈池,王宇鹏,李超,张勇,邢春晓.面向在线教育领域的大数据研究及应用[J].计算机研究与发展,2014(S1):67-74.
[4]郑庆华,董博,钱步月,田锋,魏笔凡,张未展,刘均.智慧教育研究现状与发展趋势[J].计算机研究与发展,2019(1):209-224.
[5]苑森淼,程晓青.数量关联规则发现中的聚类方法研究[J].计算机学报,2000(8):866-871.
[6]邹晓峰,陆建江,宋自林.基于模糊分类关联规则的分类系统[J].计算机研究与发展,2003(5):651-656.
[7]R J Hathaway,JW Davenport.J C Baddc RdatBonaldialcf the c-means algorilhma Pattern Recognitkn 198ft 22(2):205-212.
[8]Agrawal R,SriKant R.Fast algorithms for mining association for mining association rules[C].Proceedings of the 20th international Conference on very large database.[s.1.]:M organ kaufman Pub inc,1994:487-499.
[9]Han Jiaweh Pei Jian.Yin Yiwen.et al.Mining frequent patterns without candidate generation:A frequent-pattern tree approach[J]. Data Mining and Knowledge Discovery,2004,8(1):53-87.
[10]张春,周静.动车组运维效率关联规则挖掘优化算法[J].计算机研究与发展,2017(9):1958-1965.
[11]申彦,宋顺林,朱玉全.基于磁盘表存储FP-TREE的关联规则挖掘算法[J].计算机研究与发展,2012(6):1313-1322.
[12]牛新征,王崇屹,叶志佳,佘堃.基于簇和阈值区间的高效关联规则隐藏算法[J].计算机研究与发展,2017(12):2785-2796.
[13]陈爱东,刘国华,费凡,周宇,万小妹,貟慧.满足均匀分布的不确定数据关联规则挖掘算法[J].计算机研究与发展,2013(S1):186-195.
[14]霍纬纲,邵秀丽.一种基于多目标进化算法的模糊关联分类方法[J].计算机研究与发展,2011(4):567-575.
[15]钟勇,秦小麟,包磊.一种基于多维集的关联模式挖掘算法[J].计算机研究与发展,2006(12):2117-2123.
[16]刘军煜,贾修一.一种利用关联规则挖掘的多标记分类算法[J].软件学报,2017(11):2865-2878.
[17]Hu Y H,Lo C L,Shih S P.Developing early warning systems to predict students online learning performance[J].Computers in Human Behavior,2014(36):469-478.
[18]Hu Yichung.Determining membership functions and minimum fuzzy support in finding fuzzy association rules for classification problems[J].Knowledge-Based Systems,2006,19(1):57-66.
(編辑:王天鹏)

