追根溯源 明晰错因
古作军


“轴对称图形”是初中数学的重要内容之一。一些同学在学习时,由于没有弄清知识概念的来龙去脉,对于知识概念理解不准,常会出现这样或那样的错误。下面就“轴对称图形”这一章的一些易错点进行剖析,希望能让同学们明晰错因,从而达到防止解题犯错的目的。
一、对轴对称图形的相关概念模糊不清
例1 下列说法中:①两个全等三角形合在一起是一個轴对称图形;②等腰三角形的对称轴是底边上的中线;③等边三角形一边上的高就是这条边的垂直平分线;④一条线段可以看作是以它的垂直平分线为对称轴的轴对称图形。正确的有( )。
A.1个 B.2个 C.3个 D.4个
【错解】C。
【错解剖析】轴对称图形的来源有二:一是一个图形沿着一条直线折叠,直线两旁的部分互相重合,这个图形是轴对称图形;二是把成轴对称的两个图形看成一个整体,这个图形是一个轴对称图形,而不是随意把两个图形合在一起。我们明确了这些,就可以断定①是错的。对称轴是一条直线,而等腰三角形底边上的中线是一条线段,二者属性不一致,所以它不能称之为对称轴,所以②是错的。垂直平分线的实质也是一条直线,等边三角形一边上的高是一条线段,所以③是错的。④的说法符合轴对称图形的定义,所以④是正确的。
【正解】A。
二、不能准确甄别轴对称图形
例2下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )。
【错解】A或B或C。
【错解剖析】轴对称图形具有如下特点:轴对称图形是一个图形;把这个图形沿着一条直线折叠,直线两旁的部分能够互相重合。只要明白这些,就会得出正确答案。
【正解】D。
三、对称轴寻找不全
例3如图1,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点。在田字格上画与AABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含AABC本身)共有( )。
A.1个 B.2个 C.3个 D.4个
【错解】B。
【错解剖析】直接利用已知图中已有的线段所在的直线为对称轴,只能找到两条对称轴,也就是说此时只能找到两个三角形。但是当我们把田字格的对角线连接起来时,对角线所在的直线也能成为对称轴,因此可得到第三个三角形。
【正解】如图2,得到的三角形有三个,所以选C。
四、错放变换后的位置
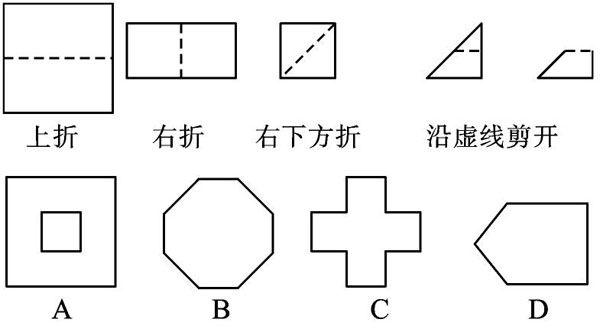
例4如图3,把一个正方形三次对折后沿虚线剪下,则所得图形大致是( )。
【错解】A。
【错解剖析】不能按照规定要求去操作,导致把剪下的位置弄错,从而出现错误的展开图。
【正解】C。
五、等腰三角形分类讨论不正确
例5 一个等腰三角形的两边长分别是3cm和7cm,则它的周长是____。
【错解】13cm和17cm。
【错解剖析】已知等腰三角形的两边,求它的周长。在不知道哪边是腰、哪边是底的情况下,我们要分两种情况讨沦,在每一种情况中还要注意验证能否构成三角形。
【正解】17cm。
例6 已知一个等腰三角形的两角分别是(2x-2)°、(3x-5)°,求这个等腰三角形各角的度数。
【错解】此题分两种情况:若(2x-2)°为顶角,得x=24,三角形的三个内角分别是46°、67°、67°;若(3x-5)°为顶角,得x=27,三角形的三个内角分别是76°、52°、52°。
【错解剖析】利用等腰三角形的性质解题时,易犯考虑不全面的这一典型错误。从表面上看,这道题分两种情况来计算,但实际上还有一种情况没有考虑到,即这两个角都不是顶角。
【正解】此题应该分三种情况。除了上述两种情况外,若(2x-2)。和(3x-5)。都不是顶角,则3x-5=2x-2,得x=3,三角形的三个内角分别是172°、4°、4°。
例7等腰三角形一腰上的高与另一腰所成的夹角为50°,则这个等腰三角形的顶角是____°。
【错解】40。
【错解剖析】等腰三角形的高可能在三角形的内部,也可能在三角形的外部。本题应分类讨论:等腰三角形的高在三角形的内部时(锐角三角形),顶角为40°;等腰三角形的高在三角形的外部时(钝角三角形),顶角为140°。
【正解】40或140。

