基于自适应滑模的多智能体系统容错一致性控制算法
葛志文,刘剑慰,王一凡
(南京航空航天大学, 江苏 南京 210000)
0 引言
近年来,随着多智能体在无线传感器网络[1]、编队控制[2]、多移动机器人[3]等多方面的应用,其协同控制问题已成为一个研究热点。多智能体协同控制的重要目标之一是一致性,即通过合适的控制方案,使所有智能体的状态趋于相同。根据是否存在领航者,多智能体一致性问题可分为两类:无领航者一致性和领航-跟随一致性。对于领航-跟随一致性问题,其主要目标是设计控制律,使所有跟随者状态与领航者的相一致。虽然目前对领航-跟随一致性问题的研究已经十分成熟,对二阶及高阶多智能体一致性问题的研究也均有涉及[4-5],但缺乏普遍性。为此,本文针对线性定常动态模型所描述的多智能体系统进行研究。
目前,已有多种方法应用于多智能体一致性控制中,比如最优控制[6]、自适应控制[7]及神经网络控制[8]等。滑模控制具有结构简单和对不确定性事物的强鲁棒性等优点,因此基于滑模控制的多智能体一致性问题受到诸多研究者的关注[9-11]:文献[9]设计了一种新型滑模面来解决非线性二阶多智能体的一致性问题;文献[10]基于滑模控制方法研究分数阶多智能体系统的一致性跟踪控制问题;文献[11]针对含有干扰的多智能体系统,将滑模控制和干扰观测器相结合,在有限时间内实现了多智能体的一致性。虽然上述文献采用滑模控制实现了多智能体的一致性,但其均未考虑由不连续控制所引起的系统抖振问题。为了实现连续滑模一致性控制,文献[12]提出了针对二阶多智能体的连续滑模一致性控制方法;然而,当多智能体系统由一般线性定常模型描述时,采用连续自适应滑模控制方法进行一致性控制的研究仍不充分。
多智能体系统能够实现一致性控制的前提是每个智能体都正常工作,但实际情况下,智能体的执行器可能出现故障,从而导致系统性能恶化[13],因此对出现执行器故障的多智能体系统进行容错控制具有重要意义。目前已有许多文献对多智能体容错一致性进行了研究:文献[14]采用自适应一致性控制算法解决了存在执行器故障和外部干扰的多智能体一致性问题;文献[15]基于自适应控制采用主动容错控制方式实现多智能体容错一致性;文献[16]提出一种容错协同控制算法解决了多智能体一致性跟踪问题。
在上述研究中,尽管滑模控制对外部干扰和执行器故障展现了良好的鲁棒性,但其在多智能体容错一致性方面的研究仍需深入。为此,本文针对存在执行器故障和外部干扰的多智能体系统,提出一种基于自适应滑模的容错一致性控制算法,其与文献[9-11]所用滑模控制方法相比,由于采用连续控制,故可解决系统的抖振问题;与文献[14-15]所提方法相比,其在结构上更为简洁,也更易实现;与文献[16]的容错跟踪控制算法相比,其可使多智能体系统更快实现一致性,并且对执行器故障具有更好的鲁棒性。
1 问题描述
本文首先引入图论知识描述多智能体间的信息交互,并以一个领航者与N个跟随者组成的多智能体系统为研究对象,描述其故障模型。
1.1 图论知识
在一个有向图中,如果存在一个根节点,其能沿某条路径到达任意节点,则称该图包含有向生成树。本研究中考虑含有一个领航者和N个跟随者的多智能体,其中领航者标记为0,跟随者分别标记为1, 2,…,N。跟随者间的通信拓扑由有向图的拉普拉斯矩阵L定义。领航者和跟随者之间的通信拓扑由对角矩阵G=diag(g1,g2,…,gN)定义:如果第i个跟随者-接收到领航者信息,则gi=1;否则gi=0。此外,用图表示包含领航者和跟随者在内所有多智能体的通信拓扑。
假设1图包含有向生成树。
引理1[17]图包含有向生成树,则矩阵(L+G)可逆。
1.2 系统描述
考虑一个由一个领航者和N个跟随者组成的多智能体系统,其中领航者的动态模型被描述为

式中:x0(t)表示领航者的状态变量,x0(t)∈Rn;u0(t)表示领航者的控制输入,u0(t)∈Rp;A∈Rn×n,B∈Rn×p,均表示给定矩阵;Rn表示n维范数空间;Rn×n,Rn×p表示矩阵。
第i个跟随者的动态模型被描述为
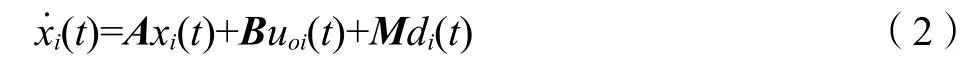
式中:xi(t)表示跟随者的状态变量,xi(t)∈Rn;uoi(t)表示跟随者的控制输入,uoi(t)∈Rp;di(t)表示外界干扰,di(t)∈Rp;M表示外界干扰矩阵,M∈Rn×p。
假设领航者无故障,第i个跟随者的执行器故障模型可被描述为

式中:ui表示设计的控制输入;ρi(t)和ri(t)分别表示执行器的部分失效和偏移故障,ρi(t)∈Rp,ri(t)∈Rp。
根据上述故障模型,第i个跟随者的动态模型可被改写为

则跟随者的状态方程为

式中:IN表示N阶单位矩阵;ImN表示mN阶单位矩阵;表示Kronecker乘积;ρ(t)=diag[ρ1(t),ρ2(t),…,ρN(t)]Im;。
为了方便后续控制算法的研究,对多智能体系统做出如下假设:
假设2执行器的部分失效故障、偏移故障和领航者控制输入是有界的,即存在正实数满足,,,其中表示范数。
假设3对于外部干扰,存在一个正实数,满足,i=1, 2,…,N。
假设4跟随者系统完全可控,且rank(B)=p,其中rank(·)表示矩阵的秩。
2 容错一致性控制器设计
本文根据跟踪误差设计积分滑模面,得到基于自适应滑模控制的多智能体系统容错控制器。
2.1 滑模面
在进行滑模面设计之前,首先定义跟踪误差:

式中:aij为权重邻接矩阵中的元素,表示跟随者i和j间的连接权重;gi表示第i个跟随者和领航者之间的连接权重。

式中:1N=[1, 1,…, 1]T∈RN。
则跟踪误差为

引理2[18]考虑由式(1)和式(2)定义的领航-跟随系统,如果有向图包含有向生成树且e(t)=0,则系统状态收敛并满足式(9)。

基于上述跟踪误差,设计如下积分滑模面:


2.2 自适应滑模容错一致性控制器
基于式(11)的积分滑模面为多智能体系统设计容错一致性控制律。含有不连续控制项的一致性控制律设计如下:
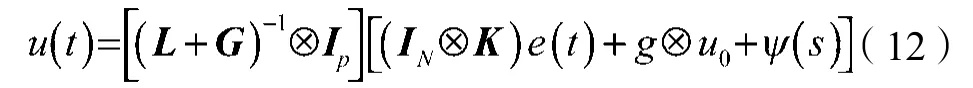
式中:ψ(s)为不连续切换增益,;g=[g1,g2,…,gN]T。
由于系统受到的外界干扰很难被准确测得,虽然可以选择足够大的切换增益ψ(s)来抑制干扰,但这会造成执行器严重抖振;同时,执行器故障的存在也加剧了系统的不稳定性,因此需要设计一种自适应控制律来抑制干扰同时处理执行器故障问题。
将本文的自适应增益设计为

式中:α,γ为自适应增益参数,α>0,γ>0。
式(12)中的不连续控制项ψ(s)的改进式为

式中:δ>0。
δ,βi由自适应律确定,则自适应容错控制律为
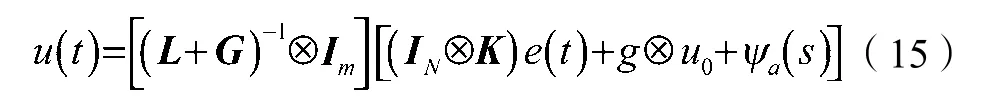
定理1针对存在执行器故障和外部干扰的多智能体系统,在加入式(15)所示的容错控制律后,跟踪误差在有限时间内有界稳定。
定义:
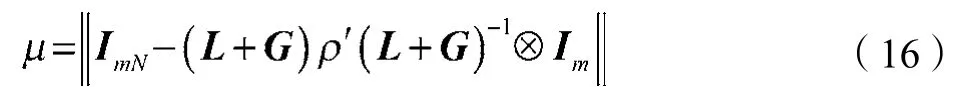
式中:ρ=diag(ρ1,ρ2,…,ρN),diag(…)表示对角矩阵。
由式(16)可知,0<μ<1。
证明:考虑Lyapunov函数

式中:为自适应增益的上界,且,其中,常数βc>0。
对Lyapunov 函数求导并代入式(15),得

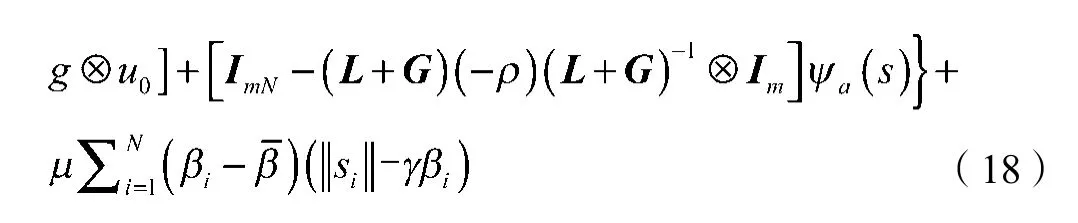
将式(16)代入式(18)可得:

下面分3种情况讨论Lyapunov函数的负定性:
(1)如果所有跟随者满足βi||si||≥δ,i=1, 2,…,N,则,可得


(2)如果所有跟随者满足βi||si||<δ,则,可得


(3)如果一部分跟随者满足βi||si||≥δ,另一部分满足βi||si|| <δ,可得

式中:ε1≤ε3≤ε2。
综上,对于任意的βi||si||,Lyapunov函数的导数满足
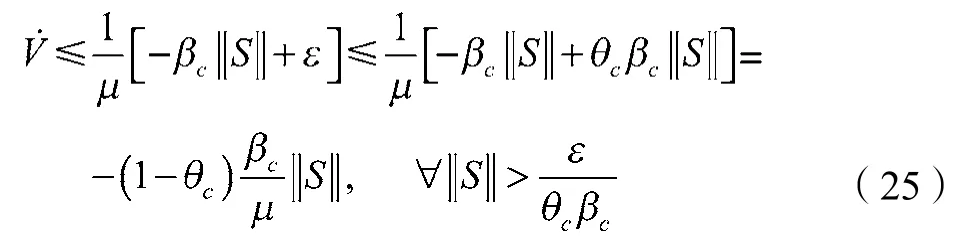
式中:ε=max{ε1ε2ε3}=ε2;θc为一常数,且 0<θc<1。
3 仿真分析
为了验证本文所提算法的有效性与优越性,本文对文献[20]中的四旋翼飞行器模型进行简化,得到四旋翼沿X轴方向运动模型:

式中:M表示重量;v表示速度;θ为偏航角;F为四旋翼推力。

式中:Km为正增益;ωm为执行器带宽;u为控制输入。引入执行器动态变量κ:

式(28)的状态方程为

根据式(26)~式(29),可建立X轴状态空间表达式:

式中:x,v,κ分别表示X轴方向位移、X轴方向速度和执行器的动态变量。
设定俯仰角弧度θ=0.035 rad,则根据文献[20]中的参数可得

领航者0和跟随者1,2,3,4的通信拓扑如图1所示。

图1 多智能体系统通信拓扑Fig. 1 Communication topology of the multi-egent system
其对应的拉普拉斯矩阵为

领航者和跟随者之间的连接权重矩阵为G=diag(0 0 1 1);外部干扰矩阵M=[0 0 1.5]T;外部干扰函数为di(t)=0.3sin(0.5it+0.25iπ),i=1, 2, 3, 4。跟随者执行器故障为ρ(t)=[0 0.2+0.1cost0 0.3+0.1sint],

领航者控制输入为u0=-K0x+0.1sin(t),其中K0=[0.0174 0.0309 -0.7333];领航者的初始状态为x0(0)=[2 0.3 0.1]T。
跟随者多智能体的初始状态为:x1(0)=[-1 0.1 0.15]T,x2(0)=[3 0.3 0.1]T,x3(0)=[1 0.4 0.25]T,x4(0)=[-2 0.3 0.2]T。
当跟随者存在执行器故障和外部干扰时,自适应参数选为α=150,γ=0.000 1,δ=0.9。根据上述参数进行数值仿真,图2和图3中仿真结果表明,跟随者在很短时间内就跟踪上领航者的位置和速度,不但实现了多智能体系统的一致性,而且能很好地处理外部干扰问题。

图2 自适应滑模控制方法下的位置跟踪轨迹Fig. 2 Position trajectory of the system under adaptive sliding mode control

图3 自适应滑模控制方法下的速度跟踪轨迹Fig. 3 Velocity trajectory of the system under adaptive sliding mode control
由图4、图5所示的位置和速度跟踪误差仿真曲线可知,即使跟随者2和跟随者4存在执行器部分失效故障,所有跟随者也能够在6 s内完成对领航者的跟踪;第7s时刻,跟随者1和跟随者3发生执行器偏移故障;第14s时刻,所有跟随者都发生偏移故障,跟踪误差曲线只有很小的抖动便快速收敛。由图6所示的自适应增益可看出,故障发生后,自适应模块能迅速对执行器故障做出响应。

图4 自适应滑模控制方法下的位置跟踪误差Fig. 4 Position tracking error of the system under adaptive sliding mode control
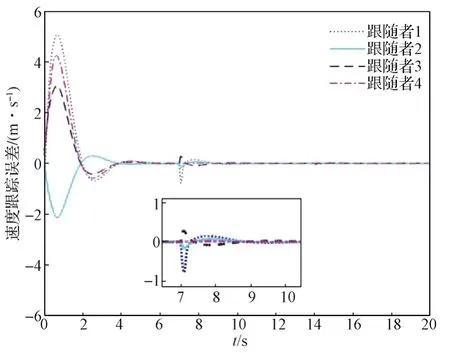
图5 自适应滑模控制方法下的速度跟踪误差Fig. 5 Velocity tracking error of the system under adaptive sliding mode control

图6 自适应滑模控制方法下的自适应增益Fig. 6 Adaptive gain of the system under adaptive sliding mode control
为了验证本文所提算法的优越性,使用相同系统参数和故障对文献[16]中的容错跟踪控制方法进行数值仿真,仿真结果如图7和图8所示。在执行器部分失效故障情况下,位置和速度跟踪误差都需要较长时间才能收敛;在发生执行器偏移故障后,误差曲线会产生较大波动。由上述分析可知,本文所提方案对外界干扰和执行器故障问题具有更优的控制效果。
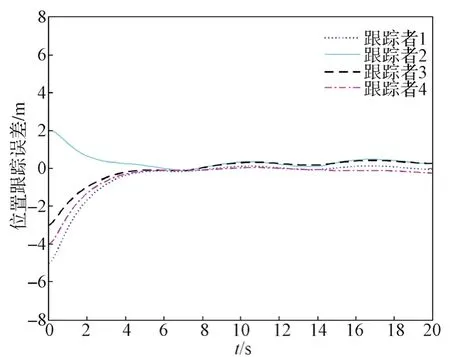
图7 文献[16]控制方法下的位置跟踪误差Fig. 7 Position tracking error of the system with the control protocol in literature [16]

图8 文献[16]控制方法下的速度跟踪误差Fig. 8 Velocity tracking error of the system with the control protocol in literature [16]
对图9和图10所示结果进行对比可知,连续自适应滑模控制很好地解决了系统的抖振问题。

图9 不连续控制方法下的滑模面Fig. 9 Sliding surface of the system under discontinuous control
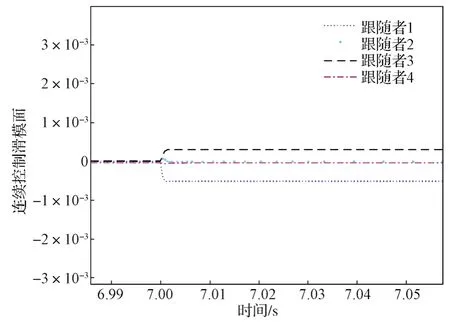
图10 连续控制方法下的滑模面Fig. 10 Sliding surface of the system under continuous control
4 结语
本文针对存在外部干扰和执行器故障的多智能体系统,提出了一种自适应滑模容错一致性控制算法,其在两种执行器故障及外部干扰情况下,能很好地实现多智能体系统的一致性,且比传统算法具有更优的容错控制效果;此外,连续自适应滑模控制律还解决了系统的抖振问题。后续,将对实际多智能体进行容错控制实验,这将是下一步研究的重点。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

