注重知识结构 引领深度学习——以《三角形中的范围问题》为例

□庞仕林

（杭州第四中学，浙江杭州310002）

指向深度学习的数学课主要是优化知识结构，改善陈述性记忆系统效能，使知识结构化、系统化、简约化，让学生减少遗忘，加强知识联系，培养知识迁移和转化化归能力，进而在深度思考中培养学生的数学核心素养.下面以《三角形中的范围问题》复习课的教学设计为例，谈一谈教学过程和思考.

一、以题引入 回忆旧知

教师的课堂设计就像电影的剧本一样，要拍出吸引人的电影，剧本一定要有吸引力.什么是“好剧本”呢？

首先，要有逻辑性，不能上下没有任何联系就横空出世，这样就容易让观众（学生）云里雾里，搞不清方向.比如，本节复习课前面就是以旧知为基础，通过演绎推理来解决问题，这样的复习就不仅仅是回忆知识点，而且能对知识点加深认识并且灵活运用.在此过程中学生明晰运算对象，选择正确的算法，算出结果，从而培养学生的核心素养.

课堂开始，请学生独立完成下面6道小题：

（3）在△ABC中，A=,B=，则C=_____________.

（4）在△ABC中，b2+c2-a2=bc,则A=_____________.

（5）在△ABC中，A=,b=1,c=2,则S△ABC=__________.

（6）如图1，在△ABC中，a=1,A=，则△ABC外接圆的半径R=__________.

图1

【设计意图】教师应为提升学生的认知水平而设计教学.本堂课教师帮助学生预备和激活知识，用简单题唤醒学生在本节课所用到的旧知，为学生对知识的灵活应用铺下台阶，从而进入深度学习.

其次，要有趣味性.进入深度学习，问题要从情感上让学生愿意接受，进而有探究的欲望.本节课交代问题研究的背景，从而勾起学生研究的欲望.

师：根据图2，请同学们对下面两个问题进行思考.

图2

问题1：已知两角一边，三角形能否确定？

问题2：已知一边一角，三角形能否确定？

问题背景：不定三角形.

【设计意图】用熟悉的问题引出研究的问题，交代问题背景，引起学生探索的欲望，使学生能够尽快进入角色，为进入深度学习打下情感基础.

最后，要有梯度，注意铺设的台阶数和台阶的高度，这个主要取决于学生的实际水平.对于层次低一点的学生台阶数尽量多一点，台阶高度尽量低一点；对于层次高的学生，台阶数可以减少，台阶的高度也可以高一些.题目可以设置多问，让学生一步步解决，最终解决最后一问，这样学生能够非常专注而且积极地投入到解决更复杂的问题中去.而深度学习向更高认知水平迈进，这一点在本堂课接下来例题设置的小问上能够体现出来.

二、一题多解 认识本质

将解答例题的方法用来解决类似问题，是对学生真正理解该方法的评价标准之一，也是进入深度学习的评价标准之一.深度学习强调学习内容的有机整合，把多种知识和信息进行联系，通过学生的同化和顺应，与原有的知识结构进行深度融合[1].所以在课堂上，我们要将例题中学生所学到的方法，通过变式，引导学生深入分析出几种不同方法进行解答，真正理解该问题的本质，使知识方法能够发生迁移.例如，在本堂课中的例题先用常用的代数方法，然后再用几何方法解释代数方法，使其了解问题的本质，进而能够进行方法的迁移.为后面研究已知一边及邻边问题，提供解决的策略.学生能够通过例题的研究方法解决该变式问题，形成方法的迁移，进而对该方法有深度的理解，从而对该方法能够灵活运用.

例1如图3，在△ABC中，角A,B,C所对的边分别为a,b,c,A=,a=，

（1）求角B的取值范围；

（2）求sinB+sinC的取值范围；

（3）求b+c的 取 值范围.

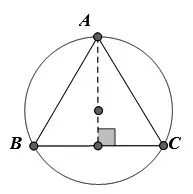
图3

生1：（1）0＜B＜.

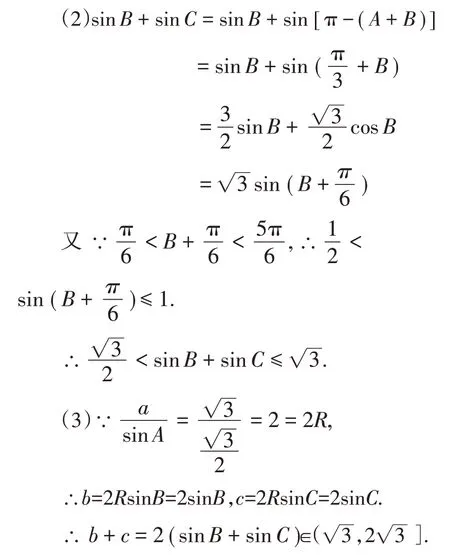
师：同学们，从上面计算过程来看，这两边之和取得最值时∠B的大小是多少呢？

生2：当∠B为时取最大值，而且此时△ABC为等边三角形，当∠B接近0弧度时，就接近最小值.

师：这位同学回答很正确，我们借助几何画板，直观来观察一下.

（通过几何画板移动A点位置，观察b+c的大小变化）

【设计意图】要求学生深度学习，题目设置必须是促进式的、层次性的、阶梯式的.这道例题设置了3问，层层相扣，前一问为后一问搭桥，难度层层递进，由简单到复杂.这道例题除了用代数的方法解之外，还要求用几何的方法求解，利用几何画板演示，通过展示发现A点运动到BC弧的中点时达到最大，从而直观地解释代数方法，揭示问题的本质，为知识迁移打下基础.

例2如 图4，在△ABC中，角A,B,C所对的边分别为a,b,c,,则△ABC面积的最大值是________.

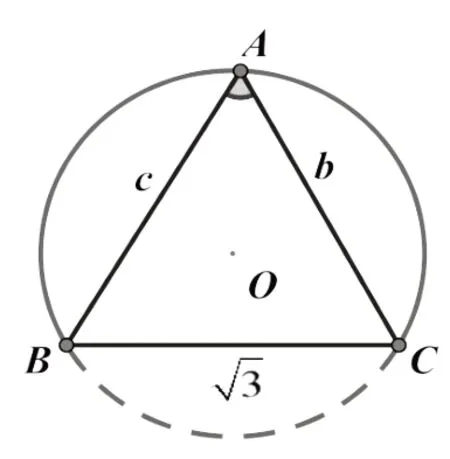
图4

生3：BC边不变，当A点到BC边上的距离达到最大值时面积最大，且A在半径固定的外接圆上运动，面积达到最大值时△ABC恰好为等边三角形，

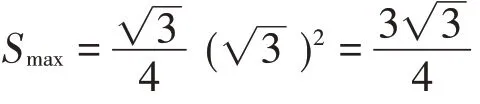
变式在△ABC中，角A,B,C所对的边分别为a,b,c,AB=,C=,求△ABC面积的最大值（如图5）.

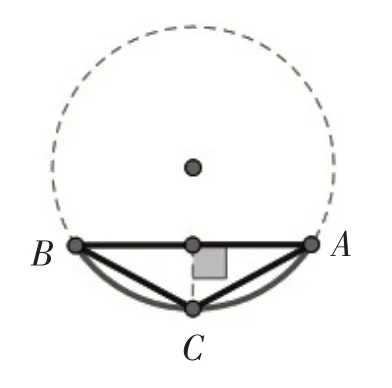
图5

生4：由画图可知，当C点在圆上转到离AB距离最大时面积达到最大，此时AB=AC，高h就为C到AB的距离，所以Smax=|AB|h=.

【设计意图】通过对问题本质的认识，将上题的求周长问题改为求面积问题，让学生进入一个看似新的环境，促使学生对内容的有机整合，让知识之间建立联系，以达到记忆深刻及能够迁移应用.变式将角度变为钝角，通过改变一个小条件，检测学生对上述方法的掌握，从而达到灵活运用几何方法的目的.必要时还可引导学生进一步理解，使之达到拓展水平.

三、问题拓展 知识迁移

授鱼还是授渔，数学思想和方法是数学知识在更高层次上的抽象和概括，它蕴含在数学知识发生、发展和应用的过程中，是数学知识转化为能力的桥梁[2].所以我们要授之以渔，就必须渗透数学思想方法，让学生领悟，进而能够达到融会贯通，举一反三之功效，这是进入深度学习的前提条件.笔者在本节课中，有意识地渗透数学思想方法，在例题中用图形来解释代数问题，体现数形结合的数学思想.另外在解决问题的过程中，将不熟悉问题转化为熟悉问题，这又体现了转化与化归的数学思想方法.正是有了这些思想方法的渗透，才使得知识迁移成为可能.

例3如图6，在锐角△ABC中，角A,B,C所对的边分别为a,b,c,B=,c=1,

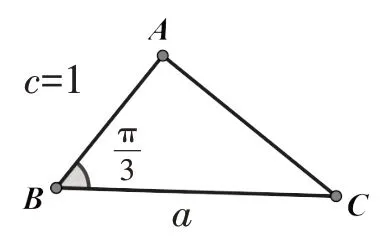
图6

（1）求角C的取值范围；

（3）求△ABC面积的取值范围.

生6：第（3）问，S=a，当越接近C角的最小值时，a边会越大.当越接近C角的最大值时，a边会越小，所以面积的取值范围为(,).

【设计意图】将问题条件由已知边及其对角迁移到已知一边及其邻角，求面积的最大值.学生通过前面的铺垫，已经具备解决该问题的方法，学生要解决这个新的问题需要将前面的知识和方法迁移过来，培养学生的创造能力，从而达到深度学习的最高认知水平.

四、总结提升 优化建构

深度学习着重学习过程的反思.所以一堂完整的课，总结是必不可少的.通过总结，可以使自身的知识建构得以圆满.

师：请同学们对本堂课的学习内容及解决问题策略进行总结.

生7：这节课主要针对的是三角形中的范围问题，并用几何法和代数法两种方法，从中我领悟到数形结合的解题策略和转化与化归的解题策略.

【设计意图】通过总结加深对方法的理解，同时也引导学生对知识建构反思，从而养成反思、调整、改造的良好习惯.

本堂课教学结构设计中的各板块联系紧密，先唤起本堂课所用到的旧知，再交代研究问题的背景，然后再对常见的定外接圆求角和边的范围问题求解，最后过渡到已知一角及邻边的不熟悉问题求解，实现知识的迁移.学生从熟悉问题向不熟悉问题探索，思维也逐步向高阶思维发展.发展学生的高阶思维，有助于实现深度学习.同样，深度学习也有助于高阶思维的发展.另外，教学提倡深度学习，要深挖教材内容的内涵，找出知识间的联系以及包含的数学思想方法，而且还需要根据学生的实际情况来安排内容.□◢