简易逻辑、计数原理、算法语言、二项式定理、复数、概率统计测试题B 参考答案

一、选择题

1.C 2.C 3.B 4.C 5.B 6.A 7.A 8.B 9.D 10.C 11.D 12.C 13.C 14.B 15.A

二、填空题

三、解答题

24.（1）命题p：关于x的方程x2+（a-2）x+4=0无解，则Δ=（a-2）2-16＜0，解得-2＜a＜6。

命题：q：2-m＜a＜2+m（m＞0），由于m=5，故-3＜a＜7。

由于“p∨q”为真命题，“p∧q”为假命题，故p真q假或p假q真。

当p真q假时，得无解。

当p假q真时，得得-3＜a≤-2或6≤a＜7。

综上所述，实数a的取值范围是（-3，-2]∪[6，7）。

（2）当命题“若p，则q”为真命题，“若q，则p”为假命题时，可知命题p为命题q的充分不必要条件。

所以命题p表示的集合A={a|-2＜a＜6}是命题q表示的集合B={a|2-m＜a＜2+m（m＞0）}的真子集，所以有解得m≥4，当m=4时，A=B，故m＞4。

所以实数m的取值范围是（4，+∞）。

（2）第5次测试的产品恰为最后一件次品，另3件在前4次中出现，从而前4次有一件正品出现，所以共有不同的测试方法。

26.（1）X的所有可能取值为0，1，2，3，4，5，6。依条件可知）。

所以X的分布列如表1所示：

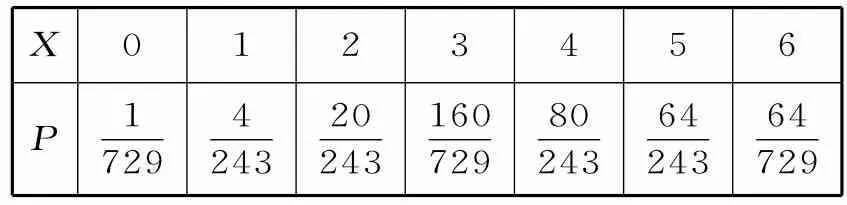
表1

（2）设教师甲在一场比赛中获奖为事件A，则即教师甲在一场比赛中获奖的概率为。

27.（1）根据列联表中的数据可得K2=所以在犯错误的概率不超过0.05的前提下不能认为获得“运动达人”称号与性别有关。

所以X的分布列如表2所示：

表2

②因为σ2=0.25，所以σ=0.5，所以μ+σ=6+0.5=6.5，μ-σ=6-0.5=5.5。

由①知，一件搪瓷水杯等级系数X位于区间（5.5，6.5）内的概率为0.6826。

依题意知Y～B（10000，0.6826），所以E（Y）=10000×0.6826=6826。

（2）A厂生产的搪瓷水杯更具有可购买性，理由如下：

将频率视为概率，可得B厂生产的搪瓷水杯的等级系数X2的概率分布列如表3所示：

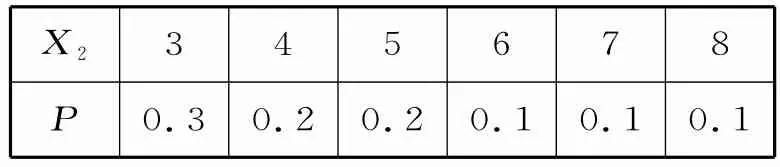
表3

所以E（X2）=3×0.3+4×0.2+5×0.2+6×0.1+7×0.1+8×0.1=4.8，即B厂生产的搪瓷水杯的等级系数的数学期望等于4.8。

因为A厂生产搪瓷水杯的等级系数的数学期望等于6，价格为36元/件，所以LA=。

因为B厂生产的搪瓷水杯的等级系数的期望等于4.8，价格为30元/件，所以LB=。