基于身份的动态层簇式无线传感网络认证算法

袁 驰

（中国人民大学信息学院，北京 100872）

（∗通信作者电子邮箱chiyuan@ruc.edu.cn）

0 引言

常规的密钥管理算法中以公钥密码基础最为常见［1-3］，这种密码体制可分为三大类：基于公钥证书的密码体制、基于身份的密码体制、无证书密码体制［4-5］，其中基于身份的密码体制无论是在安全性或是计算复杂度上相对优势都较为明显［6］。文献［7］指出，基于身份密码体制（ID-Based Cryptosystem，IBC）是最适合无线传感器网络（Wireless Sensor Network，WSN）的公钥体制。但是基于身份体制有一个致命的缺陷就是密钥托管问题，因为私钥生成中心掌握着所有用户的私钥，它可以非常容易冒充任何节点用户，私钥生成中心可以解密任何用户密文，可以伪造用户签名，并且不易被发现。因此，如何设计出既能充分利用各节点的身份信息从而简化密钥管理开销，又能避免私钥生成中心带来的密钥托管问题的安全认证算法，就成了无线传感器网络信息安全需要研究的一个重要问题。近年来，学者们针对此问题提出了各种解决方案，但多数方案仍然依靠私钥中心（PRivate Key Generator，PRKG）来生成用户私钥，因此并没有从根本上解决密钥托管问题。

针对此，提出的基于身份的分簇认证算法（Identity-based Dynamic Clustering authentication algorithm，IDC）算法，抛弃私钥中心，引入一个可信第三方公钥中心（Key Generating Center，KGC），直接产生用户公钥（与无证书密码体制使用公钥中心和用户共同产生用户私钥完全不同），从根本上解决了密钥托管问题，还可以动态生成全局伪秘密、能耗较低、性能稳定并且安全性好，非常适合WSN环境。具体特点如下：

1）没有密钥托管问题。IDC 算法结合椭圆曲线离散对数困难问题、哈希函数、解签密等知识，与传统的基于身份认证算法中由私钥生成中心生成所有用户私钥不同，它利用一个公钥生成中心，采用逆向思维方法，生成申请者的公钥及其对应的验证参数，发送给申请者验证，而用户的私钥既不由公钥中心生成，也不用和公钥中心联合生成（区别于传统无证书系统），而是由用户自己秘密选定。

2）算法拥有较低的计算、存储量但安全性较高。IDC 算法同时考虑到WSN 的特性，首先，采用分层结构，将各群体分为不同的簇群；采用分级结构，将系统分为簇首层（Cluster-Head Layer）和内部层（Intra-Cluster Layer）。由基站（Base Station，BS）为每一个簇首统一编发Id 号，由簇首层身份信息构成身份信息矩阵ID（Identity-matrix），内部层节点身份信息不参与身份矩阵构成。其次，在分层结构的基础上，又有针对性地采用了分级处理，针对BS、簇首、普通节点能量的差异，采用两种不同的公钥生成算法：簇首层（顶层）公钥申请过程基于身份矩阵运算，而内部层（下层）节点公钥申请基于身份Id 与哈希函数数学运算得出。第三，身份Id 信息在算法中得到充分应用，与算法结合紧密：由Id 信息生成的范德蒙矩阵，大大节约了存储空间，同时也减低了计算量；由Id 信息产生单向多项式的各系数，用以产生动态伪秘矩阵，无需再采用随机数等方式生成多项式系统，也降低了计算量；动态伪秘矩阵也使得算法的安全性大大提高。

3）结合WSN 环境特点，节点间认证采用一次（解）签密方案，降低了通信能耗。IDC 算法采用一次（解）签密方案，在一次通信过程中同时实现加密和认证功能（一次通信是相对于一个节点的（解）签密过程而言，不考虑节点认证成功后的反馈信息或不成功的返回信息），极大地节省了资源。

需要指出的是，提出的IDC 算法，在解决了由私钥中心带来的密钥托管问题的同时，引入了公钥中心KGC，产生了一个新问题，就是合谋攻击问题，即由若干节点合谋，对公钥中心掌握的全局秘密D 进行破解的问题。对此，本文引入了身份Id 单向多项式，动态生成伪秘密矩阵D'，可以杜绝合谋攻击，保证了算法的安全性。

1 相关工作

1.1 基于身份的认证体制

较为典型的基于身份认证算法有秦志光等［8］提到的密钥隔离密码系统（Key-insulated cryptography），将密钥分成两个部分，一部分由用户自己控制，另一部分由一个物理安全的协助者保存。在需要使用密钥时将两部分的密钥进行“拼接”从而得到一个完整的密钥；但其没能利用有效各节点的身份信息。陈渊等［9］提出一种基于身份但无线性对运算的加密算法，并在随机预言机模型下证明了算法是适应性选择密文安全的。两种算法都采取一定方法避免了计算量较大的对运算操作，节省了开销。但是两种算法都借鉴无证书的思想，节点的私钥由节点和私钥生成中心（PRKG）共同生成，而非节点自己单独生成，因此这两种算法并没有真正解决基于身份体制中的密钥托管问题。危蓉等［10］提出了一种基于身份的WSN层簇式密钥管理算法，较好地解决了WSN 密钥管理问题，算法运用身份认证加密技术，对节点认证后进行分簇，并建立簇成员与簇头之间共享簇密钥，实现了系统构建、签名、加密一体化，并通过分析对比，验证了算法可以保证簇内完全连通并满足无线传感器网络各项要求；但其采用椭圆曲线的Weil 双线性对运算却使得算法运算量增大。

郭江鸿等［11］提出了一个新的无线传感器网络密钥协商算法，有效地解决了传感器网络密钥协商方案中双线对运算能耗较高且耗时较长的问题，但其算法描述系统公私钥对是预先设定，在其广播阶段并没有将系统私钥x 广播，而在节点间相互通信之初却直接利用了系统私钥x，其算法并未说明x 是何种方式秘密传送至各节点，而系统私钥x 如何有效分发正是此类算法一个关键环节，因此此算法虽然有一定创新但是回避了一个重要问题，仅是理论可行。郭萍等［12］将基于身份的RSA 机制与轻量级（Certificate Authority，CA）思想相结合，构建了一个基于身份及轻量级CA 混合模型的传感器网络密码算法（简称LCA）。但这两种算法的计算量与通信量均较大，仍然需要改进。

Yuan 等［13］提出一种（Authentication of Vandermonde Matrix，AVM）认证算法，利用矢量的正交空间内积与张量积特征，采用复杂度较低的矩阵相加（D+）方法来构建密钥，保证了算法的前向安全性。另外，引入了随机数与零知识证明算法，算法的不可逆性得以提高，使得攻击节点不能篡改和替换消息，有效杜绝了中间人攻击。

1.2 分簇管理

李英磊等［14］提出一种动态分簇的密钥认证算法，对节点能量消耗和网络安全性作出分析，给出了相关的解决办法；Rohbanian 等［15］提出了层簇式WSN 进行密钥管理，首先构建最短路径，使用基于椭圆曲线的密码方案进行会话密钥分发；董发志等［16］提出一种“集中分簇，分布簇头选举”的算法，综合考虑节点能量、距离等因素，达到了较好的能量和安全性的平衡；邓绍江等［17］提出采用网络分化思想提高系统通信效率，利用分组加密算法EBS-GL（Grouping and Layered key management strategy in WSN based on Exclusion Basis System），通过汇总消息比对方法及奇异点排除策略进行认证，增强了系统可恢复性；危蓉等［10］提出的算法也属于分簇管理研究范畴。

2 算法设计

2.1 基本思想

2.1.1 动态安全过程

由用户密钥生成过程可知，公钥中心在生成两个集合B1和B2后利用B2产生公钥中心验证参数Kij，将B1=｛bj0，bj1，…，bjn｝发送至申请簇首用于生成Kij，分析部分矩阵［D'ID］T如式（1）所示（为表示方便，用“(B1)i”表示第i个簇首申请者得到的公钥中心返回集合）：

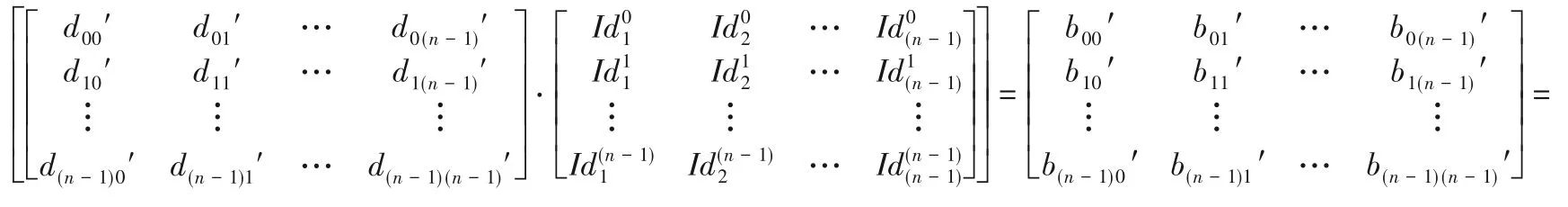
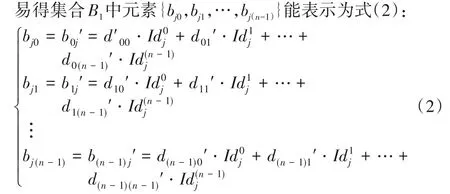
如果不引入伪秘密矩阵D'，由秘密矩阵D 直接参与簇首节点的申请过程验证，由于秘密矩阵D 为对称矩阵，易得(n*n)的D 有个独立的矩阵项，而集合B1会多次以固定的系数（dij）计算出结果返回给相应节点，这必然会导致相应个数节点的合谋攻击，从而使攻击者得到全局秘密矩阵D。

2.1.2 合谋攻击条件

设全局秘密矩阵 D 中元素 dij为未知数xij，且有i，j ∈{0，1，2，…，(n -1)}，则对于每一个簇首申请节点而言，均可以得到一个如式（3）的线性方程组：

这些线性方程组的每一行中的未知数xij均相同，因此可以分别取各线性方程组的相同行（以第1 行为例），组成新的线性方程组，进而可反推出全局秘密D的对应行元素，最终破解全局秘密矩阵D，如式（4）所示：

2.1.3 应对策略

本文引入伪秘密矩阵D'，矩阵元素由一个单向函数多项式计算得出，分析多项式易知，由霍纳法则（Honer’s Rule）通过不断地把x作为公因子从降次后的剩余多项式中提取出来：

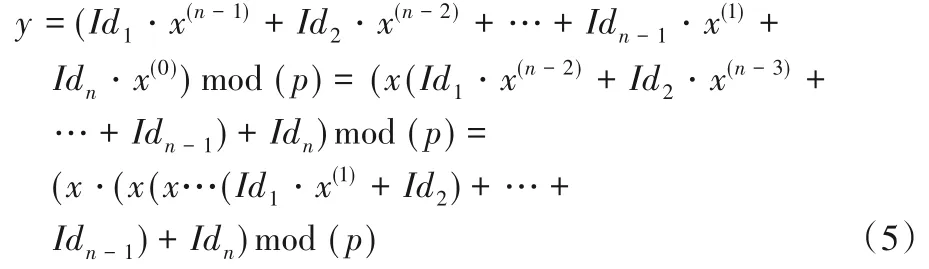
过程如表1所示。

可以看出，在已知x，Idi和p的情况下，非常容易求得y；而反过来，在已知y，Idi和p 的情况下，想求得x，则至少需要n2(lb p)2次乘法，当n 及p 很大时，可知由y 求x 几乎不可能。由分析可以看出，引入伪秘密矩阵D'有两个好处：

一是各伪秘密矩阵D'能保证动态变化。对于不同的簇首申请者，公钥中心都会根据不同的申请者验证份额Vi=（Vx，Vy）中的Vx（p=Vx）生成相应的伪秘密矩阵D'，因此不同的D'中对应的元素d'ij也各不相同。

二是单向函数y=f(x)能保证算法的前向安全性。即便是攻击者通过其他手段，得到了伪秘密矩阵D'中的元素d'ij，其想实现由d'ij推算出秘密矩阵D中的元素dij也几乎不可能，从而杜绝了各不同的簇首申请者合谋攻击。

表1 计算过程Tab.1 Calculation process

2.2 外部通信（簇首间）

2.2.1 系统初始化

定义网络中无线传感器簇数目为n，每个簇首赋予一个特定的数字作为其身份标识，即簇首节点集合为｛Id1，Id2，…，…，Idn｝，公钥中心首先进行如下操作：

步骤1 选定素数q，由此确定循环群Gq，之后选取此循环群上的椭圆曲线E，G为基点，p为其阶。

步骤2 选取公秘矩阵D 并秘密保存，D 必须满足是（n×n）对称矩阵。

步骤3 构造两个哈希函数：

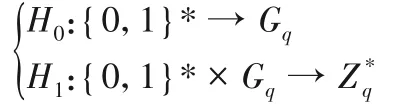
步骤4 构建簇首身份范德蒙矩阵ID。

步骤5 依据簇首节点集合产生一个单向函数多项式，如下：

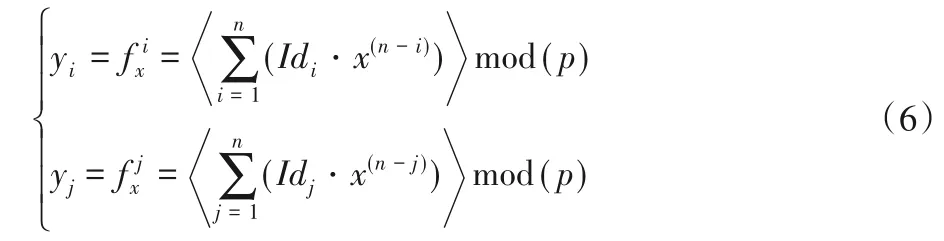
根据不同的簇首节点产生不同的伪秘密矩阵元素。

步骤6 公钥中心对簇首层广播循环群Gq、椭圆曲线E、基点G、哈希函数H0和H1。

2.2.2 用户密钥生成

步骤1 由申请者选取椭圆曲线上某一点P（xi，yi）作为自己的私钥，即Si=（xi，yi）；同时随机选取数zi∈Ζ，计算得出用户的验证份额Vi=ziSi=(Vx，Vy)。

步骤2 申请者秘密保存随机数zi（用于随后通信过程中的签密过程），把自己的验证份额Vi连同身份信息Idi合并得［Vi‖Idi］一并发送至公钥中心（随机数zi不能发送给公钥中心，以防止公钥中心泄密，zi仅用于随后簇首间通信）。

步骤3 公钥中心收到信息后，利用单向函数多项式y=f(x)mod(p)和秘密矩阵D中元素dij，产生一个伪秘密矩阵D'中元素（为了保证每一个簇首节点对应不同伪秘密矩阵，需要取申请者的验证参数参与到单向函数多项式的计算中，即有，如下：

从而得伪秘密矩阵D'。

步骤4 公钥中心在身份范德蒙矩阵ID 中随机选取一列，比如j列，与上步生成的伪秘密矩阵D'联合，计算集合B1=并由此计算出用户Idi的公钥Pi=G ⋅Vi及公钥中心的验证参数Kij=

步骤5 公钥中心发送用户公钥Pi，集合B1及验证参数Kij至申请者。

步骤6 申请者收到公钥中心返回的信息后计算Kji=并验证是否等于上步计算的Kij：如果通过，则申请接受公钥Pi，并秘密保存自己的私钥Si，同时公钥中心对外公布用户公钥Pi；否则，返回错误，申请失败，输出符号⊥。

至此，完成各簇首节点的公私钥的配置。

2.2.3 签密

身份为Idi的节点为了给身份Idj的簇首节点发送一个消息Msg，执行以下步骤：

步骤1 Idi首先取公钥申请阶段秘密保存的随机数zi，与椭圆曲线上的基点G 计算ziG=R（r1，r2）；之后取r1与簇首Idj的公钥Pj计算得验证参数（u，v）=r1×Pj；再用u对消息Msg加密得Ecr=Eu(Msg)。

步骤2 利用哈希函数计算参数M=H1(r1‖Ecr)，参数N=H0(k1M)G。

步骤3 计算参数O'=Si-H0(r1M)mod q，参数O=M +O'。

步骤4 Idi将秘密保存的随机数zi与上述各参数，生成密文Ci=(Ecr，R：(r1，r2)，N，O，z)，发送至Idj。

2.2.4 解签密

簇首节点Idj接收到密文Ci后，执行以下步骤：

步骤1 首先提取节点Idi的R 的前半部分r1，与自己的公钥Pj计算验证参数U'=r1Pj=(u，v)。

步骤2 计算M=H1（r1‖Ecr），O'=O-M。

步骤3 用u对加密消息Msg解密得到Msg=Du(Ecr)。

步骤4 计算P'=N+O'G，并验证（zi·P'）？=（Pi）：如果验证二者相等，则簇首Idi与Idj的共同的通信密钥即为u，同时接受明文Msg，之后将v 保存，作为簇内共享密钥；否则验证失败，输出符号⊥。

至此，完成簇首之间通信。

2.3 簇内通信

2.3.1 簇内密钥对申请

在每个簇内通过上述簇首节点解签密过程预置对称共享密钥v。簇首为Idi的簇内节点Idim需要申请自己的公私钥对。按如下步骤：

步骤1 节点Idim选取随机数rm，与簇共享密钥v（由上述簇首层运算得出）相乘之后发送［rm‖v（Sm）‖Idim］至簇首Idi。

步骤2 簇首Idi选取随机数rn，依次计算两个参数P1=rnSm-H0(Idim)，P2=rn+H0(Idi)H0(P1Idim)。

步骤3 簇首Idi计算节点Idim的公钥Pim=G·Sm，之后发送密文Ci=(P1，P2，H0(Idi))至簇内节点Idim。

步骤4 节点Idim计算P2Sm的值是否等于P1+H0(Idim)+rmH0(Idi)H0(P1)的值：如果相等，则申请者接受公钥Pim，并秘密保存自己的私钥Sm，同时簇首Idi对外公布簇内用户公钥P1；若不相等，则返回错误，申请失败，输出符号⊥。

至此，完成各内部节点的公私钥的配置。

2.3.2 簇内解签密

簇内各节点申请完密钥对后，按上述簇首解签密过程进行签密与解签密，在此不再重复描述。

3 性能分析

3.1 安全性证明

定理1可验证性。在簇首层（Cluster-Head Layer）公钥中心和簇首Idi按照上述用户密钥生成步骤进行公钥申请，验证若Kji=Kji，申请者接受分配公钥的过程满足算法正确性要求。

证明 首先将2个矩阵伪秘密矩阵D'和簇首身份信息矩阵ID）进行乘和转置运算：

而在用户密钥生成步骤中，公钥中心随机选取的第j 列，与伪秘密矩阵D'联合，计算集合B1=｛bj0，bj1，…，b（jn-1）｝和集合

由上述过程可以看出，2 个矩阵（伪秘密矩阵D'和簇首身份信息矩阵ID）运算后得到的新矩阵K 仍然是对称矩阵，对于矩阵K 中的元素来说，均有Kij=Kji。因此公钥中心公钥分配过程满足正确性要求。 证毕。

定理2不可否认性。上述簇间通信过程中的簇首间验证参数Pi的再计算过程满足算法正确性要求。

证明

因为O'=Si-H0(RiM)mod q，N=H0(RiM)G

所以P'=N+O'G=N +(Si-H0(RiM)mod q)G=H0(RiM)G +(Si-H0(RiM)mod q)G=Si⋅G

因为Pi=Vi⋅G，Vi=zi⋅Si

所以Pi=zi⋅Si⋅G=zi⋅P' 证毕。

3.2 抗攻击性

IDC 算法中，申请者的私钥由申请者自己秘密保存，公钥中心生成的是申请者的公钥，在通信过程中传递的验证参数也是基于申请者的公钥，即使某一节点被捕获，并不会对算法的机密性产生影响。其次，由于伪秘密矩阵D'的引入，实现的全局秘密的动态生成，敌手难以对伪秘密矩阵D'进行破解，而由dij'到dij的单向性质更加巩固了这种假设，说明算法的抗攻击（合谋攻击）性得到了保证。

初始化配置完成后，某一簇首申请者通过基于身份矩阵的方法申请自己的公钥，在申请成功后拥有自己的私钥si和由公钥中心分配的公钥Pi，之后通过和同级另一簇首相互签密从而获得共同的通信密钥u，因此，IDC 算法采用矩阵D 作为公钥中心的全局秘密，结合动态伪秘密矩阵D'实现申请者公钥生成，要比传统基于身份的认证系统中用简单数字或哈希函数等作为全局秘密要更为安全。

注 簇内通信过程中簇首与普通节点的申请过程与解签密过程相似，唯一不同点在于簇内普通节点申请过程不是基于身份矩阵，而是基于身份Id 与哈希函数的数学运算得出，这样做是为了降低簇内节点的计算量和存储量，但二者生成密钥对的思路相同，只是形式有差别，故此安全分析仅选择簇间就可说明问题，簇内不再假设。

3.3 模拟实验

3.3.1 场景设置

本文仿真实验环境搭建参考CMU 大学MONARCH 项目（CMU Monarch Projects Wireless and Mobility extension）［18］提出的multihop无线网线模拟实验所用方法。分3个步骤：一是修改并新增protocol 代码文件*.cc 和*.h；二是对packet 头文件*.tcl 和*.h 进行修改，同时对参数文件ns_default.tcl 进行定义；三是对makefile文件进行修改。

利用方法中的Setdest 程序随机生成规模为60 的WSN 场景，相关参数的设置具体有三块：

第一块是网络性能方面，如表2所示。

第二块为各比较算法能耗量化设置，对算法AVM、EBSGL、LCA与IDC算法进行能耗和时耗比较。具体如表3所示。

第三块为可变量固定场景设置。由于在AVM 算法、LCA算法中的参数N1、L1、N不是固定的长度，其选取数值不同会导致计算能耗差异，因此需要对其进行固定操作。文献［1-2］中证明的RSA模数值最低安全保证长度值与阈值的最优典型设置域，本文将实验场景设置为6个，具体为：S1（N1，L1，N）：（256，64，1 024）；S2：（256，128，1 024）；S3：（512，64，1 024）；S4：（256，256，2 048）；S5：（1 024，256，2 048）；S6：（2 048，128，2 048）。通过编写tcl 脚本定义出相应的通信过程，使用SET 命令对场景进行设置，包括网络的模拟结构以及通信过程，之后通过tracefd文件记录模拟过程的跟踪数据。

表2 网络性能参数设置Tab.2 Performance parameter settings of the network

表3 四种算法计算量对比Tab.3 Comparison of calculation amount of four algorithms

3.3.2 实验对比

图1和图2给出了四种算法的能量消耗与时间消耗对比，总体看来，IDC算法在能量消耗与时间消耗方面均优于其他三种算法。可以看出，在完成一轮最小粒度的通信过程中，IDC算法能量消耗达到了毫焦耳（mJ）级，时间消耗基本接近毫秒（ms）级，均远优于LCA、AVM、EBS-GL算法，充分说明IDC算法的优势。原因有：1）因为IDC算法在满足上述安全需求的情况下，针对节点所处位置的不同及运算能力的差异，采用分层分级方法，在减少系统存储量的情况下同时提升了算法的处理效率。2）因为IDC 算法采用的一次解签密方案即实现了节点间的认证及公密生成，大幅降低了通信成本，通信资源开销也因此变少。3）因为公钥中心的核心秘密身份矩阵是由身份Id生成的范德蒙矩阵，矩阵的每一列元素都可以唯一生成，在节省存储空间的同时也降低了算法计算复杂度。

其次，IDC 算法性能稳定。由图1 可以看出，从S1场景到S6场景（L1：64→128，N1：256→2 048）的变化过程中，IDC 算法在完成一次单精度乘法的耗时始终处于一个比较平稳的水平，即能量消耗在1～10 mJ，跨度不大于1.3 mJ；时间消耗一直保持在0.002～0.006 s。而LCA 等算法在场景S3到S4的变化过程中，出现了比较大的波动。特别地，在S3场景下，新算法耗时0.003 s，而LCA 算法耗时接近0.1 s，新算法的效率要高出其将近30 倍，如图2 所示。这就表明IDC 算法在传送的信息比特位长度值变化幅度较大的情况下，具有较强的稳定性。

图1 四种算法的能耗对比Fig.1 Energy consumption of four algorithms

图2 四种算法时耗对比Fig.2 Time consumption of four algorithms

4 结语

无线传感器网络是一种非常有应用前景的传感器网络。由于其自组织的网络特点，设计出安全且低能耗的轻量级通信协议尤为重要。本文提出的基于身份的IDC认证算法，由公钥中心生成申请者的公钥，由用户自己秘密选定私钥，从而避免了基于身份认证算法的密钥托管问题。同时，算法采用分层结构和分级处理，增强了簇间通信的安全性，降低了簇内节点的计算量和存储量。通过实验对比，新提出的IDC算法能够保证网络通信安全，并且具有低能耗和高稳定特性，非常适合于WSN。由于目前国内外对研究对真实环境下的实际实验测试工作研究还很薄弱，而本文所提到的实验环境也仅是利用仿真软件进行人为设定，证明了算法的理论可行性，但缺乏在实际环境下的演练测试，所以下一步工作的重点除了对算法本身的性能研究之外，将尝试在真实环境测试所研究的算法。