独立性检验的基本思想及其初步应用

张艾楠

一、教学目标：

1.通过生活中实际问题的探究，理解独立性检验的基本思想，明确独立性检验的基本步骤，会对两个分类变量进行独立性检验，并能利用独立性检验的基本思想来解决实际问题。

2.通过探究高中生选修物理与性别是否有关系引出独立性检验的问题，借助样本数据的列联表分析独立性检验的实施步骤。

3.通过本节课的学习，加强数学与现实生活的联系。以科学的态度评价两个分类变量有关系的可能性。培养学生运用所学知识，解决实际问题的能力。教学中适当地利用学生合作與交流，使学生在学习的同时，体会与他人合作的重要性。

二、教学重点：

通过案例的分析研究，展现统计中数据分析的全过程。让学生体会独立性检验的基本思想，掌握独立性检验的一般步骤;

三、教学难点：

独立性检验过程中 的获得及其意义的理解。

四、教学方法：

问题化和探究式教学

五、教学手段：

多媒体，pad

六、教学过程：

（一）创设情境

课前预习（小组讨论，合作探究）：

在之前的学习中，我们研究过两个变量的相关性及它们之间的线性回归方程。这里再给出几个例子，吸烟与患慢性气管炎是否有关？秃顶和患心脏病是否有关？爱好运动与性别是否有关？上述例子中的各个变量与之前学习过的变量不太一样，变量吸烟我们可以按吸烟与不吸烟分类，性别我们可以按男女分类，变量的不同值表示个体所属的不同类别，像这样的变量，我们叫分类变量。分类变量不一定只能分两类，比如职业，这个变量就有很多的结果，高中阶段我们只研究具有两个结果的分类变量。观察下面这个例子：

为了迎接2020年的新高考改革，在高一下学期的时候对全年级的761名学生选修物理、化学、生物、政治、历史和地理的情况进行了调查，这里给出全年级同学选修物理的情况。请同学们自己整理数据并回答下列问题。

问题1：你能否设计一个方法，使得上述的统计结果更加直观？

问题2：你能否设计出一个方案，来判断高中生选修物理是否与性别有关？

问题3：请同学们以小组为单位，搜集你们感兴趣的分类变量的相关数据，并用你设计的方案来判断你所研究的分类变量之间是否存在一定的关系。

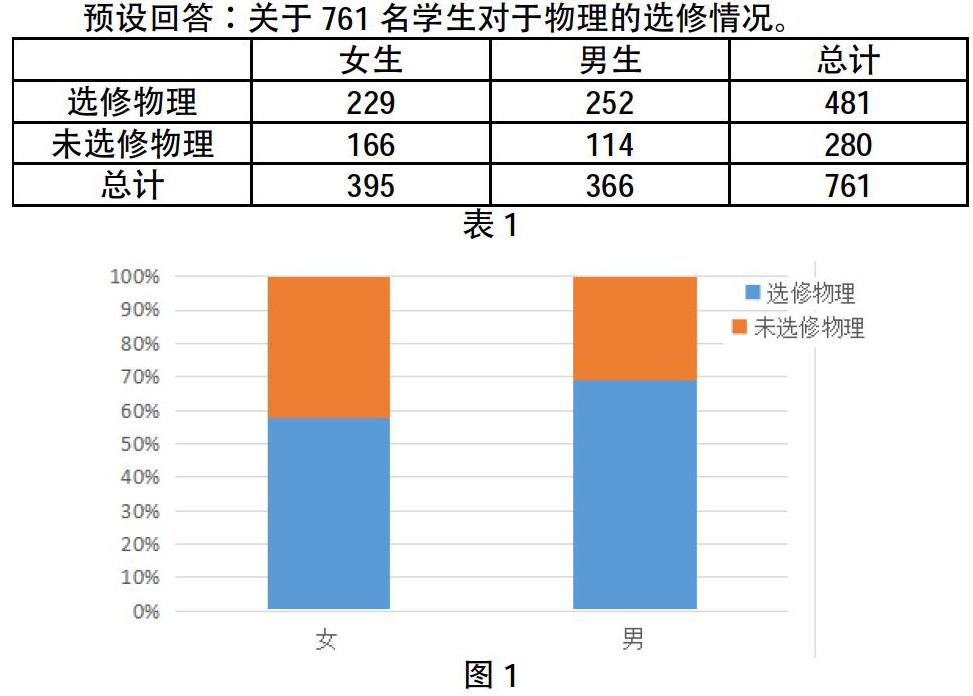
预设回答：关于761名学生对于物理的选修情况。

预设回答：可以计算比例，女生中选修物理的频率是 ，男生中选修物理的频率是 ，男生选修物理的频率大，所以认为有关。

（二）问题驱动

问题1：由以上两种方法，我们初步得到了结论高中生选修物理与性别有关，我们得到的判断是否可靠呢？

设计意图：描述判断两个分类变量有关的可靠性是独立检验的关键，这个问题的设计是为了引出独立性检验的思想。同时让学生体会样本并不能代替总体，但是样本可以估计总体，估计总体也要研究它的可靠性。

问题2：本例中，我们得到的结论犯错误的可能性有多大呢？换句话说，我们能有多大的把握认为高中生选修物理与性别有关呢？

问题3：样本容量的大小对于 的大小有着很大的影响，有没有更合理的方法呢？

设计意图：体会数学中统计量的设计有相通的特点，在这里也体现类比的数学思想，让学生简单理解 公式结构的合理之处。让学生强化：如果假设成立，那么的观测值应该很小。引出此数据的大小应该有一个标准来衡量。

问题4：利用这个公式计算出的数我们称为 的观测值， 观测值的大小应该如何衡量呢？

设计意图：引出的临界值表，让学生全面了解统计学家研究独立性检验的完整经验。同时让学生学会准确地下统计学的结论，同时体会数学的严谨性。任何事物都有两面性，不同的结果可以得到不同的结论，同样也要做出正确的判断。

问题5：独立性检验的原理与数学中的什么方法的原理类似？它们有什么区别？

设计意图：一方面使学生深化对独立性检验基本思想方法的认识;另一方面让学生通过对新、旧知识的对比辨析，建立新知识与已有相关知识的实质性联系，将新知合理纳入原有知识结构。

问题6：你能否总结一下利用独立性检验判断两个分类变量是否有关的基本步骤？

设计意图：让学生对具体问题做出总结，能够将特殊推广到一般，得到判断两个分类变量有关系的方法，理解独立性检验的思想。同时也为了让学生梳理利用统计知识研究问题的整个过程，为了后面更好地解决实际问题作好铺垫。

（三）课堂小结：

1.知识小结：独立性检验的基本思想与独立性检验的基本步骤

2.数学思想方法：（1）类比推理

（2）从一般到特殊，从特殊到一般。

（3）统计学的基本思想：搜集数据，整理数据，分析数据，由数据分析得出结论。

3.核心素养：逻辑推理、数学建模、数学运算、数据分析。

（四）课下作业：

课前老师让各小组都搜集了你们感兴趣的分类变量的相关数据，之前我们只是简单地判断了一下分类变量是否有关，学习本节课后，你能否利用本节课我们所学的独立性检验进行判断，看各自有多大的把握认为它们有关系？

参考文献：

[1]王太军. 基于学生实践能力培养的普通高中物理实验课程建构研究[D].西北师范大学，2016.

[2]秦鑫.新课改背景下的高中物理课堂教学[J].教育教学论坛，2010（33）：165.