奇妙的三阶幻方
2020-11-27 03:23
小学生学习指导(中年级) 2020年11期
【例1】在下图的3×3阵列中填入了1~9的自然数,构成了大家熟悉的三阶幻方。
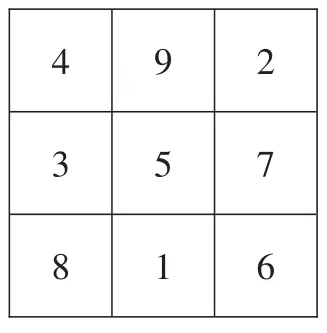
现在另有一个3×3的阵列,请选择九个不同的自然数填入九个方格中,使其中最大者为20,最小者大于5,且每行、每列及每条对角线上的三个数的和都相等。
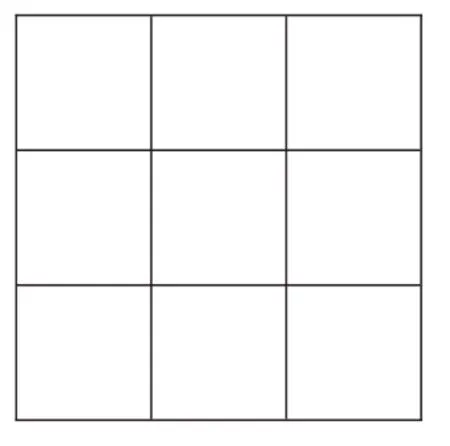
【思路点睛】最基本的三阶幻方中,填入的是1~9 这九个不同的自然数,其中最大的为9,最小的为1。要使新编制的幻方中最大数为20,而9+11=20,因此,如果在所给幻方中各数都增加11,就能构成一个新幻方,并且满足最大数为20,最小数大于5。如下图:

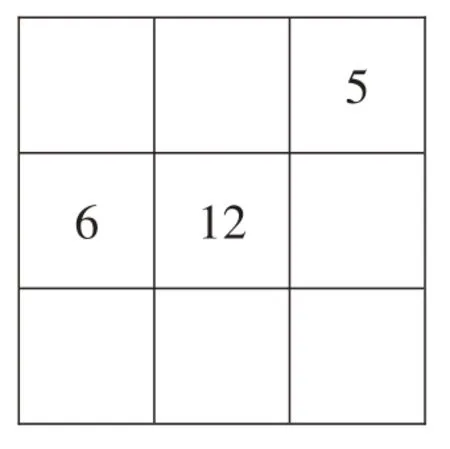
【例2】在3×3 的阵列中,第一行第三列的位置上填5,第二行第一列的位置上填6,如下图。请你在其他方格中填上适当的数,使方阵横、纵、斜三个方向的三个数之和为36。

【思路点睛】因为三个数的和是36,所以可求出三个数的平均数是36÷3=12,这个12也就是中心数,即填在幻方中间的数。
填出了中间数,那么第二行右边的数就是36-12-6=18;对角线左下角的数是36-12-5=19。

得到了这两个数,剩下的就好办了。用36减去已知数,得到剩下的数:
36-19-6=11;36-18-5=13;36-11-5=20;36-19-13=4。

从上面的例题我们不难看出:要填出一个三阶幻方,中心数起着至关重要的作用。利用“三个数的和=中心数×3”这个关系式,在已知和的情况下,可先求出中心数;在得到中心数的情况下,利用三个数的和,求出其他数。
猜你喜欢
知识文库(2017年21期)2017-10-20
新东方英语·中学版(2017年9期)2017-09-25
学生天地·小学低年级版(2017年5期)2017-06-07
环球人物(2017年3期)2017-03-31
中学生数理化·八年级数学人教版(2017年1期)2017-03-25
中学生数理化·七年级数学人教版(2017年2期)2017-03-25
中学生数理化·七年级数学人教版(2016年8期)2016-12-07
中学生数理化·七年级数学人教版(2016年8期)2016-12-07
初中生世界·九年级(2016年4期)2016-04-21
国外科技新书评介(2014年12期)2015-01-05
- 小学生学习指导(中年级)的其它文章
- “平均分”是关键
- 生活中的条形统计图
- 复式条形统计图绘制五部曲
- 走马观花
- “平行四边形和梯形”测试卷
- 怎样搭配

