论构造法在初中数学中的应用

张玉婷

（河北省唐山市乐亭县汤家河镇汤家河初级中学，河北唐山 063600）

在解答数学问题时，我们时常会采用这样一种方法，即通过对已知的条件和所给结论进行分析，构造出辅助的内容，它既可以是一个图形、一个方程(组)、一个等式、一个函数或是一个等价命题等，将所给条件与所给结论结合起来，从而最终将问题解决，而以这种形式来解题的数学方法，我们称它为构造法[1]。

运用构造法解决问题，可以将代数、三角、几何等各种数学知识互相连接在一起，更能使问题得到快速且简便的解决。有部分数学问题从表面上感觉难以解答，但是当我们将已知条件为基本内容加以创造性地运用，把所要求的结论确定为解决题目的方向，高效地运用已有数学知识，构造出相应的辅助性问题及其数学形式，就可以使得问题在崭新的形式下得到简便解法，这也就是在解题中的“构造”方略。

1 构造法的定义

数学中的构造法，就是根据问题所给出的条件和结论传达的信息，把问题作合适的加工处理，高效地运用所知数学知识，构造出与所给问题相关联的数学模式，深入发掘问题的本质，进而使得问题在崭新的形式下得到简便解法。构造法的本质是创造性地运用所知数学知识去解决一些数学问题，它不仅仅是一种解题的方式方法，而且是创造性解题方法的方法。

2 构造法的特点

构造法作为一种常见的数学解题方法，在解决数学问题时具有多种特点：

（1）通过构造辅助性问题对原有问题进行一定的转化，使解题思路更加清晰。

（2）运用构造法解决问题可以使问题更加清晰、直观，解题过程更加顺畅。

（3）运用构造法解决问题，对学生的数学能力是有一定要求的，构造法的变化形式多样，针对不同的问题，会采用不同的构造形式。而面对问题，学生是否能够想到对应的构造方法，这就需要学生具有良好的数学素养和较强的思维能力[2]。

在学生遇到难以解决的数学问题时，不妨认真思考一下是否能够运用构造法解决问题，这既是对学生的一种思维锻炼，也是对他们数学素质的一种培养。如果学生能够很好地运用这种数学方法，学生会有一种“大彻大悟”的感觉，困难的数学问题在解决过程中也会感到得心应手，而不是束手无策。

3 构造法的实际应用

很多的数学问题较为复杂，在学生解题过程中可能不知从何处入手，但当我们能够构造出相应的数学模型，能够巧妙运用构造的方法来进行解题时，我们往往能够实现从量变到质变的飞跃。

3.1 构造法在方程中的应用

构造方程就是用已知条件作基础，用所求结论作为解答方向，构造出一个方程，然后再根据方程的相关内容，就能够使得问题在利用方程的知识下简便快速解决。

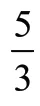
3.2 构造法在几何中的应用

在几何题目中，很多题难以通过直观形式求证得出，而通过对几何图形构造辅助线，构造出恰当的图形，使各部分的关系更加清晰明了，可以使得问题更容易解决，拓宽学生的解题思路，也锻炼了学生的几何思维能力。

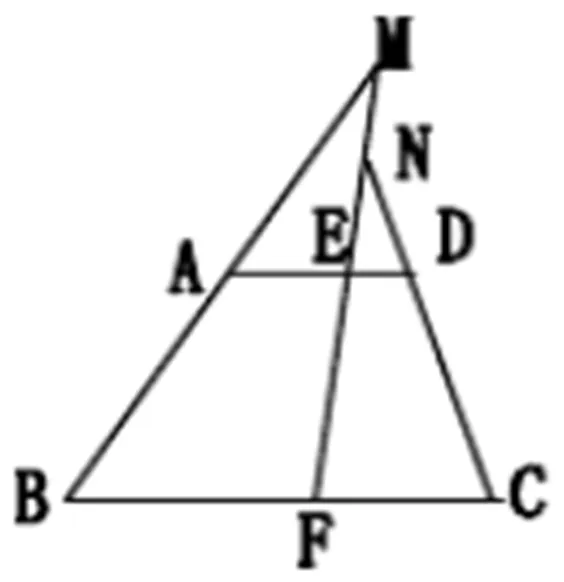
案例：如图所示，在四边形ABCD 中，AB=CD，E、F 分别为AD、BC 的中点，BA、CD 的延长线分别交FE 的延长线于M、N，求证：∠AME=∠DNE。

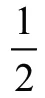
3.3 构造法在绝对值中的应用

在解答绝对值的问题时，我们常采用画数轴的方式来解决此类问题，利用数轴我们可以判断某些代数式的正负以及它们的距离问题。

案例：当a 取何值时，|a+5|+|a-1|+|a-4|的值最小，最小值为多少？请说明理由。

解析：线段上的点与两端点的距离和最小，判断出a=1 时，三个绝对值的和最小，所以当a=1 有最小值，最小值=|1+5|+|1-1|+|1-4|=6+0+3=9。

理由：线段上的点到线段两端点的距离的和最小，a=1 时，正好是3 与-4 两点间的距离。故答案为：当a=1 有最小值，最小值为9。

3.4 构造法在不等式的应用

不等式是初中数学的一个重要组成部分，既是初中数学学习的难点也是重点，对于高中的数列学习也具有一定的帮助，且不等式历来是中考热门话题，而通过构造法不等式可以在不需要得出确定值的情况下将问题解决，我们只需依靠不等式确定所求解区间即可，大大减少了运算过程，增加了准确率。

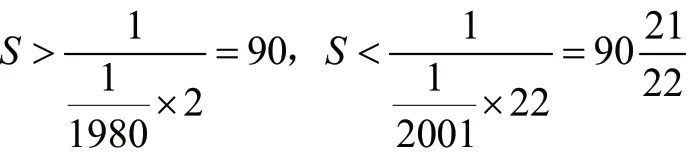
综上所述，S 的整数部分是90。

综上所述，构造法在初中数学中的应用较为广泛，构造法可应用的题型是多样的，通过运用构造法，使得方程问题、几何问题、不等式问题、绝对值问题等都能化难为简，拓宽学生的解题思路，帮助学生进行思维发散。在初中阶段，如果学生能够熟练掌握这种数学解题方法，那么能极大提高学生的问题解答效率，同时也提高了准确率[3]。学生运用构造法进行解答问题的过程，也是学生对数学知识的迁移过程，在运用构造法解题时，学生会发现题目所运用的知识点是有所关联的，由此，长时间熟练运用这种方法，学生能够对所学知识形成一个完整的知识体系，同时能够养成良好的数学学习习惯。初中数学与高中数学是有一定的关联性的，在初中阶段打下良好的数学学习基础，对于高中数学的学习是有极大的帮助的，同时在初中阶段做好学生的逻辑思维训练，帮助学生发展思维能力并且使学生掌握一定的解题技巧，提升学生的数学素质也是尤为重要的。