近断层速度脉冲向前方向性效应和滑冲效应对巨-子结构体系地震反应的影响

王 瑶， 谭 平*， 李祥秀， 杨 奎

(1.广州大学 工程抗震研究中心， 广东 广州 510405； 2.中国地震局地球物理研究所， 北京 100081)

从二十世纪五十年代起，近场地震由于其对结构产生的强大破坏力而引起地震工程界的关注.近年来，近断层速度脉冲型地震动在其产生机理上取得了重要的研究成果.一些学者们分别从能量叠加[1]、脉冲与相位差[2]、震源[3]等角度探讨了速度脉冲的产生机理，这些研究表明：地震断层的破裂速度与横波的传播速度相同或接近时，会引起波形叠加从而产生速度脉冲效应.刘启方等[4]提出将速度脉冲型地震动分为由破裂传播的多普勒效应引起的地震动向前方向性速度脉冲和由断层的滑冲效应引起的地震动滑冲效应速度脉冲两类.向前方向性效应速度脉冲主要发生于垂直于断层面的方向，而滑冲效应速度脉冲发生在断层的滑动方向[5]；滑冲效应一般使地震动速度时程中出现单向脉冲，而向前方向效应一般表现为双向或者多向速度脉冲[6].因此，这两种产生机制的速度脉冲效应也可能会对不同形式的结构产生不同的破坏效果.

巨-子结构控制体系，即在巨型框架结构的基础上将子结构顶部与主结构底部的连接断开，放松主结构和子结构的侧向连接，使主、子结构之间产生相对运动从而形成的一种新型结构体系[7]，其整体性好、抗侧能力强，适用于高层或超高层建筑，是未来发展的一个重要方向.近年来，随着近断层地震动记录的增加以及高层或超高层建筑需求的增多，一些学者开始将目光投向了近断层地震动对巨-子结构体系的动力性能影响.颜学渊等[8]通过振动台试验对比分析了巨-子结构抗震体系和隔震体系在近场和远场地震动作用下的地震反应，结果表明主结构和子结构在近场地震作用下的位移反应均大于相同场地的远场地震作用；李祥秀等[9]以抗震、隔震及智能隔震这三种不同控制策略的巨-子结构体系为对象，采用数值分析分别计算了这三种体系在近断层速度脉冲地震动作用下的地震响应，结果表明速度脉冲效应对三种结构体系在地震下的响应均有不利的影响，其中采用SMA-压电阻尼器的智能隔震体系最为敏感.以上研究成果均表明近断层地震动会对巨-子结构体系产生更加不利的影响.然而，两种不同产生机制的近断层速度脉冲型地震动对巨-子结构体系的位移反应有何影响差异、差异有多大以及会对结构产生何种破坏效果还未进行过全面详细的量化分析.

本文以巨-子结构抗震体系和隔震体系为研究对象，在基于加速度反应谱一致的情况下，选取具有向前方向性和滑冲效应两种不同速度脉冲特性的实际地震动和人工合成不含速度脉冲的地震动作为输入，采用大型有限元软件SAP2000开展结构地震反应计算，定量地分析近断层速度脉冲地震动作用下巨-子结构体系的地震响应，探究两组不同产生机制的速度脉冲地震动对巨-子结构体系的影响差异.

1 巨-子结构分析模型和运动方程

1.1 分析模型

巨-子抗震结构的各层主结构和子结构之间为固接，巨-子隔震结构的各层主结构和子结构底部通过设置隔震装置连接.其简化模型如图1所示.

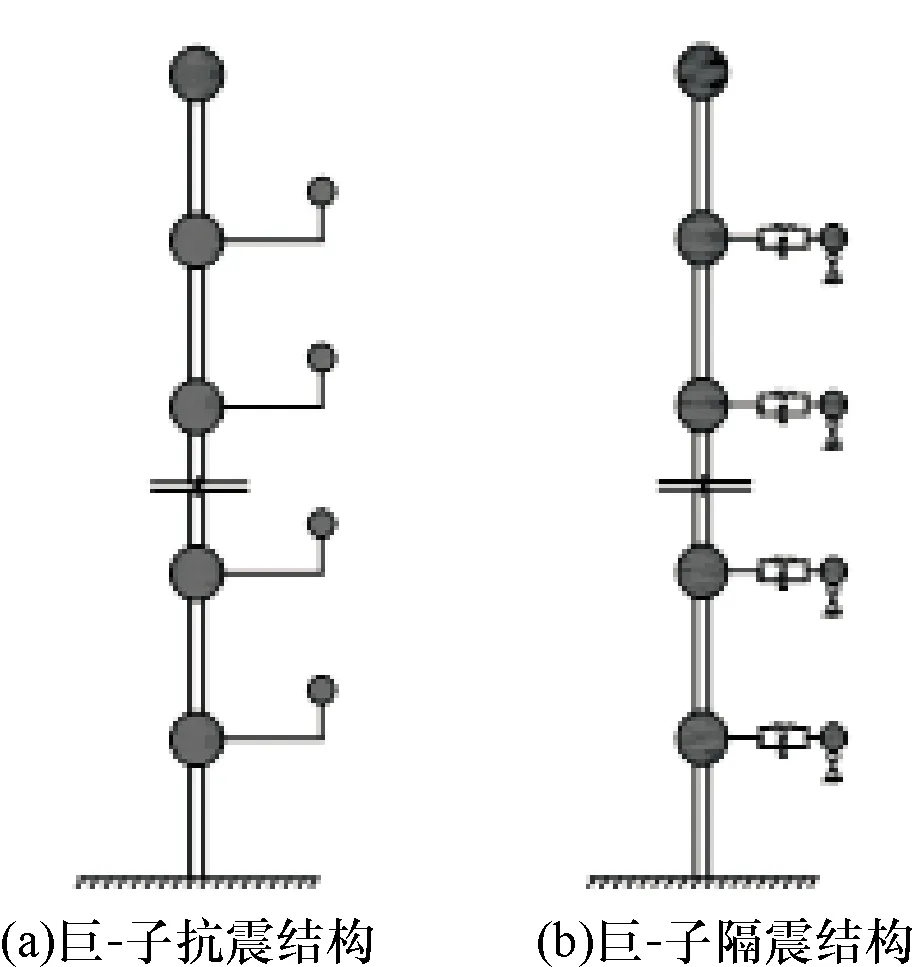
图1 分析模型Fig.1 Analysis model

1.2 运动方程

根据D’Alembert原理，建立巨-子隔震结构体系的运动方程如下：

(1)对于子结构：

(1)

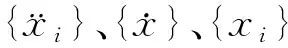
(2)对于主结构:

(2)

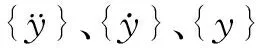
联立方程(1)与方程(2)，可得结构的整体运动方程：

(3)

其中,{z}=[{x}T{y}T]T、{x}、{y}分别为子结构与主结构与地面的相对位移，巨-子结构体系的整体质量矩阵、刚度矩阵、阻尼矩阵如下方式组装：

(4)

其中，

[mi]=diag[m1,m2,…,mi]

(5)

[ki]=diag[k1,k2,…,ki]

(6)

[ci]=diag[c1,c2,…,ci]

(7)

ki与ci为隔震装置的刚度与阻尼.

巨-子隔震结构的运动方程即可用上述方法求得，而巨-子抗震结构则按子结构单元与主结构相固结求得.

2 地震动的选取

目前，近断层地震动速度脉冲还没有一个严谨的定义，因此对这种脉冲型地震动的识别也还没有一个统一的标准[10].一般来说，速度脉冲型地震动具有急剧突起的波形、特征周期延长、中长周期分量丰富，且地面速度峰值与地面加速度峰值的比值(PGV/PGA)较大.本文参考韦韬[11]提出的判别标准来选取输入的速度脉冲地震动：①速度脉冲持续时间在0.5 s以上；②速度时程中最大峰值是第二大峰值的二倍以上，若有两个峰值比较接近，则峰值较小者是其余最大峰值的两倍以上.此外，近断层速度脉冲地震波根据其产生机理可以分为向前方向性效应和滑冲效应两类，这两种效应会导致近断层地震动产生两种不同的长周期速度脉冲，使结构在地震初始就被输入很高的能量，从而引起强烈的结构破坏.向前方向性效应在时程上主要表现为大幅值、脉冲波形明显、持时短，多呈现为一个双向速度脉冲；滑冲效应主要表现在与断层滑动方向平行的分量上，多呈现为一个单向脉冲.

按照上述判别标准并结合巨-子结构体系的基本特性，选取了不同产生机理的天然速度脉冲型地震动，包括向前方向性效应和滑冲效应各两条对上文的两种结构体系进行结构动力分析.由于地震动反应谱特性的差异会引起结构地震响应的差异，因此在对比有无速度脉冲地震动对结构响应造成的影响差异时，应该尽可能排除反应谱差异对其的影响，使两组地震动的加速度反应谱差异控制在某个值以内.贺秋梅等[12]提出了一种以地震动加速度反应谱和峰值加速度为目标，同时控制峰值速度和位移的人工合成地震动的方法.这种方法合成的地震动与实际地震动具有相同的加速度峰值、弹性反应谱和持时，但是不再具备速度脉冲特性.本文采用该方法分别对每一条实际地震动进行拟合，表1为所选地震动记录的相关参数以及对应的人工合成地震动的代号，图2和图3为天然速度脉冲地震动和人工合成地震动加速度和速度时程的部分样本.在进行动力时程分析时，将峰值加速度调整至7度(0.15 g)罕遇地震所对应的值.

表1 近断层速度脉冲型地震动记录参数Table 1 Recording parameters of near-fault velocity pulsed ground motion

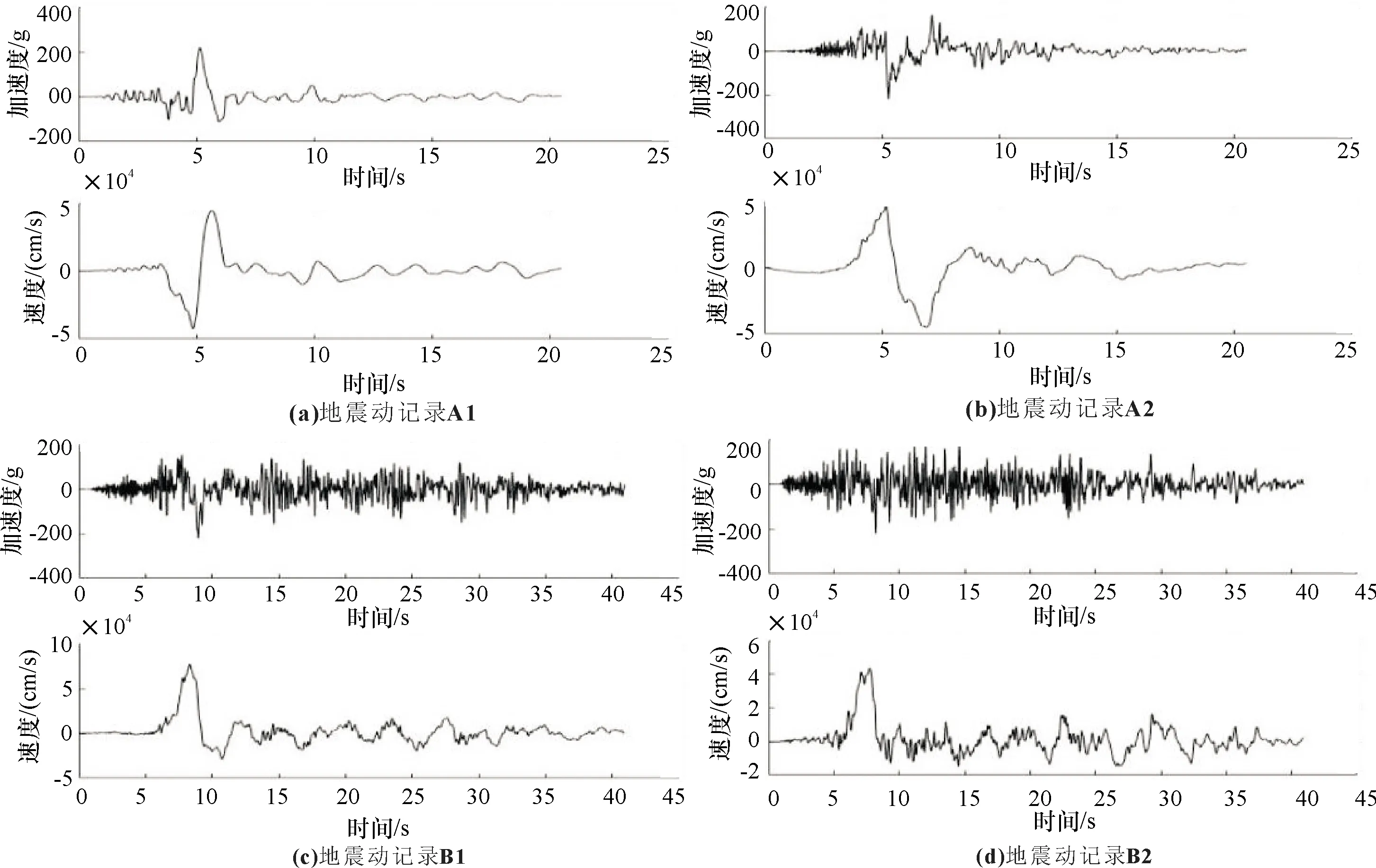
图2 速度脉冲地震动记录的加速度和速度时程Fig.2 Acceleration and velocity time history of velocity pulsed ground motion

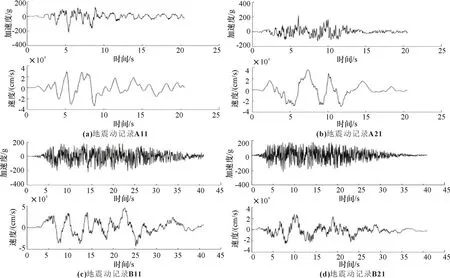
图3 部分人工合成地震动记录的加速度和速度时程Fig.3 Part of acceleration and velocity time history of artificial ground motion

3 脉冲影响系数

为了衡量两种不同产生机制的速度脉冲地震动对巨-子结构体系位移反应的影响结果，引入方向性脉冲影响系数α和滑冲脉冲影响系数β，分别定义为

(8)

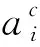
4 算例分析

采用有限元分析软件SAP2000建立钢框架巨-子抗震结构和隔震结构.其主结构为三层，每层主结构上设置七层子结构，结构所用钢材均为Q235，采用弹性的本构关系.两个模型的三维图相同，如图4所示.

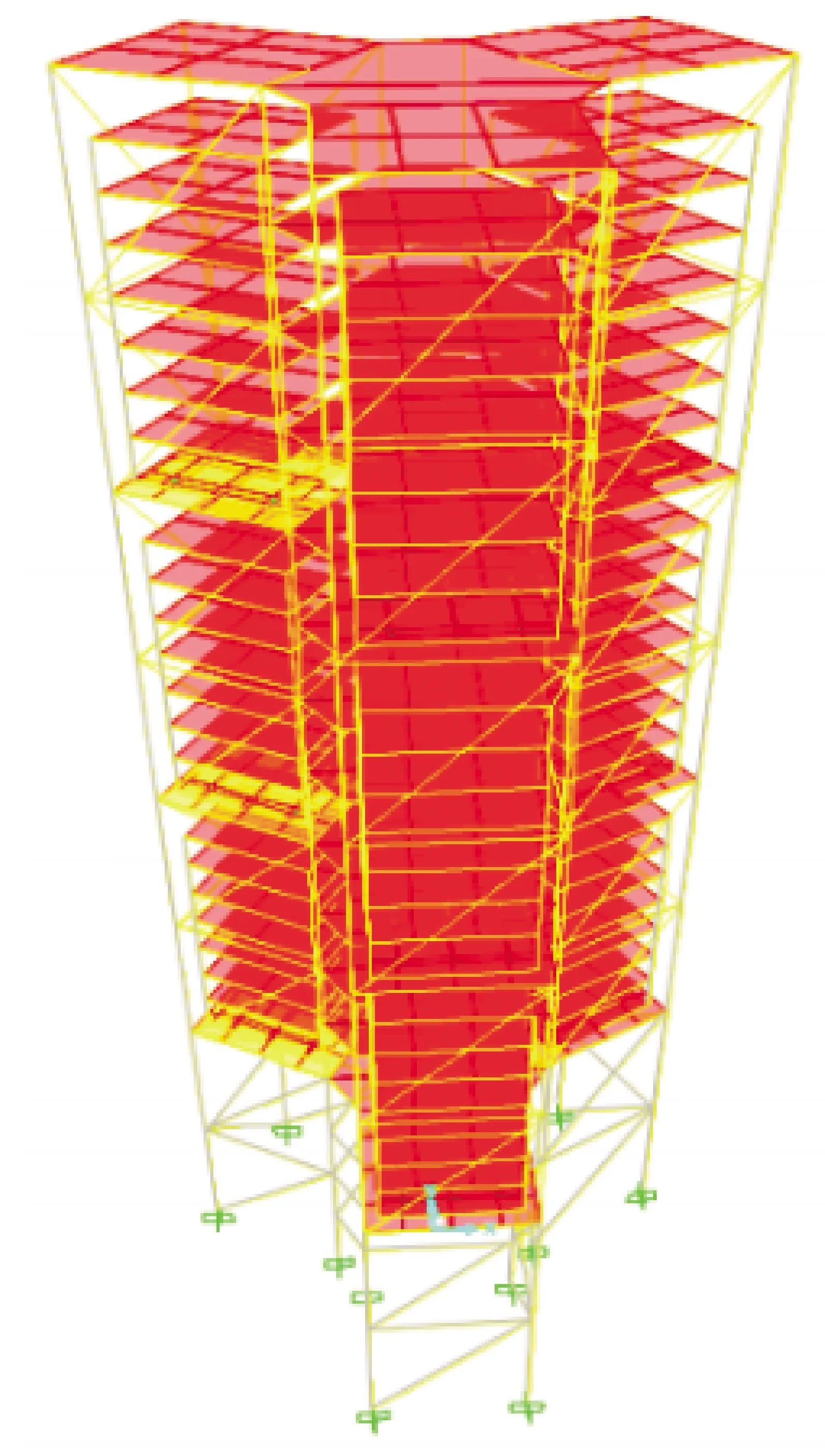
图4 有限元分析模型三维图Fig.4 3D diagram of finite element analysis model

图4中，抗震结构中子结构与主结构底部固结，隔震结构中子结构与主结构采用Rubber Isolator和Damper连接单元连接，阻尼取值为1.417，阻尼指数为0.275.

对结构进行模态分析，得到巨-子抗震结构和隔震结构前3阶模态的自振周期如表2所示.可以看到子结构加入隔震装置隔震后较抗震结构的自振周期有所延长.

表2 模型周期Table 2 Period of the model

4.1 主结构层间位移响应

图5给出了X向巨-子抗震结构和巨-子隔震结构在向前方向性效应和滑冲效应速度脉冲地震动下主结构各层最大位移和脉冲影响系数.由于结构对称，扭转作用影响较小，且隔震装置各向同性，结构力学性能双向对称，Y向的计算结果与X向结果相似，因此不再一一展示.

由图5可知，巨-子抗震结构在两组向前方向性效应速度脉冲地震动下的脉冲影响系数均值为1.04，在两组滑冲效应速度脉冲地震动下的脉冲影响系数均值为1.01.巨-子隔震结构在两组向前方向性速度脉冲地震动下的脉冲影响系数均值为1.43，在两组滑冲速度脉冲地震动下的脉冲影响系数均值为1.47.因此，两类速度脉冲地震动对巨-子抗震结构主结构各层位移影响较小，方向性脉冲影响系数略大于滑冲脉冲影响系数，略大3%；而巨-子隔震结构的主结构各层位移在两类速度脉冲天然地震动作用下相比于无速度脉冲人工地震动作用下分别增大了1.43倍和1.47倍，滑冲效应速度脉冲影响系数略大于向前方向性效应速度脉冲影响系数，略增大3%.

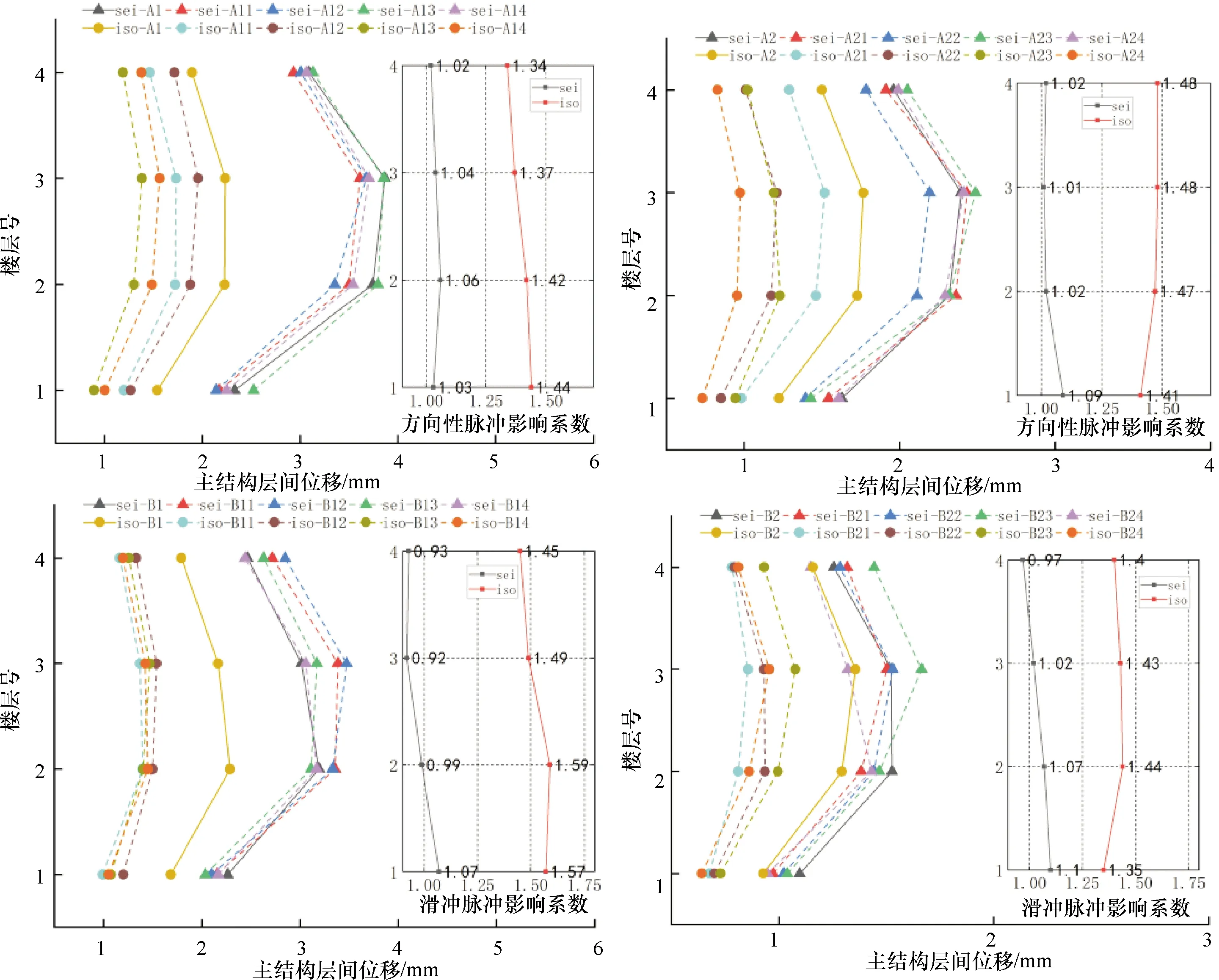
图5 速度脉冲地震动作用下的主结构各层位移和脉冲影响系数Fig.5 Displacement and pulse influence coefficient of each layer of the megastructure under the action of velocity pulse ground motion

4.2 子结构层间位移响应

图6给出了X向巨-子抗震结构和巨-子隔震结构在向前方向性效应和滑冲效应速度脉冲地震动下子结构各层最大位移和脉冲影响系数.由图6可知巨-子抗震结构的方向性脉冲影响系数均值为1.07，滑冲脉冲影响系数均值为1.02；巨-子隔震结构方向性脉冲影响系数均值和滑冲脉冲影响系数均值都为1.44.因此，两类速度脉冲地震动对巨-子抗震结构子结构各层位移影响较小，方向性脉冲影响系数略大于滑冲脉冲影响系数，略增大5%；而巨-子隔震结构的主结构各层位移在两类速度脉冲天然地震动作用下相比于无速度脉冲人工地震动作用下均增大了1.44倍，方向性脉冲影响系数均值与滑冲脉冲影响系数相等，即两类速度脉冲地震动对子结构位移的影响相当.

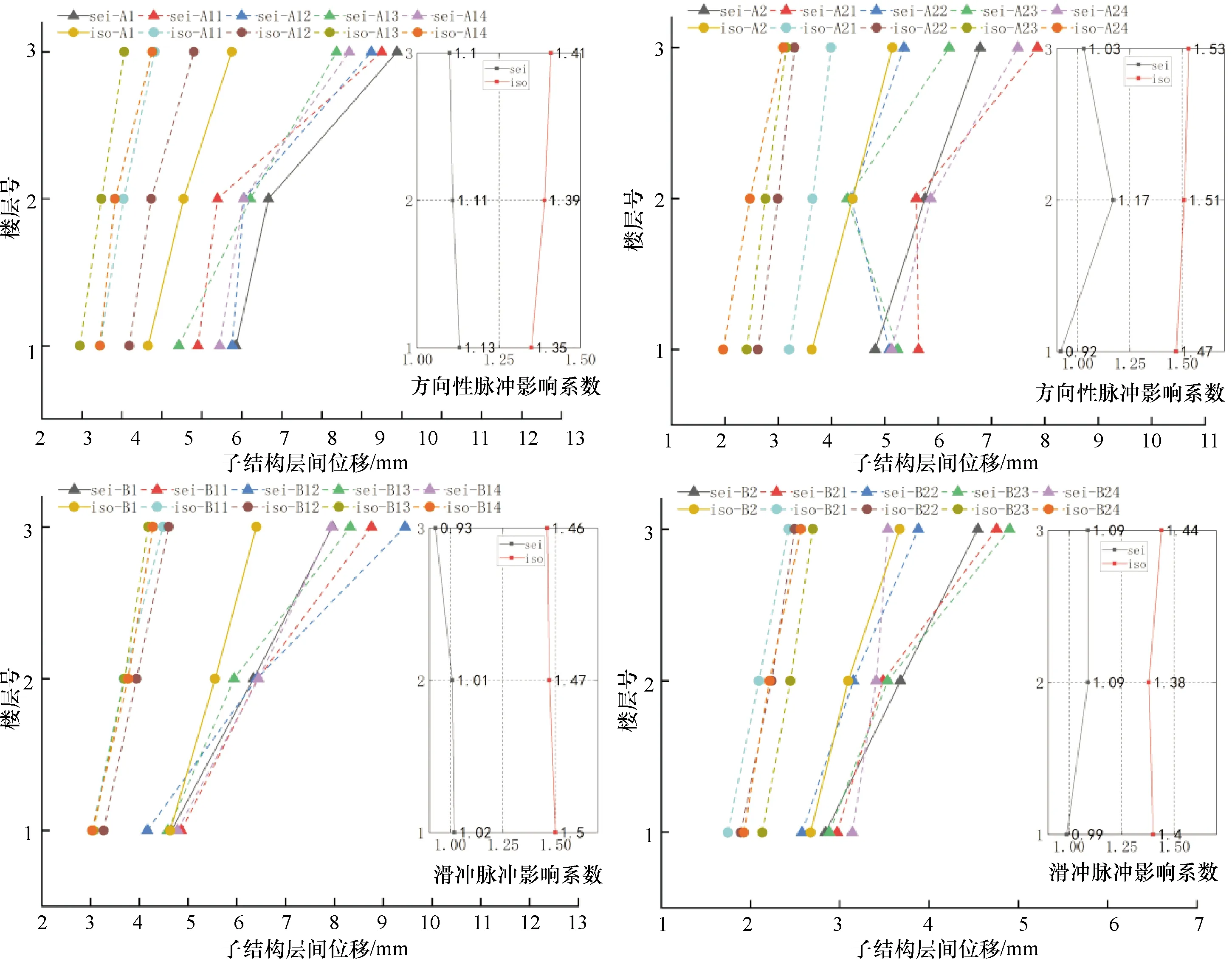
图6 速度脉冲地震动作用下的子结构各层位移和脉冲影响系数Fig.6 Displacement and pulse influence coefficient of each layer of the substructure under the action of velocity pulse ground motion

4.3 隔震层位移响应

表3给出了X向巨-子隔震结构在向前方向性效应和滑冲效应速度脉冲地震动下隔震层最大位移和脉冲影响系数.由此可知，方向性脉冲影响系数均值为1.44，滑冲脉冲影响系数为1.41，因此向前方向性效应比滑冲效应对隔震层位移的影响更大，增大2.1%.

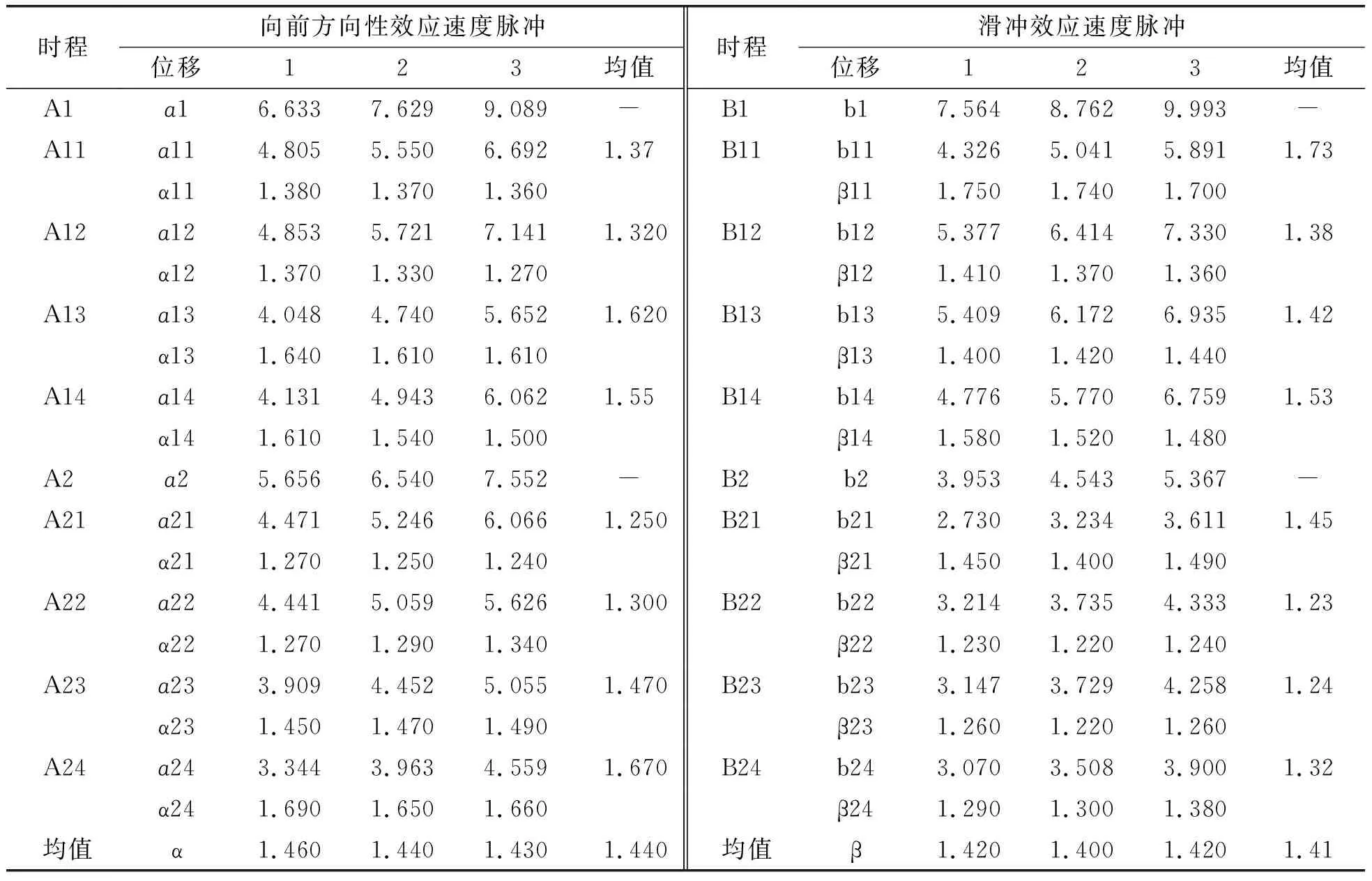
表3 巨-子隔震结构隔震层最大位移和脉冲影响系数Table 3 Maximum displacement and pulse influence coefficient of the isolation layer of the mega-sub isolation structure

4.4 归一化脉冲影响系数

为了更直观地展现两类速度脉冲地震动对巨-子结构体系各层变形的影响程度，对结构各层的位移脉冲影响系数进行归一化，并绘制曲线如图7～图11所示.其中归一化系数=各层位移脉冲影响系数/最小位移脉冲影响系数.

巨-子抗震结构主结构和子结构各层的归一化脉冲影响系数分别如图7和图8所示.由图可知，向前方向性效应和滑冲效应均对主结构的底部变形影响最大，对主结构的顶部变形影响最小；且均对中部子结构影响最大，对底部子结构影响最小.

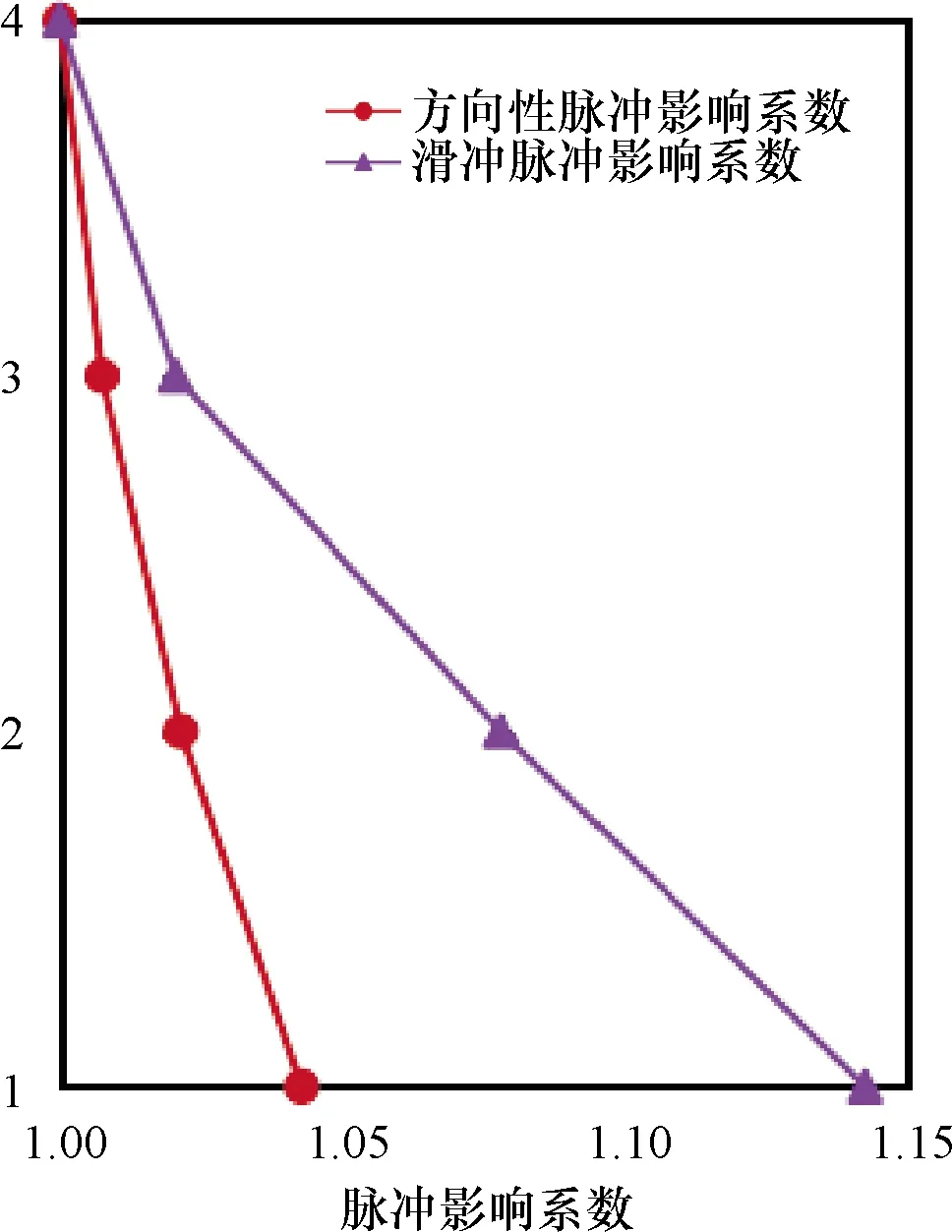
图7 巨-子抗震结构主结构各层脉冲影响系数Fig.7 Pulse influence coefficient of each layer of the megastructure of mega-sub seismic structure

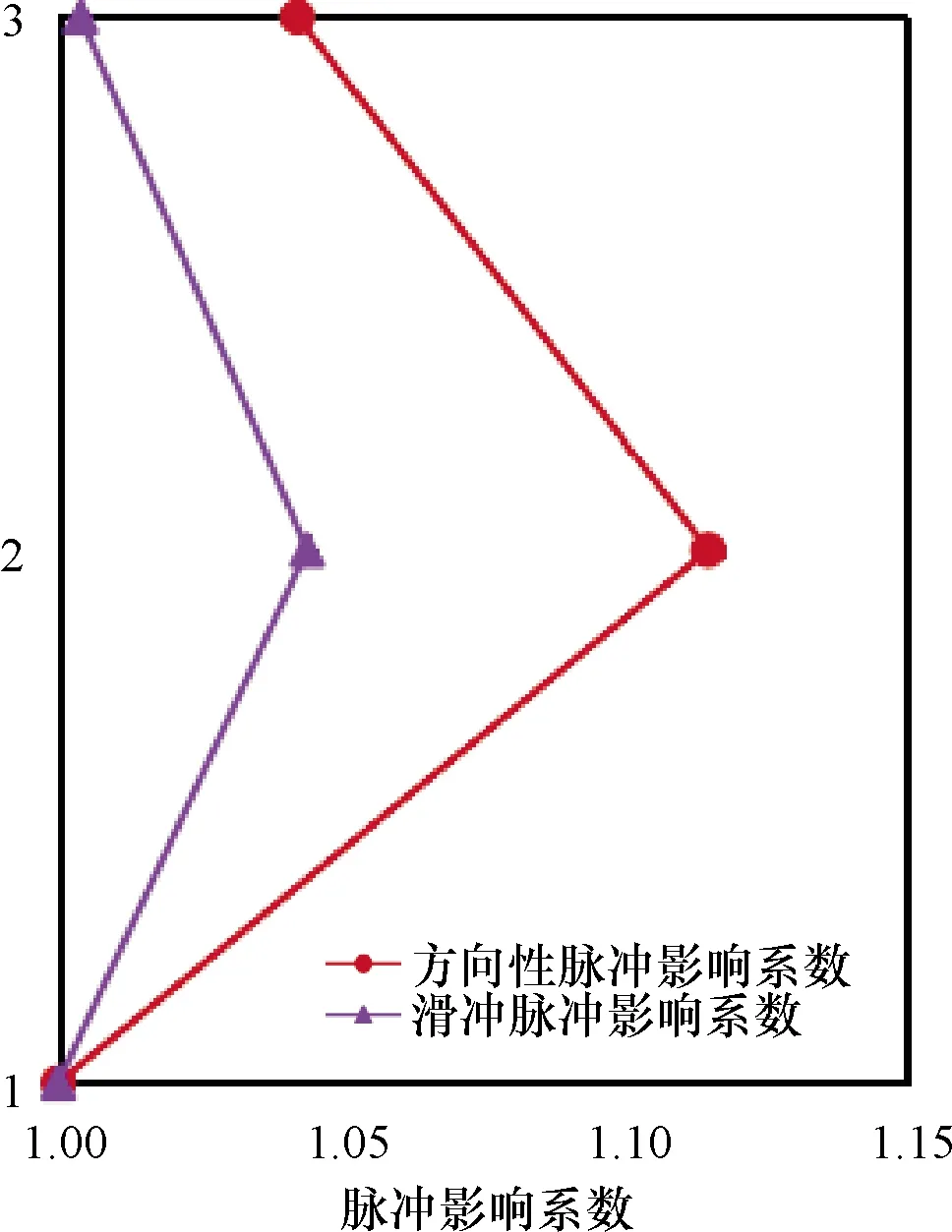
图8 巨-子抗震结构子结构各层脉冲影响系数Fig.8 Pulse influence coefficient of each layer of the substructure of mega-sub seismic structure

巨-子隔震结构主结构和子结构各层的归一化脉冲影响系数分别如图9和图10所示.由图可知，向前方向性效应和滑冲效应均对主结构中间层的变形影响最大，对主结构顶部变形影响最小；且均对顶部子结构变形影响最大.图11为巨-子隔震结构隔震层归一化脉冲影响系数.由图可知，向前方向性效应速度脉冲对结构底部隔震层位移影响最大，滑冲效应速度脉冲对结构底部和顶部隔震层位移影响都很大.

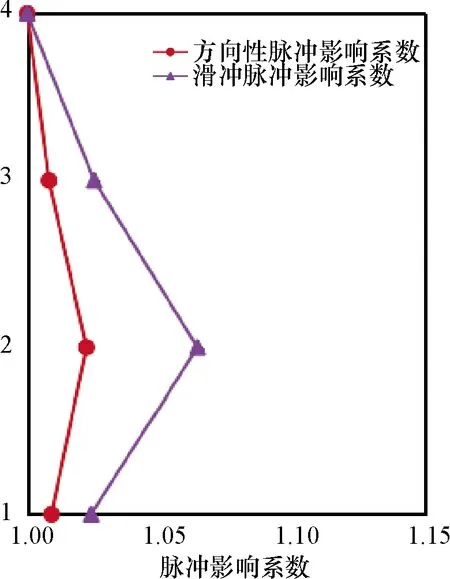
图9 巨-子隔震结构主结构各层脉冲影响系数Fig.9 Pulse influence coefficient of each layer of the megastructure of mega-sub isolation structure

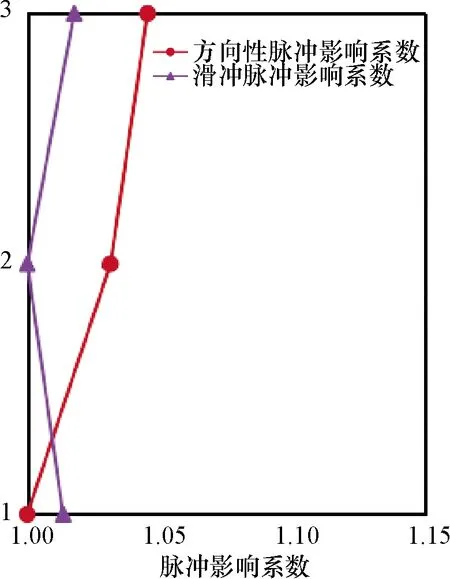
图10 巨-子隔震结构子结构各层脉冲影响系数Fig.10 Pulse influence coefficient of each layer of the substructure of mega-sub isolation structure

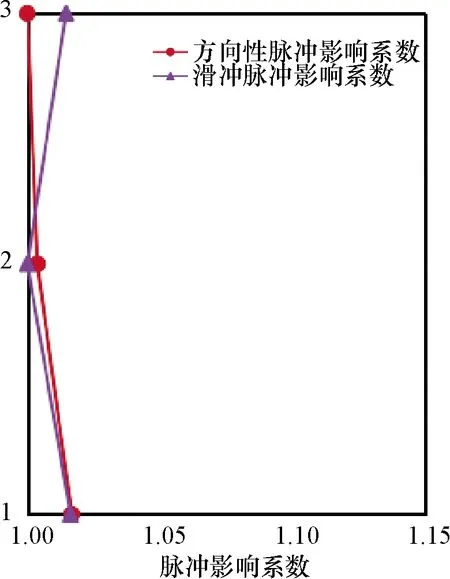
图11 巨-子隔震结构隔震层位移脉冲影响系数Fig.11 Pulse influence coefficient of the isolation layer of the mega-sub isolation structure

5 结 论

本文以巨-子结构抗震体系和隔震体系为研究对象，定量地分析了两组不同产生机制的速度脉冲地震动对巨-子结构体系的影响差异.在本文所选用的地震动记录作用下，得到以下结论：

(1)向前方向性效应速度脉冲地震动使巨-子抗震结构的主结构位移反应和子结构位移反应分别增大了1.04倍、1.07倍；滑冲效应速度脉冲地震动使巨-子抗震结构的主结构位移反应和子结构位移反应分别增大了1.01倍、1.02倍.向前方向性效应速度脉冲地震动使巨-子隔震结构的主结构位移反应、子结构位移反应和隔震层位移反应分别增大了1.43倍、1.44倍和1.44倍；滑冲效应速度脉冲地震动使巨-子隔震结构的主结构位移反应、子结构位移反应和隔震层位移反应分别增大了1.47倍、1.44倍和1.41倍.因此，相比于巨-子抗震结构，在近断层区域内的巨-子隔震结构更应该考虑速度脉冲对结构的影响，防止结构出现大变形而影响其正常使用.

(2)向前方向性效应速度脉冲对巨-子抗震结构在主结构和子结构位移反应的影响上均大于滑冲效应速度脉冲，分别增大3%和5%；而对于巨-子隔震结构，向前方向性效应对隔震层位移的影响更大，增大2.1%，滑冲效应对主结构位移的影响更大，增大3%.可见，不同产生机制的速度脉冲对巨-子结构体系不同部位的位移反应影响存在差异，应分别考虑设计重点.

(3)在巨-子抗震结构中，两类速度脉冲地震动均对主结构底部变形的影响大于上部结构，对子结构中上部的影响大于底部；而在巨-子隔震结构中，两类速度脉冲地震动均对主结构中间层和子结构顶层的影响最大，向前方向性效应速度脉冲更容易影响巨-子隔震结构底部隔震层位移，滑冲效应速度脉冲对结构顶部隔震层位移影响最大.