试飞阶段军用飞机任务可靠性增长建模及评估

高雅娟,马涛,武红姣

(中国飞行试验研究院，陕西 西安 710089)

0 引言

可靠性是衡量飞机持续作战能力的重要特性，对其进行科学、经济、有效的评估与验证具有重要意义。而军用飞机的任务可靠性作为型号设计定型/鉴定试飞重要的评估验证内容之一，对于装备作战适用性及作战效能评估具有重要影响[1-2]。文献[3-4]从工程应用的角度提出结合测试性验证以及基于相似产品信息的任务可靠性评估方法。文献[5]提出了基于飞行剖面的军用飞机任务可靠性评估方法。文献[6-7]考虑了环境、应力等因素对可靠性的影响，分别提出飞行参数折合系数法和基于比例风险模型的环境折合系数法。

根据文献[8-9]，如果在设计定型试飞中安排专门的任务剖面进行试飞，则按照点估计进行评估;若定型试飞中未安排专门的任务剖面进行试飞，只是结合其他任务剖面进行评估时，则按照区间估计进行评估计算。由于目前，在型号设计定型/鉴定试飞中，一般不安排专项任务可靠性试飞剖面，只是结合性能试飞同步进行，一般采用文献[10]中的点估计方法计算。

在军用飞机及航空装备设计定型/鉴定试飞期间，存在部分航空装备早期故障并未完全排除，而是在试飞过程中“边试验、边设计更改”，使得航空装备的可靠性呈增长趋势。文献[11]提出复杂系统的寿命并不总是基于指数分布的，应该基于数据检验来确定其分布形式。如果不考虑可靠性增长的因素，则其评估结果无法反映试飞结束时任务可靠性的真实水平。

本文考虑设计定型/鉴定试飞期间军用飞机可靠性增长的现象，分析研究广义Gamma分布曲线特点及其与试飞阶段军用飞机可靠性增长现象的符合性的前提下，提出基于Gamma分布的军用飞机任务可靠性评估模型，并以某型飞机的试飞数据为例，给出该方法的应用示例。

1 可靠性增长理论模型

文献[12]中介绍了几种常用的可靠性增长模型，主要包括AMSAA模型，Duane模型以及Weibull分布等。在具体的工程应用中，AMSAA模型由于约束条件太多且对数据的规律性要求较高，限制其在工程中的应用;而Duane模型则无法给出可靠性的区间估计结果;在Weibull分布中,由于其形状参数的变化，对于故障率递增、递减及不变的情况都有较好的适应性。但是Weibull分布参数的极大似然估计变化呈现不规范性，即使在位置参数为0，且在形状参数大于1时，Weibull分布的故障率从0递增到无穷大，这与工程实际表现出了不相符性。

而Gamma分布故障率曲线较特殊，类似于Weibull分布，且其故障率曲线单调性只与形状参数有关，且不论是单调递增或是递减，Gamma分布的故障率始终有界。文献[13-14]对几种Gamma分布及其与指数分布、威布尔分布进行了对比。Gamma分布的密度函数为

(1)

式中：k为形状参数；θ为尺度参数，取θ=1。

利用E.Glaser准则，其失效率函数为

(2)

当k>1，λ(t)单调递增，失效率增加，可靠性处于下降过程；当k=1，λ(t)为定值，Gamma分布退化为指数分布，失效率为常数即可靠性不变；当k<1，λ(t)单调递减，失效率减小，可靠性处于增长过程。

由图1可以看出，与Weibull分布不同，Gamma分布的故障率是有界的，且当k<1时，和浴盆曲线的早期故障阶段到偶然故障阶段的过渡相似。因此，Gamma分布可以很好地描绘可靠性增长的过程中，故障率逐渐降低，最后趋于稳定值的过程。正是由于Gamma分布的这种特性，文献[15-16]提出将广义Gamma分布用于可靠性评估。

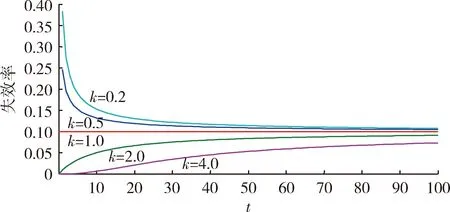
图1 Gamma分布失效率Fig.1 Failure rate of Gamma distribution

2 基于Gamma分布的任务可靠性增长评估模型

鉴于Gamma分布的特点，可利用其将变母体的可靠性增长数据有效地利用起来，评估最终飞机装备的任务可靠度,文献[17-18]给出了Gamma分布参数的估计方法。由于传统的Gamma分布参数的极大似然估计很难求解，本文引入广义Gamma分布，其概率密度函数为

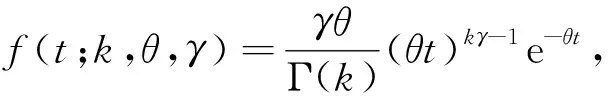
(3)

式中:γ为位置参数。显然，当γ=1时，广义Gamma分布和Gamma分布相同。其似然方程组为

(4)

解上面的方程组即可得到Gamma分布的极大似然估计为

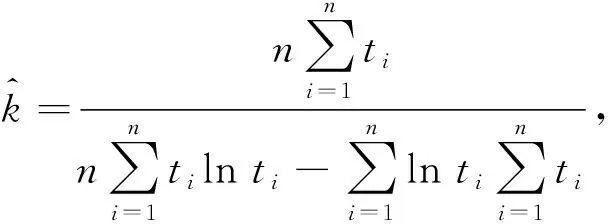
(5)

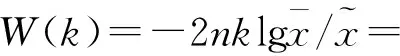
(6)

(7)

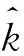
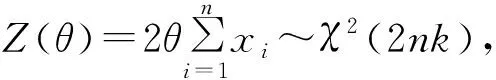
3 基于Gamma分布的某型军用飞机任务可靠性评估

3.1 数据预处理

基于Gamma分布模型的任务可靠性增长评估结果的准确性，主要受到任务成功判据的合理性以及数据收集的准确性的影响。在任务可靠性评估时，故障收集的对象为“会导致飞机任务失败的故障”，主要包括：

(1) 导致飞机延误或取消飞行；

(2) 提前返航或提前着陆；

(3) 任务中断或被迫改变飞行任务；

(4) 导致任务失败或等级事故。

下述情况不计入影响飞机任务可靠性的故障统计次数：

(1) 在执行任务过程中，有余度的系统或设备中的单台发生故障，或与执行本次任务不直接相关的设备或系统发生故障；

(2) 非设备故障所致的任务降级或任务失败。

依据以上任务可靠性评估数据收集及评判原则，对某型军用飞机设计定型试飞期间的数据进行统计。在该评估周期内，某型军用飞机共发生3次故障，分别为200X年X月X1日的2起故障和200X年X月X2日的1起故障。将200X年X月X1日的2个故障拆开，取当天任务时间为这2个相邻故障的间隔时间；第3个故障后的几次试飞未发生故障，则该段时间取为截尾时间；得到故障间隔时间数据如表1所示。

表1 故障间隔时间Table 1 Time Between Failure h

由于观测到的故障较少，且包含1个截尾数据，因此区间估计不采用极大似然估计，而采用填充数据的方法，设最后一个故障间隔时间为以参数估计值为真值的条件分布的期望。

设Z=(z1,z2,…zn-r)为未观测到的失效时间，T=(t1,t2,…tr)为所有观测到失效时间。ρ=(k,θ)，ρ(i)=(k(i),θ(i))为第i次迭代结果。Z服从条件分布，Z～P(Z≤z|Z>tr)。

首先求期望：

(8)

L(T,Z|ρ)=lgp(T,Z|ρ)为完全数据情况下的对数似然函数。给定第i次迭代后的参数估计值ρ(i)，则对Z取条件期望，得到结果：

Q(i)=n(klgθ-lg Γ(k))+

(n-r)(k-1)EZ(lgZ|ρ(i),T)-

(n-r)EZ(Z|ρ(i),T).

(9)

EZ(lgZ|ρ(i),T)和EZ(Z|ρ(i),T)均为无穷积分，且较难计算，因此可采用Monte Carlo模拟得到二者的近似值。

对期望最大化：

(10)

得到

(11)

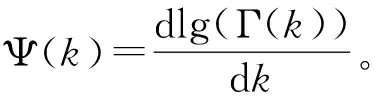
不断重复以上过程，直至最终满足|k(i+1)-k(i)|<ε或|θ(i+1)-θ(i)|<ε，ε为绝对误差限。但是考虑到求期望过程中采用的模拟近似存在一定的波动性，可以对连续多个k(i)值取平均，隔几次迭代后，再对多个k(i)值取平均，比较2次均值的差是否在误差限ε内。为减少收敛时间并考虑模拟期望的波动性，ε可选取稍大一点的值，如取ε=0.05。

3.2 计算过程

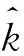
(12)

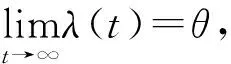
3.3 计算结果

根据以上计算方法，可得某型军用飞机基于Gamma分布的任务可靠性评估结果，且该结果可反映本阶段试飞结束时，该型军用飞机任务可靠性增长后达到的水平。表2给出了某型军用飞机对应不同置信度的任务可靠度下限评估结果。

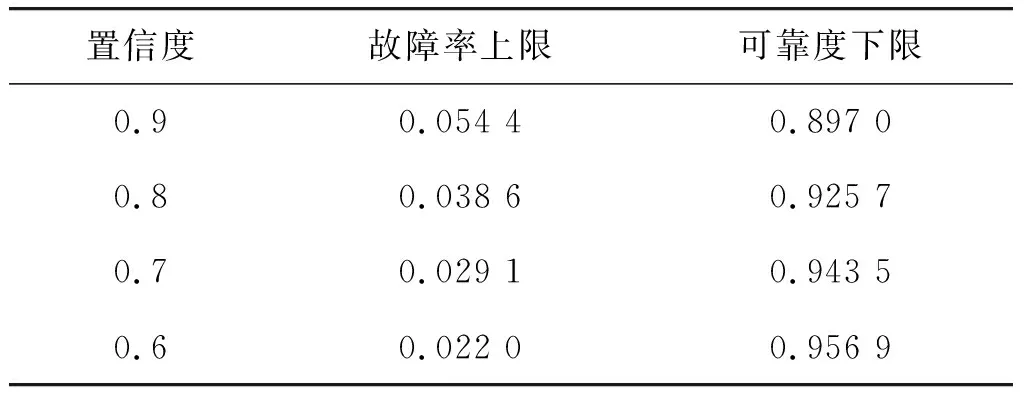
表2 Gamma分布方法的故障率上限和可靠度下限Table 2 Upper limit of failure rate & lower limit of reliability based on gamma distribution

4 结束语

本文通过对几种常用的可靠性增长评估模型的适用性的分析，利用Gamma分布对于设计定型试飞期间，军用飞机的失效率从浴盆曲线的早期故障阶段过渡到偶发故障阶段这一过程的良好符合性及分布的有界性，建立基于Gamma分布的军用飞机任务可靠性增长评估模型，并以某型军用飞机的任务可靠性评估为例，对该方法的工程适用性进行验证，结果表明：该方法可用于试飞阶段军用飞机任务可靠性增长评估。