CV模型在脑出血图像分割中的应用

初于成 张广材 张德睿 朱乐天 彭磊

山东第一医科大学（山东省医学科学院）

一、引言

脑出血是指非外伤性脑实质内血管破裂引起的出血，是一种常见的脑血管疾病，具有发病过程快、发病率高的特点。早期死亡率很高，幸存者中多数留有不同程度的运动障碍、认知障碍、言语吞咽障碍等后遗症。加强对脑出血疾病的辅助诊断和治疗，具有重要的意义。CT图像一直是医生诊断脑出血时依赖的重要手段。通过图像分割算法精确分割出血肿区域，测算出血肿体积，能够为脑出血的进一步分级和后续针对性治疗起到积极的作用。传统的方法是人工手动分割出CT图像中的病灶区域，这种临床测量手段主要依据医生的经验，主观性较强，分割过程极其耗时且异常艰辛，精确度及可重复性比较差。

图像分割是将图像划分为多个具有相似性特征区域的一个过程，是对医学图像中正常或是病灶区进行定性分析的一个关键步骤。基于CV活动轮廓模型[1-3]的图像分割方法可以同时利用图像的底层特征和高层信息，与传统图像分割方法相比，有着很强的优越性。CV模型是医学图像分割的一个重要的分割手段，对噪声大、灰度不均、边界模糊的图像分割，能够达到较理想的效果，满足分割精度高、速度快的要求。

二、CV模型

CV模型由Chan和Vese提出的基于水平集的图像分割算法[1-3]，其基本思想是利用轮廓曲线的内外灰度均值引导演化曲线收敛于目标边缘。假设Ω为图像区域，图像上坐标为(x,y)点的像素灰度值由I(x,y)来表示，C为演化曲线，该曲线内部的区域表示为Ωin、外部的区域表示为Ωout，则CV模型的能量函数定义为：

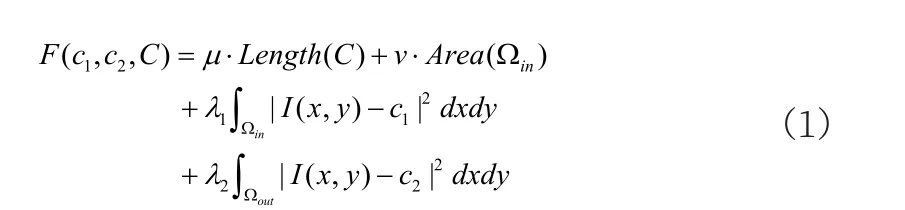
其中，Length(C)表示演化曲线C的长度，Area( Ωin)表示演化曲线包含区域的面积；c1和c2为拟合中心，分别用演化曲线内部与外部区域的灰度均值来表示；µ≥0，v≥0，λ1＞0，λ2＞0是固定参数。

在水平集方法中，用Lipschitz函数φ(x,y)的零水平集来表示演化曲线C。

定义Heaviside函数H和一维Dirac测度δ如下：

用H(φ)表示曲线C的内部区域，用1-H(φ)表示曲线C的外部区域，则能量函数F可以写为：

其中灰度均值c1和c2可以用下列公式求得：

在保持c1和c2不变的情况下，通过相应的Euler-Lagrange方程进行求解[4]，用人工时间t≥0参数化下降方向，用定义为初始轮廓）来表示演化曲线，可得到如下的演化方程：

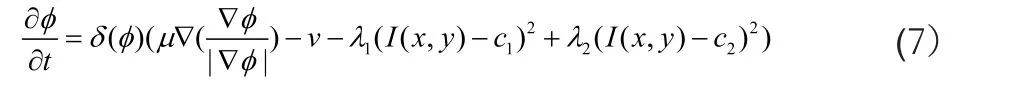
最小化上式可得到最优的零水平集，即最优轮廓。

三、脑出血CT图像的分割

将CV模型应用于脑出血病人的CT图像分割上，选取CT图像上血肿区域作为感兴趣区域。CV模型的参数这里取然后使用迭代优化的方式进行求解。分割效果如图1所示。

图1 基于CV模型的CT图像分割结果

四、结束语

CV模型是基于区域的水平集方法，在分割模糊边缘、异质、含噪图像时，其效果相对于其他基于模糊聚类、阈值、形态学等图像分割算法，具有较好的分割精度。因此，本文将CV模型用于脑出血CT图像的分割。利用CV模型能够准确分割出边界模糊的血肿区域，在辅助医生进一步进行血肿体积测算、脑出血程度诊断及后续治疗等方面具有积极意义。