弧齿锥齿轮基本参数优化设计
孙月海,唐二星
(天津大学机械工程学院机构理论与装备设计教育部重点实验室,天津300350)
弧齿锥齿轮是一种非常重要和复杂的传动齿轮,具有承载力大和传动平稳的优点,被广泛应用于汽车和航空航天工业中。弧齿锥齿轮是传动系统的重要元件,其设计依旧是研究热点,研究内容主要包括齿面设计方法和齿面接触性能优化两方面。
在齿面设计方法方面:Litvin等[1]提出了“局部综合法”;方宗德等[2]研究了基于传动误差设计的弧齿锥齿轮设计方法;周凯红等[3]发展了基于预定啮合特性的点啮合齿面设计方法;Wang等[4]基于局部综合法提出了齿面设计的全局综合法;Zhang等[5]提出了新的双螺旋切齿法。近年来,Ease-off齿面拓扑修正作为一个新的研究热点[6],为齿面主动设计提供了新方法。其相关研究成果不断涌现:曹雪梅等[7]实现了齿面啮合特性的预控;魏冰阳等[8]提出了Ease-off曲面综合法;张卫青等[9]分析了共轭差曲面的求取问题;严宏志等[10]研究了基于Ease-off的弧齿锥齿轮齿面分区修形方法。
在齿面接触性能优化方面:Zheng等[11]提出了变形齿面接触分析法;Achtmann、段路茜、钱学毅等[12-17]以不同的优化设计变量,建立了满足不同性能要求的多目标优化数学模型,为齿轮优化设计提供了参考。后续,许多学者又发展了基于齿面修形的性能优化方法:王琪等[18]以控制参数为优化变量,建立了以加载传动误差峰峰值和齿面最大接触应力最小为目标的弧齿锥齿轮齿面优化数学模型;蒋进科等[19]以修形曲面参数为优化变量,对基于Ease-off拓扑修形的准双曲面齿轮进行多目标优化设计,获得其满意的修形齿面。
综上可知,围绕渐缩齿弧齿锥齿轮,现有研究主要是以局部共轭原理为基础的设计与优化,而从本质上分析,局部共轭接触是基于传统的机械式机床加工运动的限制而提出和发展起来的[20],得到的齿面副理论上为点接触齿面,其实际接触区域小,使得齿面承载能力的提升受到较大限制。事实上,采用机床调整参数补偿技术可以实现齿面线接触[21]。对于全齿面线接触的齿轮副,须考虑其实现条件及接触性能,若要在理论设计阶段实现全齿面线接触以及优化齿面接触性能,则要对弧齿锥齿轮齿面副关键的基本参数进行优化设计。
针对上述研究中存在的不足,为扩大齿面的接触区域,实现全齿面接触和优化齿面接触性能,笔者提出了弧齿锥齿轮基本参数优化设计方法:首先,论证了采用机床调整参数补偿技术可以实现齿面线接触;其次,以弧齿锥齿轮基本参数为变量,建立全齿面线接触的弧齿锥齿轮齿面性能多目标优化数学模型,并运用现代多目标骨干粒子群优化算法,求得其最优基本参数;最后,进行具体算例的仿真分析,以验证优化方法的有效性。
1 齿轮副线接触实现方法
根据齿轮共轭啮合传动原理,当设定大轮齿面为已知的加工齿面时,按照公式(1),可得到与大轮齿面线接触共轭的小轮齿面,称为理论齿面Σ1,具体求解过程可参见文献[22]。
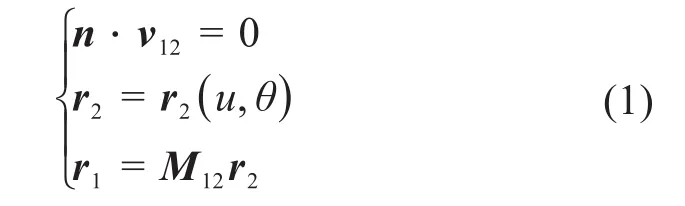
式中:n为大轮齿面的法矢量;v12为齿轮副的相对速度;r2(u,θ)为大轮齿面方程,u和θ为大轮齿面参数;r1为小轮齿面方程;M12为大轮坐标系到小轮坐标系的变换矩阵。
在传统的弧齿锥齿轮加工中,小轮齿面的加工方法是:根据格里森计算卡得到机床调整参数,然后将其代入切齿数学模型,得到一定加工方法下的小轮齿面方程[20]。小轮的加工齿面Σ1*是与大轮齿面点接触共轭的。
为实现小轮加工齿面Σ1*与大轮齿面线接触,须采用机床调整参数补偿技术来修整小轮的机床调整参数,使其加工齿面Σ1*逼近理论齿面Σ1。具体计算方法如下:
对小轮加工齿面Σ1*进行网格划分,由小轮的理论齿面Σ1与加工齿面Σ1*在所有网格点上对应的法向失配量组成其几何拓扑误差曲面,如图1所示,则小轮的理论齿面Σ1可由小轮的加工齿面Σ1*叠加几何拓扑误差曲面获得。
在小轮加工齿面坐标系中,机床调整参数记为d,加工齿面上任一网格点的位置矢量与法向矢量可分别表示为Ri1(εi,d)和ni1(εi,d),其中:εi为网格点i的坐标参数,i=1,2,…,m,m为齿面网格点总数。
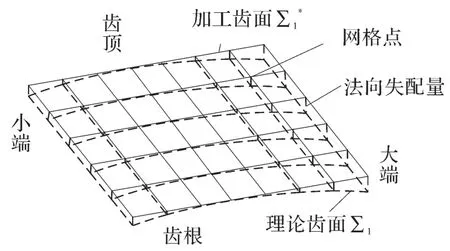
图1 小轮齿面的几何拓扑误差曲面Fig.1 Geometric topological error surface of pinion tooth surface
小轮齿面几何拓扑误差曲面上网格点对应的法向失配量hi可表示为:

式中:Ri为在小轮理论齿面Σ1上网格点的位置矢量。
以机床调整参数d为变量,以所有网格点法向失配量偏差平方和最小为目标,建立最小二乘法优化模型,即小轮齿面几何拓扑误差与小轮机床调整参数之间的补偿修整数学模型:
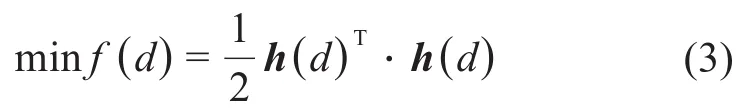
基于调整参数识别算法,采用基于置信域策略的列文伯格-马夸尔特迭代算法求解非线性最小二乘优化问题[20]。更新机床调整参数,使小轮加工齿面逼近理论齿面,进而实现在误差允许范围内的齿面线接触,其具体实现过程将另文详细阐述。
2 弧齿锥齿轮接触性能优化模型
在弧齿锥齿轮传动副中,全齿面接触的前提是小轮齿面与大轮齿面线接触共轭,且无根切和无干涉。根据一定的设计参数得到大轮齿面,基于第1节介绍的齿面实现方法,可得到与大轮齿面线接触的小轮齿面。为实现弧齿锥齿轮副的全齿面线接触,须考虑齿面排除啮合界限线和根切界限线(以下简称为“2类界限线”)以及齿顶变尖的影响。同时,齿轮副接触线的相对滑动速度须有利于动力润滑油膜的形成。因此,提升齿面润滑性能和承载能力是弧齿锥齿轮基本参数优化设计的两个衡量指标。
2.1 优化变量
齿坯基本参数中螺旋角β对齿面润滑性能和承载能力有较大影响,选择合适的话,可以保证齿面接触比达到1.25~1.75;工作齿高系数hk会显著影响2类界限线与齿面工作区的关系;变位系数ξ与齿轮接触强度和齿顶变尖关系密切。因此,选定螺旋角β、工作齿高系数hk、变位系数ξ作为优化设计变量,记为:

2.2 齿面约束条件
2.2.1 等式约束条件
1)啮合界限线。
根据文献[22]得到大轮齿面的啮合界限线方程为:

其中:
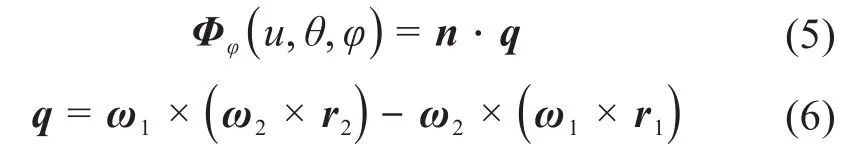
式中:φ为齿轮副的转角参数;ω1、ω2分别为小齿轮和大齿轮的角速度;q为啮合点处的线速度矢量。
啮合界限线将大轮齿面分为接触区和非接触区。大轮齿面接触区分布如图2所示。
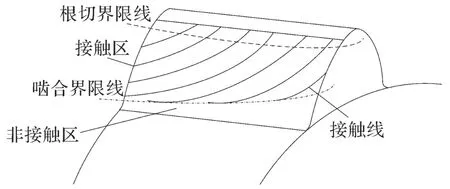
图2 大轮齿面接触区分布Fig.2 Distribution of contact area of large gear tooth surface
为实现弧齿锥齿轮全齿面接触,要求啮合界限线分布在大轮齿面区域外部下侧,即要求啮合界限线在轴截面上的旋转投影线分布在大轮齿根曲线旋转投影线下侧,如图3所示,图中阴影部分为大轮轴截面。设定大轮轴截面内轴向有从小端到大端4个均布的比较点(Pj,j=1,2,3,4)。根据这4个比较点在啮合界限线的旋转投影值Rfj与在齿根曲线的旋转投影值rfj的差值Rfj-rfj来判断啮合界限线是否在齿面区域内:如果不在区域内,Rfj<rfj,则差值之和为零;只要有任意一点在齿面区域内,则差值之和为正值。
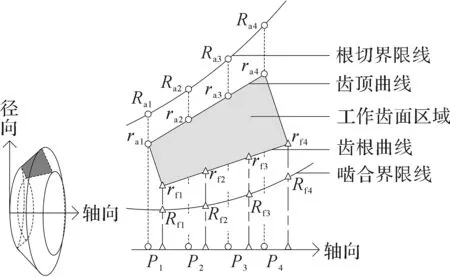
图3 大轮齿面啮合界限线和根切界限线旋转投影的分布Fig.3 Distribution of rotation projection of meshing limit line and root cutting limit line of large gear tooth surface
记第1个等式约束条件为:

2)根切界限线。
根据文献[22]得到大轮齿面的根切界限线方程为:
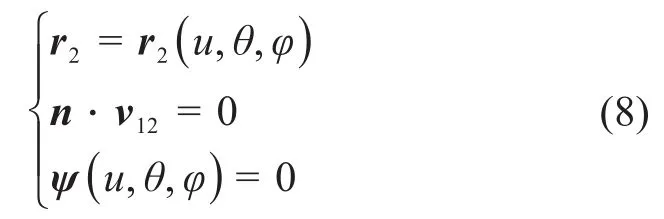
其中:
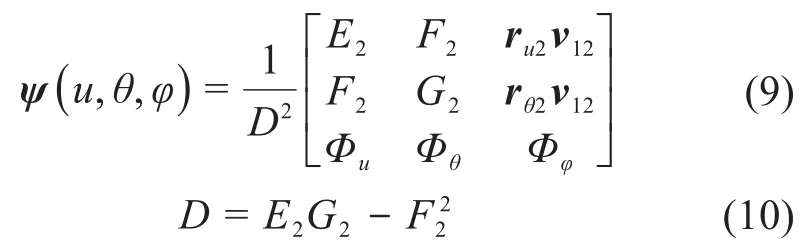
式中:E2、F2和G2分别为大轮齿面第一基本齐式的系数;ru2和rθ2分别为大轮位置向量对其齿面参数u和θ的偏导数;Фu、Фθ和Фφ分别为啮合函数Ф对其齿面参数u和θ和转角参数φ的偏导数。
当大轮齿面上存在根切界限线时,齿轮副啮合会使小轮出现根切或者产生啮合实体干涉。为实现弧齿锥齿轮的全齿面接触,要求根切界限线分布在大轮齿面区域外部上侧,如图3所示。其判定方法与啮合界限线判定方法相同,利用4个比较点在齿顶曲线的旋转投影值raj与在根切界限线的旋转投影值Raj的差值raj-Raj来判断根切界限线是否在齿面区域内:如果不在区域内,raj<Raj,则差值之和为零;只要有任意一点在齿面区域内,则差值之和为正值。
记第2个等式约束条件为:
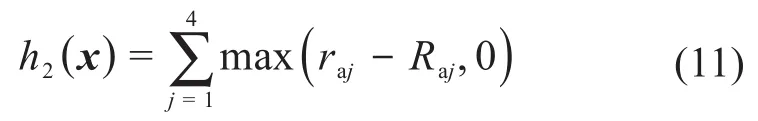
2.2.2 不等式约束条件
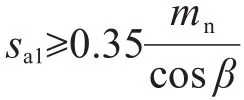
记不等式约束条件为:

2.3 齿面优化目标
1)齿面润滑性能。
可应用弹流动压润滑理论对弧齿锥齿轮传动弹流油膜厚度进行计算[23]。采用Hamrock-Dowson公式[24]计算最小油膜厚度Amin:

式中:α为润滑油黏压系数;η0为润滑油在某温度下的动力黏度;u0为卷吸速度;R为齿轮啮合点的当量曲率半径;E为齿轮材料的当量弹性模量;Q为齿轮啮合点的单位宽度接触载荷。
分析式(13)可知,除了一些实际工况参数,最小油膜厚度Amin与齿面理论设计相关的参数有卷吸速度u0和当量曲率半径R,因此将它们合并为综合参数[13]来评价齿面的润滑性能,记为:

当量曲率半径R的计算。根据文献[22],可得齿面啮合点处接触线法向量N为:
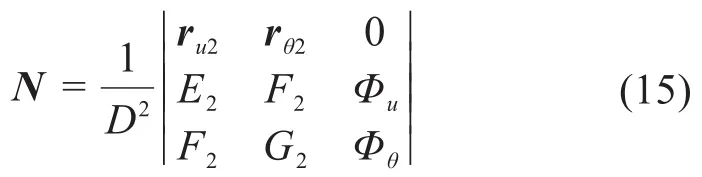
结合式(10)和式(15),推导得到当量曲率半径R的计算式如下:

卷吸速度u0的计算。设啮合点处两齿轮的速度分别为v1、v2,g12为齿轮副相对速度v12方向的单位矢量,则:
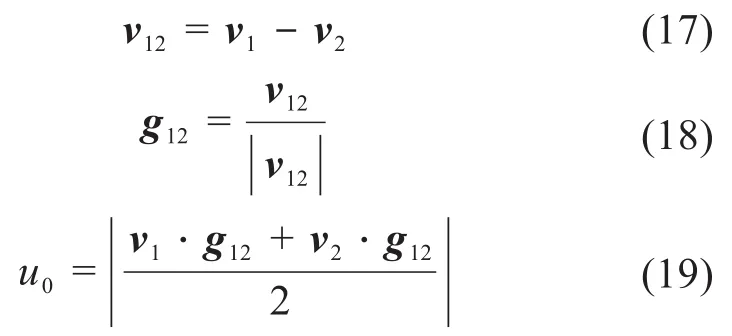
以齿面润滑性能综合参数vρ作为第1个优化目标,即在约束条件下,尽可能使所有齿面离散网格点的vρ较大,有利于保证齿面具有良好的润滑性能。建立第1个目标函数如下:
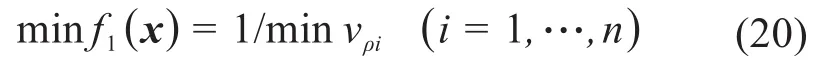
式中:n为齿面离散网格点数目。
2)齿面承载能力。
齿面承载能力可以用齿面瞬时接触线的总长度来衡量,瞬时接触线的总长越长,则齿面的承载能力越强。因此,在约束条件下,以同一齿面的所有瞬时接触线总长最大为第2个目标函数,即:

式中:T为单齿啮合时长;lt为t时刻齿面瞬时接触线总长度。
2.4 齿面接触性能多目标优化数学模型
构建以拓宽2类界限线、防止齿顶变尖为约束条件,以润滑性能综合参数和齿面瞬时接触线总长度最大为目标的齿面接触性能多目标优化数学模型。为了简化数学模型的计算过程,须将约束优化问题转换成无约束优化问题,为此,对2.2节中等式和不等式约束采用外点惩罚法进行处理,这样可使约束优化问题转换为附带惩罚项的无约束优化问题。结合式(7)、式(11)、式(12)、式(20)、式(21),建立齿面接触性能多目标优化数学模型:
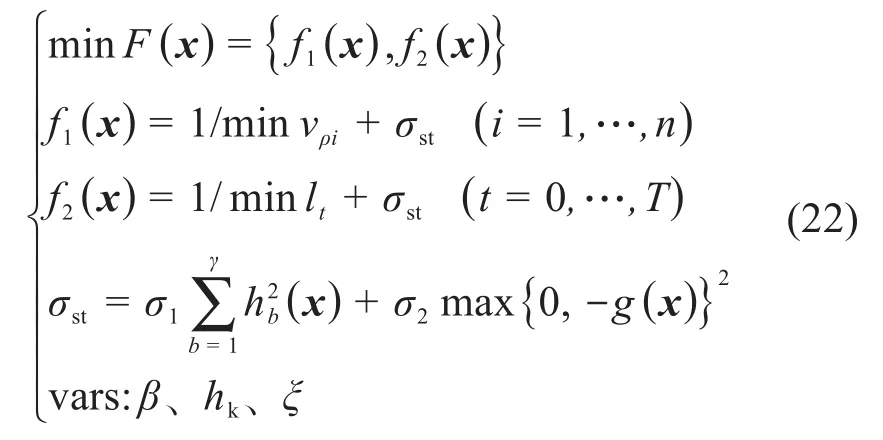
式中:γ为等式约束的数量,本文中γ=2;σ1、σ2为惩罚因子。
3 齿面接触性能多目标优化问题的求解
3.1 求解算法选择
针对齿面润滑性能综合参数和齿面瞬时接触线总长度最大的多目标优化问题,由分析可知:较大的螺旋角β和工作齿高系数hk可以加大齿面接触线长度,提升齿面承载能力,但齿面摩擦也会随之增大,所以该问题包含了互相冲突的目标函数,不具有唯一的最优解,那么就须寻找该问题的最优解集,然后再进行单一解的决策,选择恰当的解。
同时,在建立了齿面接触性能多目标数学模型后,针对参数多、计算复杂的多目标优化问题,如前文所述,在最优基本参数的求解上,无论是按照经验取值,还是进行大量的设计试算,都不可避免地面临巨大的工作量。本文构建的齿面润滑性能和承载能力的多目标优化数学模型是由啮合方程与目标函数构成的复合方程,梯度矩阵求解难度大。而现代进化算法因具有不需要梯度信息、自主学习能力强和收敛效果较好等特点,逐渐成为解决优化问题的有效手段。基于此,Zhang等[25]提出了一种多目标骨干粒子群优化算法,可以求解得到均匀分布的Pareto解。本文采用该方法对问题求解。
3.2 求解流程
结合式(22)与多目标骨干粒子群优化算法,采用图4所示的流程进行多目标优化数学模型的求解,最后输出设计参数的最优Pareto解集。

图4 齿面接触性能多目标优化数学模型的求解流程Fig.4 Solution process of multi-objective optimization mathematical model of tooth surface contact performance
4 算例分析
为了验证上述弧齿锥齿轮优化设计方法的可行性,以一对齿数比为29/11、中低速传动的弧齿锥齿轮为研究对象进行计算。设定大轮凸面和小轮凹面为工作面,齿轮副的几何参数见表1。大轮采用成形法加工[20],小轮采用变性法加工[20],且补偿小轮机床调整参数使得小轮齿面与大轮齿面线共轭接触。大轮刀盘参数见表2。
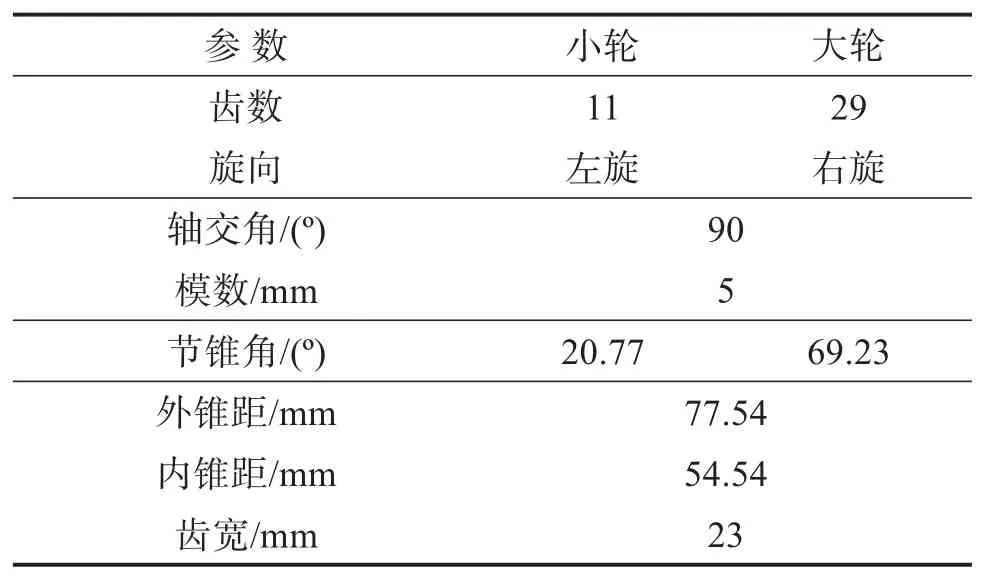
表1 弧齿锥齿轮副几何参数Table 1 Geometric parameters of spiral bevel gear pair

表2 大轮刀盘参数Table 2 Parameters of large gear cutter
参照式(22),建立齿面接触性能多目标优化数学模型:

根据各参数的数值,求解多目标优化数学模型,得到最优目标齿面基本参数。
设定终止迭代条件为200代,在迭代100代之后pareto前沿[25]基本不改变。到达终止条件后算例优化结果的Pareto前沿如图5所示。

图5 算例优化结果的Pareto前沿Fig.5 Pareto frontier of optimization results of example
为了使润滑性能综合参数和瞬时接触线总长度最优取值都比较均衡,选择图5矩形框中的点对应的一组设计参数作为基本参数优化方案,该方案的设计参数为[β*hk*ξ*]T=[35.07º1.70 0.48]T。按照传统的设计理论中查表取值的方法[20],取齿面设计参数[β hkξ]T=[35.00º1.65 0.39]T作为优化前基本参数。
把优化前后的基本参数分别代入齿面方程中,得到图6所示的大轮齿面接触线和图7所示的由大轮凸面包络出的小轮凹面,图6中标注了根切界限线的位置分布。
图6(a)表明:优化前大轮齿面上存在根切界限线,大轮凸面在包络出小轮凹面时,大轮大端齿顶部分进入小轮齿面实体内,造成根切(或干涉),如图7(a)局部放大所示;图6(b)表明:在齿形参数优化后,大轮齿面上不存在根切界限线,大小轮齿面均在实体外部啮合,无根切现象,如图7(b)局部放大所示。同时,在基本参数变量范围内,无论是否经过优化,啮合界限线均不在大轮工作齿面区域内。
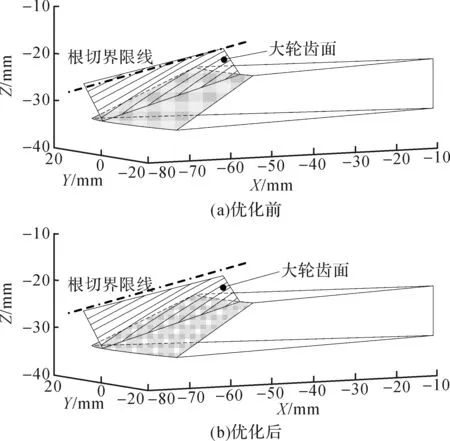
图6 大轮齿面接触线示意Fig.6 Schematic of contact line of large gear tooth surface
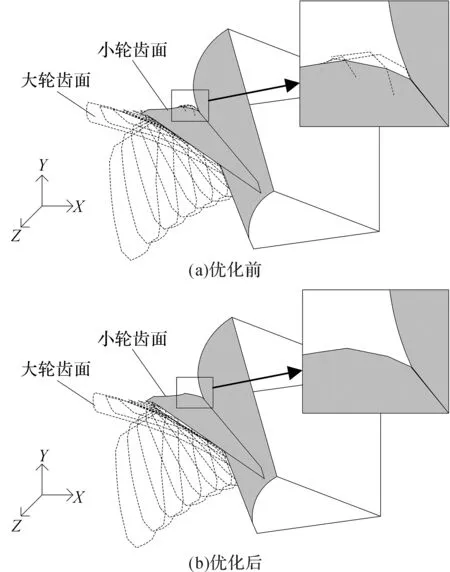
图7 大轮凸面包络出的小轮凹面Fig.7 Pinion tooth surface generated by large gear tooth surface
对于齿面接触性能的评价,齿面离散网格点的润滑性能综合参数最小值和齿面瞬时接触线总长度最小值见表4。
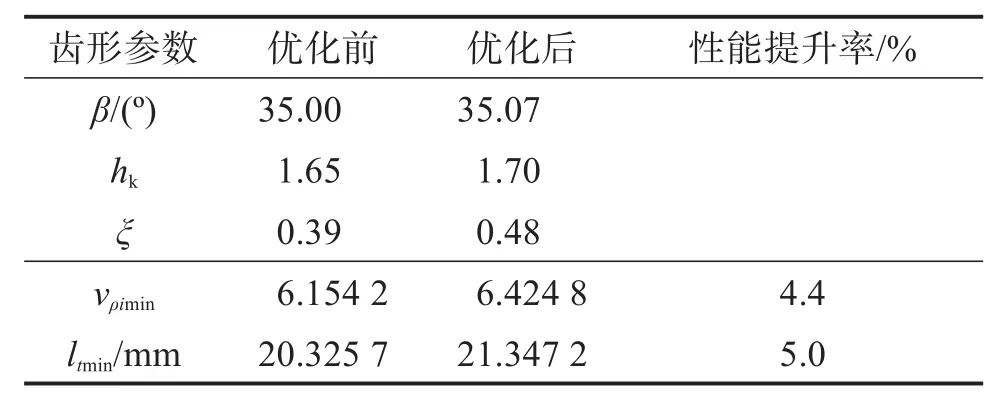
表4 齿面离散网格点的润滑性能综合参数最小值和齿面瞬时接触线总长度最小值Table 4 The minimum values of lubrication performance comprehensive parameter and total length of instantaneous contact line on the tooth surface of discrete mesh points
由表4可知:优化后齿面润滑性能比优化前提升了4.4%,优化后承载能力比优化前提升了5.0%。由此可见,对齿轮基本参数进行优化设计,能够提升齿面的润滑性能和承载能力。
将优化前后得到的弧齿锥齿轮基本参数代入齿面方程中分别进行齿面点求解,建立齿轮副三维模型,并应用有限元软件进行仿真分析,得到如图8所示的弧齿锥齿轮齿面接触仿真结果。由图8(a)可知,基本参数优化前,由于根切界限线在大轮齿面内,在实体啮合时大轮大端齿顶处与小轮齿根处产生干涉,出现应力集中,这也印证了图7(a)局部放大部分所示的结果。由图8(b)可知,基本参数优化后,工作齿面内无2类界限线影响,因此齿面呈线接触,对应了图7(b)所示的包络效果。有限元仿真结果证实了理论设计的正确性。

图8 弧齿锥齿轮齿面接触仿真结果Fig.8 Simulation results of tooth surface contact of spiral bevel gears
5 结论
1)长期以来弧齿锥齿轮的设计及优化主要以局部共轭点接触齿面为基础,无法发挥全齿面承载接触的优势。针对此问题,本文以大轮加工齿面为已知齿面,通过引入小轮机床调整参数补偿技术,使小轮加工齿面向与大轮齿面共轭的理论齿面逼近,实现了弧齿锥齿轮副齿面线接触的设计。
2)全齿面线接触弧齿锥齿轮副受到2类界限线、齿顶变尖的影响,为此笔者提出弧齿锥齿轮基本参数优化设计方法。以螺旋角、工作齿高系数、变位系数为变量,在排除2类界限线和防止齿顶变尖的约束下,对表征润滑性能和承载能力的两优化目标进行数学建模,并引入现代多目标粒子群优化算法进行求解,获得了弧齿锥齿轮齿面副最佳基本参数。
3)通过对一个具体的弧齿锥齿轮展开基本参数的优化设计、数值计算、啮合状态仿真和有限元分析,结果表明,优化后的齿轮副呈全齿面线共轭接触,且接触性能得到明显提升,说明本文提出的设计方法切实有效。研究结果为弧齿锥齿轮的优化设计提供了新思路,具有一定的指导意义。

