三维点云的两步校准法及其应用研究

汪 威，张开颜，刘亚川，黄玉春

（1.湖北工业大学机械工程学院，湖北武汉430068；2.武汉大学遥感信息工程学院，湖北武汉430072）

点云校准是指先获取待处理点云与标准点云的相对位姿，再将待处理点云进行平移和旋转变换后，使其与标准点云位姿相同的过程。大部分文献将点云位姿测算及相应的刚体变换过程称为点云配准，其中应用最广泛的是由Besl等［1］提出的迭代最近点（iterative closest point，ICP）法，该方法利用最近点对的欧式距离对点云间的变换矩阵进行动态最小二乘拟合，其配准精度极高。但是，为了避免在匹配点对过程中陷入局部最优，要求2个点云的相对位姿不能太大，故在实际应用中通常先对点云进行粗配准，在得到接近位姿后再用ICP法进行精配准［2-3］。

点云粗配准依赖于点云特征参数的选取［4-6］。Rusu等［7］将小范围内点与点之间的夹角、距离等几何信息转换为高维度的点特征直方图（fast point feature histograms，FPFH），并将其作为点云特征参数，但由于FPFH的维度较高，使得点对匹配过程的运算量较大［8］。张广鹏等［9］利用主成分分析法求得了点云的主轴坐标系，并将其作为人脸点云的特征参数，但是，该方法的求解效果依赖于点云外形的对称性。Stoyanov等［10］对点云所在空间进行网格划分，选取其中某一片点云为模板并构建高斯混合模型，以其作为点云特征参数。张琮毅等［11］根据点云的颜色，采用不同点云特征参数对特征空间进行初始匹配：对于无颜色的点云，计算其FPFH作为特征参数；对于有颜色的点云，计算其方向直方图签名作为特征参数。

然而，上述点云粗配准方法在选取、匹配特征参数时运算量过大，导致其执行效率难以满足实际应用的要求。因此，本文以具有平面特征的工件的三维点云为研究对象，提出了一种三维点云两步校准法：在不损失精度的前提下，利用密度聚类算法提取平面特征，并结合二维图像模板匹配算法实现点云的快速校准。最后将提出的三维点云两步校准法应用于高压输电线塔塔座自动焊接系统，以识别塔座的位姿信息。

1 三维点云两步校准法的原理分析

1.1 特征参数选取

机械零件常常包含具有平面、球面和圆柱面等几何特征的多个表面。通过激光扫描得到机械零件的三维点云，再利用统计学方法提取点云中的某些几何特征是点云位姿测算的有效手段之一。以具有平面特征的工件的三维点云为研究对象，对两步校准法的原理进行分析。首先，从三维点云中随机选取3个点：A（Ax，Ay，A）z、B（Bx，By，B）z和C（Cx，Cy，C）z，利用式（1）计算由上述3个点构成的三角形的面积S，并基于平面矢量法建立3个点在直角坐标系内xoy平面上的投影位置与三角形面积S之间的关系，如图1所示。由式（1）可知，投影点的位置排序决定了三角形面积S的正负性。

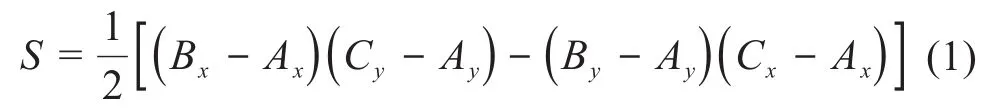
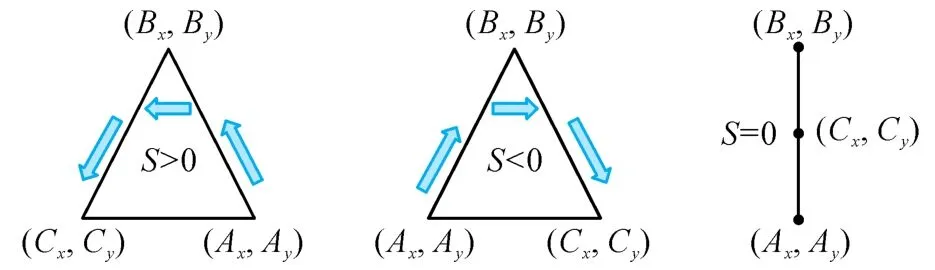
图1 xoy平面内投影点的位置与三角形面积的关系Fig.1 Relationship between position of projection point and triangle area in xoy plane

根据S的正负性对投影点进行顺时针排序：首先，输入随机选取的3个点在xoy面内的投影点集合P；然后，根据投影点的x坐标，按由小到大的顺序对投影点进行排序，设排序后的投影点集合I={A ，B，C} ；最后，将I中各点的坐标代入式（1），计算得到三角形面积S，若S＜0，交换I中B和C的位置索引。

完成投影点排序后，计算I中3个投影点所在平面的单位法向量。因I中3个投影点为顺时针排列，故可确定该单位法向量的方向。对工件的三维点云进行n（n为大于1的任意整数）次抽样后，得到平面单位法向量集合F={F1，F2，…，Fn} 。

但是，在获取工件点云的过程中，激光三维轮廓传感器多是沿垂直于工件主平面的方向进行扫描，导致所采集的工件主平面的点云密度比其他平面的大，故点云中任意不共线的三点所在平面的单位法向量趋近于主平面的单位法向量V。针对这一现象，本文采用密度聚类算法从平面单位法向量集合F中提取V［12-13］。为阐述提取原理，引入以下概念。

定义下标变量i、j、k为F中元素的位置索引，变量Nmin为密度阈值，ε为半径参数。

定义Fi的ε-邻域集合为Nε（F）i，Nε（F）i={Fj∈F|dist(Fj，Fi)≤ε}，其中dis（t）为计算两点间欧式距离的函数，|Nε（F）i|表示Fi的ε-邻域集合中的元素个数。

核心点：对于Fi∈F，若其ε-邻域集合中的元素个数|Nε（F）i|≥Nmin，则Fi为核心点。

密度直达：若Fj∈Nε（F）i，且Fi为核心点，则称Fj与Fi关于ε和Nmin密度直达。

密度可达：对于集合F，若任意Fi与Fi+1关于ε与Nmin密度直达，则F1与Fn关于ε和Nmin密度可达。

密度相连：对于 Fi与 Fj，若存在核心点 Fk使Fi与Fk及Fj与 Fk均关于ε和 Nmin密度可达，则称Fi与 Fj密度相连。

图2为密度聚类算法的原理示意图，其中三角形样本点为核心点，Nmin=5。所有与某核心点密度直达的圆形样本点在该核心点的ε-邻域范围内构成一个点簇，而不在核心点ε-邻域范围内的样本点则定义为噪声。若某一个点簇的邻域半径内存在另一个点簇，则这2个点簇密度相连，将其合并为一个点簇。通过合并，点簇的边界可以不断扩展。

图2 密度聚类算法的原理示意图Fig.2 Schematic diagram of principle of density clustering algorithm

采用密度聚类算法从点云的平面单位法向量集合F中提取主平面的单位法向量V。算法的输入为平面单位法向量集合F、半径参数ε和密度阈值Nmin，输出为主平面的单位法向量V，具体程序如下。

1.2 点云倾斜度校正

令激光三维轮廓传感器的扫描主平面为xoy平面，纵向测量方向为z轴方向。按右手定则建立基坐标系oG-xGyGzG，另定义一个初始位置与基坐标系oG-xGyGzG完全重合的刚体坐标系oB-xByBzB。将工件主平面单位法向量与基坐标系的xoy面单位法向量（即z轴）的夹角θ定义为两平面间的倾斜度。

通过密度聚类算法确定工件主平面单位法向量V=（Vx，Vy，Vz）。设Vstd为标准位姿模板图像主平面的单位法向量（目标向量），Vstd=（0，0，1），则Vstd与V的夹角θ可由式（2）求得。

通过变换矩阵GRB实现点云的倾斜度校正。设BP为点云在刚体坐标系oB-xByBzB中的坐标，GP为经倾斜度校正后点云在基坐标系oG-xGyGzG中的坐标。在点云倾斜度校正过程中，定义点云绕x轴的旋转角为α，绕y轴的旋转角为β。则有：

其中：

式中：versθ=1-cosθ

可得：

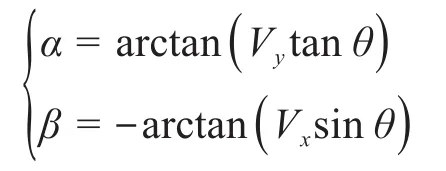
1.3 点云的位置与方向校准

基于点云中各点的高度（z坐标），将经倾斜度校正后的点云转换为点云灰度图，转换公式为：

式中：GPx、GPy和GPz分别为点云中各点在基坐标系中的坐标；Su、Sv分别为点云灰度图在宽度方向和高度方向上的量化因子；uP、vP分别为点云中各点在点云灰度图中对应的像素坐标；（fuP，vP）为灰度图中像素点（uP，vP）的灰度。

设标准点云的灰度图为模板，其像素坐标的集合M={Mx，My}，待处理点云灰度图的像素坐标集合D={Dx，Dy} ，其中Mx、Dx和My、Dy分别表示点云中各点x、y坐标对应的点云灰度图中像素坐标的集合。则点云在主平面内进行位置和方向校准时的变换矩阵G满足：

式中：dx、dy为点云沿x、y方向的平移量；γ为点云绕z轴的旋转角。

采用图像模板匹配算法求解变换矩阵G［14-15］。先求解点云灰度图各像素点的梯度响应值g(uP，vP)，再设置合适的阈值获取点云灰度图中具有较大灰度梯度的像素点，即边缘像素点。

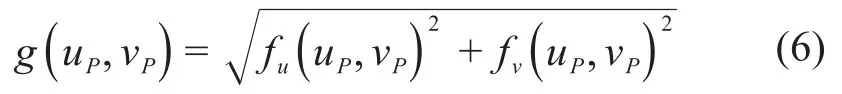
设标准点云灰度图的边缘像素点坐标的集合为m，待处理点云灰度图的边缘像素点坐标的集合为d。当m与d中的像素点正确匹配时，可确定变换矩阵G，此时两像素点集间欧式距离和SD达到最小。

设置迭代次数为K，利用式（7）求解变换矩阵G，具体步骤如下：

步骤1：在m中搜索d的最近点作为匹配点。

步骤2：基于得到的所有匹配点，利用式（7）得到估计变换矩阵GK。

步骤3：应用估计变换矩阵GK对边缘像素点进行变换，得到新的边缘像素点坐标的集合mK-1=GKmK。

步骤4：设置阈值δ，若满足|SDK-1-SDK|＜δ，令G=GK，并利用式（5）计算点云的平移量dx、dy与旋转角γ；否则K=K-1，返回步骤1）直到满足阈值条件或K=1。

2 三维点云两步校准法的应用与验证

2.1 高压输电线塔塔座位姿测量

高压输电线塔塔座由多块板件焊接而成。在焊接前，将塔座各板件通过点焊固定在一起，并置于自动焊接系统的工作台上，如图3（a）所示。由于塔座各构件的一致性较差，每次焊接前均需要进行人工示教，导致焊接效率较低，因此设计了一套可在线识别塔座位姿的自动焊接系统，可为焊接机器人提供路径规划的依据，其结构如图3（b）所示。在该自动焊接系统中，固定在工作台上方的激光轮廓传感器通过扫描得到待焊接塔座的三维点云，然后基于标准塔座的点云（通过扫描处于标准位姿的塔座得到），利用两步校准法对采集的三维点云进行校准，获取待焊接塔座的相对位姿。所设计的高压输电线塔塔座自动焊接系统的工作流程如图4所示。

图3 高压输电线塔塔座自动焊接系统及其结构组成Fig.3 Automatic welding system for tower base of high-voltage transmission line and its structure composition

选用的激光轮廓传感器的型号为KEYENCE LJ-V7200。在扫描过程中，x轴方向的采样间距为100 μm，y轴方向的采样间距为50 μm，采样速率约为1.56 m/s。工控机配置CPU Intel i5-6500，内存为8 G的Windows7 64位操作系统。利用激光轮廓传感器扫描高压输电线塔塔座并完成数据预处理，得到的三维点云的样本点总数Nt≈34 000个。

图4 高压输电线塔塔座自动焊接系统工作流程Fig.4 Working process of automatic welding system for tower base of high-voltage transmission line

2.2 抽样次数优化与主平面单位法向量提取

图5为对高压输电线塔塔座点云抽样500，2 500，12 500次时获得的平面单位法向量集合F的散点分布情况。由图5可知，随着抽样次数的增加，点簇的聚集效应趋于明显，即抽样次数n=12 500时，平面单位法向量集合的分布具有较好的集聚效果。但抽样次数过多会导致数据处理时间过长，过少则将影响位姿识别精度。因此选择合理的抽样次数是采用密度聚类算法提取主平面单位法向量V时的重要环节。

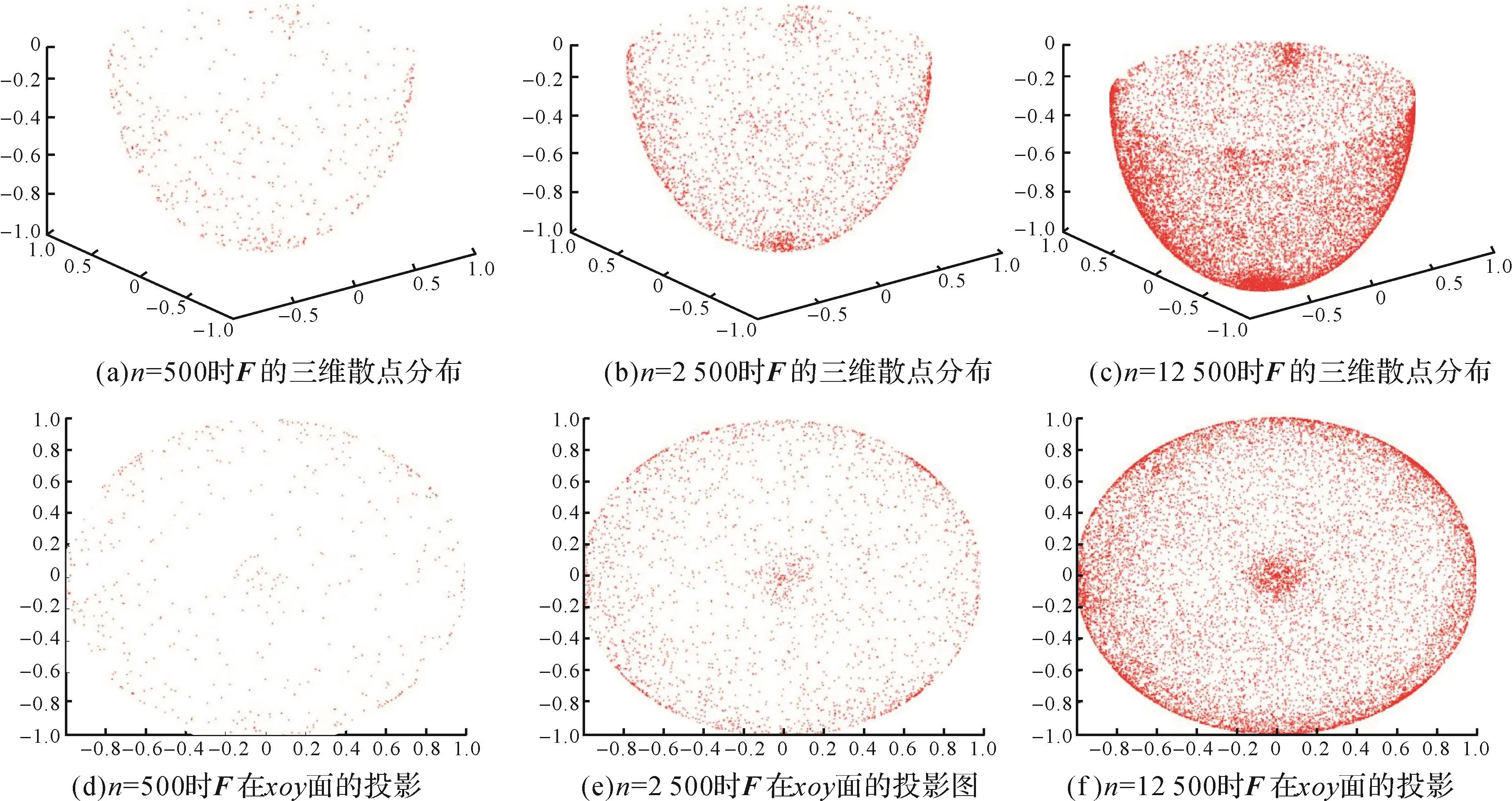
图5 抽样次数不同时平面单位法向量集合的散点分布情况Fig.5 Scattered distribution of unit normal vector set of plane under different sampling times

为得到最优的抽样次数，定义抽样次数n与点云中样本点总数Nt的比值为w。图6为w对5组高压输电线塔塔座点云对应的主平面单位法向量V的聚类效果的影响。由于V为单位向量，其变化量可用变换前后末端点间的距离Dtan来表征。由图6可知，随着w的增大，高压输电线塔塔座主平面的单位法向量V的变化量趋于收敛；当w≥0.38时，Dtan趋近于0。

2.3 高压输电线塔塔座位姿识别实验

设置抽样次数n=13 000，密度聚类算法中的参数ε=0.015，Nmin=20。利用两步校准法对高压输电线塔塔座的位姿进行识别。图7为倾斜度校正过程中位姿不同的高压输电线塔塔座点云。

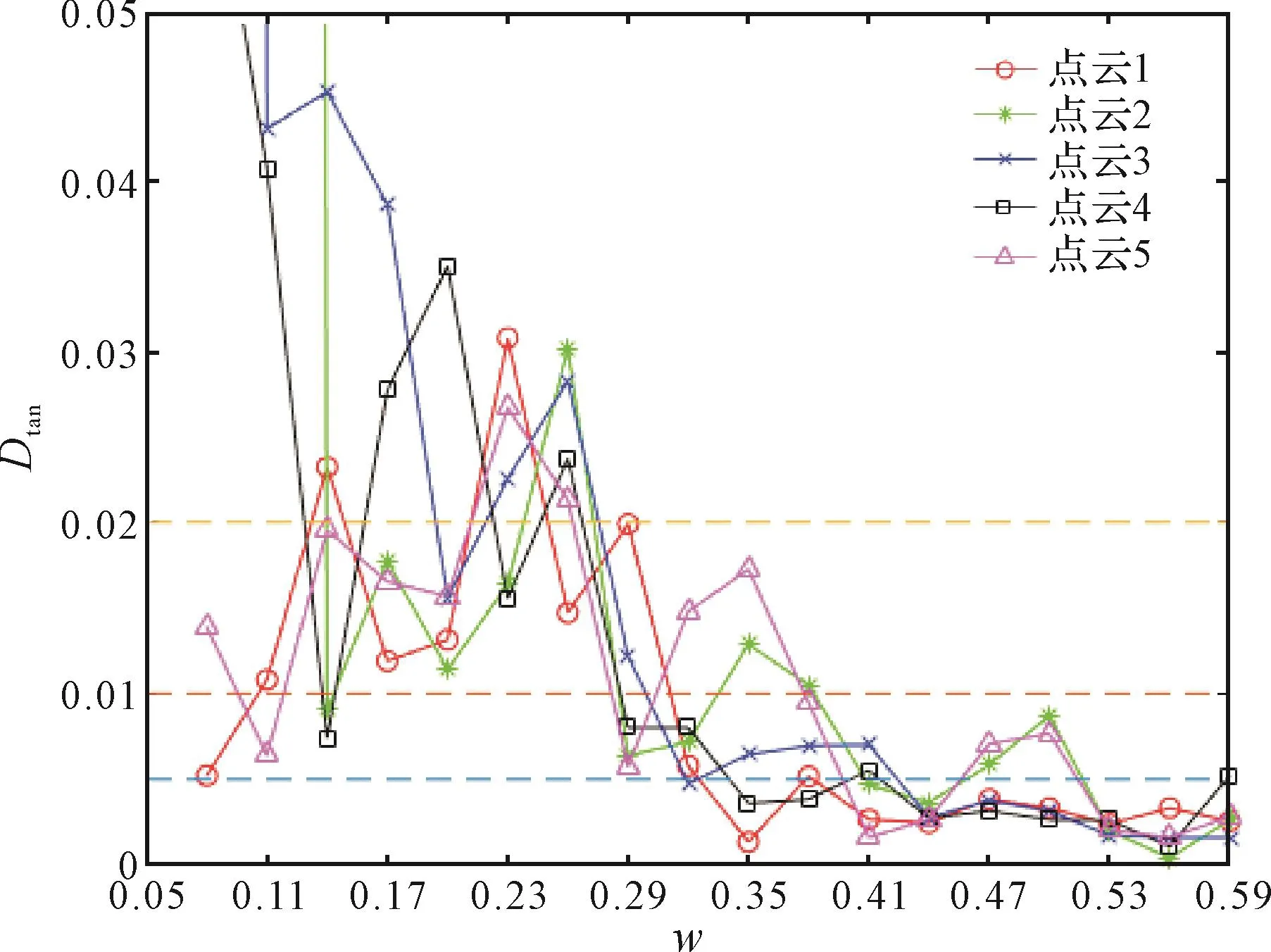
图6 w对主平面单位法向量聚类效果的影响Fig.6 Influence of w on clustering effect of principal plane unit normal vector

图7 倾斜度校正过程中位姿不同的高压输电线塔塔座点云Fig.7 Point clouds of tower base of high-voltage transmission line with different poses during inclination correction

利用式（4）将图7（a）、图7（c）对应的点云转换为点云灰度图，并利用1.2节中的公式获取待处理点云与标准点云的相对位姿，即平移量dx、dy与旋转角γ，如图8所示。

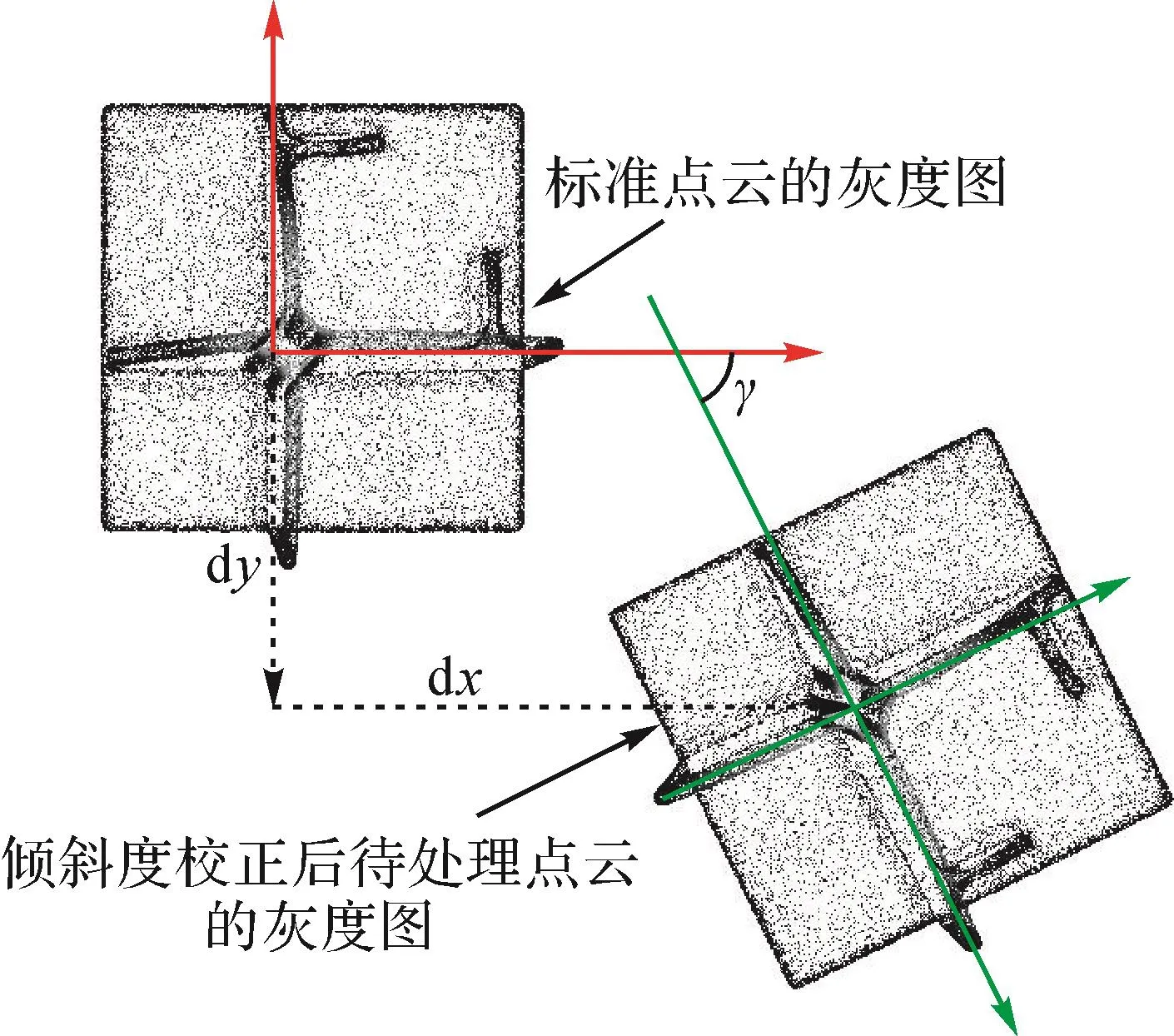
图8 待处理点云与标准点云的相对位姿Fig.8 Relative pose between pending point cloud and standard point cloud

为了测试两步校准法对高压输电线塔塔座位姿识别的精度、稳定性以及耗时，对8组位姿不同的塔座点云进行校准。各组点云的理论相对位姿参数如表1所示，其中第1组为标准点云，第2至第7组为待处理点云。

表1 8组点云的理论相对位姿参数Table 1 Theoretical relative pose parameters of eight groups of point cloud

利用两步校准法获得待处理点云的相对位姿参数，并计算其与理论相对位姿参数的残差，结果如表2所示。

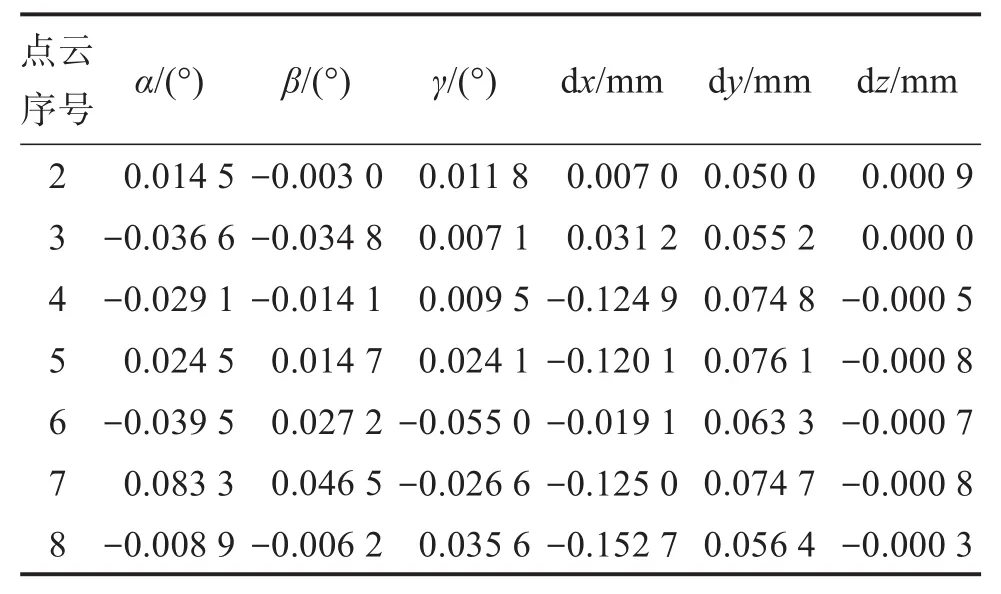
表2 基于两步校准法的点云位姿校准残差Table 2 Residuals of pose alignment for point cloud based on two-step alignment method

由表2可知，基于两步校准法获得的点云旋转角的最大误差约为0.1°，平移量的最大误差约为0.2 mm。表3为利用两步校准法校准点云位姿的耗时。由表3可知，利用两步校准法校准点云位姿的最长耗时约为9 s。

表3 基于两步校准法的点云位姿校准耗时Table 3 Time-consuming of pose alignment for point cloud based on two-step alignment method

采样一致性法是一种在实际工程应用中较为常用的粗配准算法［16］。为了验证本文两步校准法的实用性，选用点云算法库（point cloud library，PCL）中的采样一致性法对8组位姿不同的高压输电线塔塔座点云进行校准，校准残差和耗时分别如表4和表5所示。

表4 基于采样一致性法的点云位姿校准残差Table 4 Residuals of pose alignment for point cloud based on sample consensus method

表5 基于采样一致性法的点云位姿校准耗时Table 5 Time-consuming of pose alignment for point cloud based on sample consensus method

由表4和表5可知，基于采样一致性法获得的点云旋转角的最大误差约为1.6°，平移量的最大误差约为7.0 mm，最长耗时为38 s。

根据上述结果可知，在对具有平面特征的工件进行位姿识别时，本文提出的两步校准法能够较准确地获得工件的相对位姿变化信息，且在耗时上比采样一致性法约缩短了76%。

3 结 论

1）针对具有平面特征的工件的位姿识别，提出了一种基于倾斜度校正与图像模板匹配算法的三维点云两步校准法。通过顺时针排序与密度聚类算法，解决了点云特征参数的选取问题。

2）通过分析抽样次数对点云特征参数提取的影响，得到了最优抽样次数的选择规律，为两步校准法在实际工程中的应用提供了依据。

3）将两步校准法应用于高压输电线塔塔座自动焊接系统，对塔座位姿进行识别，并与基于采样一致性法的位姿识别结果进行对比。实验结果表明两步校准法在识别具有平面特征的工件的位姿时优于采样一致性法。

研究结果表明本文提出的三维点云两步校准法法在先进制造与智能检测领域具有广阔的应用前景。后续将在已有基础上，通过提取点云的母线、曲率和信息熵等特征来进一步确定点云的位姿。将方法的适用对象从平板类工件扩展到含曲面的工件，并结合人工智能算法进一步提高算法的快速性和适应性。