基于IGPS和麦克纳姆轮的AGV导航控制系统设计
王 颜,刘净瑜,李 光,张加波,刘 星,周欣欣
(北京卫星制造厂有限公司,北京100094)
最近四五十年来,工业自动化技术发展迅速,物流业和制造业发生了巨大变化。随着自动导引车(automated guided vehicle,AGV)技术的不断突破,生产成本得以降低,整体工作效率得到提高[1]。随着导航技术、传感器技术、网络通信技术、计算机仿真技术的发展,高端制造业必将转型升级,以实现人机交互、协调合作为目标的智能工厂及智能制造成为今后制造业发展的必然趋势。AGV作为一种全向智能移动平台,为智能工厂的精准配送、智能物流提供了有效的解决方案。AGV有多种导引方式,主要为磁导航、惯性导航、激光导航、视觉导航、基于传感器数据的导航、全球定位系统(global positioning system,GPS)导航、室内GPS(indoor GPS,IGPS)导航、光电编码器导航和无线射频识别导航等[2]。
目前,诸多研究人员对AGV导引技术进行了大量研究。张晓霞等[3]提出了一种GPS/DR组合导航定位算法,实现了对室外AGV的导航,但其定位精度不高且无法满足室内导航的精度要求。朱从民等[4-6]基于多传感器及多种导航技术建立了AGV导航控制系统,但是其定位精度也无法满足辅助装配的定位精度要求;夏凌楠等[7]提出了一种基于惯性传感器和视觉里程计的定位算法,实现视觉辅助定位,弥补了惯性导航的不足,但仍然无法实现后期AGV位置的修正。本文提出了一种基于IGPS和麦克纳姆轮的AGV精确定位和导航方法:首先,通过IGPS接收器与发射站的组网几何模型得出接收器的位置坐标;其次,通过多个接收器与快速矩形拟合算法得到AGV中心实时位姿信息(坐标值和姿态角),同时根据路径信息采用模糊PI(proportion integration,比例积分)算法实现路径的自动纠偏。
1 基于IGPS的AGV导航控制方法
1.1 AGV模型
本文研究的AGV的模型如图1所示。该AGV由可全方位移动的4个麦克纳姆轮驱动,其运动方式灵活多变,可应用于空间有限和高精度定位的场合;4个IGPS接收器安装于车体四角,其对角中心与车体中心重合。
该AGV导航控制系统主要由IGPS空间定位系统、导航控制器及驱动控制器三部分构成。IGPS空间定位系统中,发射站产生的2个扇形激光平面对整个测量空间进行扫描,安装在车体四周的IGPS接收器接收激光信号来实现车体的全局精确定位,获得其在指定世界坐标系下的空间位置坐标;导航控制器在获得车体空间位置坐标值后进行坐标转换,得出车体中心在厂房二维平面坐标系下的坐标值,并进行连续实时路径纠偏;驱动控制器则根据角速度、偏航角和速度值实时控制AGV在二维平面内任意方向的移动。
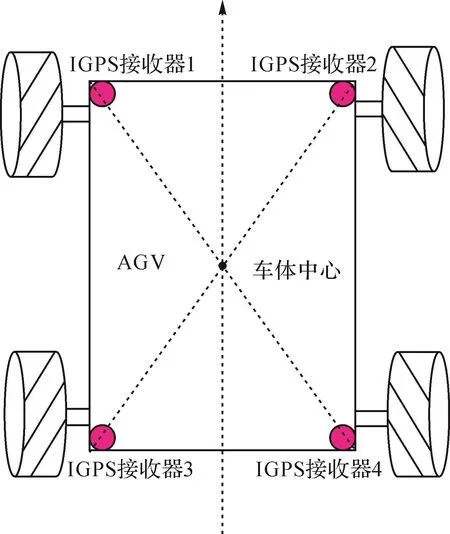
图1 AGV模型Fig.1 AGV model
1.2 基于IGPS的待测点位置坐标的确定
IGPS发射站的几何模型及其坐标系如图2所示。当发射站绕Z轴以ω速度转动时,每转1周便会产生一个基准时间值,作为后续每周测量的时间原点,其所对应的角度为360°。记发射站旋转第k周时的时间原点为tzk,激光平面1(LP1)、激光平面2(LP2)通过待测点p时,接收器各产生一个脉冲信号,此信号对应的时间信号tp1k、tp2k与时间原点tzk的差值记为t1k、t2k,称为特征时间,如图3所示。由t1k、t2k以及ω便可确定激光平面通过p点时在发射站坐标系O-XYZ下的所在平面。由2个平面就可确定待测点在发射站坐标系O-XYZ下所在的直线,由多个发射站就可以确定待测点的位置坐标。激光平面与被测点的位置关系如图4所示。
如图4(a)所示,通过单发射站测量时,n1=[n11n12n13],n2=[n21n22n23],分别为激光平面LP1、LP2的单位法向矢量,其中n11、n12、n13,n21、n22、n23分别为LP1和LP2在O-XYZ坐标系下的平面方程系数;Δd为LP2在Z轴上的截距,LP1在Z轴上的截距始终是0。以上参数均可提前标定。可得单发射站下待测点pi的坐标值,表示为[8-9]:
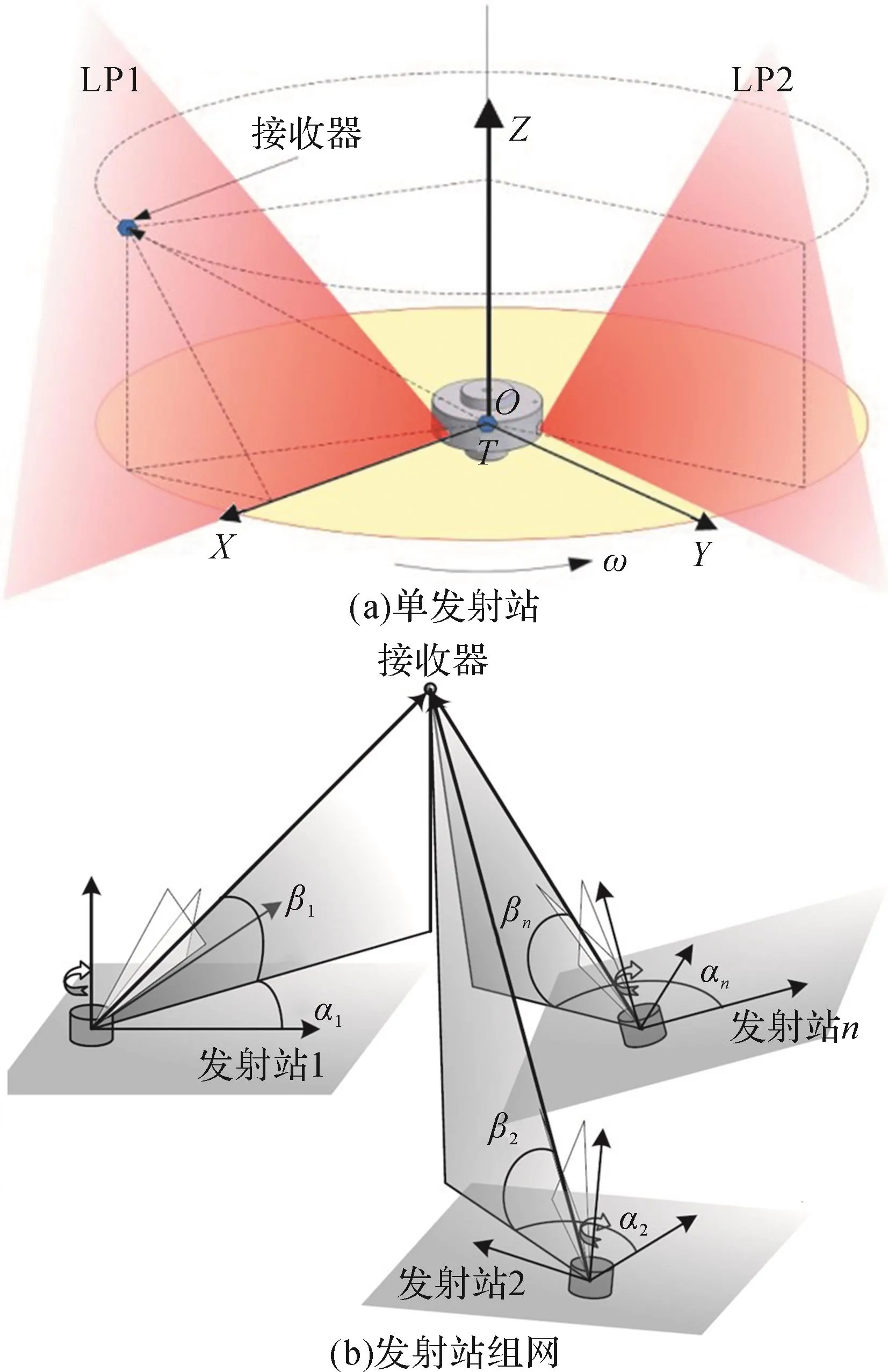
图2 IGPS发射站的几何模型及其坐标系示意Fig.2 Geometric model of IGPS transmitting station and diagram of its coordinate system
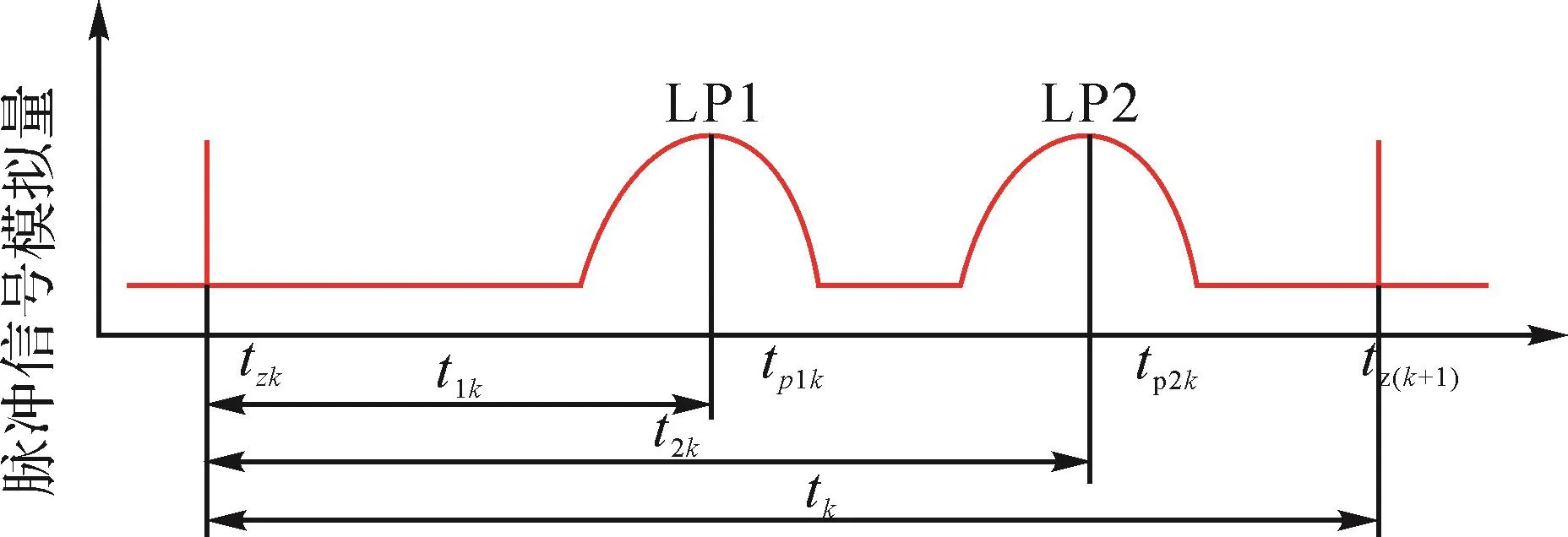
图3 IGPS接收器特征时间示意Fig.3 Diagram of IGPS receiver characteristic time
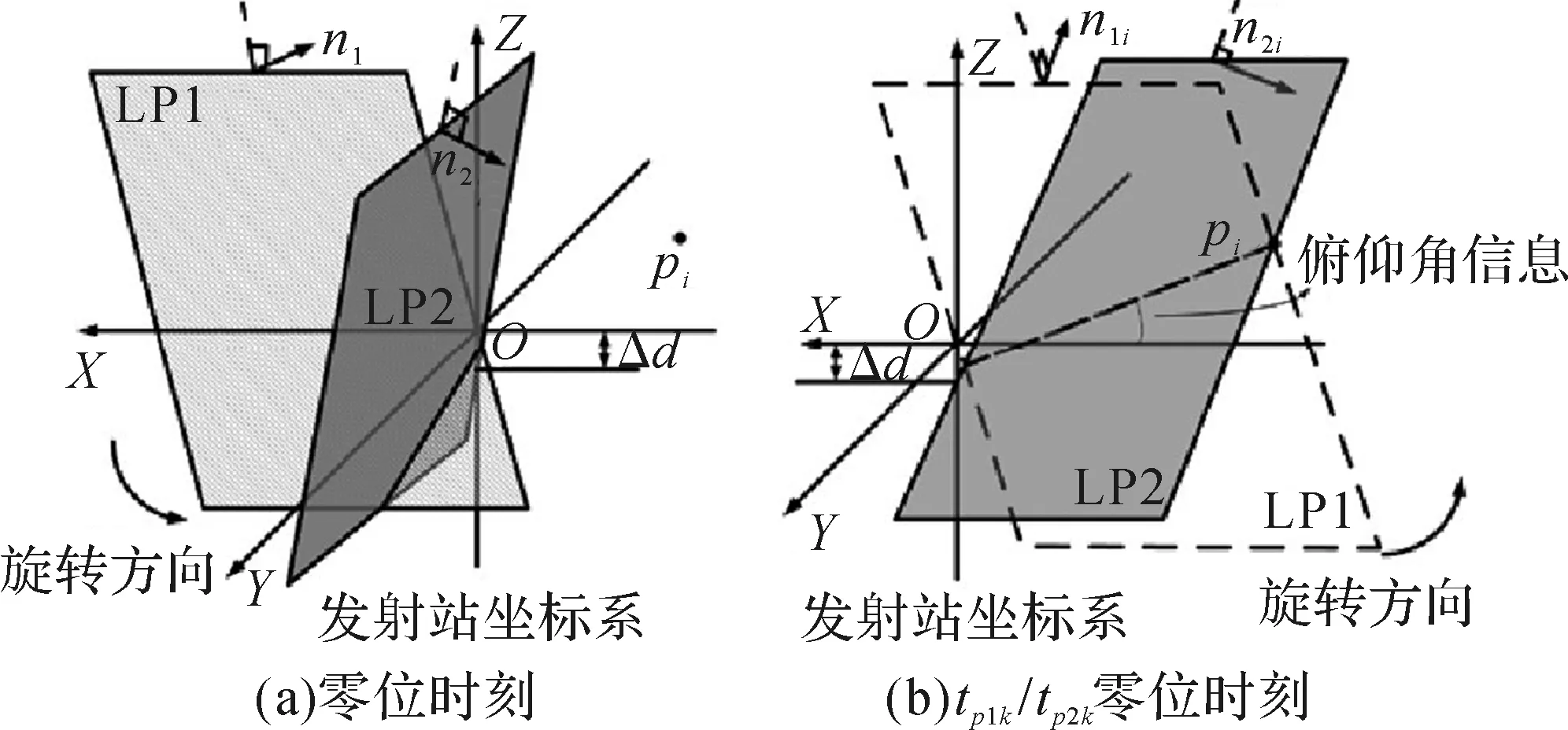
图4 待测点位置坐标的确定Fig.4 Determination of coordinates of point to be measured
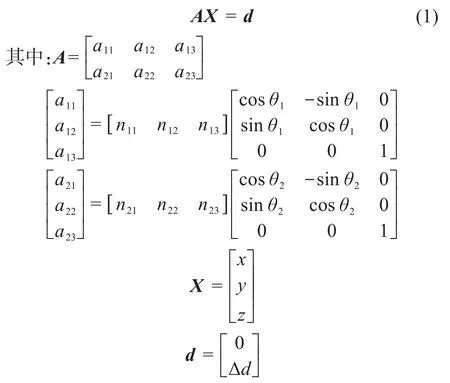
式中:θ1为LP1的水平角,θ2为LP2的水平角;(x y z)为待测点pi的坐标。
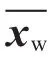

1.3 车体中心坐标提取算法
用IGPS引导AGV时,将发射站空间坐标系OXYZ转换成平面坐标系O-XIYI。AGV运行时,选取厂房二维平面坐标系作为车体坐标系O-XwYw,并设AGV在全局坐标系下的位姿Q=(x' y' θ')。发射站坐标系O-XIYI与车体坐标系O-XwYw的关系如图5所示。通过旋转角度α,可以将接收器J在发射站坐标系下的坐标(xJyJθJ)转换为车体坐标系下的坐标(xgygθg)。
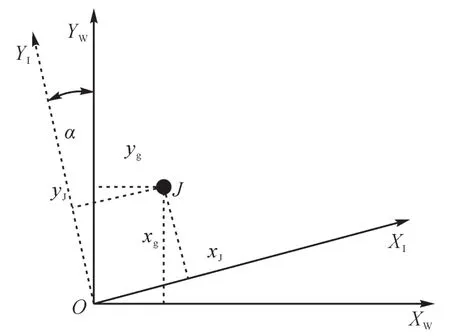
图5 发射站坐标系与车体坐标系的关系Fig.5 Relationship between transmitting station coordinate system and car body coordinate system
因此接收器J的坐标转换为:
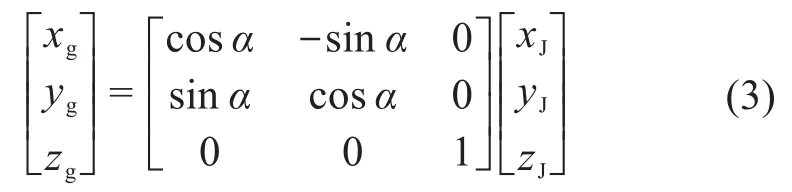
根据接收器在AGV的安装位置可以得出,车体中心坐标(x' y' θ')为:
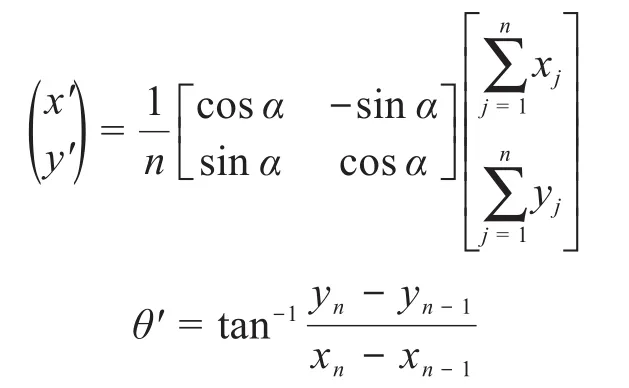
式中:xj为第j个接收器传输的有效的实际X坐标值,yj为第j个接收器传输的有效的实际Y坐标值;n为有效对接收器数。
1.4 AGV运动学模型
全向移动AGV在平面上有3个自由度,灵活度及运动精度较高[10]。其运动学模型如图6所示。
AGV的运动学方程为[10]:
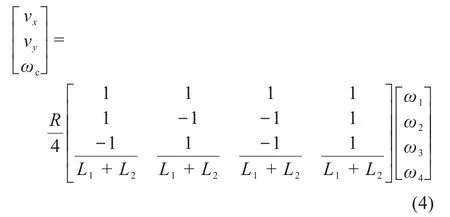
式中:vx、vy分别为AGV在X和Y方向的速度,mm/s;ωc为AGV的旋转角速度,rad/s;ω1、ω2、ω3、ω4分别为AGV4个轮子的角速度,rad/s;R为AGV轮子半径,mm;L1为AGV前后轮子距离的一半,L2为AGV左右轮子距离的一半,mm。
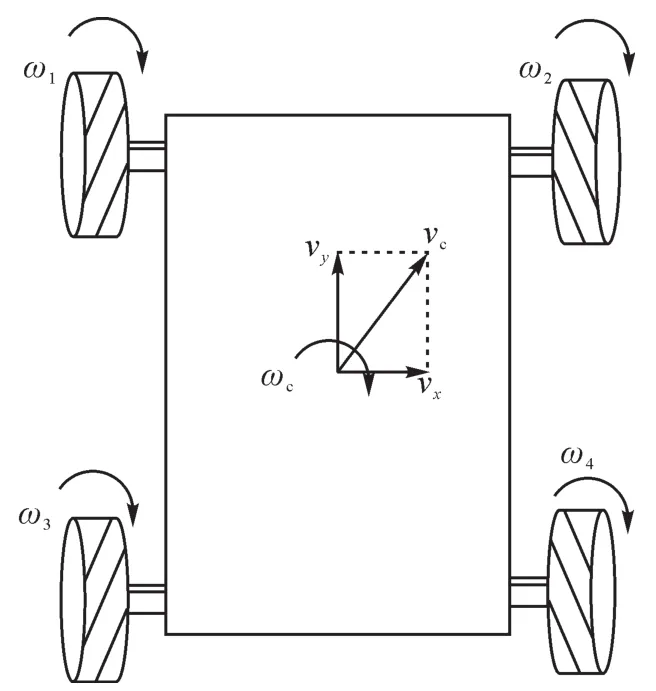
图6 全向移动AGV运动学模型Fig.6 Kinematics model of omnidirectional moving AGV
vc为vx与vy的合速度,可分解为偏航角φ(速度vc与车体中轴线的夹角)和速度值v。通过调控(φ,ωc,v)可以实现AGV在运动平面内的任意运动。其中φ与后续路径跟踪的距离偏差和沿目标路径的运行角度有关,ωc与目标路径的角度偏差有关。
AGV车体当前位姿与目标路径的偏差如图7所示,其中目标路径起点坐标为(xsys),目标点坐标为(xfyf)。AGV车体当前位姿与目标路径的偏差包括AGV车体中心当前坐标(x' y')与目标路径的偏移距离Δd'、AGV车体中心当前坐标(x' y')与目标坐标点(xfyf)的偏移距离Δl及AGV车体中心当前位姿角θ'与目标路径倾斜角θ的偏差角度Δθ'。
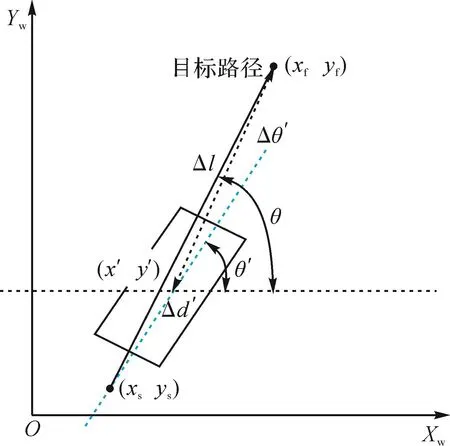
图7 AGV车体当前位姿与目标路径的偏差Fig.7 Deviation between current pose ofAGV and target path
根据接收器输出的位置信息,可以算得车体中心位姿。根据车体中心位姿和目标路径的偏差,来求取AGV运动的控制量:

式中:A=yf-ys,B=xf-xs,C=xfys-xsyf。
2 AGV模糊PI控制器的原理和设计
2.1 模糊PI控制器原理
IGPS接收器、导航控制器、驱动控制器之间采用串口通讯。IGPS接收器将获得的位置信息发送给导航控制器,导航控制器利用模糊PI算法计算出(φ,ωc,v)这3个控制量并发送给驱动控制器,实现对AGV运动的控制。
模糊PI控制是在传统PI控制的基础上引入模糊控制器,通过模糊控制器实现对PI控制器实际控制系数 kp、ki的调整[8,11-12,18]。模糊 PI控制原理如图 8所示。

图8 模糊PI控制的原理Fig.8 Principle of fuzzy PI control
2.2 AGV模糊控制器的设计
AGV模糊控制器是采用双输入双输出的二维模糊控制器[13-14],以车体偏航角φ控制Δd'的大小,旋转角速度ωc控制Δθ'的大小。因此采用位置控制器和旋转控制器对小车的平移和旋转进行独立控制。位置控制器输入量是AGV车体中心位姿与目标路径的距离偏差值Δd'和距离偏差率dt,输出量为比例系数Δkdp、Δkdi。旋转控制器输入量是AGV车体中心位姿与目标路径的角度偏差值Δθ'和角度偏差率θt,输出量为比例系数Δkθp,Δkθi。
首先将控制器输入量进行模糊化处理。从理论上讲,距离偏差值Δd'的取值范围为[- ∞,∞ ],但在实际情况中,由于受到客观条件的限制,当Δd'值过大时,现场环境无法满足AGV的运行需求。综合考虑AGV运行的灵敏性和延迟性,位置偏差Δd'的取值范围为[-300,+300]mm,角度偏差值Δθ'的取值范围为[-45°,45°]。将模糊论域分为7个等级,分别为NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)和PB(正大)[15-18]。
AGV模糊控制器的位置论域定义表如表1所示。
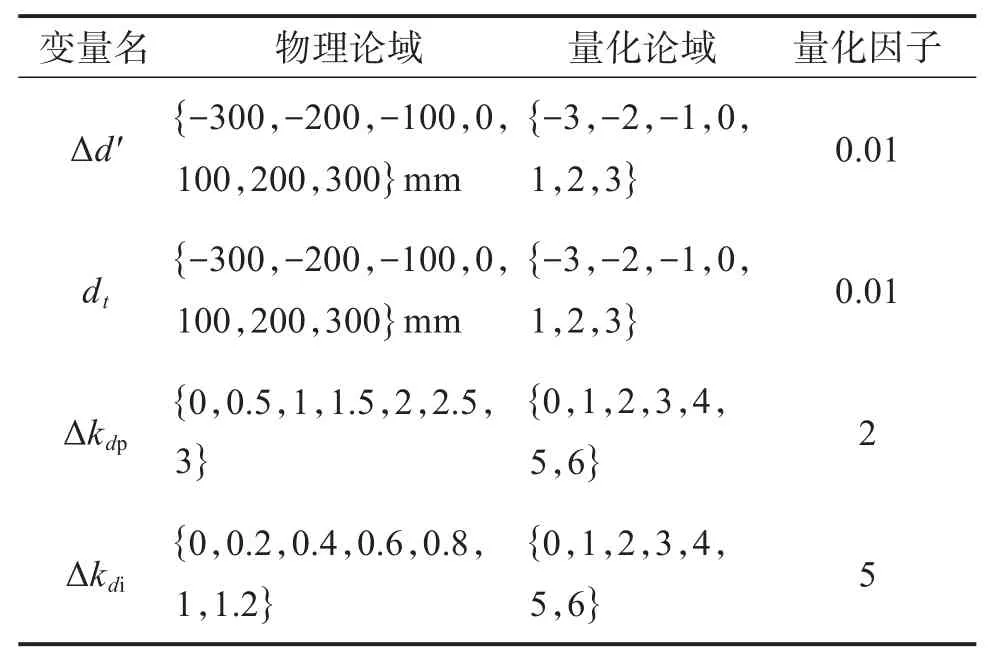
表1 AGV模糊控制器的位置论域定义表Table 1 Location domain definition table of AGV fuzzy controller
AGV模糊控制器的角度论域定义表如表2所示。
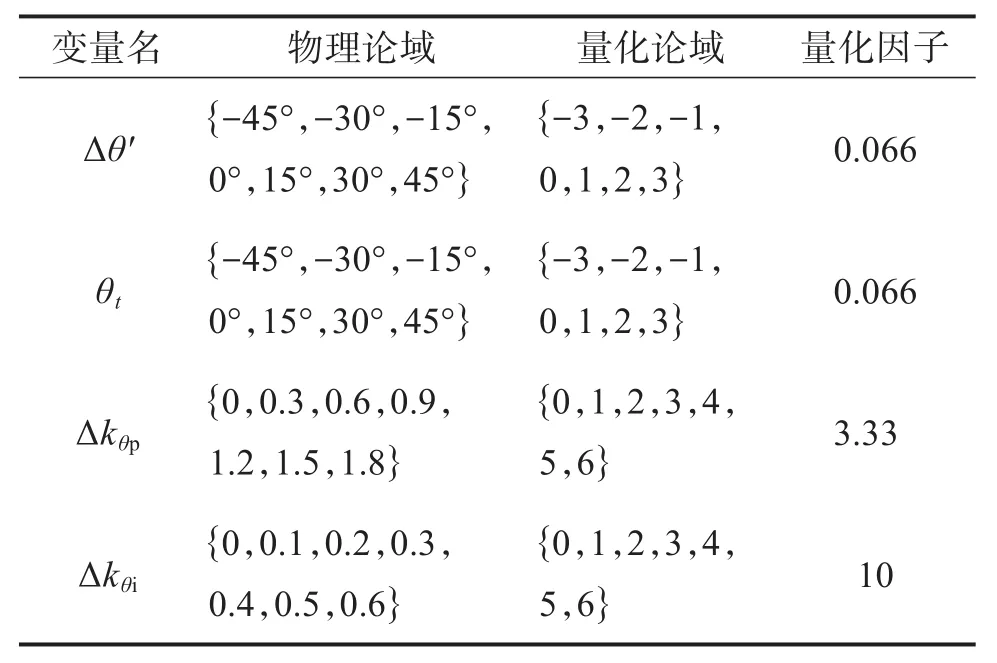
表2 AGV模糊控制器的角度论域定义表Table 2 Angle domain definition table of AGV fuzzy controller
获得论域后,需要选择合适的隶属度函数。本文采用三角型隶属度函数。与高斯型和正太分布型隶属度函数相比,三角型隶属度函数结构简单,不占用过多内存。根据AGV和路况信息,得到△kp和△ki的模糊推理规则表,如表3和表4所示。
为了获得较为准确的输出量,解模糊的清晰化方法采用加权平均法(即重心法)。该方法在工业控制中的应用效果较好。

式中:xm为隶属度值;μ(m)为输出模糊变量;s为加权平均判决结果。

表3 Δkp的模糊推理规则表Table 3 The fuzzy inference rule table ofΔkp
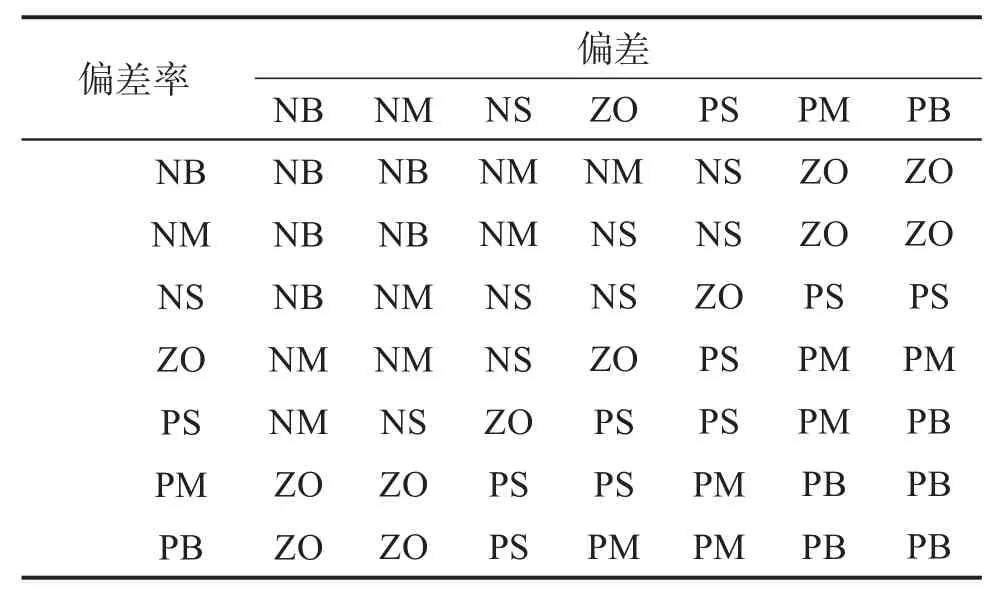
表4 Δki的模糊推理规则表Table 4 The fuzzy inference rule table ofΔki
由加权平均法得到的判决结果,还须乘以一个输出比例因子,才能满足控制要求,从而求得最终的输出量。

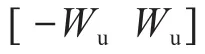
2.3 PI控制设计
PI控制是将设定值与实际输出值进行比较构成控制偏差,并将偏差的比例和积分通过线性组合构成控制量,对被控对象进行控制。
PI控制器采用经典PI增量式控制,其表达式如下:

式中:kp'、ki'为PI控制器初始参数;Δkp、Δki为模糊控制器的输出参数。
3 AGV导航控制仿真和试验
3.1 仿真分析
通过MATLAB的Simulink组件建立AGV导航模糊PI控制仿真模型,如图9所示。
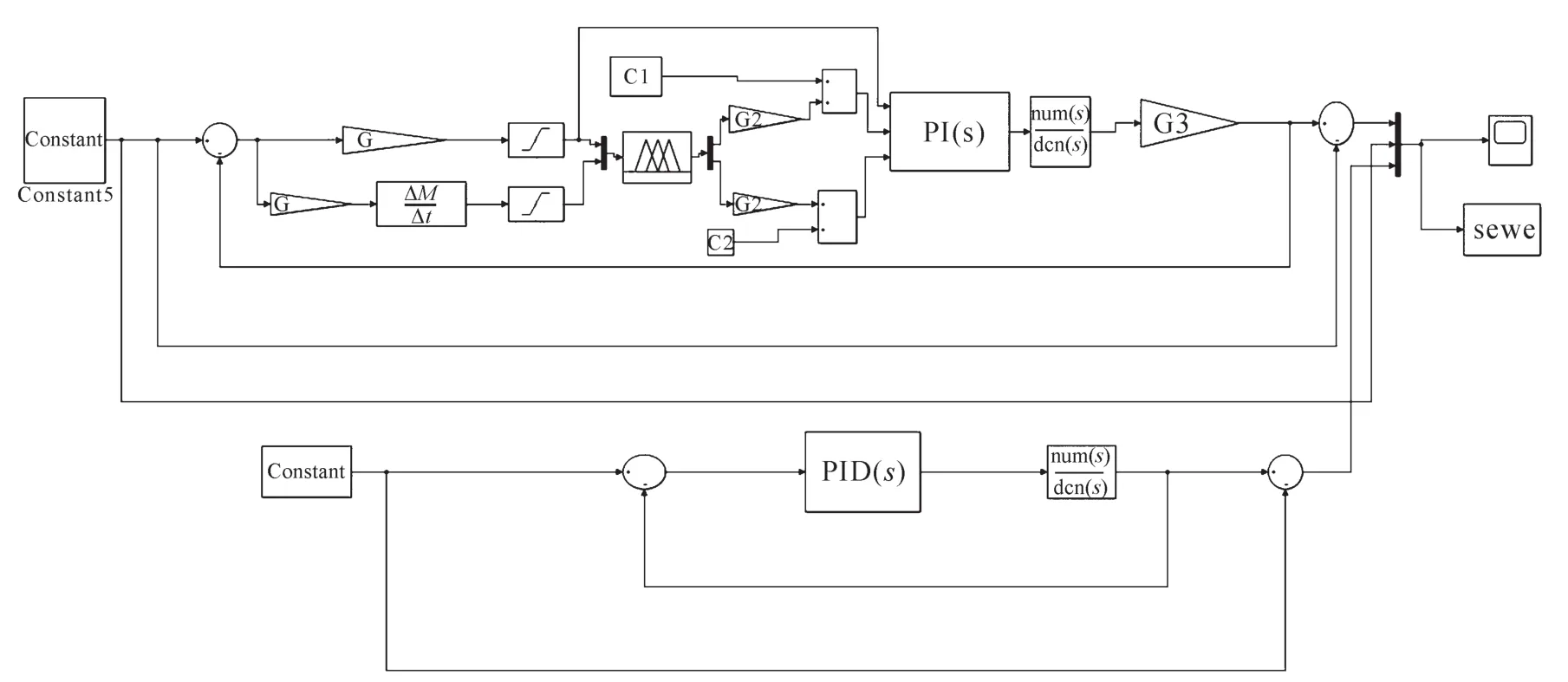
图9 AGV导航模糊PI控制仿真模型Fig.9 Simulation model of fuzzy PI control of AGV navigation
在MATLAB的Fuzzy Logic Controller中建立AGV导航模糊控制器,如图10所示。

图10 AGV导航模糊控制器Fig.10 Fuzzy controller of AGV navigation
对AGV导航模糊PI控制和传统PI控制进行仿真。为了检测在最大偏差下对AGV的控制情况,设置初始值输入分别为最大角度偏差45°和-45°以及最大距离偏差300和-300 mm,其仿真结果对比如图11所示。

图11 AGV导航模糊PI控制和传统PI控制的仿真结果对比Fig.11 Comparison of simulation results of fuzzy PI control and traditional PI control of AGV navigation
从图11可知,模糊PI控制和传统PI控制均可以使AGV在较大的角度偏差和距离偏差下调整到平衡状态,但模糊PI控制的速度和幅度均优于传统PI控制。可见,采用本文设计的模糊PI控制器可以显著提高AGV的纠偏能力和反应速度。
3.2 试验验证
笔者自主研发的基于IGPS的AGV试验平台如图12所示。

图12 基于IGPS的AGV试验平台Fig.12 AGV test platform based on IGPS
试验环境为工厂的地坪漆地面,采用激光跟踪仪进行位置检测。定位点的位置坐标为(-2307.877,1179.287,-677.001)mm,AGV连续在该点停靠200次。实际测得的AGV的定位位置与定位点位置的偏差如图13所示,可以看出定位距离偏差在-0.2~0.2 mm以内。
4 结论
本文提出了一种由IGPS导引的全向AGV定位方法,通过模糊PI闭环控制实现AGV定位控制。首先,实时获取IGPS接收器当前的位置坐标,并计算车体中心位姿和AGV车体中心与目标路径的偏差量,然后将偏差量作为输入量,利用模糊PI控制生成控制量,实现AGV的定位和导航。试验结果表明,基于IGPS和麦克纳姆轮的AGV定位方法,定位精度可达到±0.2mm,实现AGV的高精度定位。
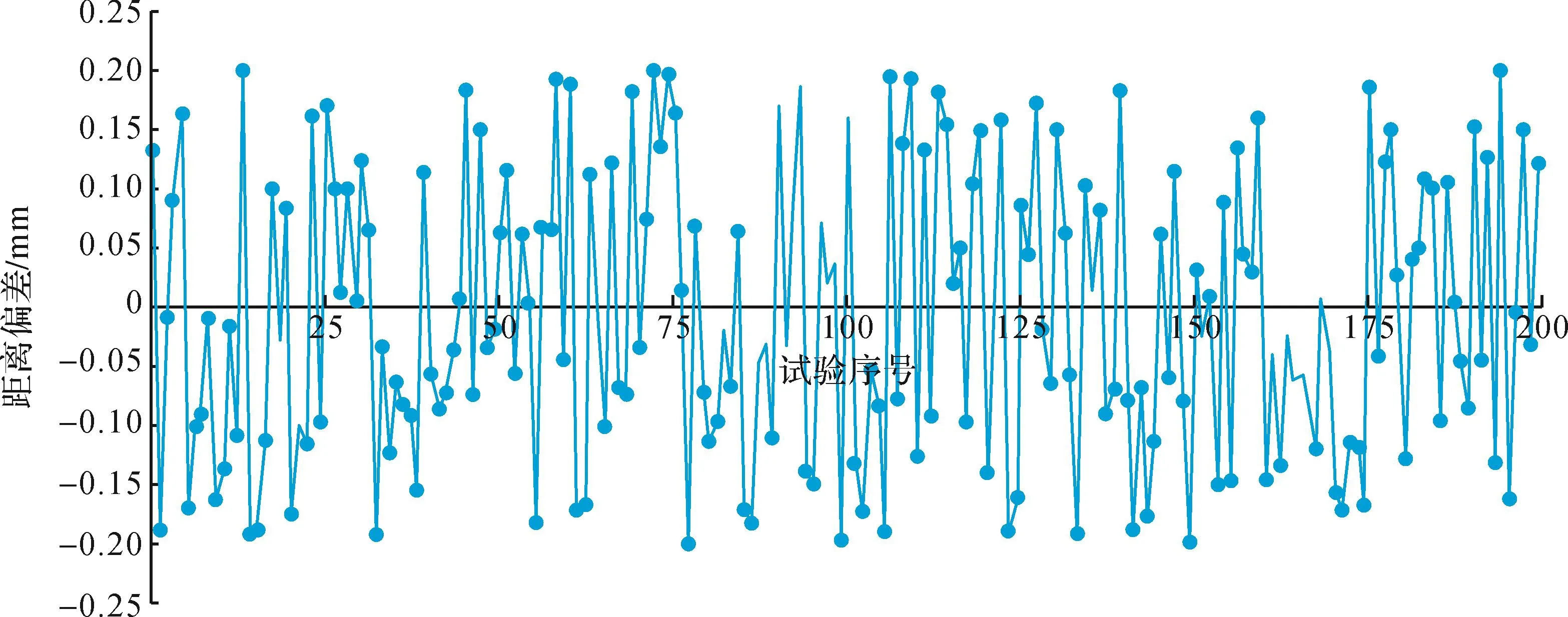
图13 AGV定位偏差Fig.13 AGV positioning deviation

