非均匀外挤压载下套管挤毁界限的仿真研究

李增亮，杜明超，李昆鹏，张 峰，张瑞霞

(1.中国石油大学(华东)机电工程学院，山东 青岛 266580；2.胜利油田石油工程技术研究院，山东 东营 257000)

1 引言

目前，由于油田开发已进入中后期，深埋井下的套管经过长时间的服役，已逐渐出现不同程度、类型的损坏。虽然各油气开发生产单位普遍认识到套损井治理在恢复老油田稳产基础和提高老油田综合经济效益方面的作用和意义，但目前套损井治理工作仍然零散运行，没有形成系统化和规模化，套损井逐年增加的趋势未能得到有效控制[1]。非均匀外挤压力是致使套管损伤的一个重要因素，通过开展非均匀外挤压力作用下套管的挤压行为和挤毁界限的研究，明确套管所承受挤压变形的能力，能够有效的降低修井成本、提高油井采油量。近年来许多专家学者对此进行了相关研究，李子丰等人[2]研究表明如果地层不具有蠕变性，地应力不会作用在套管上；如果地层具有蠕变性，且持续时间比较长时，套管所受的外挤载荷为地层的上覆岩层压力。但是随着油井的使用年限增加，井壁周围的疏松地层难免会发生坍塌、掏空等现象，从而使套管更易承受非均匀外挤载荷的影响。房军等人[3]分析发现随地应力非均匀程度的增加，套管形变经历了由两向挤压-挤压到两向拉伸-挤压组合方式的转变；夏雪梅等人[4]对承受单向外挤载荷的承载能力及其变形损坏进行了仿真研究；蔡正敏等人[5]对非均匀地应力下具有初始椭圆度的套管强度进行了分析。但是这些研究都未明确非均匀外挤压力及外载不均匀度与套管挤毁界限的关系。为此，笔者就非均匀外挤压力作用下套管的挤毁界限进行详细的分析与阐述。

2 弹塑性有限元模型建立

根据套管的实际变形情况，做出如下假设：①套管的初始椭圆度为零(即套管完好无损毁)；②水泥环、套管为均匀壁厚圆筒，且与井眼中心同心；③软地层、水泥环、套管均为各向同性材料；④套管和水泥的接触边界为完全接触[6]。

套管一般下入几千米深的地层内，由于岩层一般较厚，根据厚壁圆筒理论，将此问题处理成平面应变问题加以分析，因此依照上述假设建立分析模型，在套管变形井段取某一横截面进行套管挤压变形研究。

水泥环和岩层材料的本构关系均采用Drucker-Prager弹塑性本构模型。D-P本构模型是理想弹塑性模型，它综合了胡克定律和Coulomb破坏准则，并且采用更适用于数值计算的圆锥形屈服面函数。其中涉及到5个参数，即控制弹性行为的弹性模量和泊松比，以及控制塑性行为的粘聚力、内摩擦角和膨胀角。膨胀角是用来衡量体积膨胀大小的标度，在岩石工程中，一般密实的砂土和超强固结土在发生剪切作用的时候由于颗粒的重新排列会发生体积膨胀，而一般的岩石或者正常固结的土体，只发生剪缩[7]。因此在本文中，将膨胀角设置为0°比较符合实际工况。

套管——水泥环——地层整体有限元计算模型如图1所示，模型整体采用Plane82单元，套管与水泥环、水泥环与地层之间分别选用TARGE169单元和CONTA172单元来建立接触，保证力传递的连续性。根据岩石力学和弹塑性力学理论，不考虑套管所承受的内压，在平面无限远受Y方向压力为σh，X方向压力为σH，当地层边界超过井眼半径的5～6倍以后，对井周应力的影响很小，可忽略不计，所以本模型中地层宽度取为井眼直径的20倍[8]，在保证求解精度的前提下，减少有限元计算时的节点和单元总数，能够明显提高计算效率[9]，此外，考虑到模型的对称性，取1/4进行分析，并施加对称约束。套管常用的钢级及其相应的材料参数、水泥环参数及地层参数均来源于油田现场提供的生产数据和试验数据，研究中选取钢级为N80的5.5in×7.72mm、5.5in×9.17mm、7in×9.19mm和7in×12.65mm套管进行仿真分析。具体的套管、水泥环、地层的力学参数如表1所示。

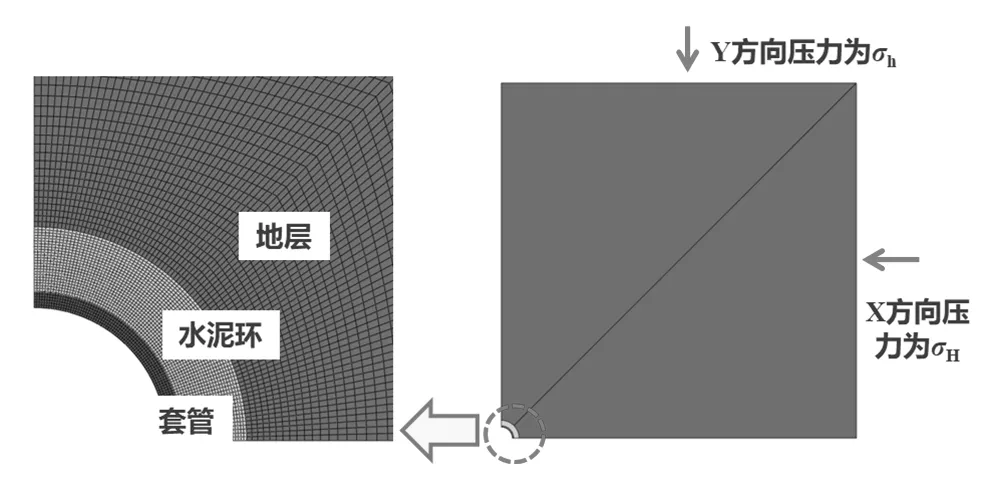
图1 套管非均匀受载有限元模型

表1 套管、水泥环和地层的力学参数

3 结果及分析

本文主要以钢级为N80，外径为139.7mm壁厚为7.72mm的套管的仿真求解结果为例进行详尽的分析与说明。

3.1 5.5in×7.72mm套管的挤毁界限研究

为了研究套管在非均匀外挤压力作用下的缩径变形规律，分析中选取不同大小的σH和σh的进行配比组合，但始终保证σH>σh。在计算过程中，将套管模型的最大变形量定义为在该外载情况下套管的最大缩颈，当出现导致数值分析计算结果发散的几何大变形时，则认为套管彻底损坏，同时将前一外载组合作用下套管的最大缩颈定义为套管在该外载情况下的挤毁界限。当Y方向挤压力σh大于75MPa或小于25MPa时，其数值分析结果和75MPa及25MPa相差不大，因此选取25,35,45,55,65,75MPa作为Y方向挤压力σh进行具体分析。不同Y方向挤压力所对应的X方向挤压力取到极限时套管最大缩颈如表2所示。

表2表明，外径13.9mm壁厚为7.72mm的套管在Y方向挤压力为25MPa，X方向挤压力135MPa时，其挤毁界限为11.85mm；但当Y方向挤压力为75MPa，X方向挤压力384MPa时，其挤毁界限为66.6mm。通过对比数据可以发现，套管在地层压力作用下的挤毁极限并不是一个定值，而是随着外载的不同发生改变。

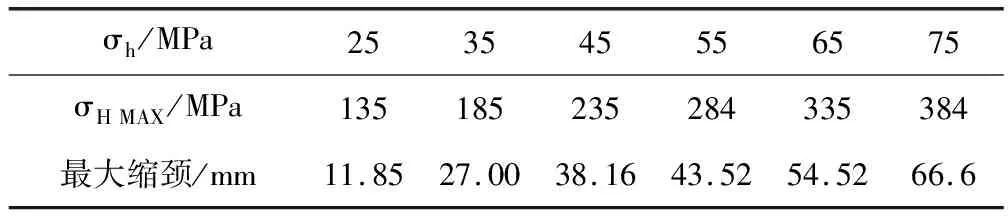
表2 X方向挤压力取到极限时套管最大缩颈

为了明确在不同外载条件下套管的挤毁界限，将Y方向挤压力作为自变量，套管的挤毁界限作为因变量进行数值拟合，得到如下公式：

y =-5.729×10-6x4+ 0.001698 x3-0.1678 x2+7.659 x-99.19

(1)

其中，x-Y方向挤压力/MPa；y-套管挤毁界限/mm。

该公式的SSE(误差平方和)为3.395，R-Square(确定系数，越接近1，表明方程的变量对y的解释能力越强，模型对数据的拟合也较好)为0.9982。通过测量Y方向(变形长轴方向)的外载压力，代入上述公式，便可求得在该压力下套管的挤毁界限。

笔者认为，套管的挤毁极限之所以会随着外载的不同而发生变化，是因为X方向和Y方向的挤压力相差过大所致。为更加明确的阐述套管双侧变形损坏的机理，同时减小上述方程的误差，引入外载不均匀度进行分析。

外载不均匀度定义为x方向外挤压力于y方向外挤压力的比值(以下均称为不均匀度)。

套管达到挤毁界限时所对应的极限不均匀度如表3所示。

表3 套管挤毁界限所对应的极限不均匀度

从上表中可以发现，外径为139.7mm壁厚为7.72mm的套管在外载不均匀度为5.12～5.4的范围内时会发生挤毁，且该套管所能承受的极限不均匀度随外载的增加而降低。

将Y方向挤压力和该压力作用下的极限不均匀度进行数值拟合，得到曲线图2所示:

图2 Y方向挤压力-极限不均匀度拟合曲线

方程为：

b=-8.333×10-8a4+ 1.5×10-5a3-0.0008292 a2+ 0.007554 a + 5.52

(2)

式中，a-Y方向挤压力/MPa，b-极限不均匀度；

误差平方和SSE:0.0001286；确定系数R-Square:0.9977。

再将极限不均匀度和挤毁界限进行数值拟合，得到如下曲线：

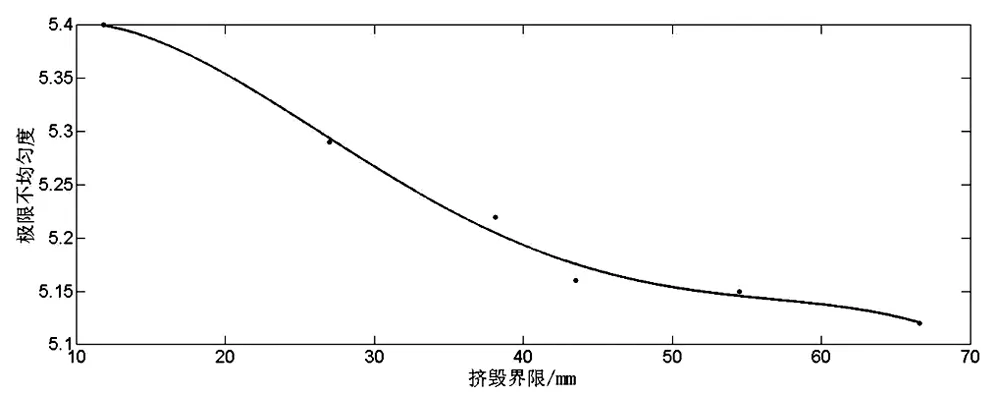
图3 套管最大缩颈-极限不均匀度拟合曲线

方程为：

b=-1.313×10-7c4+2.185×10-5c3-0.001177 c2+0.01719 c+5.327

(3)

式中，c-套管挤毁界限/mm；

误差平方和SSE:0.0005107；确定系数R-square:0.9908。

将测得Y方向挤压力代入公式(2)求得该压力作用下的极限不均匀度，然后用公式(3)求得该压力作用下的挤毁界限。公式(2)和(3)的误差平方和分别为0.0001286、0.0005107，和公式(1)的SSE相比小很多，因此通过加入不均匀度来求解套管挤毁极限缩颈可以很好的减小拟合误差。

3.2 5.5in×7.72mm套管的最佳修井尺寸

应力-应变曲线的形状反应材料在外力作用下发生的弹性、屈服、塑性、断裂等各种形变的阶段。套管在非均匀外挤压力的挤压下同样会发生类似的形变过程，即由弹性阶段到屈服阶段，再到塑性阶段，最后发生挤毁压溃现象。现将数值模拟得到的套管缩颈量和套管内部的最大应力进行曲线拟合，得到5.5in×7.72mm套管在不同外载作用下的应力-应变曲线。图4为Y方向挤压力25MPa套管应力-应变曲线。

图4 Y方向挤压力25MPa套管应力-应变曲线

从图线中可以看出，缩颈量在0.45mm到1.3mm范围内时，曲线大部分为一条偏离纵轴的斜直线，表示套管内部应力与缩颈量成正比，服从虎克定律，套管进入弹性阶段。套管缩颈量在1.3～4mm时，图线变为一条具有小幅度波动的线段，此时应力几乎不增长，但是套管缩颈却迅速增加，套管进入屈服阶段。套管缩颈量在4 ～9mm时，图线为一条上弯曲线。这表明套管经过屈服阶段之后，又恢复了抵抗挤压变形的能力，如果要使其继续变形，必须增大外挤压力。当套管缩颈达到9mm时，套管内最大应力达到峰值，即套管的抗压强度846MPa。随后套管缩颈在9～11.85mm时，套管内部应力集中处发生应力释放，如图5、图6所示，Y方向挤压力25MPa、X方向挤压力130MPa时套管内的最大应力为846MPa，Y方向挤压力25MPa、X方向挤压力135MPa时套管最大应力为825MPa。说明此时套管局部已经发生破坏，缩颈量增加，等效应力逐渐降低，最后发生挤毁。

图5 Y方向挤压力25MPa、X方向挤压力130MPa套管应力云图

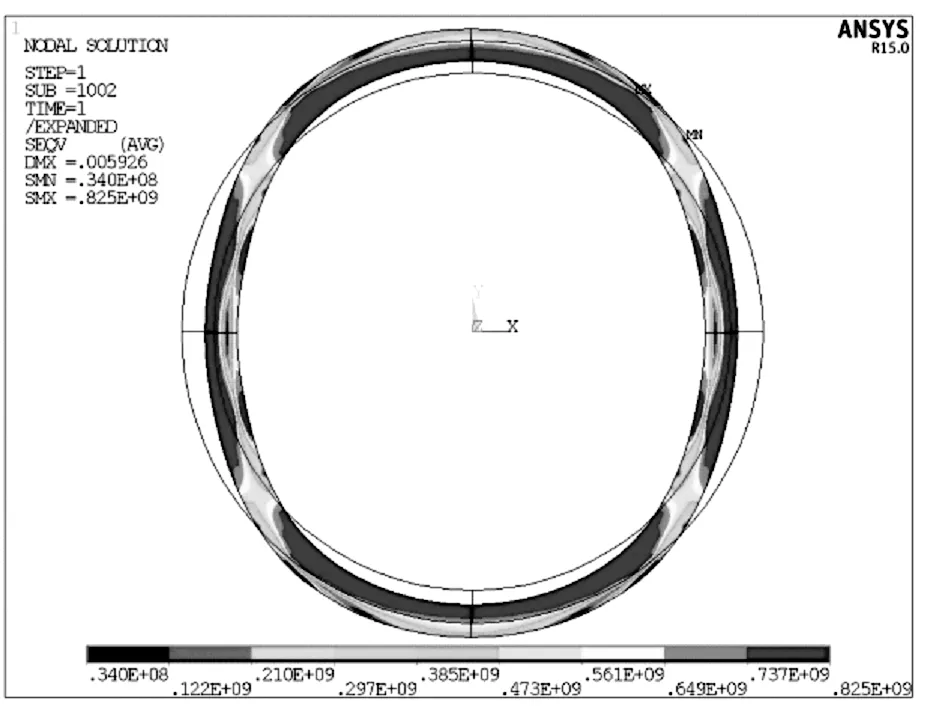
图6 Y方向挤压力25MPa、X方向挤压力135MPa套管应力云图

当Y方向挤压力≥45MPa时，随着外载的增大，套管进入弹性阶段的时间逐渐减小，且当缩颈达到9mm时，套管内的最大应力并未达到整个过程的最大值。然而在缩颈量超过该临界点之后，套管内的最大应力并不随着最大缩颈的增大而减小，而是发生了不规则震荡。随着Y方向挤压力的增大，震荡的幅度和频率也增大。图7为Y方向挤压力55MPa套管应力-应变曲线。

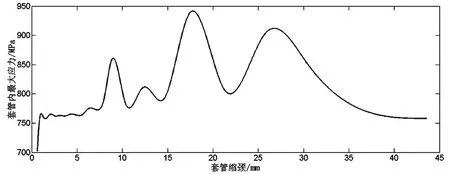
图7 Y方向挤压力55MPa套管应力-应变曲线

综上所述，5.5in×7.72mm套管的变形量为9mm时是一个临界点。在这个临界点之前，套管仍然具有抵抗变形的能力，但变形量超过9mm，套管内部或出现应力释放现象，或出现套管内应力随形变量增大而不规则震荡现象，两种现象都可能表明套管已经发生局部破坏。该种条件下即使修复其抵抗二次挤压的能力也大大降低。因此，将9mm定义为5.5in×7.72mm套管在非均匀外挤压力力作用下的最佳修井尺寸。

为得到套管缩颈量和不均匀度之间的关系，将不同外挤压力挤压下的套管缩颈和其所对应的不均匀度拟合曲线，如图8所示。

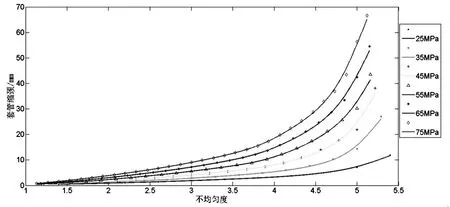
图8 5.5in×7.72mm套管不均匀度-套管缩颈拟合曲线

该曲线表明，外载不均匀度小于3.5时，最大缩颈随不均匀度的增大而近乎线性增大，当不均匀度大于3.5时，最大缩颈随不均匀度的增大呈现类似抛物线增大。应力-应变曲线发生震荡最剧烈的位置是在由线性向抛物线转换的阶段，即3.5～4.5范围内。

4 结论

(1)通过对比X方向外挤压力取极限值时套管的最大缩颈可知，套管的挤毁界限并不为定值，而是随外部载荷的增加而增大，并给出了表述两者关系的拟合方程。

(2)当Y方向挤压力大于25MPa时，套管的挤毁界限之所以会随着外载的不同而改变，是因为X方向和Y方向的外挤压力相差过大所致。外径为139.7mm壁厚为7.72mm的套管在Y方向大于等于25MPa的情况下，在外载不均匀度达到5.12～5.4的范围内时，便会发生挤毁，且该套管承受的极限不均匀度随外载的增加而降低。

(3).在求解5.5in×7.72mm套管在非均匀外挤压力的挤压下的挤毁界限时，通过引入外载不均匀度作为变量，能够很好的减小拟合误差，增大求解精度。

(4).从套管受不均匀外挤压力挤压的角度分析，将缩颈9mm定义为5.5in×7.72mm套管的最佳修井尺寸。不均匀度小于3.5时，套管缩颈量随不均匀度的增大而近乎线性增大，当不均匀度大于3.5时，套管缩颈量随不均匀度的增大进行类似抛物线增大。应力-应变曲线发生震荡最剧烈的位置是在由线性向抛物线转换的阶段。