基于模糊综合评价法的辅导员工作负荷评估研究

杜文玲,赵悦悦

(淮南师范学院 马克思主义学院，安徽 淮南 232038)

辅导员作为与大学生接触最多的教师，其工作琐碎而庞杂，需要时刻关注学生的生活与学习等各种情况，几乎需要全天候待命，事务性工作较多，工作时间过长，工作量大，因此会出现职业倦怠的现象。但目前尚无研究涉及对辅导员的工作负荷评估。模糊综合评价法以模糊数学为基础，按照隶属度理论，通过模糊数学对研究对象进行综合评价，具有系统性强和评价结果明确等特点。使用模糊综合评价法评估高校辅导员工作负荷情况，可为开展高校思政工作提供指导。

为深入分析辅导员工作负荷的影响因素，需要构建辅导员工作负荷评估指标体系，以期为后续辅导员工作负荷评估奠定基础。

一、辅导员工作负荷评估指标体系的构建

通过问卷调查法统计安徽某高校60位大学辅导员工作负荷情况，根据调查结果，在前人研究成果的基础上，构建高校辅导员工作负荷评价指标体系(图1)[1]。评价指标体系由4个一级指标及8个二级指标组成。一级指标分别为工作压力、环境因素、思政教育以及绩效考核因素，二级指标包括工作时间、工作内容、职业环境、文化环境、教学工作、科研工作、教学绩效和职称评定。

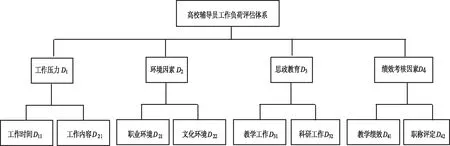
图1 高校辅导员工作负荷评估指标体系

由于辅导员工作负荷也是一种非线性问题，因此该文以构建的评估指标体系为基础，采用模糊综合评价法对辅导员工作负荷进行评估。

二、辅导员工作负荷模糊综合评估研究

在构建高校辅导员工作负荷评估指标体系的基础上，通过确定指标权重向量、一致性检验、确定评估等级论域以及模糊矩阵，来实现辅导员工作负荷模糊综合评估。

(一)确定指标权重向量

以高校辅导员工作负荷评价指标体系为基础，使用重要性标度对一级指标中各因素实行两两比较，构建判断矩阵：D=(dij)p*p，该判断矩阵需要满足以下3个关系才能保证每两个判断矩阵之间完全具备一致性[2]：

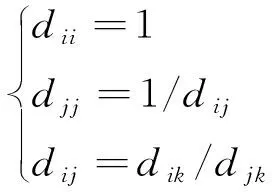
(1)

使用和积法计算判断矩阵的最大特征向量和与其对应的最大特征值，最后归一化处理判断矩阵[3]。

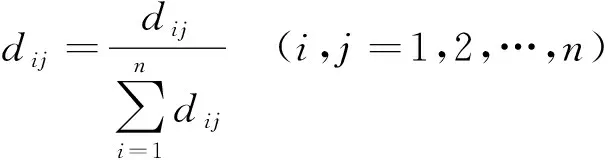
(2)

按行相加判断矩阵

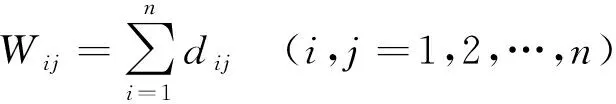
(3)

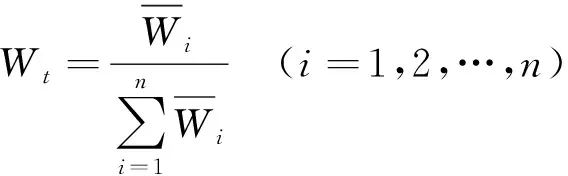
(4)

求得特征向量近似解W=(W1,W2,…，Wn)t。根据判断矩阵特征向量求得最大特征值[4]：

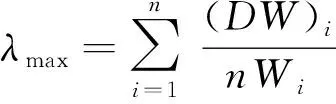
(5)

在以上分析基础上，需要对判断矩阵进行一致性检验。

(二)一致性检验

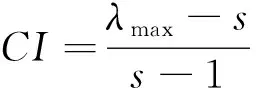
(三)评估等级论域确定

在判断矩阵通过一致性检验后，需要确定评估等级论域。设置辅导员工作负荷评价等级论域：X=(x1,x2,…xn)，其中x1,x2,…,xn代表评价标准。确定论域能够保证一个模糊评价向量的存在性，根据该模糊向量能够表达各评价指标评价等级隶属度信息，由此能够将评价的模糊性体现出来。根据辅导员工作负荷实际情况确定评价集[6]：评价结果分为无负荷、轻微负荷、中度负荷与重度负荷，评价集则有：X={x1(无负荷)，x2(轻微负荷)，x3(中度负荷)，x4(重度负荷)}。在确定辅导员工作负荷评价等级论域后，需要构建模糊矩阵。

(四)模糊矩阵的确定

根据评估等级论域确定模糊矩阵，以实现辅导员工作负荷评估，模糊判断矩阵为：

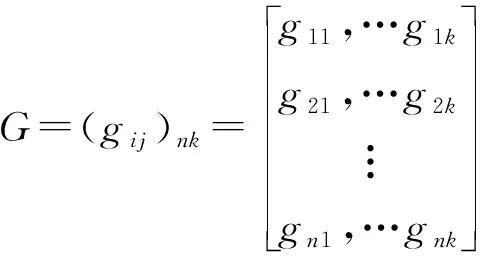
(6)

在模糊判断矩阵中，指标gij(i=1,2,…n;j=1,2,…k)表示各指标对于模糊判断矩阵的隶属度。

确定模糊矩阵的具体步骤如下：第一步，单因素评价。邀请专家成立专家组，专家根据评价集对各指标作出评价。第二步，对评价结果进行整理。计算出各评价指标与评价集之间的隶属度。如果有pi1个专家认为二级指标D11可以被评为无负荷，pi2个专家评价为轻微负荷，pi3个专家评价为中度负荷，pi4个专家评价为重度负荷，那么二级指标D11评价隶属度表示为：

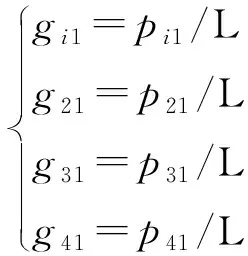
(7)

其中，L表示参加评价的专家人数。根据二级指标评价隶属度计算结果，获取二级指标模糊矩阵Gnk与一级指标模糊矩阵Gn。以构建的模糊矩阵为基础，实现辅导员工作负荷模糊综合评估。

(五)模糊综合评估

根据模糊矩阵对辅导员工作负荷进行模糊综合评估。邀请专家对辅导员工作负荷评价指标进行深入研究，在这些指标中，一部分可以通过直接定性分析得出评价等级，但部分指标仍然需要定量计算，根据计算结果判定评价等级。综合评价一级指标为Dn，Fn=H*Gn，H表示一级指标权重集；综合评价二级指标为Dnk，Fnk=Hnk*Gnk，Hnk表示与各指标对应的权重集。

根据以上模糊综合评价可得到对辅导员工作负荷评估值，工作负荷水平常用能量代谢率(RMR)和其他生理指标表示。表1为负荷评估标准，将计算得到的评价值与表1对比，判断高校辅导员的工作负荷情况。

表1 负荷评估标准(RMR)

为了验证该文提出的基于模糊综合评价法的辅导员工作负荷评估方法的有效性，需要进行实验验证，具体验证过程如下。

三、辅导员工作负荷评估研究的实验分析

为了验证基于模糊综合评价法的辅导员工作负荷评估方法的实际应用效果，进行实验测试，测试内容为实力分析及准确率测评。

(一)实例分析

对安徽某高校60位大学辅导员工作负荷情况进行评估，评价内容为思想政治教育及监督学生日常工作与学习情况。

1.确认指标权重

需要首先确认负荷评估指标权重，以得到辅导员工作负荷评估结果。按照重要性指标，使用德尔菲法构建判断矩阵，由此获取权重向量及最大特征值，并对其实行一致性检验。权重向量分别为A=(0.288,0.125,0.379,0.252),CR=0.069;A1=(0.444,0.778),CR=0;A2=(0.682,0.297),CR=0；A3=(0.41，0.41),CR=0.036;A4=(0.86,0.36),CR=0。最大特征值λmax分别为3,4,3.16,2,4.285；平均随机一致性指标CR均小于0.1，一致性良好。以确定的指标权重为基础，利用模糊矩阵进行辅导员工作负荷模糊综合评估。

2.确立模糊矩阵

根据指标权重确定模糊矩阵，并对这60位辅导员的工作负荷情况进行评估。评价标准分为无负荷、轻微负荷、中度负荷以及重度负荷，对工作负荷实行评价得到原始数据(表2)。

表2 指标评价结果

根据表2和指标权重向量评价二级指标：

根据该评价结果可知，仅6%的辅导员认为工作时间过长没有产生负荷，13%的辅导员觉得工作时间过长会产生轻微负荷，33%的辅导员认为工作时间过长会导致中度负荷，52%的辅导员认为工作时间过长会造成重度负荷。根据上文中的评价集，将评估等价转换为分数：

U1=F1*ZR=(0.06,0.13,0.33,0.52)*(588)R=7.69。

其中，ZR表示等价转换系数。

按照以上方法依次可得到其它指标的评价结果与分数：F2=(0.31,0.35,0.25,0.13)，U2=5.47；

F3=(0.15.0.23,0.29,0.37)，U3=6.83；F4=(0.07,0.1,0.27,0.59)，U4=7.83；

U1=F*ZR=(0.12，0.19，0.18，0.43)*(3587)R=6.45。

依据计算得出的负荷评估结果可知，辅导员处于中度负荷，主要负荷来自教学工作和科研工作。为进一步验证该文所提出的高校辅导员的工作负荷评估方法的有效性，需要进行评估准确率对比实验。

(二)准确率测评

为验证上述所得出的负荷评估结果准确性，采用模糊综合评价法、经济评价法和指标评价法对10位高校辅导员的工作负荷实行测评，测评结果见表3。可以看出，该文方法评估结果与辅导员工作的实际负荷情况最为接近，另两种评估方法与实际负荷评估结果具有一定差异，这说明该文方法比其他评估方法性能更好，同时证明该文方法具有良好的应用效果。

表3 负荷测评(RMR)

通过模糊综合评价法对高校辅导员工作负荷进行评估，探讨高校辅导员工作负荷情况与影响因素。通过实例分析，发现高校辅导员工作负荷属于中度负荷，对其工作和生活都有一定影响。实验分析证明模糊综合评价法的评估结果最接近实际，评估准确性较高，且经过评估后所制定调节计划可使其工作质量得到提高，证明该方法实用性较强。经过该文分析可知，当前辅导员工作负荷普遍较高，高校要根据实际情况适当减轻辅导员工作负担，如提升辅导员自身能力、探索辅导员工作改革创新策略、提倡“扁平化”管理和“信息化”办公以及制定相关的激励机制等，以期进一步提升辅导员的工作质量与效率，保证高校思政工作的顺利开展。