一般矩阵特征值的Wielandt-Hoffman型扰动上界

孔祥强

(菏泽学院 数学与统计学院，山东 菏泽 274015)

0 引 言

矩阵特征值扰动是矩阵扰动分析的重要分支.文献[1]研究了Hermite矩阵及可对称化矩阵特征值的扰动，改进了原有结果.文献[2]对可对角化矩阵加法和乘法的组合扰动进行了研究，推广了以往结果.文献[3]给出了正规矩阵对扰动的Wielandt-Hoffman型扰动界，推广了正规矩阵对的扰动结果.文献[4]讨论了用正单位线性映射得到两正规矩阵特征值之间的最大距离的下界问题，同时分析了与Hermite矩阵相关的扰动下界.文献[5]研究了广义鞍点矩阵和Hermite块三对角矩阵的结构化扰动，所给界限揭示了特征值关于不同块的扰动的敏感性.本文研究了一般矩阵特征值的扰动上界问题，利用矩阵的分解，得到一般矩阵特征值扰动的Wielandt-Hoffman型扰动上界，推广了一般矩阵特征值的扰动界.同时，分析了可对角化矩阵特征值的扰动，得到其扰动上界，且所得结论改进了以往结果.

1 预备知识

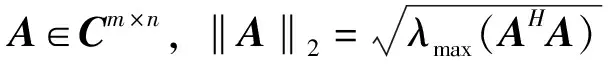
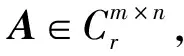
设A∈Cn×n，则存在酉阵U，使得UHAU=T，记T=M+Λ，M为严格上三角阵，Λ=diag(λ1,λ2,…,λn)，λ1,λ2,…,λn为A的n个特征值，称为A的Schur三角分解[9].

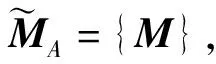
引理1[10]设A=(ajk)n×n，B=(bjk)n×n均是正规阵，Q∈Cn×n是Hermite正定阵，其特征值γ1≥γ3≥…≥γn，c是任意正数，则

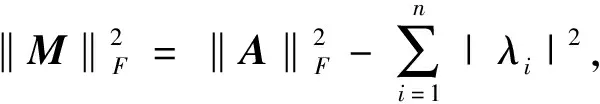
2 主要结果

定理1设A,B∈Cn×n，λ(A)={λi}，λ(B)={μi}，则存在1,2,…,n的某排列π使得

ΔF(A)+ΔF(B)).

证明由Schur三角分解，存在酉阵C，D，使得

A=CH(T1+M1)C,B=DH(T2+M2)D,

其中T1=diag(λ1,…,λn)，T2=diag(μ1,…,μn)，M1,M2均为上三角阵.

B-A=DHT2D+DHM2D-CHT1C-CHM1C.

由上式得

C(B-A)DH=

CDHT2+CDHM2-T1CDH-M1CDH,

D(B-A)CH=

T2DCH+M2DCH-DCHT1-DCHM1，

作CDH的奇异值分解CDH=VΣUH，Σ=diag(σ1,…,σn)，σ1≥…≥σn>0，U，V均为酉阵，则

ΣUHT2U-VHT1VΣ=VHC(B-A)DHU-

ΣUHM2U+VHM1VΣ,

(1)

UHT2UΣ-1-Σ-1VHT1V=UHD(B-A)CHV-

UHM2UΣ-1+Σ-1VHM1V.

(2)

令G=UHT2U，S=VHT1V，则G酉相似于T2，S酉相似于T1，故G,S均为正规阵，λ(G)=λ(B)，λ(S)=λ(A).

将G,S代入式(1)和式(2)得

ΣG-SΣ=VHC(B-A)DHU-ΣUHM2U+

VHM1VΣ,

GΣ-1-Σ-1S=UHD(B-A)CHV-UHM2UΣ-1+

Σ-1VHM1V,

则

‖ΣG-SΣ‖F≤‖C‖2‖B-A‖F‖D-1‖2+

‖Σ‖2‖M2‖F+‖M1‖F‖Σ‖2≤

‖C‖2‖B-A‖F‖D-1‖2+

‖C‖2‖D-1‖2‖M2‖F+

‖M1‖F‖C‖2‖D-1‖2=

‖C‖2‖D-1‖2(‖B-A‖F+

‖M2‖F+‖M1‖F),

(3)

‖GΣ-1-Σ-1S‖F≤

‖D‖2‖B-A‖F‖C-1‖2+

‖M2‖F‖D‖2‖C-1‖2+

‖D‖2‖C-1‖2‖M1‖F=

‖D‖2‖C-1‖2(‖B-A‖F+

‖M2‖F+‖M1‖F).

(4)

依引理 1，有

(5)

将式(3)，(4)代入式(5)得

‖M2‖F+‖M1‖F)2,

又c为任意正数，不妨令

则

A‖F+‖M2‖F+‖M1‖F).

(6)

依引理 2，有‖M1‖F=ΔF(A)，‖M2‖F=ΔF(B)；又C,D是酉阵，故K(C)=1，K(D)=1.

式(6)为

ΔF(A)+ΔF(B)).

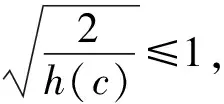
3)A为正规阵，B为任意阵，则

4)A为任意阵，B为正规阵，则

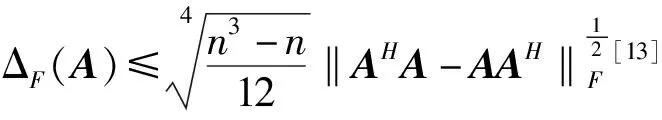
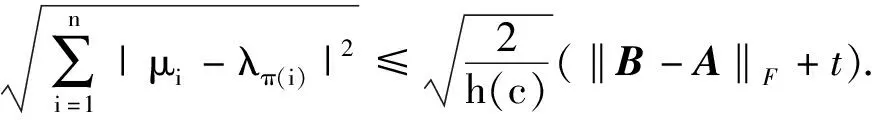
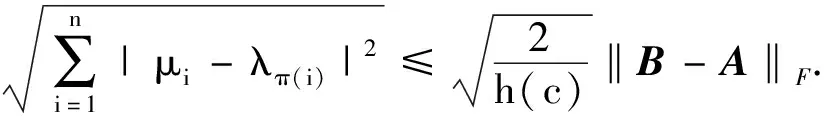
定理2设A,B均是可对角化矩阵，C,D为非奇异阵，A=CT1C-1，B=DT2D-1，T1=diag(λ1,…,λn)，T2=diag(μ1,…,μn)，λ(A)={λi}，λ(B)={μi}，非奇异阵Y∈Cn×n，则存在1,2,…,n的某排列π，使得

证明由A=CT1C-1，B=DT2D-1，C，D均非奇异，则

‖AY-YB‖F=

‖Y(D(D-1Y-1CT1-T2D-1Y-1C)C-1)Y‖F≥

T2D-1Y-1C‖F,

(7)

‖AY-YB‖F=

‖C(T1C-1YD-C-1YDT2)D-1‖F≥

(8)

作C-1YD的奇异值分解C-1YD=UΣVH，Σ=diag(σ1,…,σn)，σ1≥…≥σn>0，U,V均为酉阵.

令G=UHT1U，S=VHT2V，则G，S均为正规阵，λ(G)=λ(A)，λ(S)=λ(B).

将G,S代入式(7),(8)得

‖AY-YB‖F≥

T2VΣ-1UH‖F=

(9)

(10)

依引理 1，有

(11)

将式(9)，(10)代入式(11)，得

又c为任意正数，不妨令

则

‖G-S‖F≤

注21)若A,B均为可对称化矩阵，定理2的结论仍成立.由于

故定理 2 较文献[14]的结论3.2.6更强.

2)A,B均为正规阵，Y为单位阵，则

‖A-B‖F,

故定理2是Wielandt-Hoffman定理的推广.

3 算 例

考虑三阶可对角化矩阵

则存在非奇异阵

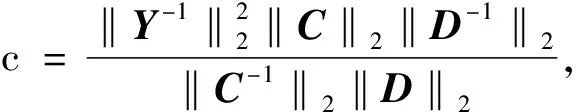
4 结 论

本文首先研究了一般矩阵特征值的扰动，利用矩阵的分解，得到Wielandt-Hoffman型绝对扰动上界，且所得结果推广了以往结论.其次，研究了可对角化阵特征值的扰动，所得结论适用于可对称化阵，且结论是Wielandt-Hoffman定理的推广.