光纤-薄壁结构应力传递有限元分析

张启威，张丽梅，韩文曼，王志强，郭 涛

(中北大学 仪器科学与动态测试教育部重点实验室，山西 太原030051)

0 引 言

薄壁结构被广泛应用于航天航空制造业等领域，但外界环境的改变容易对薄壁结构造成损伤，从而损坏结构体内的仪器设备，所以对薄壁结构的应力监测十分重要[1].传统的分立式传感技术已经无法实现对整个薄壁结构应力场的监测，而随着分布式传感技术的不断发展，光纤作为一种性能优良的分布式传感器得到了广泛的研究和应用.将光纤传感器应用在薄壁结构的应力监测中，能够实现应力状态的分布式实时监测，从而能够提前预警结构疲劳，防止结构损伤，提高系统的安全性和可靠性[2].

对于薄壁结构，光纤测量法的基本原理[3]是：将光纤粘贴到薄壁结构表面进行传感，当结构发生变形时，传感光在光纤内部传输的光程和纤芯的折射率发生改变，从而改变传输光信号的相位.通过干涉原理进行相位解调，获得光纤的微应力，通过应力传递率计算出薄壁结构的应变值.

为了深入研究光纤对薄壁结构应力测量的原理，本文将对光纤感受应力的物理机理进行分析，并建立光纤-薄壁结构理论模型，进行光纤-薄壁结构的应力传递率的推导，计算出应力传递率.运用ANSYS有限元的处理方法，对结构施加两种不同的约束，在10 N和20 N的外力载荷作用下进行仿真，对薄壁结构3个特定区域的应力进行分析，得到应力分布图.

1 光纤对应力的敏感性

应力是描述体积元界面上单位面积作用力的张量.在平衡状态下，体积内部的应力必须平衡.根据胡克(Hooke)定律[2]，在弹性变形的范围内，应力和应变之间存在线性关系.当一段光纤受到轴向施加的外力时，光纤会被拉伸或压缩，即产生了轴向应力.不考虑其他方向的外力，则轴向方向的应力为

(1)

式中：F为轴向力；A为光纤的横截面积.

光纤上产生的应变可以表示为

(2)

式中：ex,ey和ez为由应力产生的正应变；Y为材料的弹性模量；υ为泊松比.

如果轴向力大于0，则光纤被拉伸并且横截面变小；如果反方向加力，同时能保持光纤笔直，则在轴向面被压缩，横截面增大[4].弹性模量Y和泊松比υ是材料的基本参数，测得石英的参数为：Y=6.5×1010N/m2，υ=0.17[5].

由文献[2]和[4]可知，应变会导致弹光效应，即折射率会随着应变的增加而变化.分析轴向应力，光纤的折射率变化量表示为

(3)

式中：n为光纤折射率，Δnx, Δny, Δnz分别为折射率在X,Y,Z三个方向上的分量变化量，p11,p12均为光弹性系数.

将式(2)代入式(3)，可得

(4)

在单模光纤中传输的光波基本上是横模，因此有效折射率变化量近似为

(5)

式中，Δneff为有效折射率变化量；γ为有效弹光系数[6].令γ=-n2[(1-υ)p12-υp11]/2，对于石英材料，在682.8 nm波长时测得弹光系数[5]为p11=0.113，p12=0.252.在近红外波段用这些系数去估计弹光系数不会产生很大误差，可以得到石英光纤的γ=-0.22.与光纤长度的变化量ΔL=ezL相加，轴向应力导致的相移可以写为

Δφ=(1+γ)nkLez≈0.78nkLez,

(6)

式中：L为光纤变化长度；k为应变系数.

将一段光纤粘在机器或建筑待测部位的表面，就可通过光相位测量得到其形变的信息.应力导致的相移可以通过光纤干涉仪去测量.在光纤光栅中，应力导致反射光谱的变化，这体现在光谱的漂移大小上.通过运用互相关运算的方法，将应力变化前后的瑞利散射光谱进行互相关运算，得到互相关峰.比较互相关峰值距离零点的位置，此位置对应的大小就是光谱漂移量的大小，也就是应力的大小[7].

当然，不同的外力施加方式，对于径向方向，光纤的应力分析还有所不同.光纤可以看作圆柱形状，当圆柱体受到径向外力作用时，受力并不是只朝一个方向，而是会产生不同方向的力，并且存在一定的夹角，因此合力方向并不固定.光纤的应力分布发生变化，通过受力分析推导，也可以得到应力的大小.

2 光纤与薄壁结构间应力传递的分析

根据实际工程需求，将光纤贴敷于薄壁结构表面进行光纤传感，对光纤传感器与薄壁结构之间的应力传递进行分析[8].分析模型假设条件[9]为：1)薄壁结构、光纤和中间层均为线弹性材料，轴线方向的应力为均匀拉伸应力；2)各层中检测界面之间均无相对滑移，粘接紧密；3)将光纤纤芯和包层视为一体，具有相同的机械特性[10]；4)应力传递仅考虑沿轴向方向.

光纤粘贴在薄壁结构表面，形成了光纤-中间层-薄壁结构的三层结构，结构模型图如图 1(a)所示.图 1(b)为微元体受力分析示意图.

选取光纤微元体，进行受力分析可得

σghgbg=(σg+dσg)hgbg+bgτ(x,hg)dx,

(7)

即

(8)

同理，对中间层的受力分析可得

(9)

由式(8)和(9)可得

(10)

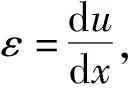
(11)

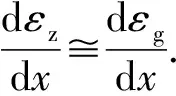
(12)

同理，只考虑薄壁结构水平方向的位移，则

既然谈话内容可以作为证据，那就有可能存在非法取证的情况，如果没有对谈话的过程进行录音录像，就很难还原相关人员的取证行为，也就难以判断言词证据是否应当排除。笔者认为，谈话也可能成为一项重要取证工作，所以监察机关或监察机关委托有关机关和人员进行的谈话也应当对全程进行录音录像，以约束谈话人员的取证行为，保障被谈话人的相关权利。实际上，纪委的相关规定对于审查和调查谈话有录音录像的要求，在纪委和监察委员会合署办公的情况下，监察委员会也应当在法律法规中明确谈话的录音录像问题，这关系到谈话的录音录像在后续司法活动中的运用。

(13)

将式(13)代入到式(12)中，并在[hg,hm]区间内进行积分得到

(14)

积分得

(15)

令

(16)

式中：T为应力传递的滞后系数.则

(17)

将式(17)对x进行求导可得

(18)

对式(18)的求解，可得

εg(x)=C1eTx+C2e-Tx+εm.

(19)

代入边界条件εg(L)=εg(-L)=0, 求解 式(19)得

(20)

式中：εg为光纤的轴向应力；εm为被测物体的轴向应力.式(20)为光纤应力传递方程.

应力传递系数表示为

(21)

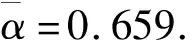
3 应力有限元仿真

对薄壁结构进行有限元分析时，通过对薄壁结构施加水平固定约束和竖直固定约束来模拟仿真薄壁结构不同约束下加载外力时结构应力的变化.

在ANSYS有限元仿真软件中，建立50 cm×50 cm×1 cm的普通钢材质的薄壁结构，其弹性模量为2.1×1011Pa，泊松比为0.3.选取A, B, C三个区域分别施加10 N和20 N的外力载荷，进行静力仿真分析.图 2 为结构网格划分，B区域为结构的中心区域.

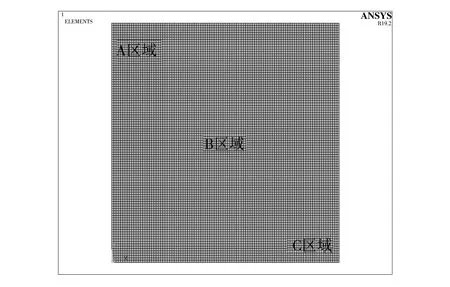
图 2 结构网格划分

对薄壁结构施加约束，模拟薄壁结构实际的固定方式：薄壁结构水平放置时，对其约束的是底面对结构的支撑力，故在仿真时施加的约束是与薄壁结构底面接触到的支撑力，当竖直放置时，对其约束的是结构四周边缘的支撑力，故在仿真时施加的约束是薄壁结构四周边缘的支撑力.

图 3 为水平放置时分别施加载荷的应力分布图.通过分析可以得到Mises等效应力：在10 N外力载荷下，对于不同区域，等效应力最大值分别为0.050 54，0.046 838，0.049 136 MPa；在20 N 外力载荷下，对于不同区域，等效应力最大值分别为0.067 387，0.061 814，0.069 647 MPa.

(f)C区域20 N外力载荷施加

图 4 为水平放置时三个区域同时施加载荷的应力分布图.由图 4 可知：在10 N外力载荷下，等效应力最大值为0.052 23 MPa；在20 N外力载荷下，等效应力最大值为0.069 64 MPa.

(a)A, B, C区域10 N外力载荷施加

图 5 为竖直放置时分别施加载荷的应力分布图.通过分析可以得到Mises等效应力：在10 N外力载荷下，对于不同区域，等效应力最大值分别为0.063 021，0.168 43，0.056 103 MPa；在 20 N外力载荷下，对于不同区域，等效应力最大值分别为0.112 31，0.336 87，0.112 21 MPa.

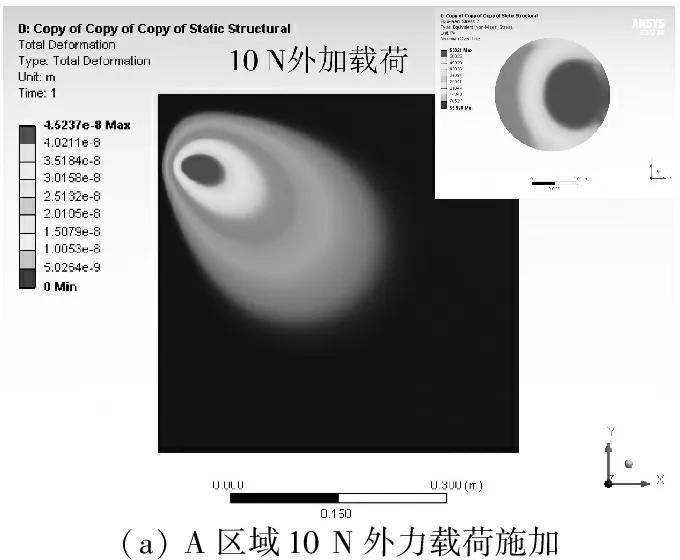
(f)C区域20 N外力载荷施加

图 6 为竖直放置时三个区域同时施加载荷的应力分布图.得到等效应力：在10 N外力载荷下，等效应力最大值为0.168 9 MPa；在20 N外力载荷下，等效应力最大值为0.337 7 MPa.

(a)A, B, C区域10 N外力载荷施加

对比不同外力载荷下，不同区域的等效应力最大值，结果如表 1 所示.

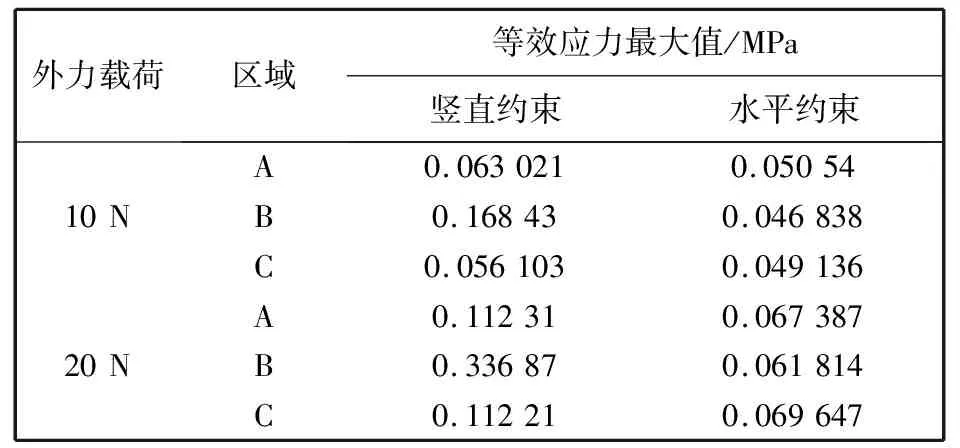
表 1 最大等效应力对比

对理论模型进行静力分析可知，不同的放置方式，薄壁结构在相同外加载荷的作用下，其等效应力不相同，竖直放置的应力比水平放置的要大.这为应力测量系统的搭建和实验测试提供了参考方向.

4 结 论

比较两种固定约束方式，相同的外力施加，薄壁结构的应力大小有很大差别，具体结论如下：

1)水平施加约束时，A, B, C三个区域的应力大小变化不大；在竖直施加约束时，在不同区域施加相同外力载荷，应力的大小会发生较大变化.

2)竖直施加约束时，在薄壁结构的中心区域(B区域)施加外力载荷时，相比于其他区域，该区域的应力最大.而在水平施加约束时，三个区域的应力接近.

3)对三个区域同时施加相同外力载荷，当水平施加约束时，三个区域相互之间的应力相对独立，相互影响不大；当竖直施加约束时，三个区域相互之间的应力会发生抵消融合，相互影响较大.

综上所述，在竖直约束施加时，B区域的应力分布图可以更好地体现光纤-薄壁结构的应力传递特性，同时竖直约束这种施加方式更加符合实验测试过程的薄壁固定方式.在实验测试中可以针对B区域进行反复应力测量，从而验证光纤-薄壁结构的实际应力传递率.