豆粕直剪试验与非线性模型研究

曾长女，王 萌，许启铿，谷 贺，李雪统

河南工业大学 土木工程学院，河南 郑州 450001

豆粕是12种动植物油粕饲料产品中产量最高、用途最为广泛的一种，随着饲料行业对豆粕需求量逐渐增加，做好储藏工作以保证豆粕质量尤为重要。目前，豆粕储存的主要方式：包装粕库储存、散粕立筒仓储存、机械化平房仓储存[1]。豆粕在储存过程中由于自重与仓壁反力的作用，将产生应力与应变，由于摩擦和碰撞的作用会导致豆粕内部应力增加，从而影响其质量，降低其经济价值。豆粕的强度参数是安全设计粮仓的必需参数，其中内摩擦角的确定对粮食储运设备的设计加工、粮堆流动、仓储结构设计等都具有重要作用。部分学者通过直剪试验对大豆的力学特性进行了研究[2-6]，豆粕是大豆提取豆油后得到的副产品，有关豆粕力学特性的研究相对匮乏。

不少学者提出了关于土体、混凝土在内的多种材料的数以百计的本构模型，其中土体的静力本构模型主要包括非线性弹性模型[7-12]和弹塑性模型[13-16]等，这些研究内容极大地加深了对土体的应力变形特性的认识。与土体类似，粮堆由于自重以及外力的作用同样会产生较为复杂的应力-应变关系，为了研究粮堆应力-应变本构关系，国内外众多研究者开始利用土体本构理论以探究粮堆的力学性质。曾长女等[17]通过对豆粕局部变形的测定，将豆粕的应力-应变过程划分为破坏前、破坏与残余3个阶段，并提出不同阶段的应力-应变模型。Xu 等[18]利用直剪仪测定了油菜籽对不同类型材料的内摩擦角和摩擦系数，通过对试验数据的拟合建立了预测模型。Gao等[19]采用改进的Cam-Clay模型，研究了不同颗粒深度和筒仓半径下，在圆形平底筒仓中4个含水层小麦桩的应力分布。蒋敏敏等[20]基于三轴应力路径试验对岩土体三次曲线模型的修正，建立了适于描述仓内小麦粮堆的应力-应变模型，并验证了模型的适用性。陈雪等[21]利用三轴仪对小麦堆进行轴向压缩试验和各向等压压缩试验,通过修正莱特-邓肯模型理论和试验数据，计算得出了小麦堆该模型的14个参数。Ayuga等[22-23]在筒仓卸料数值研究中，提出采用Drucker-Prager模型模拟粮堆的力学性质。高梦瑶等[24]通过三轴压缩试验计算得出不同含水率小麦堆修正剑桥模型参数，并对试验数据进行分析，推导出弹性模量与广义剪切力、平均主应力的关系式。

粮堆在应力作用下孔隙率等方面的变化较土体更大，应变反应速度较土体更为迅速，由于材料不同特性不同，导致粮堆对于本构模型的适用性也不尽相同。目前，粮堆本构理论方面的研究相对于土体较少，粮堆能否完全借助于现有的土体本构模型有待进一步验证。作者引入了Duncan-Chang模型，在直剪试验条件下对豆粕Duncan-Chang模型中各弹性系数的适用性进行分析，确定了模型参数值，用这些参数值描述豆粕直剪试验的剪切变形特性。

1 材料与方法

1.1 材料

试验试样采用河南郑州本地所产豆粕。

1.2 仪器

试验采用粮食直剪仪(图 1)。其中剪切盒外形尺寸为150 mm×150 mm(长度×高度)，上下剪切盒内部均为50 mm×100 mm(半径×高度)的圆柱体。竖向荷载由杠杆比为1∶12的杠杆系统通过传力板施加传递到试样，水平荷载由伺服电机控制器控制伺服电动缸施加，试验采用应变控制的形式，剪切速率的可控制范围为0.01～5 mm/min，可以根据试验要求对剪切速率进行选择。

1.3 试验方法

1.3.1 基本指标测定

根据《粮食、油料检验水分测定法》(GB/T 5497—1985)，将豆粕在105 ℃条件下进行磨碎烘干，测定其含水率为12.34%，根据《粮油检验容重测定》(GB/T 5498—2013)中规定的方法测得其容重为594 g/L，根据《粮食、油料检验比重测定法》(GB/T 5518—1985),测得其比重为1.21。

1.3.2 试验方案

将试样分层装入剪切盒中，保证装样的均匀性。试样安装完成后，首先通过杠杆系统施加竖向应力，然后由伺服电机控制器控制伺服电动缸以一定的剪切速率施加水平剪切力进行剪切试验，试验采用应变控制的形式，对4种不同竖向应力(25、50、75、100 kPa)下的豆粕在不同剪切速率条件(1.2、2.4、3.6 mm/min)下进行直剪试验。

2 试验结果及分析

2.1 豆粕的强度特征

图2a为在剪切速率为1.2 mm/min、4种竖向应力条件下豆粕的剪应力-剪切位移关系曲线。图2b为竖向应力25 kPa下，剪切速率分别为1.2、2.4、3.6 mm/min下的豆粕剪应力-剪切位移关系曲线。

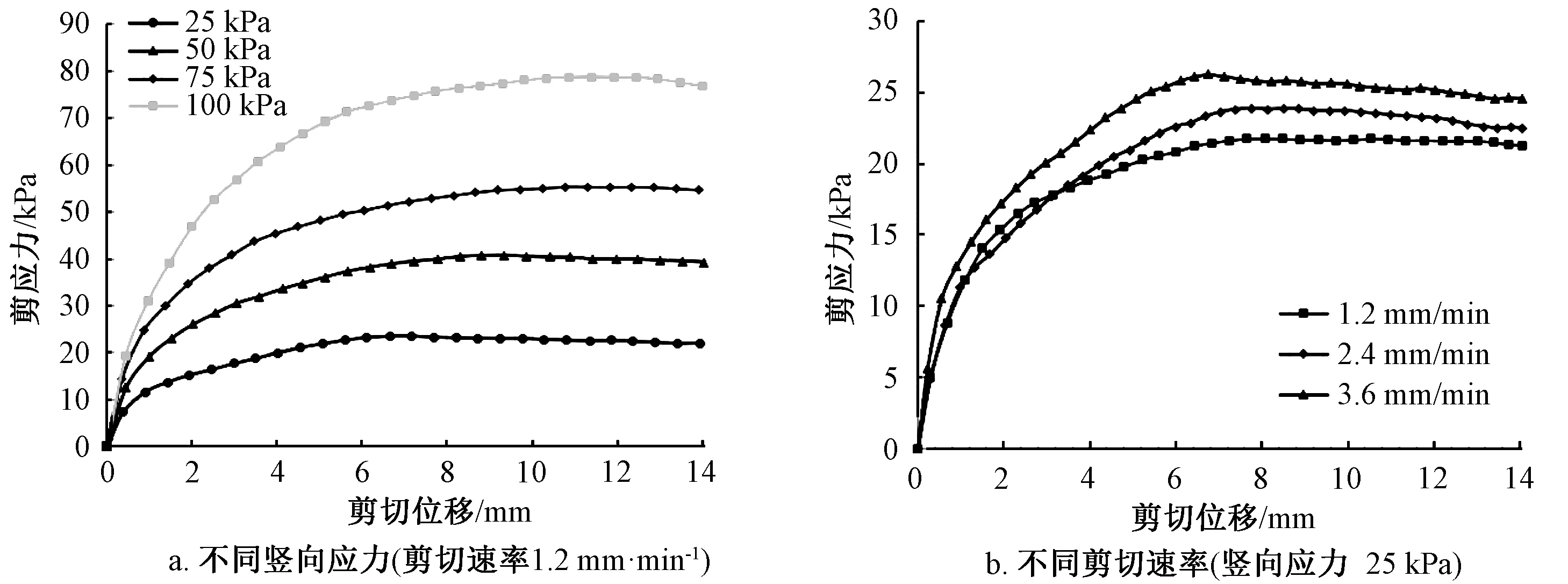
图2 豆粕的应力-应变曲线Fig.2 Stress-strain curves of soybean meal

由图2a可知，随着竖向应力的增大，豆粕的抗剪强度逐渐增大，其达到峰值强度的剪切位移逐渐增大。原因在于竖向应力较低时，豆粕颗粒的位置更容易得到调整，而较大的竖向应力限制了豆粕颗粒的运动，使得豆粕颗粒位置的调整变得更加困难，此时达到稳定状态时的剪切位移会更大。由图2b可以看出，在竖向应力25 kPa下，峰值剪应力随剪切速率的增大而增大。

豆粕的力学特性符合散粒体力学性能，破坏形式接近剪切破坏，其应力-应变关系呈明显的非线性关系，豆粕的应力-应变曲线可以用双曲线模拟，采用Duncan-Chang模型能够很好地反映豆粕的非线性特性。

2.2 豆粕的强度指标

图3为竖向应力25～100 kPa下豆粕试样的抗剪强度包络线，决定系数R2在0.95以上，呈现了良好的线性拟合关系，其规律符合摩尔-库伦准则。摩尔-库伦准则：

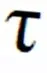
(1)

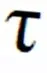
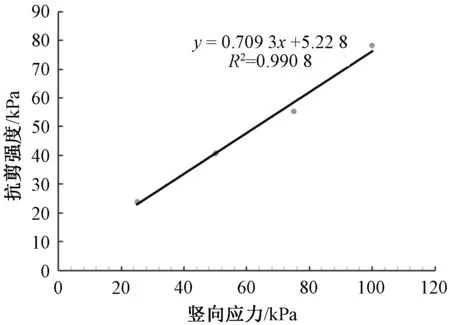
图3 豆粕剪切强度包络线Fig.3 Shear strength envelope of soybean meal

3 豆粕的模型参数研究

3.1 Duncan-Chang双曲线模型分析

由图2所示的剪应力-剪切位移关系曲线可以看出，其应力-应变关系体现了比较明显的非线性关系，即切线模量发生了软化[25]。借助于反应应力-应变曲线非线性本构模型的Duncan-Chang模型进行修正即可以很好地运用到直剪试验结果中[26-27]。根据Kondner的建议，豆粕的应力-应变曲线近似为双曲线，其应力-应变关系满足双曲线方程:

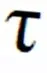
(2)

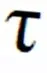
初始剪切模量Ei由Janbu在1963年通过相应的研究发现其随着竖向应力(σn)的变化存在指数函数关系[28]，公式如下：

(3)

式中：K为初始切线模量基数;m为无量纲指数；pa为标准大气压，取101.3 kPa;Ei为初始切线模量，MPa。

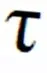
(4)

通过对剪应力-剪切位移曲线上的任意一点进行求导可以获得该曲线上每一点的瞬时剪切模量，所以任意一点的切线模量Et为：

(5)

对式(2)进行微分，并结合式(1)—(4)整理得出邓肯张在1970年提出的切线模量表达式(6)，用于直剪试验。

(6)

3.2 模型参数的确定

将式(2)变形为：

(7)

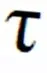
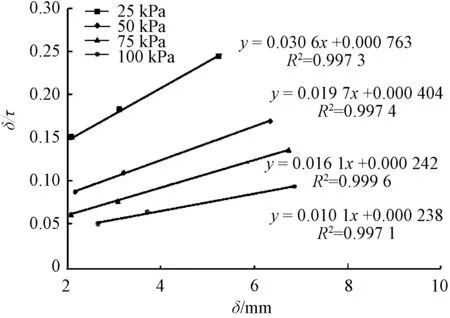
图4 不同竖向应力下曲线Fig.4 Curves of δ/ and δ under different vertical stresses

由图4可知，决定系数R2均接近1，说明豆粕所取点绘制的曲线符合双曲线模型，求得的各个试验参数和破坏比(Rf)见表1。

表1 各试验参数及破坏比结果Table 1 Values of test parameters and failure ratio

Rf作为评价应力-应变曲线是否接近双曲线的标准，其值通常小于1，Rf越接近于1，说明其应力-应变曲线越接近于双曲线，Rf平均值为0.802 1，说明豆粕的应力-应变曲线以双曲线来模拟是可行的。

对式(3)两边取对数可得：

(8)

由式(8)可知，lg(Ei/pa)～lg(σn/Pa)呈线性关系，可以拟合成斜率为m，截距为lgK的直线，对以上双对数关系进行线性回归分析，拟合后的双对数曲线以及各参数值见图5，K=46.259，n=0.886 9。

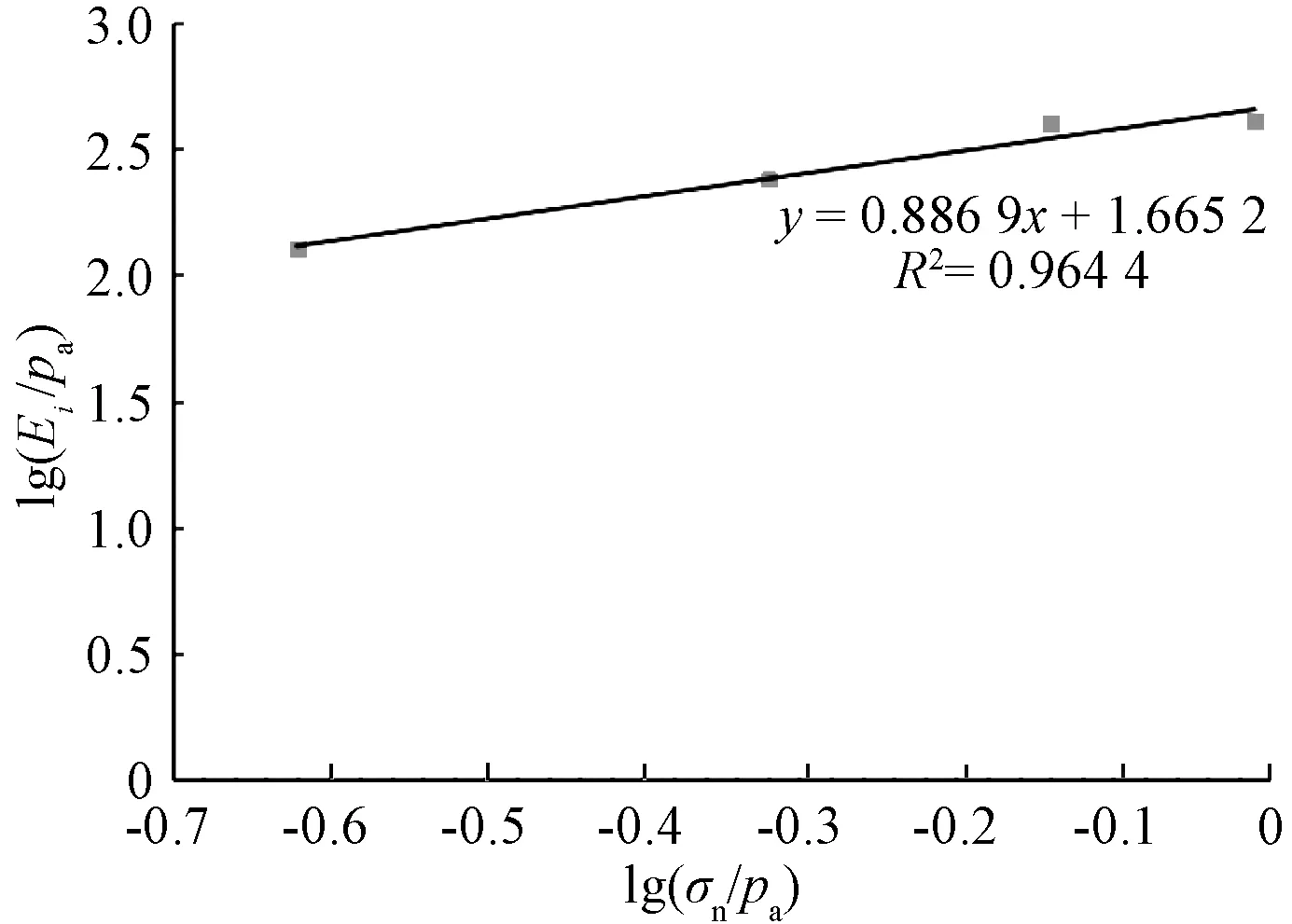
图5 双对数关系拟合曲线Fig.5 Fitting curve in double-logarithmic fitting curve

由图5可得，随着竖向应力的增大，初始剪切模量Ei逐渐增大，其双对数拟合曲线的决定系数R2为0.964 4，大于0.95，说明具有良好的线性拟合关系，即公式(3)和公式(6)适用于豆粕的研究。

3.3 模型的验证

利用模型对本试验的数据进行验算分析，图6为模型预测的应力-应变结果与试验结果的对比情况。4种竖向应力(25、50、75、100 kPa)对应的峰值剪应力误差分别为8.50%、8.92%、0.74%、7.54%，两者在误差允许的范围内吻合程度较好，表明所用模型较合理。

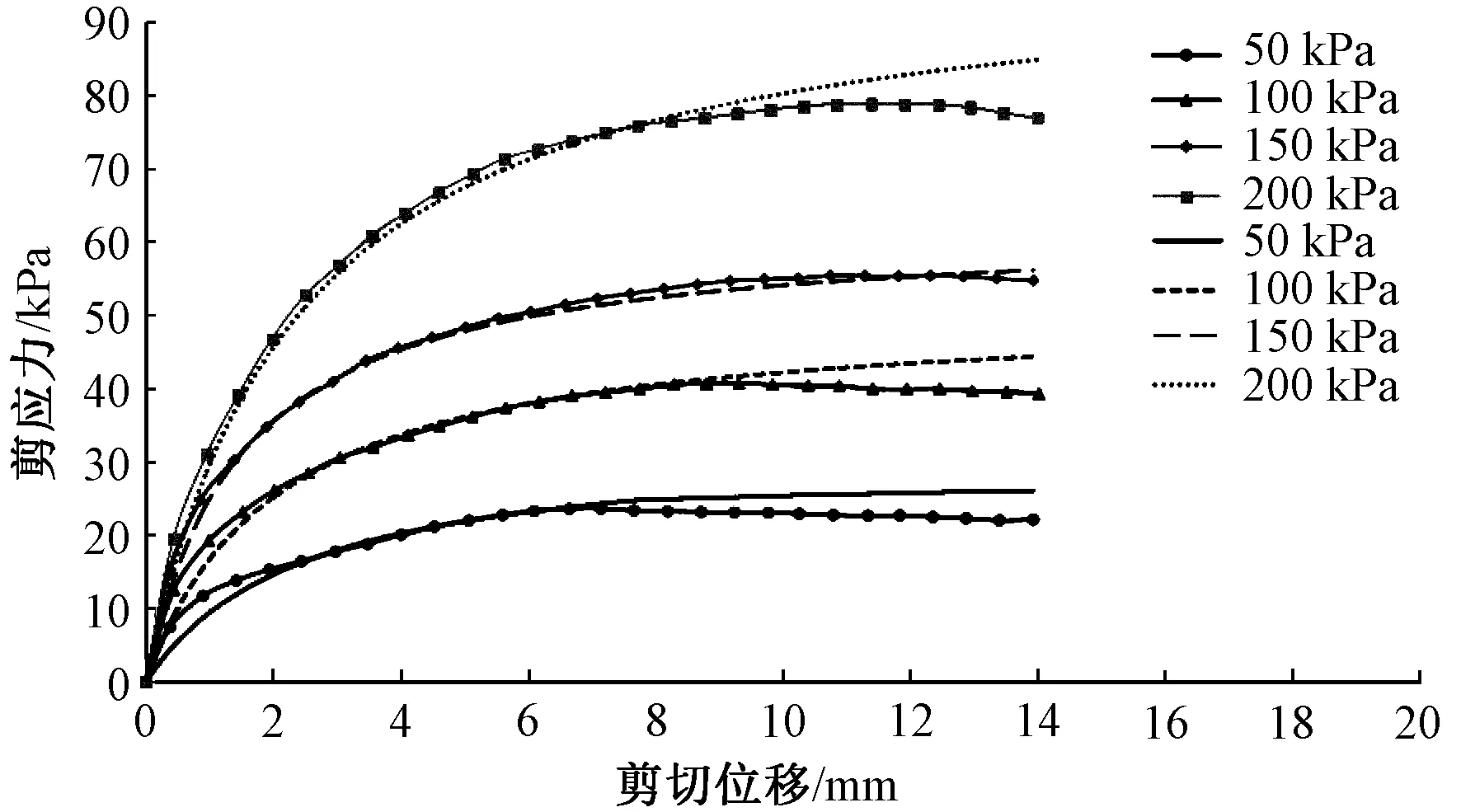
图6 试验和模型预测的应力-应变对比曲线Fig.6 Stress-strain comparison curve predicted by test and model

4 结论

通过直剪试验对豆粕在不同竖向应力和剪切速率下的强度特性进行了分析，引入了Duncan-Chang模型，并分析了Duncan-Chang模型各弹性系数的适用性，得到以下结论：通过豆粕直剪试验获得的剪应力-剪切位移关系曲线，得到了在相同剪切速率下其抗剪强度随着竖向应力的增大而逐渐增大，且达到峰值强度的剪切位移也逐渐增大；在相同竖向应力下，峰值剪应力随着剪切速率的增大而逐渐增大。豆粕的剪切破坏形式符合摩尔-库伦准则，豆粕的应力-应变曲线能够采用双曲线模拟，应力-应变模型符合Duncan-Chang模型。模型预测结果与试验结果吻合较好，其达到的拟合效果较理想，说明所用模型较为合理。获得豆粕Duncan-Chang模型的5个基本参数，分别为咬合应力为5.23 kPa、内摩擦角为35.35°、破坏比为0.802 1、初始切线模量基数为46.259、指数为0.886 9。