基于卡尔曼滤波的车辆液压主动横向稳定杆最优控制研究

赵 强，孙 柱

(东北林业大学 交通学院，黑龙江 哈尔滨 150040)

0 引 言

车辆发生侧倾主要是由于受到强侧向力的缘故，车辆载荷迅速转移引起车身倾斜，过大的侧向力则会致使车辆侧翻。为提高车辆的抗侧倾性及车辆的侧倾极限，通常在车辆上增装传统的被动横向稳定杆。但传统被动横向稳定杆调节能力有限，而主动横向稳定杆能根据汽车行驶工况和车身姿态，实时输出最优的主动抗侧倾力矩，能有效抑制车辆侧倾[1]。

目前主动横向稳定杆系统得到越来越多的认可与应用。德尔福公司研发的自动稳定杆系统(ASBS)已应用到路虎、Jeep等车型上，在提高车辆稳定性、抑制车身侧倾有明显帮助。大陆公司研发的主动式侧倾稳定系统(ARS)即液压式主动横向稳定杆也已应用于宝马5系、7系等部分车型。我国相关学者也对主动横向稳定杆系统进行了相关研究：周兵等[2]通过将PID与线性控制相结合方法，利用主动悬架与主动横向稳定杆的耦合关系，设计了PID集成控制策略；陈志韬[3]提出一种新的主动横向稳定杆结构，通过线性最优二次型控制对车身侧倾进行闭环控制；陈山[4]针对液压式主动横向稳定杆系统提出分层控制算法；赵福民[5]针对性地研究了液压马达式主动横向稳定杆，基于线性化反馈的滑模控制策略对主动控制系统的反馈线性化控制器及滑模变结构控制器进行了设计；丁义兰[6]采用ADAMS-MATLAB联合仿真，设计了一套包含控制单元、各种传感器、激励器及横向稳定杆主体的主动横向稳定杆系统；吕绪宁[7]对汽车主动横向稳定杆与主动前轮转向协调控制进行研究，设计了ARB和AFS的协调控制器，显著改善汽车的横摆稳定性、侧倾性、主动安全性；李真炎[8]使用电机提供驱动力单元的主动横向稳定杆，采用PID控制策略减少车辆在特殊工况下的车身侧倾角，实现了车身侧倾的主动控制；陈祥林[9]针对主动横向稳定控制研究系统，采用模糊滑模控制算法，设计了基于DSP的具有嵌入式C代码自动生成功能的仿真控制平台。

以上学者对主动横向稳定杆的研究均缺乏对车辆侧倾、横摆等状态的估计，而一般进行控制则需要先期获得以上状态信息。笔者针对液压式主动横向稳定杆系统进行了分析、建模，通过建立闭环在线的Kalman滤波观测器，对双移线工况进行实验仿真。对质心侧偏角、横摆角速度、簧上质量侧偏角、簧上质量侧偏角速度等参数进行估计，在上述估计值基础上设计出LQG最优控制器，并基于MATLAB-Simulink进行模型仿真验证。

1 含主动稳定杆车辆模型建立

1.1 主动稳定杆系统工作机理

图1为整车侧倾模型示意。当车辆右转时〔图1(a)〕，车身会发生侧倾〔图1(b)〕，会使稳定杆两个端部连接点产生相反位移，稳定杆被动地发生扭转变形，产生抗扭力矩MARr，传递到车身上即为被动抗侧倾力矩；当侧倾角超过一定阈值时，液压缸开始动作，稳定杆进入主动工作模式，此时右侧液压缸活塞杆回缩，对稳定杆产生一个逆时针(从左侧观察)扭矩Trr，左侧液压缸活塞杆伸出，对稳定杆产生一个顺时针(从左侧观察)扭矩Trf，在后轴主动稳定杆上产生一个主动的合力矩Tr=Trf+Trr，因此在后轴主动稳定杆上产生的总作用力矩为MARr+Tr。该力矩作用在稳定杆上使稳定杆右侧连接点下降，从而减少车身侧倾程度。

1.2 车辆动力学模型

根据图1建立侧向动力学、横摆动力学、车身侧倾动力学、前后轴簧下质量侧倾动力学方程。

动力学方程如式(1)～(5)：

(1)

(2)

(3)

(4)

(5)

式中：m、ms、muf、mur分别为车辆总质量、簧上质量、前轴簧下质量、后轴簧下质量；υ为车辆纵向速度；h、hu分别为簧上质量重心距侧倾中心轴高度、簧下质量重心距地面高度；r为侧倾中心轴距地面高度；β为质心侧偏角；φ、φuf、φur分别为簧上质量侧偏角、前后轴簧下质量侧偏角；Ψ为横摆角；Tf、Tr分别为前后轴稳定杆主动抗侧倾力矩，其中：Tr为图1(b)的Trf和Trr力矩之和，Trf为后轴左侧液压缸产生的主动抗侧倾力矩，Trr为后轴右侧液压缸产生的主动抗侧倾力矩；Tf的组成同Tr；ktf、ktr分别为前后轴轮胎滚动刚度；kf、kr、bf、br分别为前后轴悬架侧倾刚度和阻尼；lf、lr分别为前后轴分别距重心的距离；Ixx、Ixz、Izz分别为簧上质量的转动惯性矩、惯性横摇积、横摆惯性矩；Fyf、Fyr分别为前后轴轮胎侧向力。

Fyf和Fyr可用式(6)、(7)求出：

(6)

(7)

式中：Cf、Cr分别为前后轮胎的线性刚度系数；MARf、MARr分别为稳定杆本体扭转变形引起的抗侧倾力矩。

MARf和MARr对前后轴簧下、簧上质量的影响如式(8)、(9)[10]：

(8)

(9)

式中：KAOf、KAOr分别为前后轴横向稳定杆的扭转刚度；tA为稳定杆水平直杆部分长度的一半；tB为稳定杆与车架两个连接点之间距离的一半；C为稳定杆侧臂部分长度在车身纵向的投影。

1.3 主动稳定杆液压作动器

主动稳定杆抗侧倾力矩是由液压作动器的液压缸两腔压差产生，如图2。这两个腔的压差为ΔP=P1-P2，所产生的推力如式(10)：

Fact=ApΔP

(10)

式中：Ap为液压缸活塞面积。

上述液压缸由伺服阀控制，其负载流量QL的计算如式(11)：

(11)

式中：KX和Kp分别为阀门流量增益和压力系数。

每个腔室如式(12)、(13)：

(12)

(13)

式中：βe为有效体积弹性模量；Cep、Cip分别为外泄漏系数和内泄漏系数。

各腔室容积随活塞位移ya变化如式(14)、(15)：

V1=V01+Apya

(14)

V2=V02-Apya

(15)

式中：V01、V02分别为每个油腔腔室的初始体积。

故各腔室流量方程如式(16)、(17)：

CepP1

(16)

(17)

将式(16)、(17)简化得式(18)：

(18)

式中：Ctp=2Cip+Cep为执行机构总泄漏系数。

由式(11)、(18)可得出伺服液压阀执行机构的动态方程，如式(19)：

(19)

式中：Vt=V01+V02=2V0。

此外，阀芯Xv的位移由电流u控制，忽略伺服阀的滞回效应和流场力对伺服阀性能影响，用1阶模态来近似描述电子伺服阀动态特性，有式(20)：

(20)

式中：τ为时间常数；Kv为电液伺服阀模型增益。

综上所述，通过式(10)、(19)、(20)对伺服液压作动器建模，其中输入信号为电流u，输出信号为力Fact。

在车辆前后稳定杆上分别安装两个上述规格尺寸相同的阀控缸作动器。其中：对应4个伺服阀的4个输入电流分别为：μfl(前左)、μfr(前右)、μrl(后左)、μrr(后右)；对应作动力分别为：Factfl(前左)、Factfr(前右)、Factrl(后左)、Factrr(后右)。故可确定前后轴主动横向稳定杆系统产生的合力矩分别如式(21)、(22)：

Tf=-lactFactfl+lactFactfr

(21)

Tr=-lactFactrl+lactFactrr

(22)

式中：lact为两个执行器之间距离的一半。

将式(21)、(22)进一步简化并将式(4)代入，有式(23)、(24)：

Tf=2lactFact=2lactApΔpf

(23)

Tr=2lactFacr=2lactApΔpr

(24)

式中：Δpf、Δpr为前后轴液压机构内部的压力差。

前后两液压机构活塞位移近似计算如式(25)：

yaf,r=lact(φ-φuf,r)

(25)

将式(10)、(19)、(20)、(25)整合可得阀控缸伺服作动器方程，如式(26)～(29)：

(26)

(27)

(28)

(29)

则其运动微分方程可用线性时不变状态空间表达出来，如式(30)：

(30)

式中：A、B1、B2、C、D1、D2分别为有合适维数的模型矩阵；w为外界干扰；u为控制输入。

将w和u合并成新的U，有式(31)：

(31)

2 Kalman观测器设计

在实际车辆动态模型中，系统输入端存在输入噪声和输出端在实际测量中存在量测噪声，为让模型更接近实际，需将输入、输出方程式中加入输入噪声和量测噪声。因此将式(31)改为式(32)：

(32)

式中：Ξ(t)为路面输入白噪声；θ(t)为量测噪声；这二者均值都为0，且Ξ(t)和θ(t)不相关。

根据Kalman滤波算法确定车辆主动横向稳定杆控制系统的卡尔曼滤波如图3。

利用Kalman滤波算法对系统状态进行估计时需对此刻状态进行估计。首先进行状态一步预测更新[11]，如式(33)：

X(t|t-1)=ΦX(t-1|t-1)

(33)

一步预测协方差更新如式(34)：

P(t|t-1)=ΦP(t-1|t-1)ΦT+HQHT

(34)

Kalman增益矩阵如式(35)：

K(t)=P(t|t-1)CT[HP(t|t-1)HT+R]-1

(35)

状态更新如式(36)：

X(t|t)=X(t|t-1)+K(t)[Z(t)-CX(t|t-1)]

(36)

协方差阵更新如式(37)：

P(t|t)=[I-K(t)C]P(t|t-1)

(37)

至此Kalman滤波观测更新过程就由这5个递推公式进行描述。从一个滤波周期而言，Kalman滤波在使用系统信息和观测信息的先后次序来看，Kalman滤波具有两个明显的信息更新过程：一个是时间更新过程，另一个是观测更新过程。

X(t|t-1)是利用(t-1)时刻的预测结果；X(t-1|t-1)是(t-1)时刻的最优结果；P(t|t-1)是X(t|t-1)对应的协方差；P(t-1|t-1)是X(t-1|t-1)对应的协方差；X(t|t)是t时刻的最优估计值。

由此可看出：卡尔曼滤波能通过递推与实时校正相结合手段来保证其滤波观测的准确性。其重点是对P(t)与K(t)的求取，K(t)=P(t)CT(t)θ-1(t)，故P(t)作为微分黎卡提方程的解如式(38)：

(38)

由于该系统采用的是连续系统下的卡尔曼滤波，对于求解微分黎卡提方程是通过文献[12]所提到的对于滤波问题。当t比较大时，则为代数黎卡提方程解可得知，原微分黎卡提方程的P(t)即为代数黎卡提方程的解。

3 主动横向稳定杆的优化控制

主动横向稳定杆控制系统目标是最大限度地提高车辆侧倾稳定性，定义Rf、Rr为前后轴的横向传递载荷，如式(39)：

(39)

式中：Fzf为前轴总轴重；Fzr为后轴总轴重；ΔFzf和ΔFzr分别为前轴和后轴的横向载荷传递量；lw为同轴轮距的一半。

若正态传递载荷Rf、Rr达到1或-1，则说明车辆已经翻车[13-14]。故在设计主动横向稳定杆时，首先需尽量减少传递载荷Rf、Rr，为此还需将簧上质量和簧下质量φ-φuf,r限制在悬架行程的(7/8deg)之内。以上控制目标的实现是基于LQG方法处理完成的。

LQG优化过程是将性能指标J降到最小，通过控制系统输入u，包括性能特征要求及控制器输入限制，通常表示如式(40)：

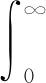
(40)

式中：Q、R分别为正定的加权阵。

最主要目标是要实现使车辆的抗侧倾性能最大化，而φ、Rf、Rr、φ-φuf、φ-φur为直接影响车辆侧倾稳定性的指标，因此加入到性能指标J中；另外还要使控制作用最小，即要使控制液压缸的伺服阀的输入电流(uf、ur)最小，基于这些原因，确定优化性能指标J如式(41)：

(41)

式中：加权参数ρ1=ρ2=ρ3=ρ4=ρ5=Ruf=Rur=1。

根据线性最优控制理论，增益K的最小化形式如式(42)：

K=R-1BTP

(42)

矩阵P为代数黎卡提方程的解，则有式(43)：

AP+ATP-PBR-1BTP+Q=0

(43)

在控制器设计中，所有状态都由上述卡尔曼滤波器最优估计得到。状态反馈控制率如式(44)：

(44)

式中：K为状态反馈增益矩阵。

设计完成的带有Kalman滤波的LQG控制系统流程见图4。

4 仿真验证

基于上述控制设计，笔者将基于Kalman滤波最优控制用到主动横向稳定杆上，并通过Simulink仿真对不带主动控制的被动横向稳定杆与带有Kalman最优控制的主动横向稳定杆进行对比，验证主动横向稳定杆的抑制车身侧倾效果。

以某车型为研究对象，该车辆的主要结构参数及主动稳定杆电液伺服作动器的主要参数参见表1，建立的Simlink模型如图5。

表1 车辆及液压系统主要参数

笔者所建立的车辆模型在仿真时以70 km/h速度行驶。通过车辆在一定车速下的双移线工况，急打方向盘而造成车身侧倾甚至侧翻状况进行仿真观测，方向盘转角如图6。

不带主动控制的被动横向稳定杆与带有Kalman最优估计的主动横向稳定杆的仿真结果对比见图7。由图7(a)、(b)可知：带有传统被动横向稳定杆的车辆簧上质量最大侧倾角及最大侧倾角速度分别为6.3°和13.48(°)/s；前轴簧上质量最大侧倾角为1.57°；后轴簧上质量最大侧倾角为1.59°。而带有主动横向稳定杆的车辆将其簧上质量的最大侧倾角及最大侧倾角速度控制在1.76°和3.82(°)/s；前轴簧上质量最大侧倾角为0.51°；后轴簧上质量最大侧倾角为0.12°。

采用主动横向稳定杆的车辆同比采用被动横向稳定杆的车辆其簧上质量最大侧倾角减少72.06%，簧上质量最大侧倾角速度减少71.66%，前轴簧上质量最大侧倾角减少67.52%，后轴簧上质量最大侧倾角减少92.45%。由此看出：基于Kalman滤波观测器的主动横向稳定杆在抑制车身侧倾方面有着非常出色表现。同时，图7也表明：Kalman滤波观测器能完全预测跟踪最优的控制曲线，即所设计的Kalman滤波能对车辆状态做出实时最优估计。

5 结 语

笔者针对阀控缸液压主动稳定杆系统，建立了整车及主动稳定杆作动器的动力学模型和状态空间模型；并通过设计Kalman滤波观测器来对车辆状态进行最优估计，对液压式主动横向稳定杆进行最优控制；以某车型参数对车辆进行建模，模拟车辆在某一车速下变道，急打方向盘而造成车身侧倾甚至侧翻状况，根据不同输入实时更新最优估计，从而达到对主动横向稳定杆不同抗侧倾力矩的输出。通过在MATLAB/Simulink进行的仿真数据也表明：所设计基于Kalman滤波观测器的主动横向稳定杆能有效抑制车身侧倾，有效提高车辆在行驶中的安全性与舒适性。