基于证据的怀疑

桂海斌

1 引言

怀疑是在知识论的研究中无法避开的一个概念，因为知识论正是在怀疑的声浪中不断发展前行的。以笛卡儿（R.Descartes）为代表的怀疑论者秉持着普遍怀疑原则主张怀疑一切，而维特根斯坦（L.Wittgenstein）则明确地指出，“如果你试图怀疑一切，那么你将不能怀疑任何东西”。（[10]，第115 页）为此，维特根斯坦提出了鲜明的口号：“怀疑来自信念之后”。（[10]，第160 页）无独有偶，波兰尼（M.Polanyi）在明确了毫无限制的怀疑并不能为我们提供新的认识之后，亦提出了“怀疑不能在信托框架之外起作用”的主张。（[5]，第266 页）

尽管维特根斯坦和波兰尼使用的术语不同，但都区分了“合理的怀疑”和“不合理的怀疑”，将普遍怀疑归属于不合理的怀疑范畴，主张合理的怀疑需要理由。（[11]，第59 页）不同于维特根斯坦和波兰尼对“不合理的怀疑”的直接拒斥，普赖尔（J.Pryor）在研究所谓的毫无理由的“不合理的怀疑”时，为我们揭示了一种相信与怀疑共存的认知状态，即仅依据某种不恰当的可能性对一个命题进行怀疑时，认知主体依然可以形成关于该命题的信念。（[7]，第525 页）

简要言之，维特根斯坦和普赖尔研究怀疑时的进路不尽相同，区别在于分别将“有理由的怀疑”和“仅由某种可能性被提出而产生的怀疑”作为各自的主要研究对象，是两个不同层次的怀疑研究进路。本文的侧重点是前者，以信念和怀疑之间的密切关系为切入点，将基于证据的怀疑作为待考察的研究对象。

本文结构如下：第二节，介绍学者已经提出的怀疑的定义，以及对怀疑进行形式化的研究，分析和讨论它们的不足之处。第三节，将怀疑作为静态的认知态度，通过考察与怀疑相关的有效式和非有效式来揭示怀疑的逻辑性质。第四节，将怀疑作为动态的认知过程，考察初始认知状态为相信某个命题，在引入该命题否定的证据集后认知状态所发生的变化，并给出动态算子的归约公理及其有效性的证明。第五节，总结本文的研究工作和得到的研究结果。

2 对怀疑定义的研究

就逻辑的研究而言，对信念的研究已经相当成熟，但对怀疑的逻辑研究却并不多见。要逻辑地研究怀疑，首先需要弄清楚的就是怀疑是什么。萨蒙（N.Salmon）在对怀疑进行研究时，曾对怀疑做了如下的定义（[8]，第1 页）：

·A怀疑p被定义为：A不相信p，或A中止了对p的判断。

–A不相信p被定义为：A相信¬p。

–A中止了对p的判断被定义为：并非A相信p，且并非A相信¬p。

对于萨蒙的定义，撒加德（G.Thagard）直接指出了其中的问题，即对于任意的命题p,要么A相信p，要么A怀疑p。（[9]，第392 页）而从逻辑的角度上看，萨蒙将“不相信p”和“并非相信p”当作了两个不同的概念也是不对的，因为“不”和“并非”都是否定连接词“¬”的体现，换言之，“不相信p”和“并非相信p”表达的是同一个涵义。

奥尔森（E.J.Olsson）和普罗耶蒂（C.Proietti）在研究群体信念时，也曾简要地提到对怀疑的定义（[6]，第503 页）：

· 怀疑p被定义为：不相信p，且不相信¬p。

然而这种定义的问题在于，怀疑p和怀疑¬p没有被区分出来。换言之，依照该定义，在怀疑p的同时，也怀疑¬p。

此外，鲍梅尔（M.M.Bäumel）在形式化维特根斯坦观点的工作中也明确地给出了基于概率理论的怀疑定义（[1]，第36 页）：

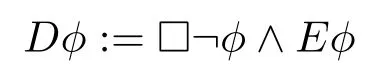
·µ(¬H)≠1∧∃E ⊆W(µ(E)<1∧dwE >t ∧µ(H |E)

依据鲍梅尔提供的定义，“在点w上怀疑一个命题H”需要满足四个具体的要求：(1)¬H的概率小于1；(2)存在证据E且E的概率小于1；(3)dwE表达的是证据E在点w上的安全度，需要E在w点上的安全度比t大1根据鲍梅尔提供的概率方法，阈值（threshold）t 的取值范围是(0.5,1]。E 在w 点上的安全度反映了认知主体在点w 上拒斥E 的意愿，E 的安全度越高，拒斥E 的可能性越小。；(4)给定证据E后H的概率至少要小于t。

与其他学者提出的怀疑的定义有着明显的不同，鲍梅尔提出的定义，将证据因素直接纳入到了怀疑的定义中。该定义的要求(4)，清楚地表达了这样的一个思想，即我们在怀疑命题H时，不相信命题H是因为我们有证据E。但是，以概率的方式对怀疑进行定义，或多或少会带有一定的局限性，即阈值t的取值难免具有一定的主观性，在不同的情景下，t的取值总是不尽相同，而不同的t的取值很可能会导致不同的认知状态。

通过分析和总结学者们关于怀疑的已有研究，不难发现，我们至少还能从两个方面推进对怀疑的形式化研究。一方面，以非概率的方式，继续对基于证据的怀疑进行系统的形式化研究，考察怀疑的逻辑性质；另一方面，除了将怀疑定义为静态的认知态度，我们还可以把怀疑视作是动态的过程进行研究。本文对怀疑的形式化研究，将基于以上两个方面展开。不论是对于作为认知态度的静态怀疑，还是对于作为动态过程的动态的怀疑，本文都将紧紧围绕着证据因素对它们进行分析和研究。

3 静态的怀疑

邻域语义的证据模型，最早是由范丙申（J.van Benthem）和帕奎特（E.Pacuit）共同提出的（[3]，第63 页），用于研究证据和基于证据的信念之间的关系。本文所使用的语义与范丙申等提供的语义的区别在于信念的定义，而不同之处将直接体现在证据和信念之间的关系上。

定义1(语言L).令At为原子公式的集合，基础证据模型语言的递归定义如下：

其中，p ∈At。其它的命题连接词（∨,→,↔）的情况和通常的定义一样。□ϕ读作“认知主体有ϕ的证据”，Bϕ读作“认知主体相信ϕ”以及Aϕ读作“ϕ在所有点上都为真”。将E作为A的对偶算子，Eϕ被定义为¬A¬ϕ。

定义2(证据模型).一个证据模型是一个三元组M=，其中W是一个非空点集，N是一个邻域关系：V是一个赋值函数：我们将N(w)记作为集合{X |w N X}，特别地，对于任意的w ∈W，∅∉N(w)并且W ∈N(w)。如果对于模型M中任意的两个点w和v都有N(w)=N(v)，那么我们称模型M是均衡的证据模型。2定义2 中的证据模型定义引自文献[3]，因其最早在文献[3]中被提出。文献[3]和[2]中的证据模型的定义是无差异的。其中“uniform evidence model”被笔者译为“均衡的证据模型”。所谓“uniform evidence model”的直观理解是，对于每一个“uniform”的证据模型中任意的两个点，它们的邻域都是相同的或无差别的，故而取“均衡”一词，以表达不偏不倚之意。

定义3(极大有穷相交性).一个集簇X是一个W子集的集合，如果对于每一个X的有限子簇{X1,…,Xn}⊆X都有∩1≤i≤n Xi≠∅，那么我们称X具有有穷相交性（f.i.p）。如果X具有有穷相交性，并且没有其它X的扩充具有这个性质，那么我们称X有极大有穷相交性。3定义3 中的极大有穷相交性定义，参考的是范丙申和帕奎特等人对证据模型更进一步的研究中的定义，即文献[2]中的定义。对于极大有穷相交性，文献[2]中的定义（Definition 2.3，在第99 页处）不同于文献[3]的定义（Definition 2.2，在第63 页处）。在帕奎特的专著《模态逻辑的邻域语义》（[4]）的一个章节“证据和信念的逻辑”中，可以找到与文献[2]一样的极大有穷相交性的定义，即文献[4]第33 页中，Definition 1.36 对极大有穷相交性的定义。本文的研究结果是基于文献[2]中的极大有穷相交性的定义展开的，不依赖于文献[3]的极大有穷相交性的定义。

命题1.M=是一个任意的证据模型，w是模型M中任意的一个点。对于任意的极大有穷相交性的簇X ⊆N(w)，都有W ∈X。

证明.假设有一个极大有穷相交性的簇X使得W∉X。根据定义，对于每一个X ∈X，X ⊆W。于是，∩{X ∪W}=∩X。然而，X ⊆{X ∪W}。于是，X就不是极大的。但这与X是一个极大有穷相交性的簇相矛盾。因此原假设不成立。

为了让读者对极大有穷相交性有更加直观的了解，我们将通过具体的证据模型来对它进行说明：

M=是一个证据模型，W={w,u,v}，N(w)={{u},{v},{w,v},{w,u,v}}，N(u)={{u},{w,u},{w,u,v}}，N(v)={{w},{w,u},{u,v},{w,u,v}}，V=∅。

图1:证据模型例示

其中，w的邻域N(w) 中有两个有极大有穷相交性的集簇，分别是X1={{u},{w,u,v}}，X2={{v},{w,v},{w,u,v}}；u的邻域N(u)中有一个有极大有穷相交性的集簇Y，Y={{u},{w,u},{w,u,v}}；v的邻域N(v)中也有两个有极大有穷相交性的集簇，分别是Z1={{w},{w,u},{w,u,v}}，Z2={{w,u},{u,v},{w,u,v}}。

定义4(真值条件).令M=(W,N,V)是一个证据模型，点w ∈W是模型M中任意的一个点。公式ϕ ∈L的真值条件被递归定义为：

·M,wp，当且仅当，w ∈V(p)。

·M,w¬ϕ，当且仅当，

·M,wϕ ∧ψ，当且仅当，M,wϕ，并且M,wψ。

·M,w□ϕ，当且仅当，存在一个有关系wNX的集合X，使得对每一个点v ∈X，都有M,vϕ。

·M,wBϕ，当且仅当，对于每一个具有极大有穷相交性的簇X ⊆N(w)和对每一个点v ∈∩X都有M,vϕ，并且对于任意的X ∈N(w)，倘若存在一个点x ∈X ∈X使得M,x¬ϕ，那么存在另一个点u ∈X使得u ∈∩X。

·M,wAϕ，当且仅当，对于所有的点v ∈W,M,vϕ。

将模型M中所有满足ϕ的点的集合记作可满足性和有效性的定义和它们在标准模态逻辑中的定义一样。

就基于证据的信念而言，我们认为有证据支持ϕ并不意味着认知主体就会相信ϕ。为了相信一个命题ϕ，认知主体需要考虑他所持有的全部证据，具体而言，就是考察证据集中每一个具有极大有穷相交性的证据集簇X。这样的思想，在范丙申等人定义的B算子中就已经被体现出来了。（[3]，第64 页）在他们的基础上，本文对B算子还做了额外的要求：相信一个命题ϕ，就意味在证据集中的每一个证据里，都至少有一个满足ϕ的点。

通过考察公式□ϕ →¬B¬ϕ的有效性，就能够体现出二者的区别。在范丙申等人对证据模型的进一步研究中，曾通过一个无穷模型指出，依据他们对B算子的定义，□ϕ →¬B¬ϕ在所有证据模型的类上不是有效的，仅在这样的证据模型类上才是有效的，即极大有穷相交性簇的广义交集不为空的模型类。4因此，范丙申等在保持信念语义不变的情况下转向研究极大有穷相交性的簇的广义交集不为空的证据模型类。（[2]，第100 页）

依据本文所提供的语义，□ϕ →¬B¬ϕ在所有证据模型的类上也是有效的。就直观理解而言，该命题的有效性体现了证据和信念之间的关系：证据集中有某个命题的证据，就意味着不会相信该命题的否定。从另一个方向上说，相信了某个命题的否定，就意味着，证据集中没有该命题的证据。

命题2.□ϕ →¬B¬ϕ是有效的。

证明.假定M,w□ϕ，根据定义，存在一个证据X ∈N(w)使得又根据定义∅∉N(w)，因此X不是空集。也就是说，X中的每一个点都满足ϕ，并且X中至少有一个点x使得M,xϕ。假设M,wB¬ϕ，首先，根据定义，对于每一个有极大有穷相交性的簇X，都会使得∩X中的每个点都满足¬ϕ。其次，由于X不是空集，于是根据定义，对于每个含有X的簇X，还要求X中存在另一个点u使得u ∈∩X，也就是说，M,u¬ϕ。这就与矛盾了。因此，原假设不成立。

由命题2 很容易联系到引文中已经提到的内容，即在维特根斯坦看来，“合理的怀疑”需要理由。就证据模型而言，怀疑命题ϕ就需要有¬ϕ的证据，这也正是怀疑ϕ意味着不相信ϕ的原因之所在。于此同时，怀疑ϕ也意味着并非模型中所有的点都满足¬ϕ，因为倘若所有的点都满足¬ϕ将会直接拒斥ϕ，而不会怀疑ϕ。因此，本文将怀疑定义为“存在满足ϕ的可能性，但是有¬ϕ的证据”：

将Dϕ读作“ϕ是可疑的”，其真值条件如下：

相应地，与怀疑相关的有效式和非效式主要有：

表1:与怀疑相关的有效式和非有效式

从表1 上看5表1 中的公式有效性的证明参见附录A。，¬Bϕ →Dϕ不是有效的，解决了萨蒙的定义中的问题，即并非对于任意的命题，要么相信该命题，要么怀疑该命题。此外，Dϕ →□¬ϕ的有效性直接表达了怀疑是基于证据的思想，再结合Dϕ →D¬ϕ不是有效的，则解决了奥尔森和普罗耶蒂所提供的定义中的问题，即怀疑状态可以通过审视证据模型中的证据来判定，是怀疑一个命题，还是怀疑一个命题的否定，而不是像奥尔森和普罗耶蒂给出的定义那样，怀疑一个命题的同时，总会怀疑该命题的否定。

□ϕ →¬B¬ϕ是有效的，表达了不相信一个命题的认知状态，是由该命题的否定的证据导致的。再结合Dϕ →¬Bϕ的有效性和Dϕ →□¬ϕ的有效性，不难发现怀疑状态下的不相信状态，正是由引发怀疑的证据所导致的，即在怀疑某个命题ϕ时，不相信ϕ的原因在于有¬ϕ的证据。而这点恰与鲍梅尔提出的定义中的要求(4)是契合的，即我们在怀疑命题H时，不相信命题H是因为我们有证据E。

更进一步的，对D算子的逻辑性质进行考察，发现D(ϕ →ψ)→(Dϕ →Dψ)不是有效的，这说明D算子在分配律上是不成立的。

命题3.D(ϕ →ψ)→(Dϕ →Dψ)不是有效的。

证明.考虑这样的一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)={w}，V(q)=∅。

· 由于，也就是(p →q)，根据定义，M,w□¬(p →q)。又因为，也就是，根据定义，(p →q)。于是，(p →q)。

· 由于M,u并且，根据定义，M,w□¬p。又因为，根据定义，。于是，。但是，由于V(q)=∅，根据定义，M,wEq。于是，M,wDq。因此，M,wDp →Dq。

综上，M,wD(ϕ →ψ)→(Dϕ →Dψ)。

虽然公式D(ϕ →ψ)→(Dϕ →Dψ)不是有效的，但我们总能找到怀疑算子所遵循的规律，比如公式D(ϕ →ψ)→(Aϕ →Dψ)就是有效的。

命题4.D(ϕ →ψ)→(Aϕ →Dψ)是有效的。

证明.假定M,wD(ϕ →ψ)并且M,wAϕ。根据定义，M,wD(ϕ →ψ)当且仅当M,w□¬(ϕ →ψ)∧E(ϕ →ψ)，也就是M,w□(ϕ ∧¬ψ) 并且M,wE(¬ϕ ∨ψ)。再根据定义，M,w□(ϕ ∧¬ψ)当且仅当存在一个X∈N(w)使得X中的每一个点都满足ϕ ∧¬ψ，因此也就存在一个X ∈N(w)使得X中的每一个点都满足¬ψ，即M,w□¬ψ。由于M,wAϕ，故模型中所有的点都满足ϕ，而M,wE(¬ϕ ∨ψ)，也就是模型M中存在一个点满足¬ϕ ∨ψ，因此，模型M中存在一个点满足ψ，即M,wEψ。综上，M,wDψ。

D(ϕ →ψ)→(Aϕ →Dψ)是有效的，该公式有效性的直观意义在于，如果被怀疑的命题是一个蕴涵式，那么，一旦我们确认该蕴涵式的前件在所有的点上都为真，我们的怀疑焦点就会转移到该蕴涵式的后件上。它给予我们的一些启发在于，在推理过程中，怀疑也有着它所遵循的规律，我们通过发现和运用这些规律也可以获得新的认识。

4 动态的怀疑

在第三节将怀疑作为静态算子考察时，通过命题2 得出怀疑某个命题ϕ时，不相信ϕ是因为有¬ϕ的证据。倘若认知主体的初始认知状态是相信ϕ，那么将¬ϕ的证据引入到证据集中后，认知主体的认知状态究竟会发生怎样的变化？

定义5(动态怀疑).M=是一个证据模型，并且ϕ ∈L。怀疑后的模型M¿ϕ=¿ϕ,N¿ϕ,V¿ϕ，其中W¿ϕ=W，V¿ϕ=V，N¿ϕ(w)=N(w)∪{{u} |将[¿ϕ]ψ记作：“如果初始时，相信ϕ且存在着¬ϕ的可能性，那么在怀疑ϕ之后，ψ为真”。它的真值条件如下：

M,w[¿ϕ]ψ，当且仅当，如果M,wBϕ ∧¬Aϕ，那么M¿ϕ,wψ。

通过观察动态怀疑的定义可以发现，被添加到证据模型中的集合不是某一个证据，而是每一个具体的证据的集合。将这样的更新理解为动态怀疑的更新是基于以下两点考虑：(1)每个引发怀疑的可能性都是具体的，即该可能性引发怀疑不仅仅是因为该可能性存在，而是确有支持该可能性的证据。(2)单个的证据被提出时会容易被否掉，因为认知主体往往不会由于单个的证据被提出而直接改变自己的信念，而会检测被提出的单个证据是不是站的住脚，即是否能作为证据被接纳。在科学发展史上，广为人知的对“地心说”的怀疑就是具体的例子。6在哥白尼（Copernicus）正式提出“日心说”之前，由于权威教会对“地心说”的支持，以及在一定时期里依据“地心说”的本轮模型可以在一定程度上正确地预测天象，在生产实践中也起过一定的作用，因而天文学者们相信“地心说”。然而，随着天文仪器的不断完善，观测到的行星实际位置同本轮模型计算结果的偏差逐渐出现。起初，人们并没有认识到这是由于“地心说”本身的错误造成的，为了修正误差，不得不反复地引入本轮来补救“地心说”。到了哥白尼的时代，反复嵌套的本轮已经达近百个，却仍不能满意地计算出行星的准确位置。正是由于彼时每一个具体的偏差的叠加，使得当时的天文学者们转而怀疑“地心说”。

命题5.对于任意的证据模型M和任意的p ∈At，M,w[¿p]Dp。

证明.假定M,wBp ∧¬Ap。由于N¿p(w)=以及M,w¬Ap，又因为在动态变化中V(¬p)=V¿p(¬p)，于是至少有一个单元素集{u}并且M¿p,u¬p，也就是至少存在一个非空的证据X ∈N¿p(w)使得根据定义，M¿p,w□¬p。由于M,wBp ∧¬Ap，也就是M,wBp并且M,w¬Ap。首先，由于M,wBp，根据定义，对于每一个有极大有穷相交性的簇X ⊆N(w)，都有其次，由于M,w¬Ap且W ∈N(w)，再根据命题1，对于每一个有极大有穷相交性的簇X，至少存在一个证据W ∈X，使得W中存在一个点y并且M,y¬p。结合M,wBp，根据B的语义，W中至少存在一个不同于y的点v，使得。又因为W=W¿p并且V(p)=V¿p(p)，故而存在一个点v ∈W¿p，使得M¿p,v p，根据E的语义，M¿p,w Ep。因此，M¿p,w Dp，根据的语义，M,w[¿p]Dp。

命题5 为我们说明了对于任意的原子命题p，如果一个认知主体的初始认知状态是相信p，那么在引入¬p的证据集后，该认知主体就会怀疑p，这也意味着彼时该认知主体不相信p。遗憾的是，命题5 的有效性并不能推广到任意的公式。

不妨考虑这样的一个模型M，其中W={w,u,v}，N(w)={{w,u},{w,v},{w,u,v}}，N(u)=N(v)={{w,v},{u,v},{w,u,v}}，V(p)={w}。根据定义，，，，以及。更进一步地，根据定义，M¿Bp,w ¬Bp，M¿Bp,u ¬Bp和M¿Bp,v ¬Bp，于是M¿Bp,w⊭EBp，根据定义，M¿Bp,w⊭DBp。因此，M,w⊭[¿Bp]DBp。

从技术的角度上说，不能推广到任意公式是由于动态变化后证据集发生了变化，而证据集的变化则会导致证据模型中有极大有穷相交性的簇的重组，形成新的集簇，此举会对B前置的公式在新模型中是否被满足产生很大的影响。尽管命题5 的有效性不能推广到任意的公式，但它也体现出由证据集变化导致的认知状态的改变不是机械的而是灵活的，即我们不能仅简单的考虑新添加的证据来判断认知状态的变化，而更应该重新审视新的证据集，对新形成的证据模型的模型结构做整体的考察。

命题6.ϕ是语言L中的任意公式。如果M=是一个均衡的证据模型，那么对于W中的任意两个点w、v，当且仅当。

证明.命题6 的证明直接依据B和A算子的语义，以及均衡证据模型的性质就可以得出，故证明从略。

就命题6 的直观理解而言，它表达了在任意一个均衡的证据模型中，对于模型中任意的两个点，它们的邻域都是相同的，故而Bϕ ∧¬Aϕ的取值与模型中的点无关。因此，命题6 为我们在均衡的证据模型类上对动态怀疑的性质进行研究奠定了基础。

引理1.令M是任意的一个证据模型，w是模型M中任意的一个点，M¿ϕ是模型M在动态怀疑ϕ后生成的模型。如果，那么其中X是模型M中任意的一个极大有穷相交性的簇，Y是模型M¿ϕ中任意的一个极大有穷相交性的簇。

证明.假定，根据定义，模型M中的每一个极大有穷相交性的簇X，它的广义交集中的每一个点都满足ϕ并且广义交集不是空集，7由于M,w ¬Aϕ，根据定义，也就是W 中存在一个点s，使得M,s ¬ϕ。又根据定义W ∈N(w)，所以模型M 中的每一个极大有穷相交性的簇X 都包含有W。又由于M,w Bϕ，根据定义，对于每一个X，W 中都存在一个不同于s 的点落在∩X 中，且∩X 中的点都是满足ϕ 的。因此，模型M 中的每一个极大有穷相交性的簇X，它的广义交集中的每一个点都满足ϕ 并且广义交集不是空集。即∩X ⊆并且∩X≠∅。由于N¿ϕ(w)=故M¿ϕ中所有极大有穷相交性的簇的集合{Y | Y是模型M¿ϕ中一个有极大有穷相交性的簇}={X | X是模型M中的一个有极大有穷相交性的簇}∪{Z | Z={X1,...,Xn，{u}}，其中并且u ∈X1∈N(w),...,u ∈Xn ∈N(w)}。8就直观理解而言，模型M¿ϕ 中的有极大有穷相交性的簇由两部分组成，其一，是模型M 中原本的那些有极大有穷相交性的簇，因为在动态变化中，被添加到N(w)中的每一个集合都是单元素集，且每个单元素集中的点都满足¬ϕ 的，这些单元素集和M 中原本的有极大有穷相交性的簇的广义交的交必定为空，因为模型M 中的每一个极大有穷相交性的簇X 的广义交集中的每一个点都满足ϕ 且广义交集不是空集，因而，模型M 中原本的那些有极大有穷相交性的簇在动态变化后都被保留了下来；其二，是由模型M 中的证据集和新添加的单元素集，形成的新的有极大有穷相交性的簇，由于是和单元素集形成的极大有穷相交性的簇，这些新形成的有极大有穷相交性的簇，它们的广义交就是一个个的单元素集，且这些单元素集中的点都满足¬ϕ，而这些广义交再并起来，就是¬ϕM。因此，

由于Z是仅由某个单元素集合{u}和原模型M中某些含有点u的证据构成的，因此∩Z就是{u}。于是，

定理1.以下归约公理在均衡的证据模型类上是有效的：

证明.归约公理1–3 是分别关于原子命题和布尔公式的情况，它们分别与范丙申等给出的“证据添加”的归约公理EA1、EA2和EA3相对应（[3]，第73 页），相应的归约公理的有效性证明方法也是一样的。因此，归约公理的有效性证明将聚焦于[¿ϕ]Aψ、[¿ϕ]□ψ和[¿ϕ]Bψ的情况。

令M为任意的均衡证据模型，w、u、v、x、y、z、s是模型M中任意的点。归约公理4–6 的证明如下：

· 归约公理4 的证明。要证[¿ϕ]Aψ ↔((Bϕ∧¬Aϕ)→A[¿ϕ]ψ)在均衡的模型类上是有效的，需证M,w[¿ϕ]Aψ当且仅当M,w(Bϕ∧¬Aϕ)→A[¿ϕ]ψ。M,w[¿ϕ]Aψ，当且仅当（根据¿的语义），如果，那么M¿ϕ,w Aψ，当且仅当（根据A的语义），如果，那么对于每一个点v ∈W¿ϕ使得M¿ϕ,v ψ，当且仅当（根据命题6 和定义），如果，那么对于每一个点v ∈W使得M,v[¿ϕ]ψ，当且仅当（根据A的语义），如果，那么[¿ϕ]ψ，即M,w(Bϕ ∧¬Aϕ)→A[¿ϕ]ψ。

· 归约公理5 的证明。要证[¿ϕ]□ψ ↔((Bϕ ∧¬Aϕ)→(□[¿ϕ]ψ ∨¬A¬(¬ϕ ∧[¿ϕ]ψ)))在均衡的模型类上是有效的，需证M,w[¿ϕ]□ψ当且仅当M,w(Bϕ ∧¬Aϕ)→(□[¿ϕ]ψ ∨¬A¬(¬ϕ ∧[¿ϕ]ψ))。

（⇒）假设M,w[¿ϕ]□ψ，那么根据¿的语义，如果，那么M¿ϕ,w□ψ。根据□的语义，也就是，如果，那么存在一个X ∈N¿ϕ(w)使得由于N¿ϕ(w)=N(w)∪{{u} |因此，有且仅有两种情况会分别使得模型M¿ϕ中的w满足□ψ：

–X是模型M中的一个证据，即X ∈N(w)。怀疑ϕ后会有ψ的证据，是因为X中的每一个点x在怀疑后会满足ψ，即M¿ϕ,xψ，根据命题6 和¿ 的语义，M,x[¿ϕ]ψ。因此，在这种情况下原模型有M,w□[¿ϕ]ψ。

–X是的某个单元素子集{u}，换言之也就有。怀疑ϕ后会有ψ的证据，是因为模型M中满足¬ϕ的点u在怀疑ϕ后都会满足ψ，即M¿ϕ,uψ，根据命题6 和¿的语义，M,u[¿ϕ]ψ。也就是，[¿ϕ]ψ。因此，在这种情况下原模型有(¬ϕ ∧[¿ϕ]ψ)。

综上，如果，那么M,w□[¿ϕ]ψ或者(¬ϕ∧[¿ϕ]ψ)，根据定义，即M,w(Bϕ ∧¬Aϕ)→(□[¿ϕ]ψ ∨¬A¬(¬ϕ ∧[¿ϕ]ψ))。（⇐）假设M,w(Bϕ ∧¬Aϕ)→(□[¿ϕ]ψ ∨¬A¬(¬ϕ ∧[¿ϕ]ψ))，根据定义，即如果，那么M,w□[¿ϕ]ψ或者(¬ϕ ∧[¿ϕ]ψ)。

– 倘若M,w□[¿ϕ]ψ，那么根据□的语义，存在一个X ∈N(w)，使得X中的每一个点x都有M,x[¿ϕ]ψ。根据命题6 和¿ 的语义，M¿ϕ,x ψ。由于于是，X ∈N¿ϕ(w)。根据□的语义，M¿ϕ,w□ψ。

– 倘若(¬ϕ∧[¿ϕ]ψ)，也就是M,w⊭¬A¬(¬ϕ∧[¿ϕ]ψ)，那么根据A的语义，至少存在一个点u ∈W使得M,u⊭¬(¬ϕ∧[¿ϕ]ψ)，也就是并且M,u[¿ϕ]ψ。根据命题6 和¿的语义，M¿ϕ,uψ。由于于是，{u}∈N¿ϕ(w)。根据□的语义，M¿ϕ,w□ψ。综上，如果，不论是M,w□[¿ϕ]ψ，还是(¬ϕ ∧[¿ϕ]ψ)，都能得出结论M¿ϕ,w□ψ。因此，如果，那么M¿ϕ,w□ψ。再根据¿的语义，M,w[¿ϕ]□ψ。

· 归约公理6 的证明。要证[¿ϕ]Bψ ↔((Bϕ ∧¬Aϕ)→(B[¿ϕ]ψ ∧A(¬ϕ →[¿ϕ]ψ)))在均衡的模型类上是有效的，需证M,w[¿ϕ]Bψ当且仅当M,w(Bϕ ∧¬Aϕ)→(B[¿ϕ]ψ ∧A(¬ϕ →[¿ϕ]ψ))。

（⇒）假设M,w[¿ϕ]Bψ，那么根据¿的语义，如果，那么M¿ϕ,w Bψ。再根据B的语义，如果，那么对每一个极大有穷相交性的簇Y ⊆N¿ϕ(w)和其广义交集中的每一个点v ∈∩Y,都有M¿ϕ,v ψ，并且对于任意的Y ∈N¿ϕ(w)，倘若存在一个点y ∈Y ∈Y使得M¿ϕ,y ¬ψ,那么存在另一个点z ∈Y使得z ∈∩Y。根据引理1，我们有：

如果，根据B的语义，N(w)中的每一个极大有穷相交性的簇X，它的广义交集中的每一个点都满足ϕ，并且广义交集不是空集。又每一个包含集合的极大有穷相交性的簇X的广义交集就是{u}。对于每一个Y ∈N¿ϕ(w)，Y中都存在一个点z使得z ∈∩Y。而对于每一个点

综上，如果，那么[¿ϕ]ψ并且(¬ϕ →[¿ϕ]ψ)，根据定义即M,w(Bϕ ∧¬Aϕ)→(B[¿ϕ]ψ ∧A(¬ϕ →[¿ϕ]ψ))。

（⇐）假设M,w(Bϕ∧¬Aϕ)→(B[¿ϕ]ψ∧A(¬ϕ →[¿ϕ]ψ))，根据定义，即如果，那么[¿ϕ]ψ并且(¬ϕ →[¿ϕ]ψ)。如果，那么根据B的语义，N(w)中的每一个极大有穷相交性的簇X的广义交集中的每一个点x都满足ϕ，并且广义交集不是空集。由于[¿ϕ]ψ，再根据B的语义，对于每一个的x ∈∩X，M,x[¿ϕ]ψ，再根据命题6 和¿的语义，M¿ϕ,xψ。由于(¬ϕ →[¿ϕ]ψ)，根据A的语义，对每一个s ∈W，[¿ϕ]ψ。于是，对于每一个M,z[¿ϕ]ψ。再根据命题6 和¿的语义，M¿ϕ,z ψ。于是，对于每一个都有M¿ϕ,v ψ。根据引理1，我们有：

因此，对每一个极大有穷相交性的簇Y ⊆N¿ϕ(w)，其广义交集中的每一个点v,都有M¿ϕ,v ψ，并且∩Y≠∅。9根据引理1，由于X≠ ∅且因此Y≠ ∅。于是，对于任意的Y ∈N¿ϕ(w)，倘若存在一个点y ∈Y ∈Y使得M¿ϕ,y ¬ψ，那么始终有一个点t ∈Y使得t ∈∩Y。根据B的语义，M¿ϕ,w Bψ。再根据¿的语义，M,w[¿ϕ]Bψ。

推论1.算子E前置公式的归约公理[¿ϕ]Eψ ↔((Bϕ ∧¬Aϕ)→E[¿ϕ]ψ)，在均衡的证据模型类上是有效的。

证明.令M为任意的均衡证据模型，w和v是M中任意的点。要证[¿ϕ]Eψ ↔((Bϕ ∧¬Aϕ)→E[¿ϕ]ψ)在均衡的证据模型类上是有效的，需证M,w[¿ϕ]Eψ当且仅当M,w(Bϕ ∧¬Aϕ)→E[¿ϕ]ψ。

假设10倘若M,w ⊭Bϕ ∧¬Aϕ，那么根据¿的语义和→的真值条件，很容易证得M,w [¿ϕ]Eψ 当且仅当M,w (Bϕ ∧¬Aϕ) →E[¿ϕ]ψ。，M,w[¿ϕ]Eψ，当且仅当（根据假设和¿的语义），M¿ϕ,w Eψ，当且仅当（根据E和A互为对偶算子），M¿ϕ,w ¬A¬ψ，当且仅当(根据假设和¿的语义），M,w[¿ϕ]¬A¬ψ，当且仅当（根据假设和定理1)，[¿ϕ]A¬ψ，当且仅当（根据¬的真值条件），M,w⊭[¿ϕ]A¬ψ，当且仅当（根据假设和定理1），M,w⊭A[¿ϕ]¬ψ，当且仅当（根据A的语义），存在一个点v ∈W使得[¿ϕ]¬ψ，当且仅当（根据¬的真值条件），存在一个点v ∈W使得M,v⊭[¿ϕ]¬ψ，当且仅当（根据假设和定理1），存在一个点v ∈W使得M,v⊭¬[¿ϕ]ψ，当且仅当（根据¬的真值条件），存在一个点v ∈W使得M,v[¿ϕ]ψ，当且仅当（根据E的语义），[¿ϕ]ψ，当且仅当（根据假设和定义），M,w(Bϕ ∧¬Aϕ)→E[¿ϕ]ψ。

就推论1 的直观理解而言，它表达了在怀疑ϕ后的模型中有一个点满足ψ，当且仅当，在怀疑ϕ前的模型中有一个点，该点在怀疑ϕ后会满足ψ。

推论2.算子D前置公式的归约公理[¿ϕ]Dψ ↔((Bϕ ∧¬Aϕ)→((□[¿ϕ]¬ψ ∨¬A¬(¬ϕ ∧[¿ϕ]¬ψ))∧E[¿ϕ]ψ))，在均衡的证据模型类上是有效的。

证明.令M为任意的均衡证据模型，w是M中任意的点。若要证明[¿ϕ]Dψ ↔((Bϕ ∧¬Aϕ)→((□[¿ϕ]ψ ∨¬A¬(¬ϕ ∧[¿ϕ]ψ))∧E[¿ϕ]ψ))在均衡的证据模型类上是有效的，需证M,w[¿ϕ]Dψ当且仅当M,w(Bϕ ∧¬Aϕ)→((□[¿ϕ]ψ ∨¬A¬(¬ϕ ∧[¿ϕ]ψ))∧E[¿ϕ]ψ)。

M,w[¿ϕ]Dψ，当且仅当（根据¿的语义），如果，那么M¿ϕ,w Dψ，当且仅当（根据D的语义），如果，那么M¿ϕ,w□¬ψ ∧Eψ，当且仅当（根据∧的真值条件），如果，那么M¿ϕ,w□¬ψ并且M¿ϕ,w Eψ，当且仅当（根据定理1 和推论1），如果，那么M,w□[¿ϕ]¬ψ ∨¬A¬(¬ϕ ∧[¿ϕ]¬ψ) 并且[¿ϕ]ψ，当且仅当（根据∧的真值条件），如果，那么M,w(□[¿ϕ]¬ψ ∨¬A¬(¬ϕ ∧[¿ϕ]¬ψ))∧E[¿ϕ]ψ，即M,w(Bϕ ∧¬Aϕ)→((□[¿ϕ]¬ψ ∨¬A¬(¬ϕ ∧[¿ϕ]¬ψ))∧E[¿ϕ]ψ)。

相较于推论1 而言，推论2 的直观则稍显复杂，它表达了在怀疑ϕ后的模型中怀疑ψ，当且仅当，第一，在怀疑ϕ前的模型中，要么有一个证据，该证据中每一个点在怀疑ϕ都满足¬ψ，要么模型中至少有一个满足¬ϕ的点，并且该点在怀疑ϕ后会满足¬ψ；第二，在怀疑ϕ前的模型中有一个点，该点在怀疑ϕ后会满足ψ。

概言之，在第四节中，我们对怀疑的动态特征、动态怀疑导致的证据模型变化的机制进行了研究。在对怀疑的动态特征进行考察时，我们延续了由证据导致怀疑的研究思想，从对动态怀疑的理解出发，结合实例提出从相信一个命题到怀疑一个命题，是由于有新的证据被添加到证据集中。接着，我们展现了新证据被添加到证据集后，对整个证据模型的影响，并指出对于模型变化的考察，不能仅简单的考虑新添加的证据，而更应该重新审视新的证据集，需要对新形成的证据模型的模型结构做整体的考察。最后，为了研究动态逻辑的完全性，我们从均衡的证据模型类的性质着手，证明了相应的引理、定理（归约公理）和推论。就所得的技术结果而言，归约公理有效性的证明为整个公理系统的完全性证明提供了基础。

5 结束语

本文研究工作开展的初衷，是考虑到怀疑在西方哲学上（尤其是在西方知识论上）所发挥的重要作用，于是希望通过借助逻辑的工具，对怀疑的性质进行形式化的考察。

在已有的研究中，有的学者提出了怀疑的定义，也有的学者着手开展对怀疑进行形式化研究的工作，或借助于经典模态逻辑，或与概率理论相结合。本文在回顾了学者们已有的研究的基础上，分别讨论了他们提出的怀疑定义的特征。在揭示了已有的怀疑定义的不足之处后，本文提出在邻域语义的证据模型中，分别对静态的怀疑和动态怀疑做了形式化的研究。

一方面，将怀疑作为一种静态的认知态度，并将其定义为“存在满足ϕ的可能性，但是有¬ϕ的证据”，明确了基于证据的怀疑所需满足的条件。该定义不仅为既不相信一个命题也不怀疑该命题的认知状态保留了空间，还明确了怀疑一个命题时不相信该命题，是由于有该命题否定的证据所导致的。另一方面，将怀疑作为动态的过程，给出了动态怀疑算子的语义，并说明了动态怀疑导致证据模型发生变化的机制。接着，在具体展现了动态怀疑引发的证据集的变化后，在均衡的证据模型类上给出了相应的归约公理，并对它们的有效性进行了证明。

需要明确的是，本文在第四节中所呈现的动态怀疑，只是从“相信一个命题ϕ”到“怀疑一个命题ϕ”的动态变化，而动态怀疑并不仅此一类。通常，我们在认知过程中还会经历“从对命题ϕ毫无概念”到“怀疑一个命题ϕ”的动态变化。就证据模型而言，它意味着怀疑前的证据模型“既没有ϕ的证据，也没有¬ϕ的证据；既不相信ϕ，也不相信¬ϕ”。对这类动态怀疑的探究，将是未来的研究方向之一。

此外，在引文中已经提到，本文的研究对象是基于证据的怀疑，而在西方知识论的发展历程中，仍有许多关于非证据的怀疑的研究讨论。非证据的怀疑往往与知识关系密切。因此，在证据模型中考察和探究非证据怀疑的静态特征、动态特征以及和知识的关系，亦是做进一步研究的方向之一。

A 附录

A.1 有效式的证明

以下是表1 中有效式的具体证明。

命题7.Dϕ →□¬ϕ是有效的。

证明.倘若，那么根据定义，M,w□¬ϕ∧Eϕ。根据定义，M,w□¬ϕ。

命题8.D(ϕ ∨ψ)→(Dϕ ∨Dψ)是有效的。

证明.倘若(ϕ ∨ψ)，那么根据定义，M,w□¬(ϕ ∨ψ)∧E(ϕ ∨ψ)。根据定义，M,w□¬(ϕ ∨ψ)并且(ϕ ∨ψ)。

·M,w□¬(ϕ ∨ψ)，当且仅当（根据定义），存在一个X ∈N(w)使得对于每个点v ∈X，都有(ϕ ∨ψ)，当且仅当（根据定义），存在一个X ∈N(w) 使得对于每个点v ∈X，都有，也就是并且。那么，根据定义，我们就可以得出M,w□¬ϕ并且M,w□¬ψ。

·(ϕ ∨ψ)，当且仅当（根据定义），存在一个点u ∈W，使得，当且仅当（根据定义），存在一个点u ∈W，使得或，当且仅当（根据定义），或。

倘若，那么根据定义可得，根据定义，；倘若，根据定义同样可得。

综上，。

命题9.Aϕ →¬Dϕ是有效的。

证明.倘若，那么根据定义，对每一个点v ∈W，都有。因此，M,w⊭□¬ϕ，根据定义，M,w⊭Dϕ，也就是。

命题10.A¬ϕ →¬Dϕ是有效的。

证明.倘若，那么根据定义，对每一个点v ∈W，都有。因此，M,w⊭Eϕ，根据定义，M,w⊭Dϕ，也就是。

命题11.□ϕ →¬B¬ϕ是有效的。

证明.参见命题2。

命题12.Dϕ →¬Bϕ是有效的。

证明.倘若，根据定义M,w□¬ϕ ∧Eϕ，于是，M,w□¬ϕ。再根据□¬ϕ →¬Bϕ是有效的，可得。

命题13.D(ϕ →ψ)→(Aϕ →Dψ)是有效的。

证明.参见命题4。

A.2 非有效式的证明

以下是表1 中非有效式的具体证明。

命题14.D(ϕ ∧ψ)→(Dϕ ∧Dψ)不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)={w,u}，V(q)={w}。

· 由于，根据定义，(p ∧q)。，并且，根据定义，M,w□(¬p∨¬q)，也就是M,w□¬(p∧q)。因此，(p ∧q)。

· 由于并且，根据定义，M,w⊭□¬p，根据定义，M,w⊭Dp。因此，M,w⊭Dp ∧Dq。

综上，M,w⊭D(p ∧q)→(Dp ∧Dq)。

命题15.(Dϕ ∧Dψ)→D(ϕ ∧ψ)不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)={w}，V(q)={u,v}。

· 由于，根据定义，。由于并且，根据定义，M,w□¬p。根据定义，。

· 由于，根据定义，。由于，根据定义，M,w□¬q。因此，。

· 由于M,w⊭p∧q，M,u⊭p∧q并且M,v⊭p∧q，根据定义，M,w⊭E(p∧q)。根据定义，M,w⊭D(p ∧q)。

综上，M,w⊭(Dp ∧Dq)→D(p ∧q)。

命题16.D(ϕ ∨ψ)→Dϕ不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)=∅，V(q)={w}。

· 由于并且，根据定义，M,w□(¬p∧¬q)，也就是M,w□¬(p ∨q)。由于，因此，。根据定义，(p ∨q)。根据定义，(p ∨q)。

· 由于V(p)=∅，根据定义，M,w⊭Ep。根据定义，M,w⊭Dp。综上，M,w⊭D(p ∨q)→Dp。

命题17.(Dϕ ∨Dψ)→D(ϕ ∨ψ)不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)={w}，V(q)={u,v}。

· 根据定义，。11由于所构造的证据模型和命题15 的证明所用证据模型是一样的，M,w Dp 可直接参照命题15 的证明。因此，。

· 由于M,w⊭¬p ∧¬q，M,u⊭¬p ∧¬q并且M,v⊭¬p ∧¬q，根据定义，M,w⊭□(¬p∧¬q)，也就是M,w⊭□¬(p∨q)。根据定义，M,w⊭D(p∨q)。

综上，M,w⊭(Dp ∨Dq)→D(p ∨q)。

命题18.(Dϕ →Dψ)→D(ϕ →ψ)不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)=∅，V(q)=W。

· 由于V(p)=∅，因此，M,w⊭Ep。根据定义，M,w⊭Dp。根据定义，。

· 由于M,w⊭p ∧¬q，M,u⊭p ∧¬q并且M,v⊭p ∧¬q，根据定义，M,w⊭□(p ∧¬q)，也就是M,w⊭□¬(p →q)。根据定义，M,w⊭D(p →q)。

综上，M,w⊭(Dp →Dq)→D(p →q)。

命题19.D(ϕ →ψ)→(Dϕ →Dψ)不是有效的。

证明.参见命题3。

命题20.Dϕ →¬D¬ϕ不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)={w}。

· 由于，根据定义，。由于并且，根据定义，M,w□¬p。根据定义，。

· 由于，根据定义，。由于，根据定义，M,w□p。根据定义，，也就是M,w⊭¬D¬p。

综上，M,w⊭Dp →¬D¬p。

命题21.Dϕ →D¬ϕ不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)={u}。

· 由于，根据定义，。由于，根据定义，M,w□¬p。根据定义，。

· 由于M,w⊭p和M,v⊭p，根据定义，M,w⊭□p。根据定义，M,w⊭D¬p。综上，M,w⊭Dp →D¬p。

命题22.¬Bϕ →Dϕ不是有效的。

证明.考虑这样一个证据模型M，其中W={w,u,v}，N(w)=N(u)=N(v)={{w},{u,v},{w,u,v}}，V(p)=∅。

· 在给定的证据模型中有两个极大有穷相交性的簇，X1={{w},{w,u,v}}和X2={{u,v},{w,u,v}}，其中，∩X1={w}，∩X2={u,v}。由于V(p)=∅，因此，M,w⊭p，于是根据定义，M,w⊭Bp，也就是。

· 由于V(p)=∅，根据定义，M,w⊭Ep。根据定义，M,w⊭Dp。综上，M,w⊭¬Bp →Dp。