费奇悖论的混合时态认知逻辑分析

张玉志

1963 年，美国逻辑学家费奇（F.B.Fitch）证明从证实原则“真命题都是可知的”可以推出“真命题都是已知的”这种荒谬的结论，后人称之为费奇悖论（Fitch Paradox）（[7]）。由于费奇悖论产生于假设“真命题都是可知的”成立，因此它也被称为可知性悖论（Knowability Paradox）。如何消解费奇悖论一直是非经典逻辑和分析哲学的前沿性问题，包括范丙申（J.van Benthem）和达米特（M.Dummett）在内的众多国际著名逻辑学家和哲学家对此高度关注。目前，针对费奇悖论已经形成多种消解方案，例如直觉主义逻辑解决方案（[1,16]）、弗协调逻辑解决方案（[2]）、情景理论解决方案（[6]）、达米特解决方案（[5]）、坦南特解决方案（[15]）、动态认知逻辑解决方案（[3]）、分布式知识解决方案（[10]）、结构证明论解决方案（[9]）、一阶混合模态逻辑解悖方案（[11]）等等。虽然解悖方案有很多，但是各种解悖方案自身都存在问题（[13]，第466 页），这使得到目前为止在费奇悖论上尚未取得一致意见。国内逻辑学界对费奇悖论的研究侧重于介绍国外研究成果，近些年的相关研究可以参考[17–20]。本文在分析证实原则和摩尔句子的思想之后发现：在认知算子上加入时间坐标能够澄清认知公式1本文中所说的“认知公式”仅指含有认知算子K 的公式，如摩尔公式p ∧¬Kp。的准确思想，进而可以消解费奇悖论。据此，可以从混合时态认知逻辑的角度来消解费奇悖论。希望本文的研究视角和结论能够引起学界的关注和讨论。

1 费奇悖论的产生

产生于19 世纪30 年代至40 年代初的实证主义是科学主义思潮的源头，创始人是法国哲学家孔德（A.Comte）。实证主义继承了经验派的基本观点（知识来源于经验），同时开始关注命题的意义问题。实证主义者认为应该放弃对神学、形而上学的讨论，因为真正有认知意义的命题应该是那些可以被经验检验的命题（[21]，第12–14 页）。换句话说，真命题都是可知的，这被称为证实原则（Knowability Principle）。证实原则是实证主义和之后出现的反实在论（Anti-realism）所共同认可的原则。1963 年，美国逻辑学家费奇从证实原则推出“真命题都是已知的”这种荒谬的结论。具体推导过程如下：

令p表示命题变元，◇表示模态算子“可能”，□表示模态算子“必然”，K表示认知算子“知道”，∃表示存在量词，∀表示全称量词。

证实原则在文献中通常被形式化为1 式：p →◇Kp，读作“如果p，那么可能主体知道p”。另外一个事实：人们在任何时候都不是全知全能的，即总是存在一些真命题是人们不知道的。这被称为非全知原则（Non-omniscient Principle），文献中通常将此形式化为2 式：∃p(p ∧¬Kp)。据此，可以例示为3 式：p ∧¬Kp。然后，将3 式代入1 式得4 式：(p ∧¬Kp)→◇K(p ∧¬Kp)。3 式和4 式根据分离规则可得5 式：◇K(p ∧¬Kp)。根据认知逻辑的S5系统可知，K(p ∧¬Kp)不可能为真，并且5 式为假，证明如下：

(1)K(p ∧¬Kp) 假设

(2)Kp ∧K¬Kp(1)，S5系统内定理K(p ∧¬Kp)→(Kp ∧K¬Kp)

(3)Kp ∧¬Kp(2)，S5系统公理Kp →p

(4)¬K(p ∧¬Kp) (1)(2)(3)，归谬法

(5)□¬K(p ∧¬Kp) (4)，必然化规则

(6)¬◇K(p ∧¬Kp) (5)，对偶算子定义

5 式与(6)式相互矛盾。因此，如果坚持证实原则1 式是正确的，那么就必须承认非全知原则2 式是错误的，即必须承认所有真命题都是已知的，∀p(p →Kp)。从一个合理的假设得出一个荒谬的结论，费奇悖论由此而形成。

费奇悖论一经产生，立即引起逻辑学家和哲学家们的恐慌。它的巨大破坏力主要表现为两点：第一，将实证主义、反实在论等哲学流派的理论置于流沙之上；第二，它所得出的荒谬结论直接质疑分析哲学和认知逻辑的存在意义——如果承认所有真命题都是已知的，那么这意味着“知识”和“真”是同一回事（Kp ↔p），并且意味着认知逻辑会完全坍塌为经典命题逻辑。逻辑学家和哲学家们显然不能容忍费奇悖论的存在。自1963 年费奇悖论产生至今，如何对其进行消解一直是国际逻辑学界和哲学界所迫切关心的问题。

2 自然语言分析

费奇悖论直接形成于将摩尔公式“p∧¬Kp”代入证实原则的通俗表达式。据此，想要深入分析费奇悖论必须先澄清两个问题：证实原则的准确思想是什么？摩尔句子的准确思想是什么？对这两个问题的澄清有助于我们找到形成费奇悖论的真正原因。

2.1 证实原则的准确思想

实证主义者所认可的命题不仅包括那些已经被经验证实（证伪）的命题，还包括那些尚未确定真值但在原则上可以被证实（证伪）的命题，例如，外星人存在，哥德巴赫猜想成立等等。虽然这类命题至今尚未被人类证实（证伪），但它们在原则上都可以被证实（证伪），都是“可知的”。需要指出的是，此处所说的“可知的”并不是指这个命题在当下可能被主体知道，而是指此命题在原则上可以被经验检验，或者说原则上可以被知道。具体来说，证实原则中的“可知的”应该是指一定存在一个时间点，在那个时间点上主体知道给定的真命题。因为那个时间点虽然总是存在，却在很多情况下无法确定，所以说给定的真命题只是可以被知道。例如，“如果哥德巴赫猜想成立，那么可能主体知道哥德巴赫猜想成立”是一种完全错误的说法（假命题），因为按照可能世界理论即使哥德巴赫猜想事实上成立，但目前为止没有一个可能世界中有主体（已经）知道这个命题成立。我们应该这样来理解说话者的意思：如果哥德巴赫猜想成立，那么总是存在一个时间点（此处是指将来的一个时间点），在那个时间点上主体知道哥德巴赫猜想成立。

上述分析表明，证实原则“真命题都是可知的”并不是指真命题都在当下可能被主体知道，即将证实原则形式化为“p →◇Kp”是完全错误的。笔者认为，证实原则传递出人们探索真理的勇气和信心，应该把它理解为：任一真命题都会在某个时间点上（过去、现在或者未来）被知道，即对每个真命题而言都存在一个时间点使得在这个时间点上它被主体知道。例如，“北京是中国的首都”是真命题，它在过去已经被人们知道。再比如，人们至今不知道命题“外星人存在”的真值，但是人们相信这个命题的真值在未来的某个时间点上可以被经验检验。同理分析非全知原则，它是指“每个时间点上，总是存在一个命题使得在此时间点上人们知道它”。

2.2 摩尔句子的准确思想

“p ∧¬Kp”被称为摩尔公式（Moore-formulas），它是对“p并且主体不知道p”这样一类摩尔句子（Moore-sentences）的形式化（[4]，第107 页）。在公开宣告逻辑中，摩尔公式的典型特点是被宣告之后不可能被主体知道。例如，考虑a向b宣告“小李是北京人，可是你还不知道”这种情况。a的宣告内容可以用公式“p ∧¬Kbp”2p ∧¬Kbp 仍是摩尔公式。K 算子不加下标时所指范围更广，可以表示人们（群体）知道或者某人知道；K算子加下标时仅指某人知道。来表示，宣告之前公式p ∧¬Kbp是真的，宣告之后它变成假的（因为宣告之后b已经知道小李是北京人）。

当a向b宣告“小李是北京人，可是你还不知道”时，a想要表达的准确思想是什么？可以首先肯定的是，a想要表达的思想不可能是“小李是北京人，并且在我宣告之后你不知道小李是北京人”，因为这本身就是一个假命题。在认知逻辑中，知道公理“Kp →p”是指主体知道的东西都是真的，即人们不可能知道假命题。实际上，a想要表达的思想应该是：小李是北京人，并且在a宣告之前b不知道小李是北京人。a想要表达的思想在宣告之前是个真命题，在宣告之后它仍然是个真命题。显然，此处如果不解释摩尔语句中的“不知道”所指的具体时间，那么摩尔公式“p ∧¬Kbp”所断定的思想实际上是含混的。因此，摩尔句子的形式化需要通过加入时间坐标的形式才能澄清自身的准确思想。

2.3 原因分析及对策

根据非全知原则，摩尔句子“p并且主体不知道p”可以是真命题。但是，第一节中的形式证明说明知道摩尔句子会导致矛盾，即主体永远不可能知道一个摩尔句子。出现这种现象的原因是什么？可以以a向b宣告“小李是北京人，可是你还不知道”这种情况为例进行分析。实际上，a想要表达的思想应该是：小李是北京人，并且在a宣告之前b不知道小李是北京人。而这个复合命题在a宣告之后会成为一个既成事实，并且在a宣告之后会成为b的新知识。换句话说，事实上，在宣告之后b知道“小李是北京人，并且在a宣告之前b不知道小李是北京人”。显然，此处的“b知道”与“b不知道”所处的时间点是不同的。这说明事实上人们可以知道一个摩尔句子，只是人们知道一个摩尔句子的时间与摩尔句子本身中所含有的“不知道”的时间是不同的。

上述分析说明，费奇悖论的出现是因为在形式化证实原则和摩尔句子时没有考虑时间因素。换句话说，费奇悖论的出现是因为认知公式本身表达了含混的思想造成的。巧合的是，日本学者佐藤（M.Sato）在1977 年给出的KT5系统刚好可以在技术上解决这个问题（[14]）。

KT5系统是一种广义上的时态认知逻辑（Temporal Epistemic Logic）3一般认为，时态认知逻辑是时态逻辑和认知逻辑相结合的产物（形式语言中含有时态算子和认知算子），本文称之为狭义上的时态认知逻辑。KT5 系统的形式语言中不含时态算子，但每个认知算子都被一个时间点标注，因此也含有时态。。它的基本形式语言包括原子命题集{p,q,...}、主体集{O,S1,S2,...}和对应正整数集的时间集{t1,t2,t3,...}，其中，主体集中的“O”表示一个特殊的个体“傻瓜”。合式公式递归定义为“φ::=p|⊥|φ →φ|[St]φ”，公式“[St]φ”结合了时态与认知，读作“在时刻t，主体S知道φ”。按此理论，摩尔公式“p ∧¬Ksp”应该被修正为“p ∧¬[St]p”,读作“p并且主体S在t 时刻不知道p”。显然，KT5系统在每个认知算子上加入一个时间坐标，它可以使认知公式所表达的思想更加准确。

3 混合时态认知逻辑的解悖分析

由第二节的分析可知，澄清费奇悖论关键要解决两个问题：第一，在形式化证实原则时必须表达出“对任意真命题，总存在一个时间点使得主体知道它”这层思想；第二，摩尔句子的形式化必须考虑时间因素。KT5系统可以澄清摩尔句子，能够解决第二个问题。但是，KT5系统本身不含量词，不能对时间点进行约束，因而仍然不能解决第一个问题。已知混合逻辑的表达力强于认知逻辑（模态逻辑），并且含有全局算子（存在算子），这直接启发我们可以利用混合逻辑来同时解决上述两个难题。

我们需要先给出混合时态认知逻辑的形式语言及其语义。

3.1 混合时态认知逻辑

定义1(形式语言).给定一个可数的常原子命题集P，p ∈P；有穷主体集Agents，a ∈Agents；自然数集N（时间点的名字，标签集），i ∈N。混合时态认知逻辑的形式语言归纳定义如下：

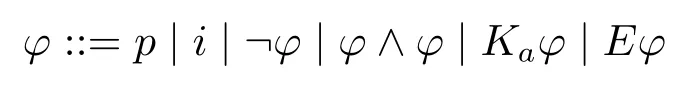
其中，i为原子公式；Kaφ表示主体a知道φ；Eφ表示存在一个时间点使得φ成立。另外，定义@iφ=E(i ∧φ)，表示在一个名字为i的时间点上φ成立。对∨,→,↔的定义如常。

定义2(模型).给定一个可数的常原子命题集P，一个有穷主体集Agents，a ∈Agents，时间点集T，自然数集N，i ∈N。混合时态认知逻辑的模型M是一个六元组(T,<,F,W,R,V)，其中：

(1)T是时间点的集合，t ∈T；

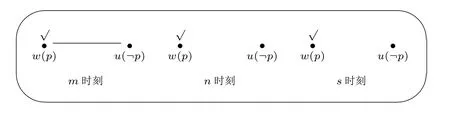
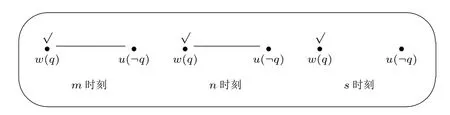
(2)<是T上的一个反自返且传递的二元关系，可以看成是“早于–晚于关系”，m

(3)F是一个函数：N →T，表示每个自然数i仅指称一个时间点；

(4)W为可能世界的集合；

(5)R是一个函数：Agents×T →℘(W ×W)。任意R(a,t)满足以下两个条件：

1 等价关系（自返、传递和对称）；

2 单调递减：对任意m,n ∈T，a ∈Agents，如果m

(6)V是一个赋值函数，P →℘(W)。

关于函数R的定义在直观上是指为不同时间点上的每个主体指派一些不可区分世界。要求R单调递减目的是使每个主体的不可区分世界有序对的集合随着时间的延伸只可能收缩而不可能扩大，直观上是指随着时间的流逝每个主体的不可区分世界越来越少。

定义3(语义).给定模型M=(T,<,F,W,R,V)，公式φ在点模型(M,w,t)上是真的记为M,w,tφ。若公式φ在所有基于框架(T,<,W,R)的点模型上都是真的，则称φ为有效式，记为φ。对M,w,tφ归纳定义如下：

从上述定义可以看出：常原子命题p的真值只跟可能世界有关，不会随着时间发生变化；原子公式i在点模型(M,w,t)为真是指i指称的时间点是t；Kaφ在点模型(M,w,t)为真是指主体a在t时刻从w上看到的所有世界上φ为真；Eφ在点模型(M,w,t)为真是指存在一个时间点t′ ∈T，使得φ在(M,w,t′)上为真；@iφ在点模型(M,w,t)为真是指在w世界上从时间点t跳跃到一个时间点名字为i的点模型上，φ为真。

命题1.@mKap →@nKap，m

证明.反证法。假设上式无效。所以，存在点模型(M,w,t)使得1 式M,w,t@mKap以及2 式M,w,t¬@nKap成立（m

命题1 是指主体总会知道自身在先前时刻的所有知识（特指常原子命题），它说明主体对常原子命题的知识可以进行积累。

有了上述语形和语义定义后，我们就可以准确形式化出证实原则和摩尔句子的思想，同时可以在模型上给出合理解释。

3.2 混合时态认知逻辑解悖方案

在上述混合时态认知逻辑的视野下，证实原则“真命题都是可知的”可以形式化为1 式：φ →EKaφ。它读作“如果φ，那么存在一个时间点使得主体a在那个时间点上知道φ。摩尔句子可以形式化为2 式：p∧@i¬Kap。它读作“p并且在i时主体a不知道p”。将2 式代入1 式，利用分离规则得3 式：EKa(p∧@i¬Kap)。3 式读作“存在一个时间点使得主体a在那个时间点上知道‘p并且在i时主体a不知道p’”。虽然我们可以继续对3 式运用推演规则，但是却不会再推出矛盾。由此，费奇悖论被消解。

上述解悖方案的效果如何？本文以对如下两类命题的分析为例进行作答。令n表示当前时间点，m

第一类，已证实命题。假设命题“小李是北京人（p），可是大家还不知道”为真。由于命题p当前已经被证实，在本文的解悖方案中它需要被形式化为“p ∧@m¬Kp”，表示“小李是北京人，可是在m时大家对此不知道”。在当前时间点n，大家已经知道p，并且大家知道在m时大家不知道p。因此，公式“p ∧@m¬Kp”是当前已知的，也是已经被经验证实的，符合证实原则。公式“p ∧@m¬Kp”在m时没有被大家知道，这符合非全知原则。令w,u分别表示两个可能世界，命题p仅在w世界上为真，则在m时刻主体不能区分w,u两个可能世界，在之后的n,s时刻主体可以区分这两个可能世界。模型如下图1（其中，√标注的世界为现实世界）：

图1

第二类，未证实命题。假设命题“哥德巴赫猜想成立（q），可是人们还不知道”为真。由于命题q当前尚未被证实，在本文的解悖方案中它需要被形式化为“q ∧@n¬Kq”，表示“哥德巴赫猜想成立，但在n时人们对此不知道”。因为q命题事实上尚未被证实并且存在很大难度，所以可能在n+1,n+2,n+3 等很长的一段时间内它都无法被证实。但是，实证主义者相信：只要q是个真命题，就总会存在一个时间点s使得在s时q被人们知道，并且在s时人们还知道在n时人们不知道q。因此，公式“q ∧@n¬Kq”仍然是可知的，也仍然是可以被经验检验的，符合证实原则。公式“q ∧@n¬Kq”在s之前不被人们知道，这符合非全知原则。令w,u分别表示两个可能世界，命题q仅在w世界上为真，则在m,n时刻主体都不能区分w,u两个可能世界，但在之后的s时刻主体可以区分这两个可能世界。模型如下图2（其中，√标注的世界为现实世界）：

图2

上述分析表明，本文给出的混合时态认知逻辑解悖方案可以从技术上消解费奇悖论。注意，从时态角度来消解费奇悖论的研究思路在文献[6,8,12]等已经出现。本文工作与这些研究工作类似但是不同，主要体现在下述三点：第一，本文不使用任何时态算子和关系符号，因此形式语言更为简洁；第二，本文坚持在认知算子上加入时间坐标（把认知句子理解为某人在某时知道某事），而不是“某人知道某事在某时成立”；第三，本文所给模型更为简化，这主要得益于在定义1 中使用了常原子命题。因此，本文的解悖方案是一种更加简洁的方案。

4 结语

直观上，人们可以知道一个摩尔句子。但是，经典认知逻辑从技术上证明了知道一个摩尔公式会导致矛盾。得出这种错误结论是因为逻辑学家没有意识到人们“知道”摩尔公式的时间与摩尔公式本身含有的“不知道”时间是不同的。经典认知逻辑只能对知识的“静态分布”进行模型研究，不能在技术上区分上述两个时间点是导致费奇悖论的关键。换句话说，使用经典认知逻辑的技术来处理知识的“动态分布”（不同时间点上的知识）是不恰当的。于是，消解费奇悖论的关键在于扩张经典认知逻辑，使得人们的认知状态能够被时间点精确标记。