钛合金切削加工参数优化数学模型及工艺参数分析研究*

杜红春，张 祺

(1.江苏食品药品职业技术学院 基础部，江苏 淮安 223002；2.攀枝花学院 智能制造学院，四川 攀枝花 617000)

0 引 言

钛合金材料在加工过程中，由于加工参数选择不合理，会导致材料存在变形问题。有必要对钛合金切削加工参数进行优化，提出精度更高的数学模型；并在建立的数学模型的基础上，讨论加工参数对切削力的影响。

实际工程优化问题通常需要建立一个或者是多个优化目标函数，在特定的条件和约束下实现工程优化[1]。代理模型是解决实际工程优化问题关键技术之一，能够以少量样本数量建立满足工程实际使用的数学模型[2]，同时减少了物理试验次数，提高了优化效率[3]。代理模型是一种主要包含试验设计和近似方法的建模方法，试验设计为代理模型的建立提供了数据样本。根据样本抽取方式不同，试验设计方法主要有全因子试验、BOX-BEHNKEN、中心组合设计、正交试验、拉丁超立方试验、优化拉丁超立方试验、均匀设计等[4-5]。近似方法则主要包括了包括多项式响应面(PRSM)[6]、径向基函数(RBF)[7]、Kriging模型[8]、人工神经网络(ANN)[9]、支持向量回归(SVR)[10]、基因表达编程[11]等多种代理模型方法。Kriging模型是一种常用的近似方法，由Krige提出[12]。为提高其精度，学者们先后对其进行了改进和优化，特别是利用智能算法对其变异函数参数进行优化。如朱恒军等人[13]采用改进灰狼优化算法,优化了Kriging模型的变异函数参数；李晨霖等人[14]采用PSO算法优化了Kriging模型变异函数参数；薛小锋[15]利用GA算法对模型的变异函数进行了寻优；刘辉元等人[16]用模拟退火算法，提高了其理论变异函数拟合精度；刘夏等[17]用模拟退火和人工蜂群，对Kriging模型变异函数进行了优化。

为研究不同样本数据建立Kriging模型的精度问题，笔者探讨不同试验方法产生的数据样本对Kriging模型精度的影响；同时在最佳的试验设计方案基础上，采用量子粒子群算法对传统的Kriging算法进行改进,优化变异函数参数,以提高Kriging算法的拟合精度。

1 克里金代理模型

Kriging(克里金)模型在解决非线性程度较高的问题时，可较容易获得理想的拟合结果，其插值结果定义为已知样本函数响应值的线性加权，即：

(1)

式中：fj(x)—函数，一般为多项式；βj—相对应的系数；Z(x)—静态随机过程，其满足均值为0，方差为σ2。

且对于设计空间内不同两点处，所对应的随机变量之间的协方差为：

Cov[Z(xi),Z(xj)]=σ2R(xi,xj)

(2)

(3)

式中：R(xi,xj)—相关性函数，它表示不同位置处随机变量之间的相关性，常用的相关性函数为高斯型函数。

式(3)中的θ为Kriging模型的变差函数的参数，其大小通过极大似然估计法求解优化问题的方式来确定：

(4)

为保证Kriging预测值与真实函数值之间的均方根误差(RMSE)最小，可得到Kriging模型的近似表达式为：

(5)

2 试验设计

2.1 切削仿真试验因素水平

参考文献[18]，笔者讨论建立切削速度、进给量以及刀具前角3个参数与切削力的之间的数学模型。切削速度、进给量以及刀具前角3个参数各取3个水平，则切削仿真试验因素水平表如表1所示。

表1 切削仿真试验因素水平表

2.2 试验设计及其响应

笔者研究不同试验方法产生的数据样本对KRIGING模型精度的影响，分别对文献中的3个因素3个水平进行BOX-BEHNKEN试验[19]、正交试验[20]、优化拉丁超立方试验[21]、全因子试验[22]，然后分析得到的试验及其主切削力响应情况。

全因子试验设计及其切削力响应如表2所示。

表2 全因子试验设计及其切削力响应

BOX-BEHNKEN试验设计及其切削力响应如表3所示。

表3 BOX-BEHNKEN试验设计及其切削力响应

正交试验设计及其切削力响应如表4所示。

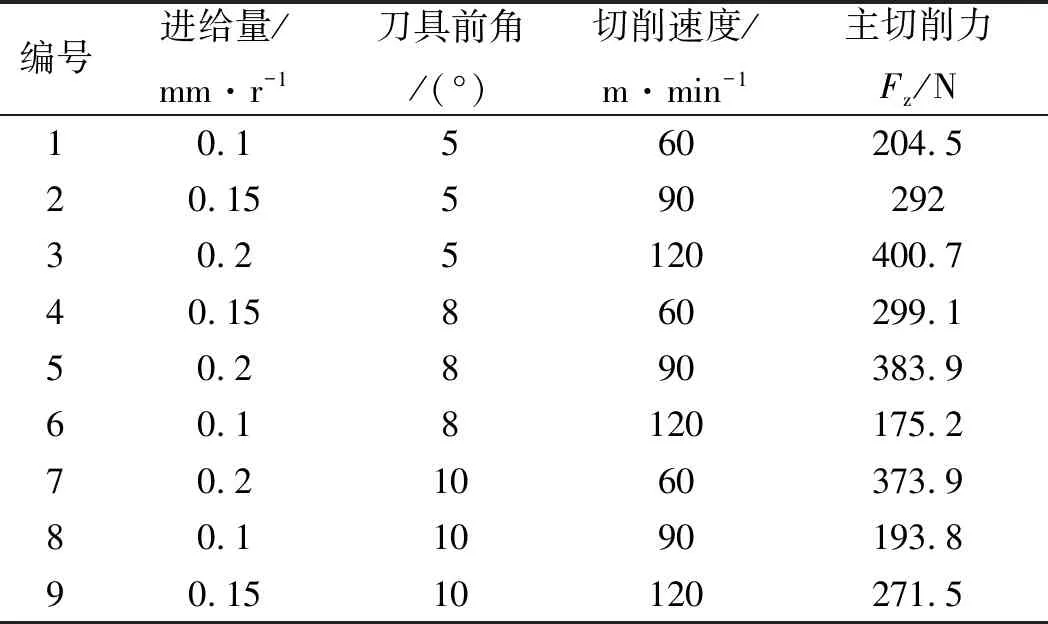
表4 正交试验设计及其切削力响应

优化拉丁超立方试验设计及其切削力响应如表5所示。

表5 优化拉丁超立方试验设计及其切削力响应

3 基于不同试验设计的主切削预测模型精度研究

3.1 模型指标情况

根据参考文献,对于代理模型的模型精度检验指标，目前主要使用确定性系数(R2)、均方根误差(RMSE)和相对最大绝对值误差(RMAE)。其中，前2个指标主要表征了模型的全局近似精度，相对最大绝对值误差(RMAE)则用于反映模型的局部精度[23]。根据参考文献[24]，其数学表达式为：

(6)

(7)

(8)

R2越接近于1，表明代理模型全局逼近的效果越好；RMSE越小，则代理模型的精度越高；RMAE值越小，表明代理模型的精度越高。

根据第4节中的试验设计及其响应值，基于不同试验设计的主切削预测模型指标情况如表6所示。

表6 基于不同试验设计的主切削预测模型指标情况

根据表6中的BOX-BEHNKEN试验、正交试验、优化拉丁超立方试验、全因子试验4种试验设计方法下建立的kriging代理模型，R2指标都大于0.9，属于可用的范围。其中，全因子试验为最好，其次是全因子试验；RMSE指标中，全因子试验接近于0，正交试验为6.944 3，小于BOX-BEHNKEN试验和优化拉丁超立方试验；RMAE指标中，全因子试验接近于0，正交试验为0.243 8，小于优化拉丁超立方试验，但大于小BOX-BEHNKEN试验。

根据确定性系数(R2)、均方根误差(RMSE)和相对最大绝对值误差(RMAE)的情况可知，全因子试验最优，其次是正交实验。但是全因子试验需要对所在可能的试验进行全面试验，加大了试验成本，效率不高；综合判断正交试验的效果相对而言更好。

3.2 主切削力预测结果残差分析

笔者采用BOX-BEHNKEN试验、正交试验、优化拉丁超立方试验、全因子试验方法建立的Kriging近似模型，对全因子试验及其主切削力响应表中的主切削力进行预测。

BOX-BEHNKEN试验残差图如图1所示。

图1 BOX-BEHNKEN试验残差图

从图1可以看出全因子实验中27个主切削力响应的预测情况；14点与实际值偏差，偏差最大值接近20 MPa；BOX-BEHNKEN试验拟合误差在(-20,-10)区间上3个点，在(-10,0)区间上3个点，(0,10)区间上6个点，(10,20)区间上2个点。

正交试验残差图如图2所示。

图2 正交试验残差图

从图2可以看出全因子实验中27个主切削力响应的预测情况；17点与实际值偏差，偏差最大值接近20 MPa；正交试验拟合误差在(-20,-10)区间上4个点，(-10,0)区间上5个点，(0,10)区间上9个点。

优化拉丁超立方试验残差图如图3所示。

图3 优化拉丁超立方试验残差图

从图3可以看出全因子实验中27个主切削力响应的预测情况；19与实际值偏差,偏差最大值接近40 MPa；优化拉丁超立方试验拟合误差在(-40,-20)区间上1个点，(-20,-10)区间上6个点，(-10,0)区间上4个点，(0,10)区间上5个点，(10,20)区间上1个点，(20,30)区间上2个点。

全因子试验残差图如图4所示。

图4 全因子试验残差图

从图4可以看出全因子实验中27个主切削力响应的预测情况；9点与实际值偏差，偏差值均小于1。

综合来看，从残差的正态分布全因子试验最好，次之是正交试验，其次BOX-BEHNKEN；从3.1中的基于不同试验设计的主切削预测模型R2、RSME指标情况来看，正交试验方法的效果最好；综合残差图的偏差、残差的正态分布、R2和RSME指标情况来看全因子试验最好，次之是正交试验，其次是BOX-BEHNKEN，效果最差的是优化拉丁超立方试验。但是全因子试验需要对所在可能的试验进行全面试验，加大了试验成本，效率不高；综合判断正交试验的效果相对而言更好。

4 基于QPSO算法的预测模型改进及仿真

4.1 预测模型改进

标准粒子群算法粒子的速度和位置更新公式为：

Vi,j(t+1)=w(t)Vi,j(t)+c1r1[Pi,j(t)-Xi,j(t)]+
c2r2[Pg,j(t)-Xi,j(t)]

(9)

Xi,j(t+1)=Xi,j(t)+Vi,j(t+1)

(10)

式中：*i,j(t)—第t次迭代粒子i第j维*分量,*=V,P,X；Vi,j一般在限制在[Xmin,Xmax]；c1,c2—加速度常数，用于调整学习步长；r1,r2—[0,1]之间的随机数。

pi,j(t)=φi,j(t)Pi,j(t)+(1-φi,j(t))Pg,j(t)

(11)

在迭代过程中，粒子不断地靠近并最终到达点pi。因此，此时如果存在着一种势能(吸引势)在引导粒子向着pi点靠近，就能保证了整个粒子群体的聚集性，而不会趋向无穷大。

具有量子行为的粒子群算法的位置更新方程表达式为：

(12)

笔者采用Li,j(t)=2α|Cj(t)-Xi,j(t)|，则QPSO方程可转换为：

Xi,j(t+1)=pi,j(t)±a|Cj(t)-Xi,j(t)|
ln(1/ui,j(t)),ui,j(t)～U(0,1)

(13)

pi,j(t)=Pg,j(t)+φi,j(t)[Pi,j(t)-Pg,j(t)]

(14)

Cj(t)=

(15)

式中：a—扩张—收缩因子。

笔者采用QPSO算法对其变异函数参数进行优化,以提高其拟合精度。

基于QPSO算法的kriging预测模型改进流程如图5所示。

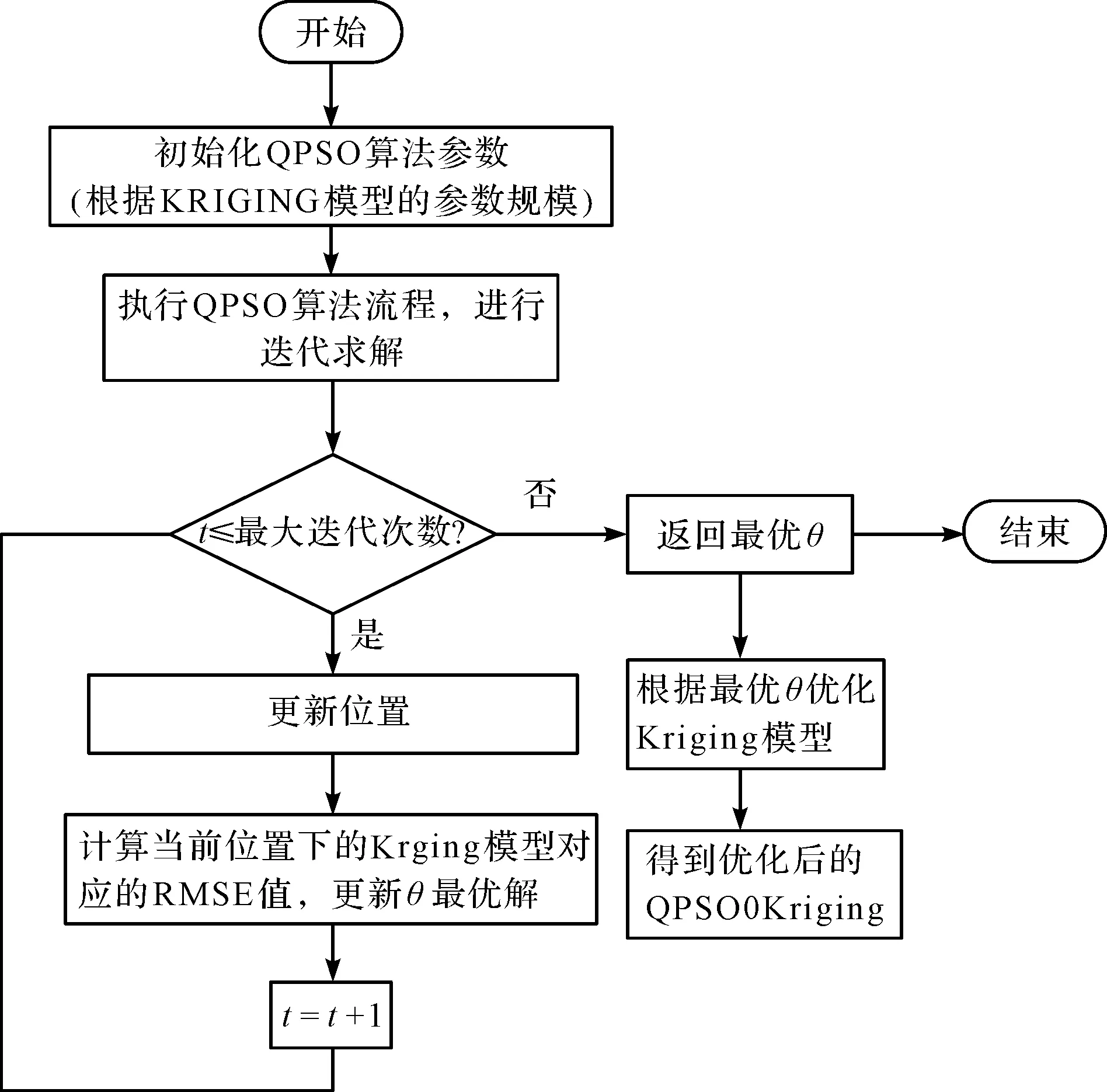
图5 基于QPSO算法的Kriging预测模型改进流程

4.2 仿真与分析

利用4.1中的QPSO-Kriging模型算法，采用正交试验结果，基于MATLAB仿真平台建立优化后的QPSO3KRIGING模型，可得到其优化前后的R2、RMSE、RMAE的结果。

优化前后主切削力Kriging预测模型指标情况如表7所示。

根据表7中的优化前后主切削预测模型指标情况可以看出，采用QPSO算法对Kriging算法进行优化后，确定性系数(R2)、均方根误差(RMSE)和相对最大绝对值误差(RMAE)都得到了一定的改善。其中，确定性系数(R2)提升0.231 6%，均方根误差(RMSE)降低17.449%，相对最大绝对值误差(RMAE)降低27.400%，优化后的Kriging模型的全局拟合精度和拟合精度都得到了提高。

表7 优化前后主切削力Kriging预测模型指标情况

基于MATLAB仿真平台建立优化后的QPSO-Kriging模型，QPSO-Kriging模型建模残差图如图6所示。

图6 QPSO-Kriging模型建模残差图

图6中，与图3相比较，从残差的正态分布和残差大小来看，优化前的Kriging算法误差分布在(-20,-10)区间上4个点，(-10,0)区间上5个点，(0,10)区间上9个点；优化后的Kriging算法误差分布在(-15,-10)区间上3个点，(-10,0)区间上7个点，(0,10)区间上8个点；优化前的误差范围在(-20，10)，优化后的误差范围在(-15，10)。由此可见，误差范围得到了进一步的缩小，提高了其精度。

5 工艺参数分析

根据建立的数学模型，笔者分析钛合金切削加工过程中切削速度、进给量以及刀具前角3个参数对切削力的影响。

加工工艺参数对切削力的影响如图7所示。

图7 加工工艺参数对切削力的影响

由图7可以看出：切削速度的增大，钛合金切削力的由大变小，呈下降趋势；随着刀具前角、进给量的增大则钛合金切削力的由小变大。

加工工艺参数交叉变化对切削力影响的等高线图如图8所示。

图8 加工工艺参数交叉变化对切削力影响的等高线图

从图8可以看出：切削速度、进给量以及刀具前角3个参数两两交叉变化时，没有引起响应面的急剧变化和突变，进给量-切削速度、进给量-刀具前角引起主切削力变化范围增大。

6 结束语

针对钛合金材料在加工过程中加工参数选择不合理导致的变形问题，笔者研究了不同样本数据建立Kriging模型的精度问题；同时采用量子粒子群算法，对传统的Kriging的变异函数参数进行了优化。

研究结果表明：

(1)利用同一工况下取得的不同切削参数的分析结果，采用BOX-BEHNKEN试验、正交试验、优化拉丁超立方试验、全因子试验4种试验设计方法下建立的kriging代理模型，R2、RMAE、RMSE 3个评价指标，全因子试验最优，其次是正交实验。但是全因子试验需要对所在可能的试验进行全面试验，加大了试验成本，效率不高；综合判断正交试验的效果相对而言更好；

(2)采用QPSO算法对Kriging算法进行优化后，确定性系数(R2)提升了0.231 6%，均方根误差(RMSE)降低了17.449%，相对最大绝对值误差(RMAE)降低了27.400%；

(3)优化前的误差范围在(-20，10)，优化后的误差范围在(-15，10)，误差范围得到了进一步的缩小，提高了其精度，为钛合金切削加工参数优化问题提精度更高的数学模型；

(4)随着切削速度的增大，钛合金切削力由大变小，呈下降趋势；随着刀具前角、进给量的增大则钛合金切削力的由小变大。切削速度、进给量以及刀具前角3个参数两两交叉变化时，没有引起响应面的急剧变化和突变，进给量-切削速度、进给量-刀具前角引起主切削力变化范围增大。