γ辐照加工用新型工作模体设计研究

杨 磊，刘 燕，周毅吉，李文革，张美琴

(1.烟台大学，山东 烟台 264005；2.湖南农科院，湖南 长沙 410300)

γ辐照装置辐射场的均匀度和稳定度是确保辐照工艺精确制定和有效执行的基础和关键，其受装置辐射源部署结果、生产线机械结构及运动方式、货物材料密度及堆码方式等多种因素的影响。国内γ辐照装置多为通用装置，加工货物种类和剂量要求差别明显，需经常对装置辐射场和货物剂量场进行测量，标准方法是构建等效剂量模体并内置标准剂量计，经照射后测量得到有关分布。剂量模体分为标准模体和工作模体，前者多用于行业评价和同行比对，后者主要用于日常工作，需灵活多变。工作模体外形尺寸多以装置自带货箱为准，模体填料相关标准建议为水[1]，但因部分装置货箱密封性、生产线承重能力、货物密度差异等原因其在日常应用中偏少，部分公司以瓦楞纸板为填充物，密度达0.1 g/cm3，模拟范围相对不足[2]，也有部分公司采用锯末、泡沫、水泥以不同比例掺混作为填料[3]，在现场卸装、货物空隙率模拟等方面存在改进空间。总体来看，国内外对工作模体的需求多但公开研究少，已有模体需改进和完善，为此有必要研究设计新型剂量模体，达成扩展货物材料和密度比对范围、现场应用更简单干净、与模拟计算模型匹配程度更好等目的。

本文介绍工作模体结构和填料的新型设计方法，采用蒙特卡罗方法、随机填充方法(RCS)建模实际γ辐照装置及新型工作模体，研究分析模体关于填料密度、孔隙率、填充方式等主要影响因素的分布规律并给出优化方案。

1 新型工作模体的基本设计

1.1 模体的结构设计

为兼顾国标要求[4-5]，新型工作模体的基本结构如图1所示。模体直接以辐照装置货箱为外壳，内置上下两块由铝或聚丙烯等耐辐照材料制作的长方形顶板(底板)和若干数量的剂量计套管[3]，顶(底)板尺寸较货箱稍小，以便装卸。顶(底)板上的开口用于模体填料的装载和卸载，板上另外安装有均匀密布的短螺纹铝制支杆以便灵活套接不同数量的套管，从而可满足xy平面方向剂量场测量精度的需求。套管内交替布置剂量计和聚丙烯泡沫垫块，调整垫块长度可满足z轴向剂量场测量精度的需求。

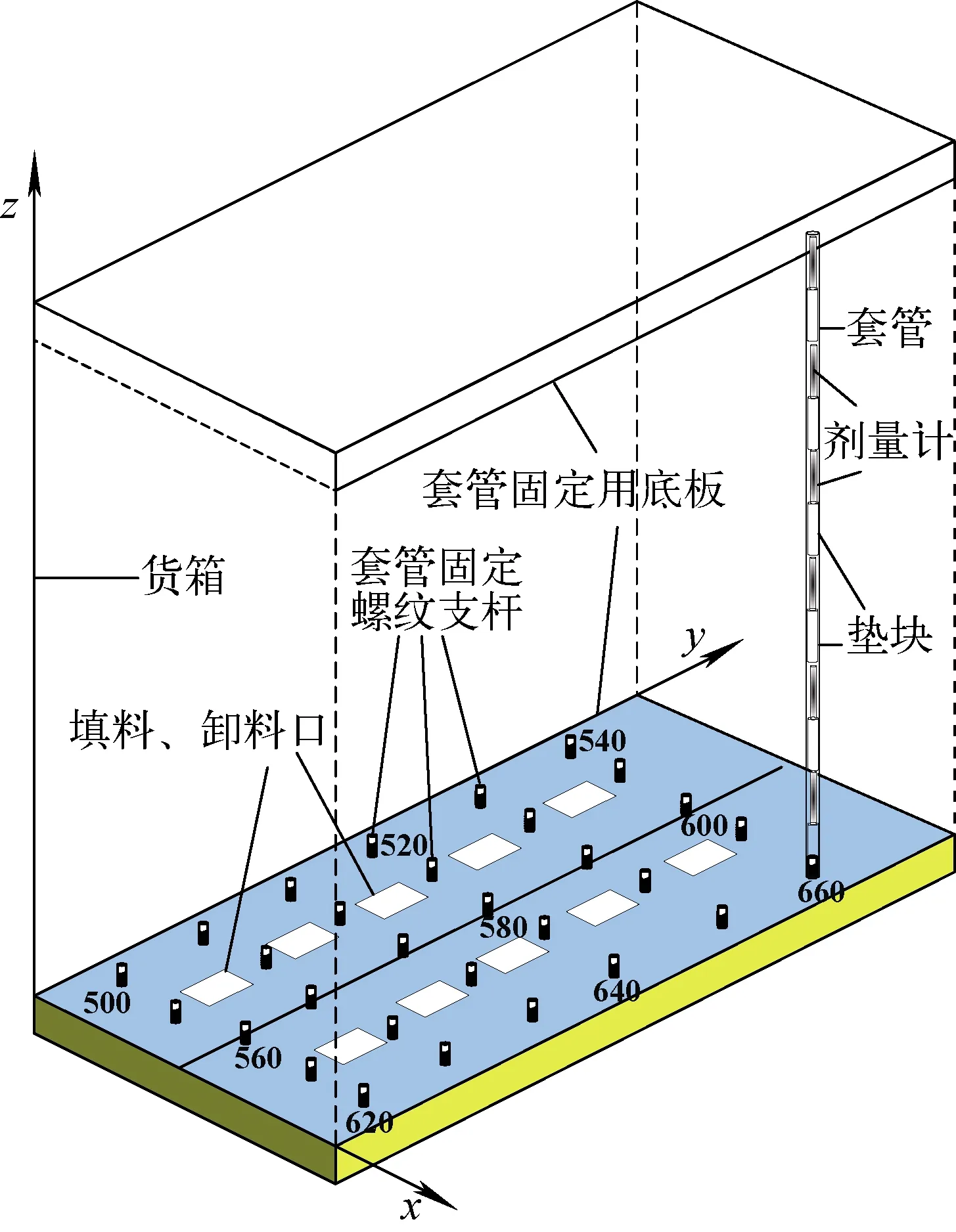
图1 新型工作模体的基本结构Fig.1 Basic structure of new operating phantom

1.2 模体的填料设计

理论上模体填料应采用货物等效材料，但实际操作困难，多年来业界针对主要货物的材料和密度，基于经验多采用瓦楞纸、木屑、泡沫、秸秆碎块、混凝土颗粒及其混合物等作为模体填料，具有等效性好、来源广泛、价格低廉等优点，但也存在现场布置较为复杂，不够灵活和清洁等缺点，同时混合填料的成分较难精确获取，与理论建模及优化设计结果比对较为困难。本文采用聚丙烯制作的实心和空心(可内置其他等效材料)小球作为填料[6]，在保持已有优点、克服上述困难的同时，还可模拟已有类型模体未关注的货物间隙效应。

2 模体优化设计用辐照装置理论建模

本文采用蒙特卡罗工具开展模拟计算，该方法在粒子输运计算领域应用广泛，计算结果的精确度和可靠性得到公认[7-9]。基于某γ辐照装置某次实际排源结果精细构造辐射场[10]，源棒及空间位置、护源板等装置核心组件均取自实际参数，源棒主要考虑了源芯块、不锈钢外壳和端塞，共建模44根源棒，为模拟货箱(模体)双面照射效果，实际对称建模88根源棒[11-12]。货箱内置模体尺寸为60 cm×70 cm×136 cm，未考虑货箱壁；箱内均匀布置9根铝制套管，位置如图1中500～660等数字所示，套管壁厚为3.0 mm、内表面半径为0.5 cm、高度为136 cm；每根套管内置10个水剂量计，其高为4.0 cm、半径为0.4 cm，所有套管内置剂量计编号分别为501～510、521～530、541～550、561～570、581～590、601～610、621～630、641～650、661～670，共90个剂量计。货箱几何中心点与源架几何中心点对齐，货箱内填充聚丙烯小球作为模体填料(图2)。

为兼顾计算效率和精度，货箱外空气区域仅考虑光子输运，货箱内部区域采用光子-电子联合输运模型。γ光子的能量设置为1.17 MeV和1.33 MeV并等概率抽样；以最大活度源棒为基准对其他源棒活度进行归一化处理以确定不同源棒的抽样概率；单根源棒在芯块区进行空间均匀抽样。光子和电子的能量截断值均为默认的1 keV，采用*F6记录沉积在剂量计中的射线能量，抽样次数为5×107。辐照装置的粒子输运过程检验结果如图3所示。

为进一步验证辐照装置剂量计算的准确性，以文献[10]的工作为基础，在源架几何中心垂线上等距离(20 cm)布放9个直径为1 cm的充水小球，在间距为80 cm的镜像源架面的对角线上均匀布放8个充水小球。利用*F6计算小球中沉积能量(剂量)，所有结果最大计算相对不确定度为4.873 5%，结果具有统计意义，与文献[13]中标准理论公式的剂量计算结果进行比较得到相对偏差(表1)。由表1可知，蒙特卡罗模拟结果与理论计算结果的相对偏差在5%以内，满足工程计算精度需要，由此可确定当前建模γ辐照装置的辐射场、新型工作模体的有效性和可靠性。

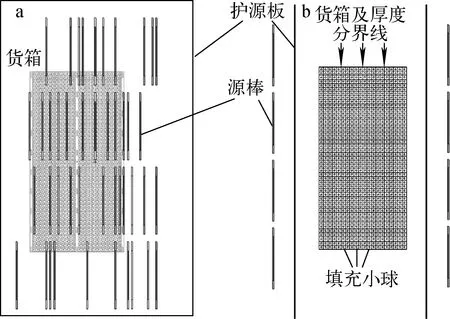
a——正视图(货箱隐蔽)；b——侧视图(部分源棒隐蔽)图2 γ辐照装置和货箱的几何建模Fig.2 Geometric modeling of gamma irradiator and container

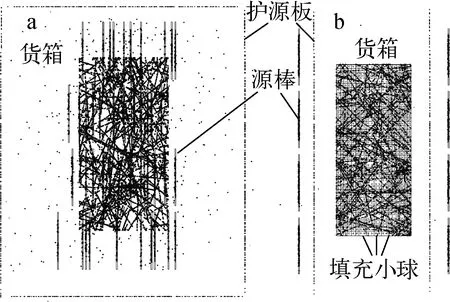
a——正视图(货箱隐蔽)；b——侧视图(部分源棒隐蔽)图3 辐照装置的粒子输运过程检验结果Fig.3 Inspection result of particle transport process in irradiator

3 新型工作模体参数优化设计

3.1 套管材料及壁厚的优化设计

套管是保证剂量计在货箱内均匀布置及避免机械损坏的关键部件，在辐照模型中精细构建了相关结构，图4为套管与管内剂量计的空间结构示意图。

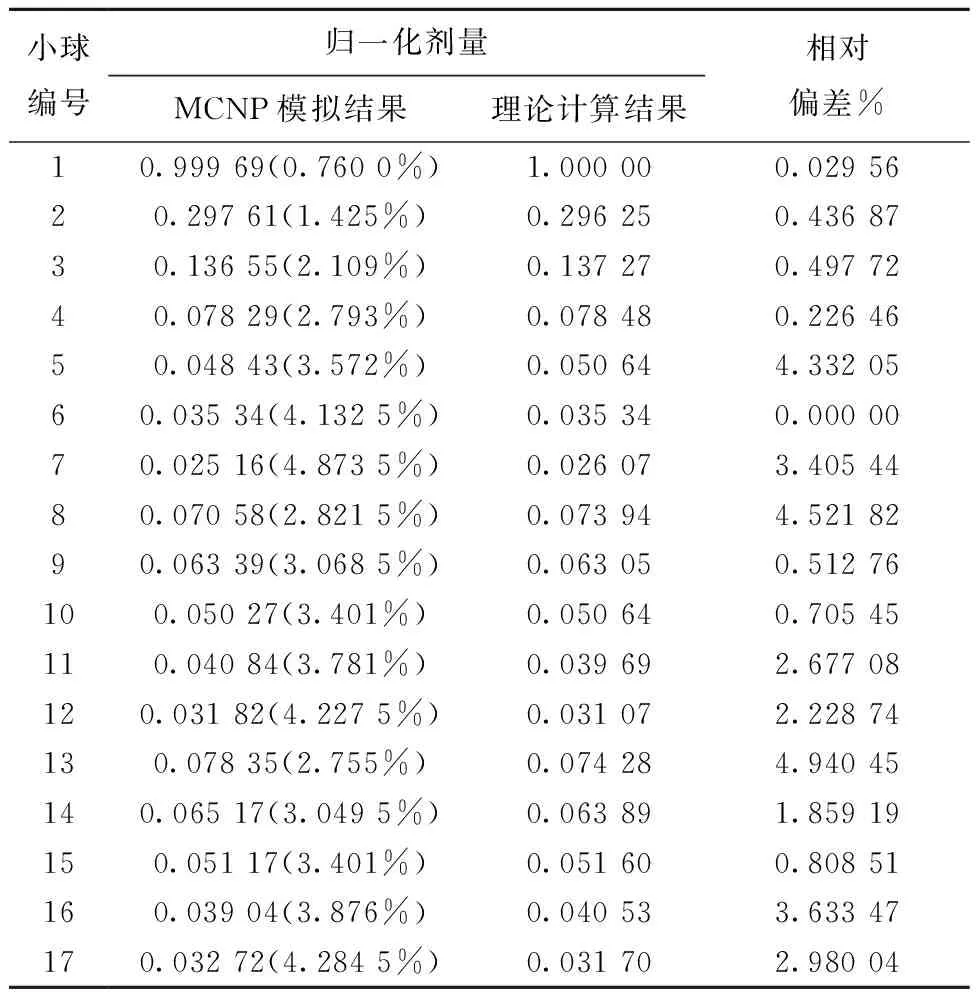
表1 剂量验证的理论方法和蒙特卡罗方法计算结果Table 1 Result of theoretical method andMonte Carlo method to dose validation

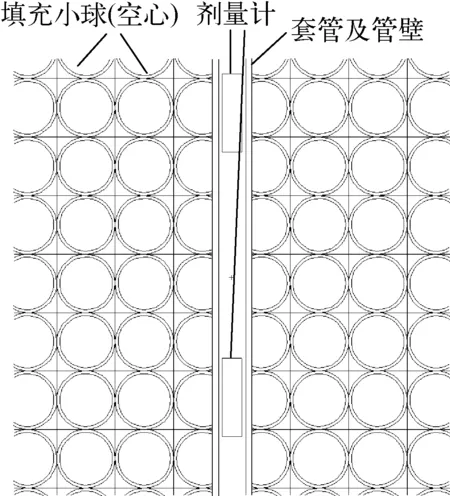
图4 套管与管内剂量计的空间结构示意图Fig.4 Spatial structure scheme of sleeve and dosimeter

套管需用具有足够机械强度的材料制成，但其存在会干扰辐射场并造成剂量计测量结果出现偏离，本工作分别计算了铝和铁制套管材料外径统一为20.0 mm，管壁厚分别为2.0、3.0、4.0、5.0 mm情况下及无管壁情况下的模体剂量分布，得到9组共810个结果，所有结果最大计算相对不确定度为4.46%，结果具有统计意义。分别计算无管壁和8组有管壁情况下剂量的相对偏差，选出其中最大值列于表2，由此评估剂量计套管对剂量场的干扰影响程度。

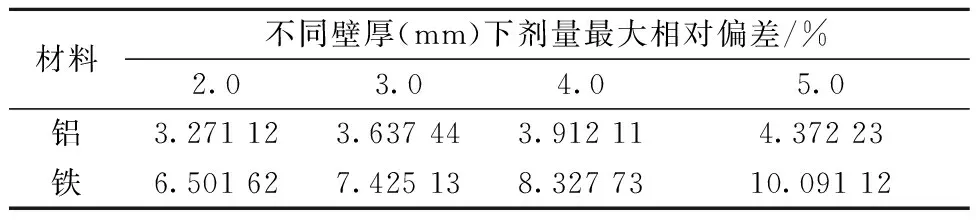
表2 不同材料和壁厚套管对模体剂量场造成的剂量最大相对偏差Table 2 Dose maximum relative deviation of phantom dose field caused by sleeves with different wall thicknesses and materials

从表2可知，在满足机械强度要求的前提下，套管应尽量采用薄壁及低原子序数材料。为进一步分析剂量场干扰影响的空间分布规律，分别选择最佳壁厚为3.0 mm的铝管和壁厚为2.0 mm的铁管对应的90个剂量相对偏差绘图，结果如图5所示。可看出，铝制套管造成的剂量相对偏差最大不超过3.637 44%，且对剂量场的干扰整体较小。铁制套管对剂量场的干扰影响相比明显增大，特别是编号为541、562等剂量计位于货箱端角，离源棒距离较远，光子穿过铁的路径较长，部分光子散射严重，对剂量场的干扰更加严重。由此可确认套管材料应优先选择镁铝、铝锂合金，并可推断机械性能强、耐辐照、不含高原子序数成分的塑料也合适。

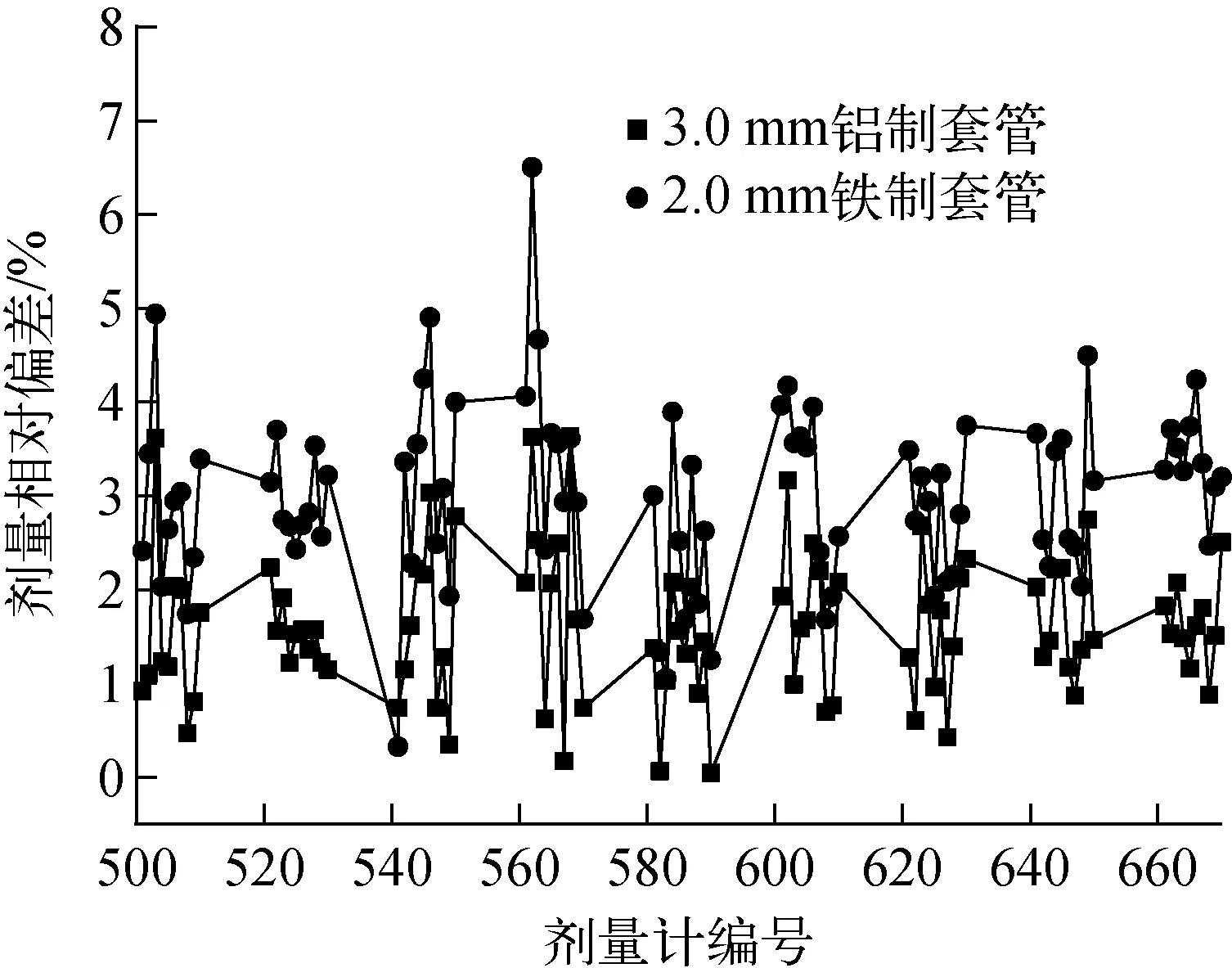
图5 不同材料和壁厚套管对剂量场的干扰影响的空间分布Fig.5 Spatial distribution of dose field interference result caused by sleeves with different wall thicknesses and materials

3.2 填料小球半径的优化设计

填料是工作模体设计的重点，相比传统均匀填充方式，当前工作综合考虑价格、市场供应能力及模拟真实货物孔隙等因素，选择半径为0.5、1.0、2.0、3.0、4.0、5.0 cm共6种聚丙烯小球作为模体填料，堆积方式采用立方均匀方式，球体立方堆积方法的最高填充比为0.523 6[14]，能涵盖常见货物的等效密度范围；作为比对，本工作另外计算了各等效密度聚丙烯均匀填充货箱情况下的剂量分布情况，得到12组共1 080个结果，所有结果的最大计算相对不确定度为4.93%，结果具有统计意义。分别计算6种小球填充和对应等效均匀填充情况下剂量相对偏差，选择其中最大值列于表3，由此评估填料小球半径对剂量场的干扰影响。由表3可知，小球半径越大，孔隙率越大，对应等效密度缓慢降低，剂量相对偏差增大明显，这表明填料尺寸的影响不能忽视，在工程上采用均匀填料来比对和评估有空隙货物剂量的做法有待进一步改进。为进一步分析剂量场干扰影响的空间分布规律，对6组对比算例的剂量相对偏差绘图，结果如图6所示。可看出，位于模体中心平面上编号为561～570、601～610两组剂量计值的相对偏差最大，主要原因是该区域光子和次级电子的散射最为严重且双面照射，使得剂量偏差更为明显。因货箱结构改善可能性较小，为保证测量精确度，建议以货箱1/4厚度为分界线(图2b)，提高内侧区域剂量计的布放密度。

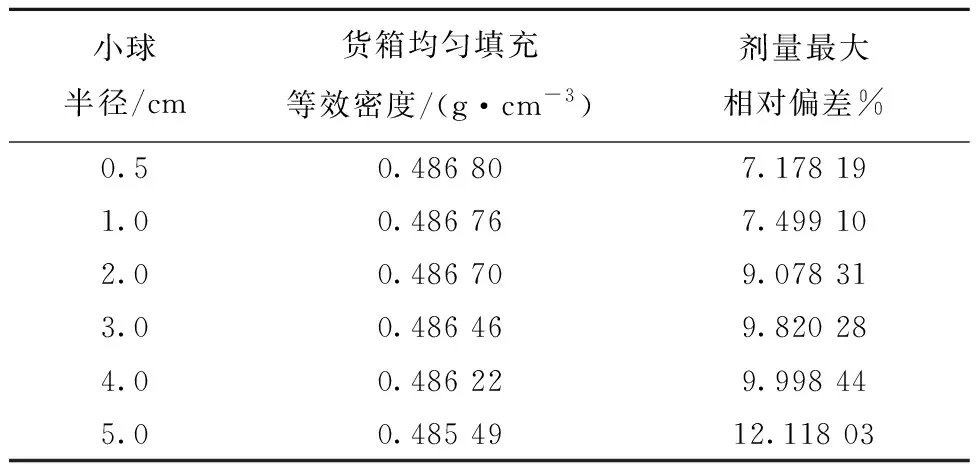
表3 不同尺寸填料小球对模体剂量场造成的剂量最大相对偏差Table 3 Dose maximum relative deviation of phantom dose field caused by different size filling balls

3.3 填料小球密度涵盖范围的优化设计

常见货物的平均密度主要集中在0.1～0.5 g·cm-3，从表3可知实心小球涵盖的货物密度范围偏窄，本文选择外部半径为3.0 cm的空心小球作为货箱填料，通过改变其空心半径(壁厚)以改变填料等效密度，共计算0.1、0.2、0.3、0.4、0.45、0.48 g·cm-36种情况及对应等效密度均匀填充情况，获得12组1 080个计算结果，将空心小球填充组的最大计算相对不确定度、小球填充和等效均匀填充的剂量场剂量最大相对偏差列于表4，由此评估空心填充对剂量场的干扰影响程度。由最大计算相对不确定度可知结果具有统计意义，由剂量最大相对偏差可知空心填充对剂量场影响较小，工程应用上可行，可采用壁厚为1.0、2.5、4.0、6.5、8.5、11.5 mm的小球替代。

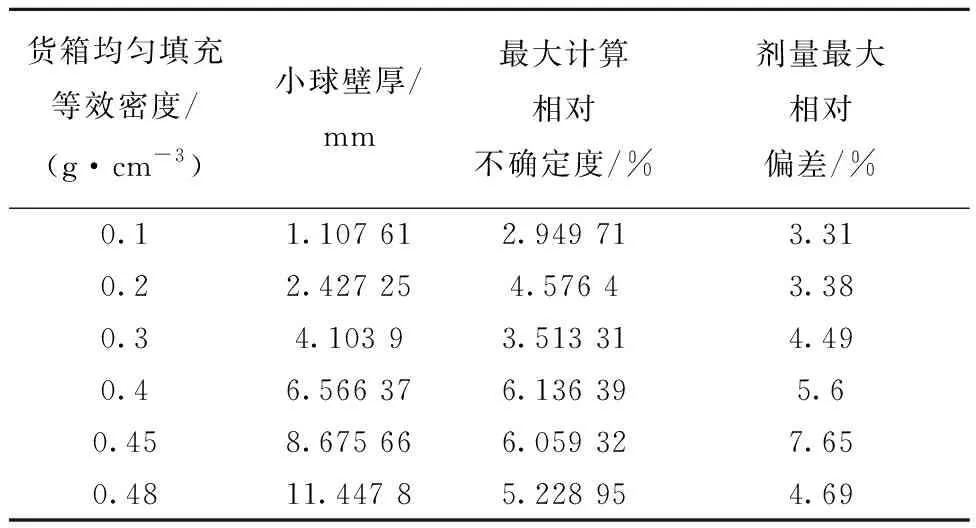
表4 不同壁厚空心小球对模体剂量场造成的剂量最大相对偏差Table 4 Dose maximum relative deviation of phantom dose field caused by different wall thickness hollow balls

3.4 小球填充方式的优化设计

考虑到实际工程实施很难做到小球的理想立方填充，需进一步计算和分析随机填充方式条件下剂量模体受到的干扰影响程度。本文基于RCS模拟小球在货箱内的随机填充，该方法最大填充比为0.1～0.65[15]，可覆盖常见的货物密度范围。

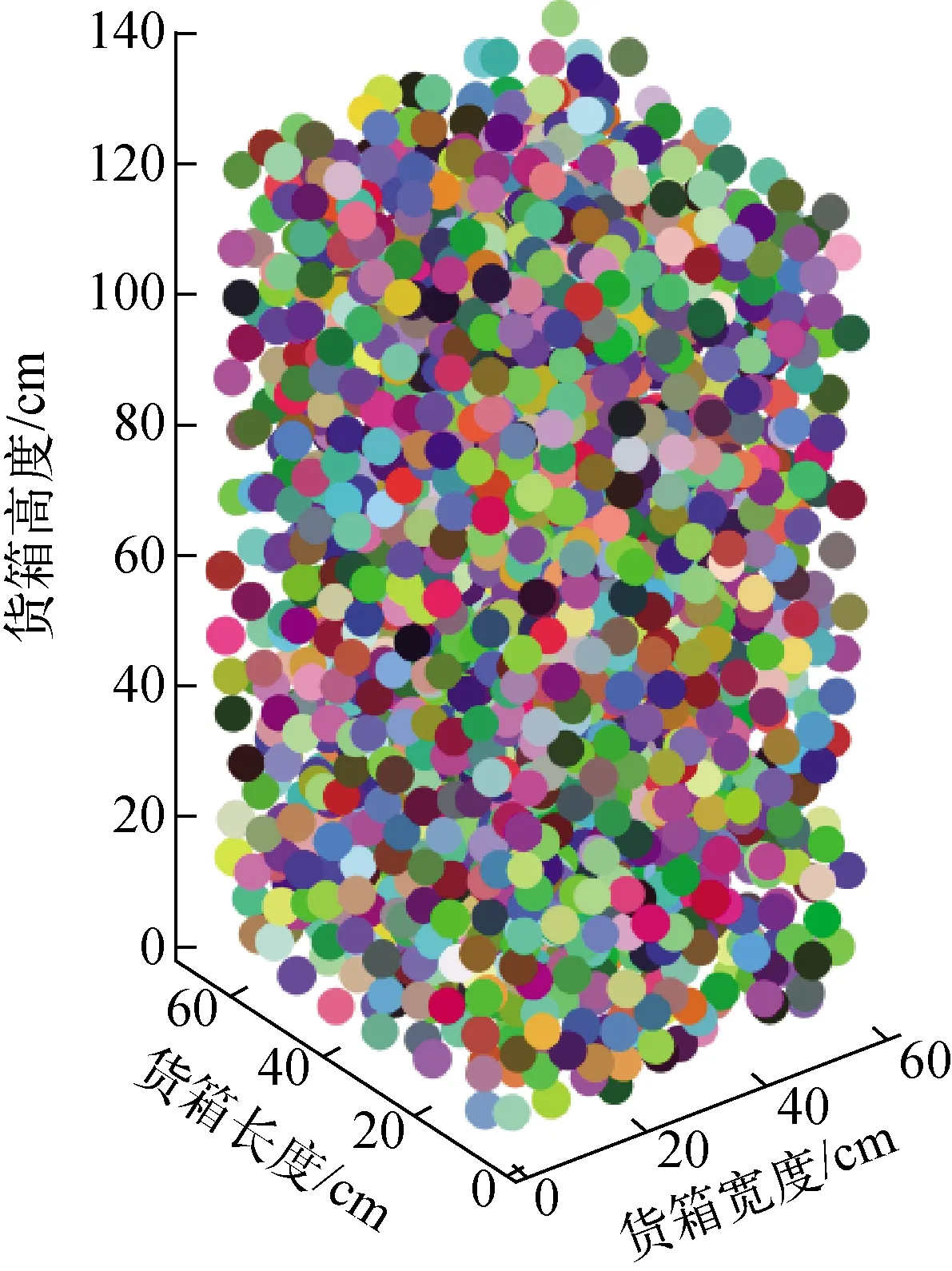
图7 小球在模体(货箱)中的随机填充结果Fig.7 Random filling result of filling ball in phantom (container)

计算过程中设定小球半径固定，为刚体，不考虑滑动摩擦系数，迭代填充500次以模拟货箱震动过程直至填满为止[16-17]，具体计算了半径为1.0、2.0、3.0、4.0 cm 4类小球的填充过程，求解得到小球在货箱内的空间位置，进而与辐照装置模型合并构建全范围真实计算模型，图7为小球在模体(货箱)中的随机填充结果，图8为随机填充模式下的辐照装置的粒子输运过程检验结果。从图7、8可知，联合采用RCS和蒙特卡罗方法进行全范围真实模型构建及剂量计算是可行的，进一步计算剂量分布，共获得8组720个结果。小球半径、货箱等效填充密度、小球填充等最大计算相对不确定度、小球填充和等效均匀填充条件下剂量场剂量最大相对偏差列于表5。由表5可知，随机填充与立方填充结果处于同一水平，进一步表明联合方法进行剂量计算是可靠有效的，另外随机填充模式下剂量最大相对偏差普遍较立方填充的大，主要原因是前者模体小球的空间布放相比不够均匀，光子电子散射更复杂，同时抽样次数为5×107次不变导致计算相对不确定度增加也是因素之一。另外从等效密度可知当前RCS求解能力不足，后续将采用如DEM方法[18]提升填充比以涵盖更宽的模拟密度范围。

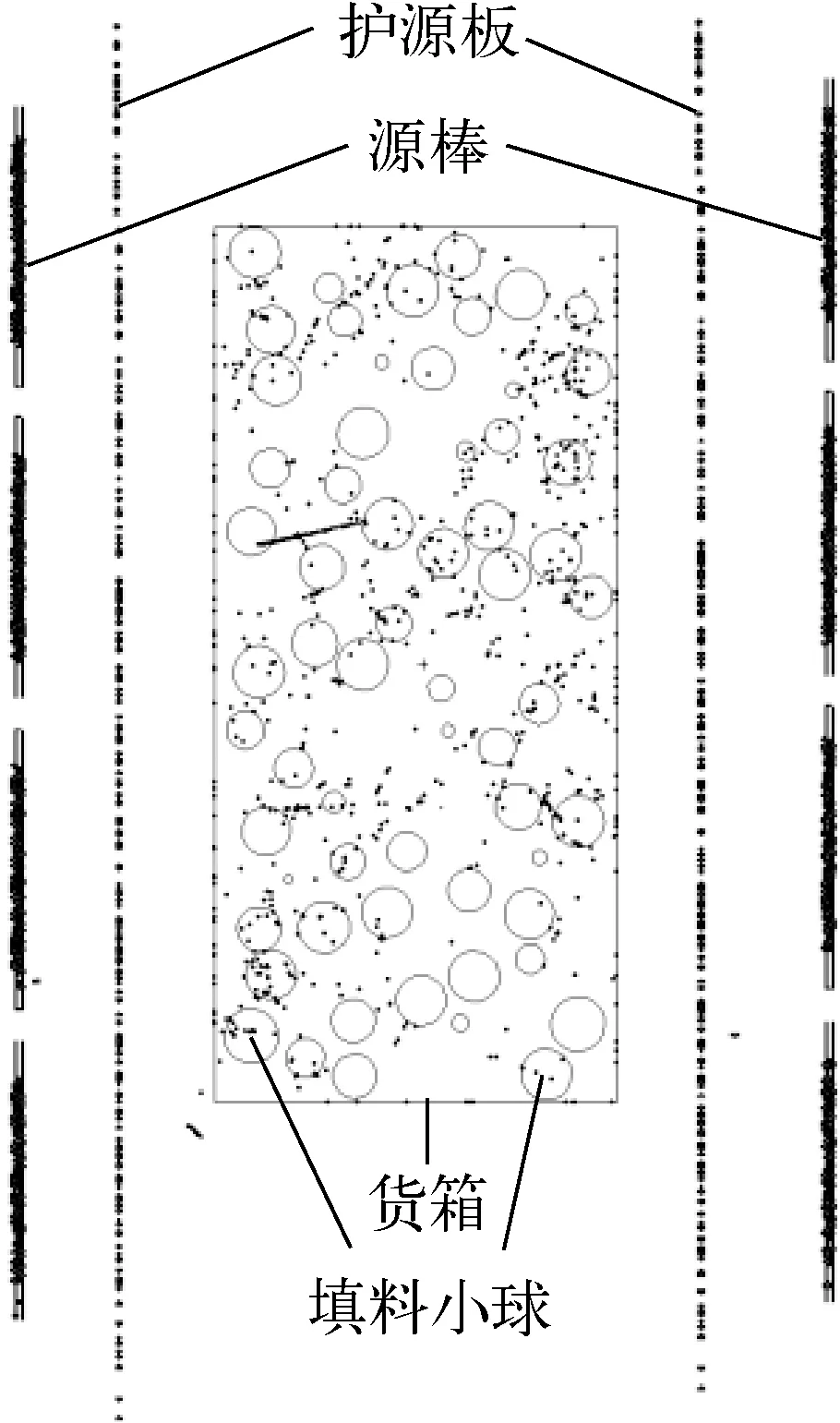
图8 随机填充模式下的辐照装置的粒子输运过程检验结果Fig.8 Inspection result of particle transport process of irradiator in random filling mode

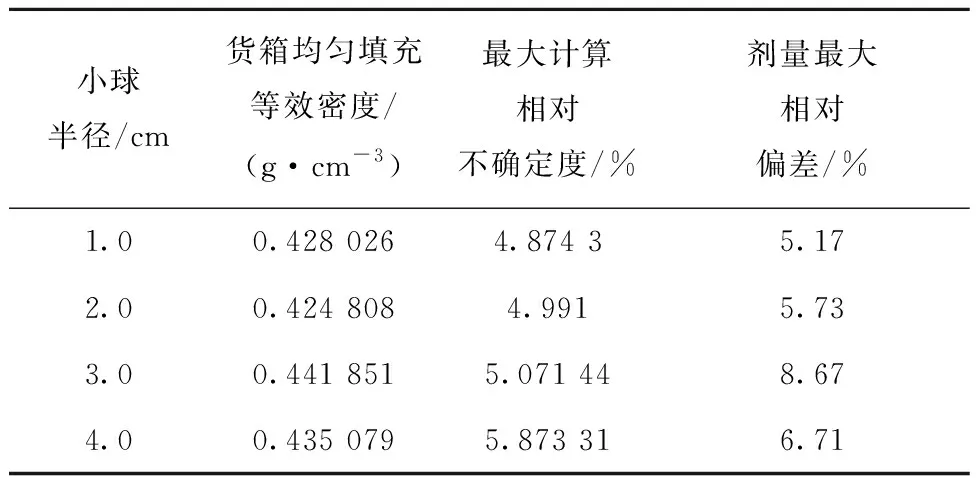
表5 随机填充模式下不同尺寸填料小球对模体剂量场造成的剂量最大相对偏差Table 5 Dose maximum relative deviation of phantom dose field caused by different size filling balls under random filling mode

4 结论

本文研究设计了一种用于获取γ辐照装置辐射场和货物剂量场真实分布的新型工作模体，基于真实γ辐照装置参数构建了有效可用的模拟辐射场，针对模体剂量计套管材料与壁厚、填料小球尺寸、空心填料小球尺寸与壁厚、小球填充方式等进行了优化设计计算。结果表明，新型工作模体贴近工程实际需要、设计可行性好、材料来源广泛、价格低廉、兼顾参数多且量程更宽、现场布置和卸载更简便清洁，具备推广应用的潜力。