基于染色体畸变的细胞存活模型研究

王文静，李春艳，邱 睿，武 祯，张 辉，李君利

(1.中国原子能工业有限公司，北京 100032；2.清华大学 工程物理系，北京 100084；3.同方威视技术股份有限公司，北京 100084；4.清华大学 粒子技术与辐射成像教育部重点实验室，北京 100084)

质子和重离子先进放疗技术在放射治疗中的应用越来越广泛[1]。与传统放疗相比，质子和重离子放疗成本较高，但随着精准和个体化医疗概念[2]的提出，以及束流扫描技术的引入，质子和重离子放疗在物理和生物方面的优势更加突出。物理方面，质子和重离子剂量深度分布存在布拉格峰，布拉格峰末端剂量迅速下降；生物方面，重离子有增强的生物效应等优点[3]。但与此同时也带来了如何准确评估质子和重离子生物效应的挑战[4]。

目前已有许多研究辐射致死效应的体外实验。为预测辐射沉积能量与所致细胞死亡效应之间的关系，基于放射生物学实验，国际上建立了不同的细胞存活模型，包括现象性模型和机理性模型[5]。现象性模型包括靶学说、线性平方(LQ)模型等。根据生物效应，机理性模型分为基于DNA损伤的细胞存活模型和基于染色体畸变的细胞存活模型。国际上，基于DNA损伤的细胞存活模型以Stewart等[6]提出的修复-错误修复-固定(RMF)模型为代表，基于染色体畸变的细胞存活模型以Ballarini等[7-9]提出的细胞死亡和染色体畸变生物物理分析(BIANCA)模型为代表。此外，McMahon等[10-11]针对细胞周期的不同阶段，分别提出了基于DNA损伤和基于染色体畸变的细胞存活模型。 RMF模型将快速蒙特卡罗损伤模拟程序(MCDS)估计的双链断裂(DSB)产额作为模型的输入参数，用于生物学参数α与β的计算，尽管一定程度上体现了辐射致细胞生物效应的机制，但用RMF模型计算的β参数随传能线密度(LET)是单调增加的，而根据细胞存活实验得到的β参数随LET有明显的递减趋势。McMahon等在计算辐射所致DNA损伤时，不同粒子类型单位剂量的DSB产额采用与光子相同的值，合理性存在疑问。Ballarini等和McMahon等提出的基于染色体畸变建立的细胞存活模型，一方面对染色体畸变类型考虑的不全面，另一方面两个模型都建立在双着丝粒和染色体断片等是独立的基础上，但不同类型的染色体畸变可能是不独立的。因此，有必要建立更加合理、准确的机理性模型。

本文使用纳剂量生物物理蒙特卡罗模拟程序NASIC，模拟不同LET辐射所致细胞核内不同类型染色体畸变的产额，分析染色体畸变产额随LET变化的规律，在此基础上，建立基于染色体畸变的细胞存活机理模型。

1 NASIC程序DNA损伤修复模块开发

纳剂量生物物理蒙特卡罗模拟程序是为了模拟辐射对纳米量级的生物大分子，如DNA、染色质等产生的效应而开发的蒙特卡罗模拟程序。目前国际上典型的纳剂量生物物理蒙特卡罗模拟程序有亥姆霍兹慕尼黑-德国辐射环境健康研究中心(HMGU)的PARTRAC[12]、瑞典卡罗林斯卡学院(Karolinska Institute)开发的KURBUC[13]、欧洲核子中心(CERN)开发的GEANT4-DNA[14]、清华大学工程物理系辐射防护与环境保护研究室开发的NASIC[15]，等。其中，PARTRAC和KURBUC等仅限内部研究或合作研究时使用，GEANT4-DNA是开源的程序，但其DNA损伤修复模块正在开发中。

NASIC程序包括物理模块、前化学模块、化学模块、几何模块和DNA损伤模块[15]。NASIC几何模块建立了一个精确到DNA原子几何的、处于G1期的人体淋巴细胞的细胞核生物靶模型。该细胞核的直径约11 μm，包含46条染色质和2个核仁，总DNA含量约6.2 Gbp，具有DNA双螺旋链、核小体、染色质纤维单元、核基质结合区等一系列DNA结构。物理模块模拟辐射粒子在细胞中的输运过程；前化学模块模拟电离、激发水分子通过不同方式离解和热能化，产生多种辐解化学自由基的过程；化学模块模拟这些自由基扩散并相互发生化学反应的过程；DNA损伤模块判断和统计辐射所致DNA的直接损伤和间接损伤，获得DNA单链断裂(SSB)、双链断裂(DSB)和碱基损伤(BD)的分布信息。

为进一步模拟DNA受到辐射损伤后的修复过程，本文开发NASIC程序的DNA损伤修复模块。考虑到处于G1期的细胞对DSB的修复途径主要为非同源末端连接(NHEJ)修复，首先对DSB的NHEJ修复途径进行模拟建模，

根据修复结果，判断和统计辐射所致染色体畸变类型及产额，然后对DNA损伤修复模拟结果进行验证。

1.1 DNA损伤修复模块开发

DNA损伤修复模块对NHEJ修复的模拟可分为对DSB末端状态变化的模拟、对DSB末端空间位移的模拟和对修复结果的判断3个部分。

参考PARTRAC[16]，NASIC将DSB末端分为无余末端和带余末端2类，若距离DSB末端20个碱基对(bp)内存在BD或SSB，则判定为带余末端。对于带余末端，先逐个修复BD和SSB，最后再进行DSB修复。NASIC对无余末端和带余末端的状态改变流程的模拟示于图1，其中，无余DSB末端的状态从C1到C8，带余DSB末端的状态从D1到D8，修复过程从步骤1到步骤11。图中，每个步骤对应的数字为该步骤的状态改变时间常数，用于计算该步骤DSB末端的状态改变概率。

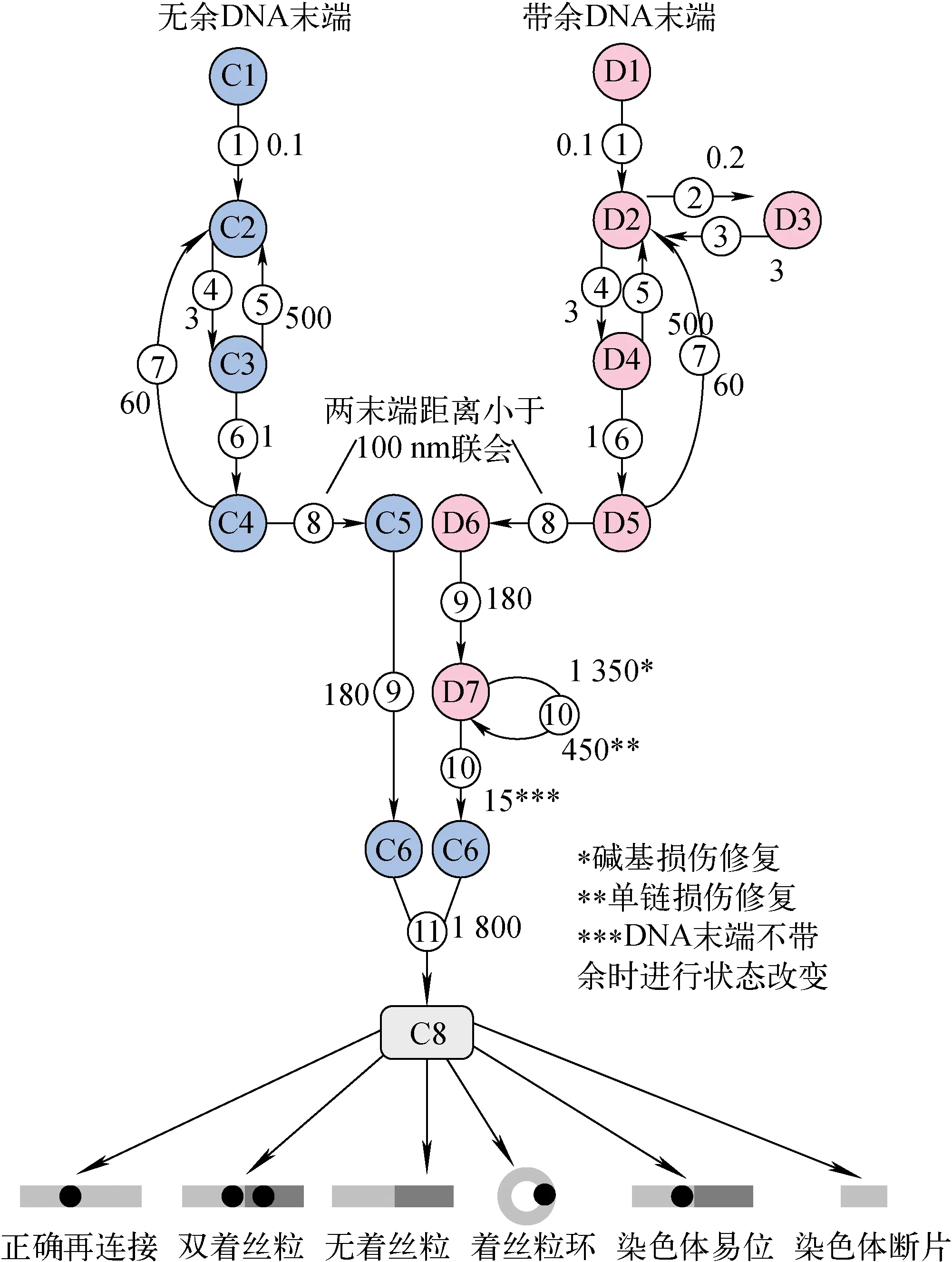
图1 DNA修复模型中无余末端和带余末端的状态改变流程Fig. 1 State change process of clean DNA end and dirty DNA end in DNA repair model

ξi=1-exp(-δt/τi)

(1)

式中：δt为时间步长，NASIC中取0.01 s，即每隔0.01 s对每个DSB末端进行1次状态改变的判断；τi为步骤i的状态改变时间常数，s；ξi为单位时间步长下任一DSB末端经历步骤i从当前状态变为下一状态的概率。

具体修复过程如下。

步骤1：DSB刚形成时，染色质纤维会进行解压缩，断点处的螺旋被打开，暴露出断裂末端，使修复酶有空间依附。

步骤2：带余末端会招募其他修复蛋白，阻断了NHEJ酶Ku70和Ku80的结合。

步骤3：这种阻断性结合会持续一段时间，然后恢复。

步骤4：Ku70和Ku80首先连接到DSB末端。

步骤5：Ku70和Ku80会有一定的可能从DSB末端脱离。

步骤6：DNA-PKcs结合到DNA的末端，与Ku70和Ku80形成DNA-PK复合物。

步骤7：DNA-PK复合物有一定的可能从DSB末端脱离，DSB末端回到没有酶连接的状态。

步骤8：两个末端距离小于100 nm时，DNA-PK复合物将两个末端连接起来，末端之间形成联会复合物。

步骤9：DNA-PK复合物交叉磷酸化，NHEJ修复酶连接并激活。

步骤10：带余末端临近的SSB和BD被逐一修复，SSB的修复概率和BD的修复概率不同；带余末端变为无余末端后，才可进行后续修复。

步骤11：2个末端再连接，1个DSB被清除。

NASIC将DSB末端的空间位移模拟为在球形空间的半自由扩散运动。球形空间的圆心为距离DSB末端最近的核基质结合区的中心。球形空间的半径为DSB末端和核基质结合区中心之间染色质纤维的长度。伴随着解螺旋过程，染色质纤维的长度会以解螺旋速度5 nm/1 000 s[17]随时间线性增加。DSB末端位移的大小采用扩散系数计算，位移的方向为各向同性。联会前扩散系数为170 nm2/s，联会后扩散系数为17 nm2/s[18]。

NHEJ修复过程结束后，对染色体畸变的类型和产额进行判断和统计。目前NASIC判断和统计的染色体畸变类型包括双着丝粒、无着丝粒、染色体易位、着丝粒环，以及>3 Mbp的染色体断片等(图1)。

1.2 DNA损伤修复模块验证

采用DNA损伤修复模块，模拟不同射线类型所致DNA损伤的修复过程。通过将修复曲线、不同类型的染色体畸变产额的模拟值与实验数据进行对比，对DNA损伤修复模型进行验证。

不同类型射线的修复曲线与实验数据的对比示于图2。由图2可看出，对于60Co γ射线[19-20]、4He离子[21]和14N离子[12]所致的DNA损伤，NASIC模拟的未修复DSB末端比例随时间的变化趋势均与实验数据符合得很好。

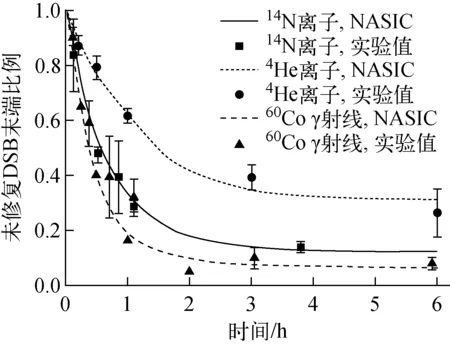
图2 不同类型射线所致DNA损伤的修复曲线与实验数据的比较Fig.2 Comparison between modelled repair curves and experimental data of DNA damage induced by different types of particles

60Co γ射线[22]和238Pu α粒子[23]所致不同类型染色体畸变产额的模拟值与实验数据的对比示于图3，其中，可见畸变包括双着丝粒、无着丝粒、着丝粒环，以及>3 Mbp的染色体断片。由图3可看出，NASIC能较好地模拟不同类型射线所致不同类型染色体畸变的产额。

2 辐射所致染色体畸变产额的规律

采用NASIC模拟统计不同剂量60Co γ射线和不同LET质子照射所致不同类型染色体畸变的产额，分析不同类型染色体畸变产额之间的关系、染色体畸变产额随受照剂量的变化规律，以及相同剂量下染色体畸变产额与射线LET的关系。

2.1 不同类型染色体畸变产额之间的关系

不同类型染色体畸变产额(本文均指单个细胞的产额)之间的关系如图4所示。从图4a可见，双着丝粒产额和无着丝粒产额、染色体易位产额都存在显著的线性关系：对于无着丝粒，相关系数R2=0.996 4；对于染色体易位，R2=0.997 0。从图4b可见，尽管着丝粒环的产额很小，与>3 Mbp的染色体断片产额存在量级上的差异，因此不确定度较大，但着丝粒环产额与>3 Mbp的染色体断片产额也存在线性关系，R2=0.973 9。

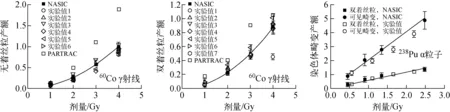
图3 辐射所致染色体畸变产额的模拟值与实验数据的比较Fig.3 Comparison between modelled values and experimental date of radiation-induced chromosome aberration yield

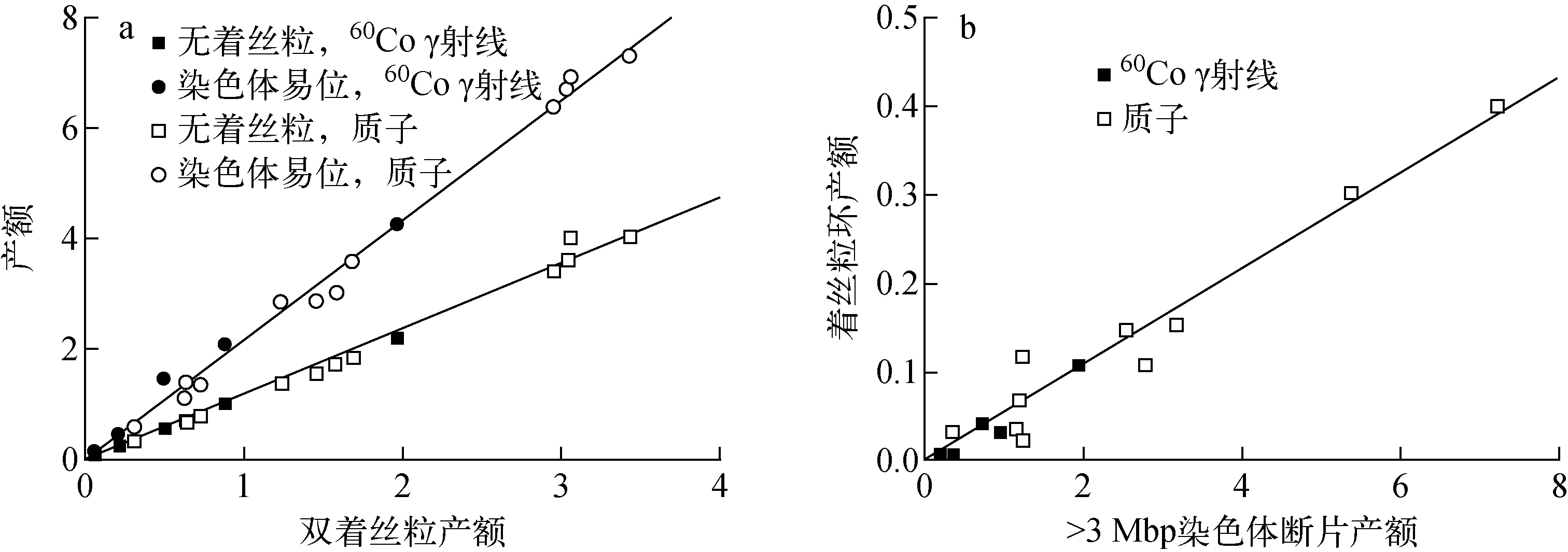
图4 不同类型染色体畸变产额之间的关系Fig.4 Relationship among different types of chromosome aberration yield

2.2 染色体畸变产额的剂量-效应关系

由于在染色体畸变类型中，双着丝粒和无着丝粒、染色体易位有显著的线性关系，着丝粒环与>3 Mbp的染色体断片有明显的线性关系，所以，在分析染色体畸变产额的剂量-效应关系时，只需要分析双着丝粒和>3 Mbp的染色体断片的剂量-效应关系。

60Co γ射线和不同LET质子照射下，双着丝粒和>3 Mbp的染色体断片的产额随细胞受照剂量的变化示于图5。由图5可看出，当细胞受到光子或较低LET射线照射时，双着丝粒产额与细胞受照剂量呈线性平方关系；随着射线LET的增大，双着丝粒产额与细胞受照剂量呈线性变化趋势。对于60Co γ射线和LET在27.6 keV/μm以下的质子，>3 Mbp的染色体断片产额与细胞受照剂量呈线性平方关系。

2.3 染色体畸变产额随LET变化规律

辐照剂量为2 Gy和4 Gy时，双着丝粒产额和染色体断片产额随LET的变化示于图6。由图6可看出，同一种染色体畸变类型在不同剂量下，产额随LET的变化趋势一致。相同剂量下，双着丝粒产额随LET的增加较明显，而>3 Mbp的染色体断片产额随LET的增加则相对平缓。

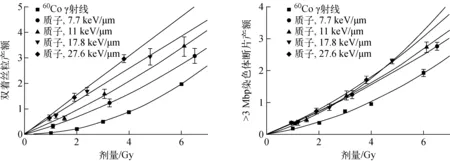
图5 不同类型染色体畸变产额随细胞受照剂量的变化 Fig.5 Variation of chromosome aberration yield with irradiation dose

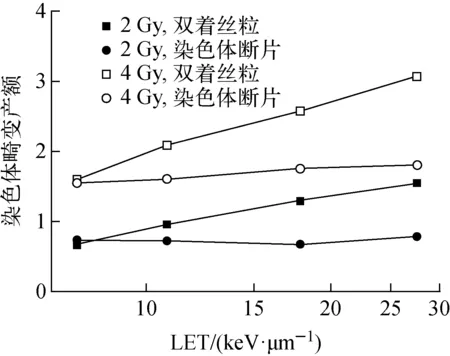
图6 染色体畸变产额随射线LET的变化Fig.6 Variation of chromosome aberration yield with LET of ionizing radiation

3 基于染色体畸变的细胞存活机理模型

基于对NASIC模拟得到的染色体畸变产额数据的分析结果，建立细胞存活机理模型。模型考虑的染色体畸变类型包括双着丝粒、无着丝粒、染色体易位、着丝粒环和>3 Mbp的染色体断片。由于高LET的He离子以及原子序数更大的重离子导致的染色体畸变类型更复杂，所以本文提出的模型适用于光子、质子和低LET的He离子。

假设辐射所致细胞核内双着丝粒产额为Ndic、无着丝粒产额为Nac、染色体易位产额为Ntr、着丝粒环产额为Nring、>3 Mbp的染色体断片产额为Ndel，每种畸变类型对应的致死概率分别为qdic、qac、qtr、qring和qdel。模型推导过程如下：

-lnS=Ndeath

(2)

Ndeath=qdicNdic+qacNac+qtrNtr+

qringNring+qdelNdel

(3)

考虑到无着丝粒和染色体易位与双着丝粒的线性关系，有Nac=k1Ndic、Ntr=k2Ndic。同理，Nring=k3Ndel，将其代入式(3)得：

Ndeath=qdicNdic+k1qacNdic+k2qtrNdic+

qdelNdel+k3qringNdel=(qdic+k1qac+k2qtr)·

Ndic+(qdel+k3qring)Ndel=q1Ndic+q2Ndel

(4)

由式(2)和(4)可得：

S=e-(q1Ndic+q2Ndel)

(5)

其中：S为存活分数；Ndeath为细胞核内平均致死事件个数；q1为与双着丝粒呈线性关系的这一类染色体畸变转化为致死事件的概率；q2为与>3 Mbp的染色体断片呈线性关系的这一类染色体畸变转化为致死事件的概率。

4 细胞存活机理模型验证

4.1 模型参数拟合

本文以V79细胞为例，拟合基于染色体畸变的细胞存活机理模型的参数。采用NASIC模拟的双着丝粒产额和染色体断片产额作为模型输入，细胞存活实验数据作为模型输出，拟合式(4)中的模型参数，得到q1=0.868 5、q2=0.181 6。采用基于染色体畸变的细胞存活模型计算的V79细胞的存活分数与实验数据[24-26]的比较示于图7。由图7可看出，对于X射线和不同LET的质子，模型计算值与实验数据均符合得很好，相关系数R2=0.985 3。模型仅采用2个拟合参数，即可较好地模拟不同LET射线对细胞的致死效应，且能较好地区分不同LET射线在细胞致死效应上的差异。

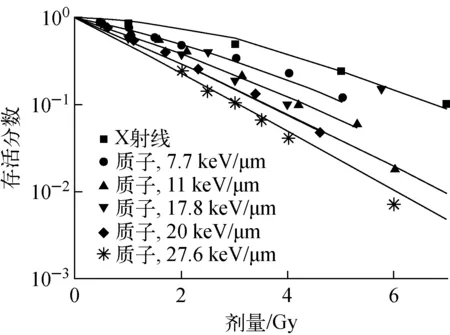
图7 V79细胞存活分数的基于染色体畸变的模型模拟值与实验数据的对比Fig.7 Comparison between modelled data andexperimental data of cellular survival

4.2 模型验证

采用4He离子的细胞存活实验数据对建立的细胞存活机理模型及参数进行验证。模型计算的细胞存活分数与4He离子细胞存活实验数据[27-28]的比较示于图8。模拟值与实验数据的相关系数R2=0.931 1。可见，建立的模型也适用于4He离子，且能较好地区分不同LET射线在细胞致死效应上的差异。

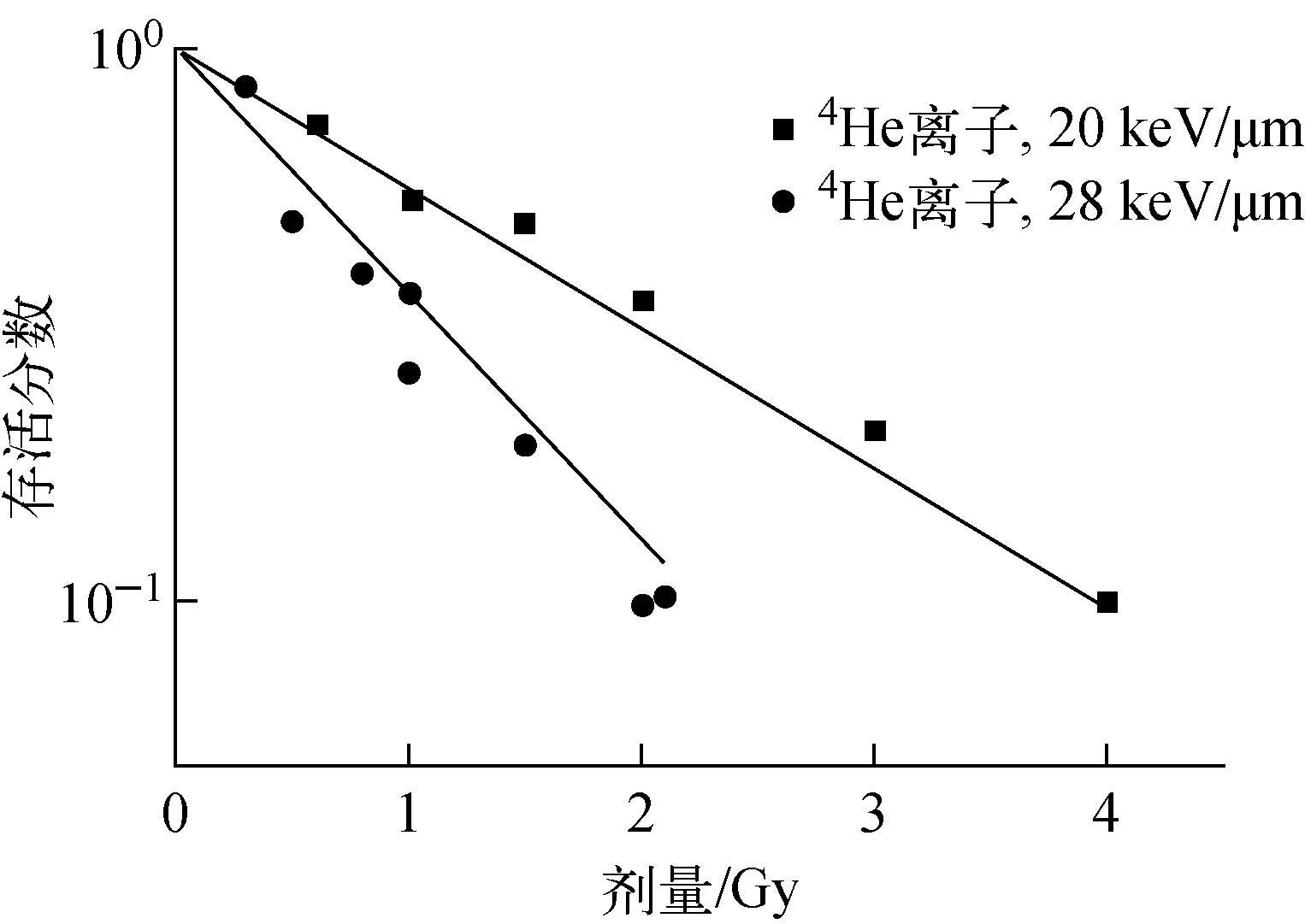
图8 V79细胞基于染色体畸变的细胞存活模型验证结果Fig.8 Validation of proposed cellular survival mechanistic model with experimental data of V79 cell

4.3 与LQ模型的比较

本文建立的基于染色体畸变的细胞存活机理模型，不同剂量、不同品质射线致死效应的差异体现在所致染色体畸变产额的差异上。从图5可知，对于光子和低LET射线，剂量较低时，染色体畸变产额与剂量呈线性平方关系，但由于细胞核内染色体的数目一定，染色体畸变的产额不会随剂量一直呈线性平方增加。图9为NASIC模拟的60Co γ射线所致双着丝粒产额随细胞受照剂量的变化，剂量较低时，双着丝粒产额随剂量呈线性平方增加，随着剂量的增加，双着丝粒产额由线性平方增加变为线性增加。LQ模型中，细胞核内平均致死事件个数随剂量呈线性平方增加，而本文建立的细胞存活机理模型，细胞核内平均致死事件个数随剂量的变化由线性平方增加变为线性增加，从而避免了LQ模型在高剂量下对辐射致死效应的过高估计。

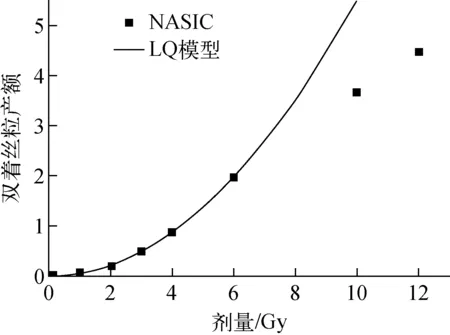
图9 60Co γ射线照射所致双着丝产额随剂量的变化Fig.9 Variation of dicentric yield induced by 60Co γ radiation with dose

CHO细胞和HeLa细胞在高剂量X射线照射下，基于染色体畸变的细胞存活模型与LQ模型估算的细胞存活分数的对比示于图10。可看出，LQ模型在高剂量下会高估辐射的致死效应，与LQ模型相比，文本建立的细胞存活机理模型在高剂量下与实验数据[29-30]符合得更好。

5 结论

本文开发了NASIC程序的DNA损伤修复模块，用于模拟DNA受到辐射损伤后的修复过程，从而得到不同类型射线、不同LET辐射所致细胞核内不同类型染色体畸变的产额。在分析染色体畸变产额变化规律的基础上，建立了基于染色体畸变的细胞存活机理模型。该模型适用于光子、质子和低LET的He离子所致离体细胞致死效应的评估，避免了LQ模型在高剂量下对辐射致死效应的过高估计，而且不同于LQ模型，该模型具有同种细胞的模型及参数适用于不同类型射线、不同LET射线的优点。

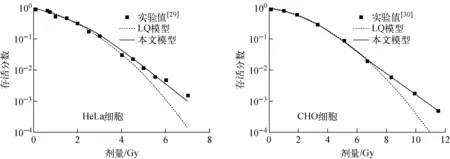
图10 高剂量X射线照射下本文模型与LQ模型估算的细胞存活分数的对比 Fig.10 Comparison of cell survival estimated by model in this paper and LQ model under high dose X-ray irradiation