电子储存环注入过程中补注电荷的三维位置信息提取

周逸媚，冷用斌,*，张 宁，高 波，陈之初

(1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院大学，北京 100049；3.中国科学院 上海高等研究院，上海 201204)

上海同步辐射光源(SSRF)是1台高性能的第3代同步辐射光源，由150 MeV的电子直线加速器、3.5 GeV增强器和3.5 GeV的电子储存环组成，于2009年建成交付用户使用，其储存环的基本参数为能量3.5 GeV，环周长432 m，射频频率499.654 MHz，回旋周期1.44 μs，谐波数720，束流平均流强200～300 mA[1-2]。

为向用户提供更为稳定的同步辐射，上海同步辐射光源自2012年开始采用恒流运行模式(top-up模式)[3]，每5～10 min对储存环进行小电荷补注。对光源用户而言，此注入过程会对实验结果产生扰动，需研究并优化注入过程中注入器与储存环的匹配度，从而将其影响降到最低。

另一方面，储存环中的束流在注入完成后，运行非常稳定，横向振荡振幅通常被压制在μm量级[4]，纵向振荡振幅通常被压制在ps量级[5]。在此状态下，如果不外加激励(扰动)就无法测得最基本的动力学参数(如Beta函数、工作点、阻尼时间等)，难以判断光源是否运行在设计模型下以及是否存在运行风险。而束流注入瞬态过程将迫使储存束流暂时偏离稳定状态，对束流测量而言，是储存环动力学参数原位诊断的最佳时间窗口[6]。如能在定期的注入过程中监测束团三维参数，就可借助对这个非稳态过程的分析获取多个机器动力学参数，从而对注入过程中注入器与储存环的匹配度进行分析，精确评估运行装置的注入系统性能并给出明确的优化指导方向。

对下一代趋于衍射极限的同步辐射光源而言[7-8]，具有超低发射度和超小束流真空室的特点，无论是在轴横向置换注入方式还是在轴纵向累积注入方式[9-11]，对注入过程中的储存束流和补注束流横向和纵向匹配度要求均更高，如能实时精确监测储存束及注入束的三维位置演化过程，对于机器参数的优化调整和注入方案性能的评估将有很大帮助。

对储存环中的高能电子束流而言，其主要作用的是磁场力及尾场作用，与这两者相比，空间电荷效应可忽略不计。注入过程中补注电荷的三维位置信息提取在横向上，由于漏场作用，注入后横向位置表现为明显的betatron衰减振荡，且由于每个束团的漏场不同，导致振荡幅度和初始相位均不同，本文提出一种位置提取方法获取betatron振荡振幅和衰减时间，同时还可监测betatron振幅分布和工作点演化等信息，便于尾场、阻抗以及储存环稳定性和重复性等问题的研究；在纵向上，由于纵向振荡频率较低，可认为每个束团近似为相同的共模振荡，提取的补注电荷的相位表现为同步衰减振荡，为获取同步振荡振幅、同步振荡阻尼时间以及初始到达时间等参数，本文提出比例系数法。

1 基本原理

环形加速器中[12-13]，粒子运动轨迹的切线方向为纵向(z方向)，与纵向垂直的平面为横向，如图1所示，其中水平面内垂直于纵向的方向为水平方向(x方向)，而垂直于水平面的方向为垂直方向(y方向)。注入瞬态过程是补注电荷(图1中红色小球)与储存电荷(图1中蓝色小球)随时间融合的过程，在此过程中补注电荷和储存电荷均会发生横向位置和纵向相位的偏移。由于储存电荷的振荡幅度较小，主要关注补注电荷的三维位置振荡情况，如何从融合后的测量结果中提取所需补注电荷信息是电子储存环中的1个难题。

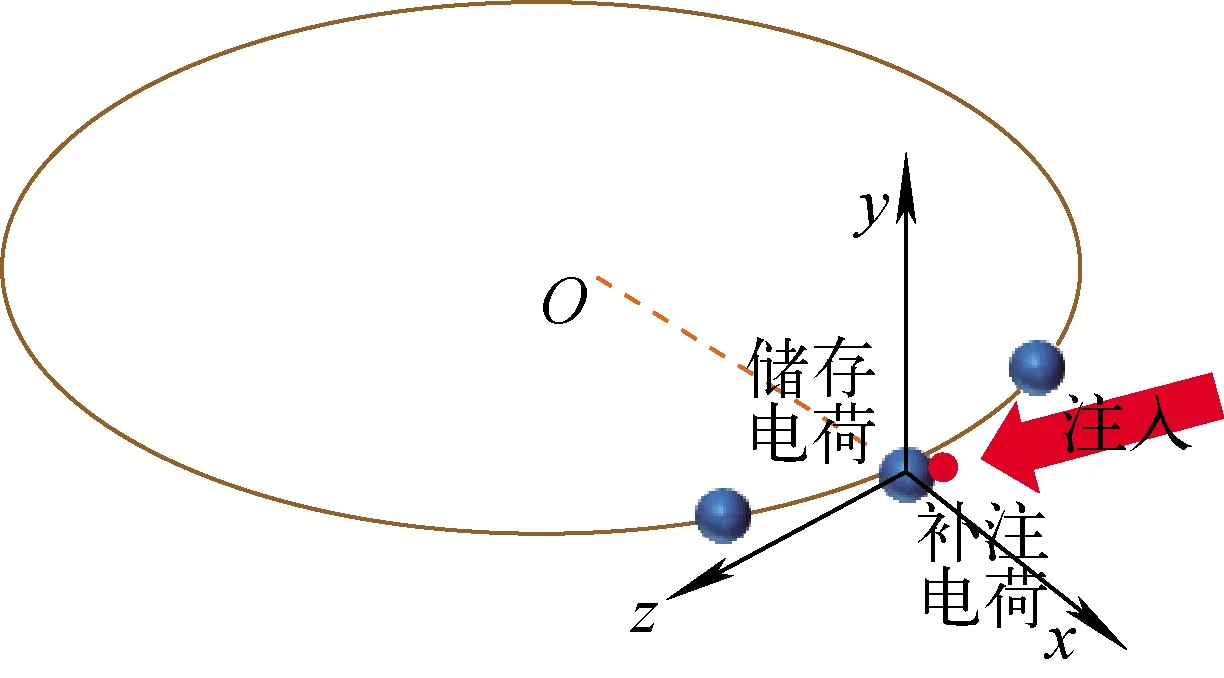
图1 储存环束团注入瞬态过程(自然坐标系)Fig.1 Beam injection transient process in storage ring (natural coordinate system)

1.1 纽扣型束流位置探测器(BPM)信号分析

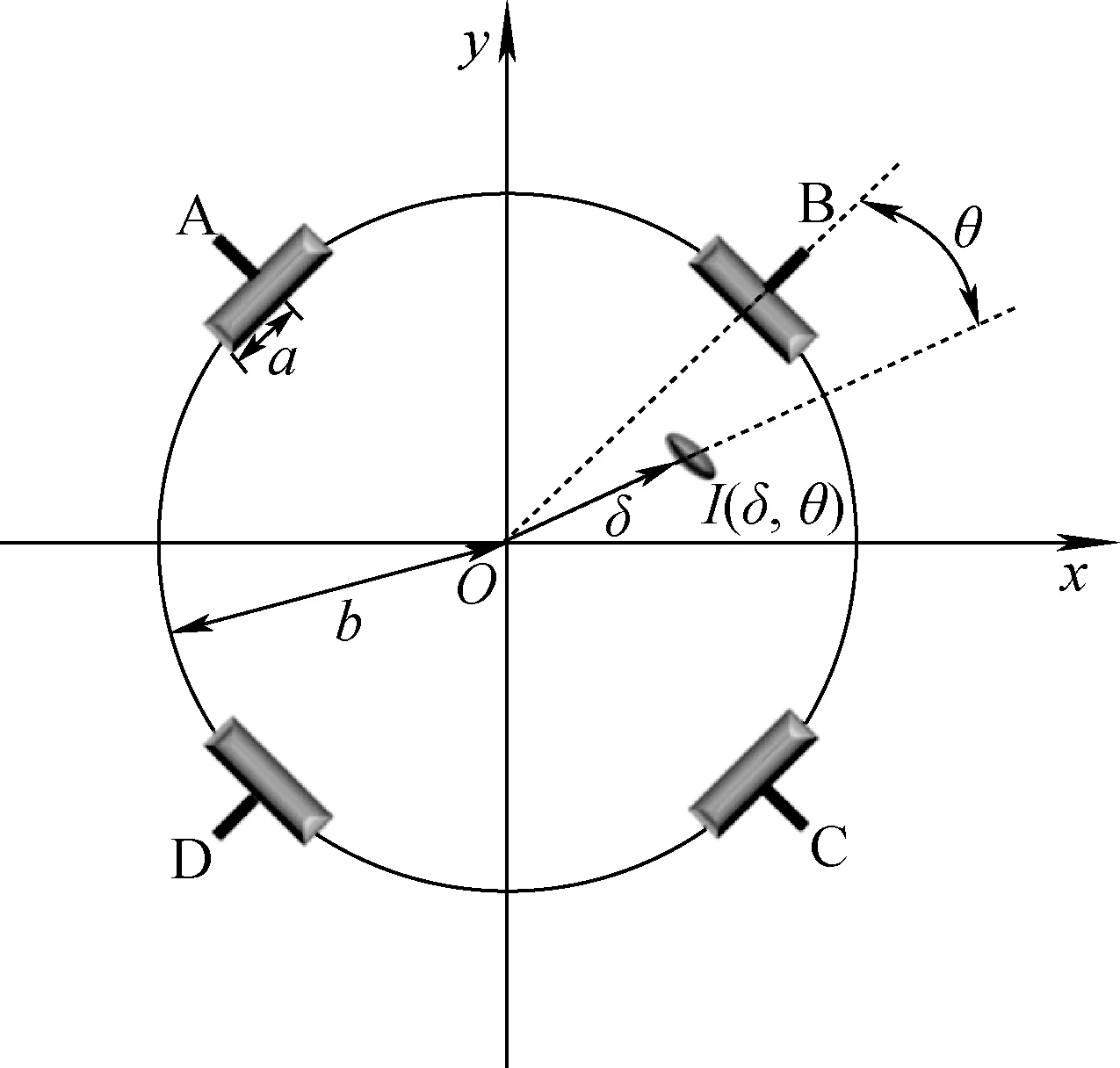
图2 纽扣型BPM截面框图Fig.2 Cross section of button-type BPM

为满足束流诊断系统需要，上海同步辐射光源储存环共安装了140个纽扣型BPM，其中1个用于精确测量逐束团三维位置。当束流经过纽扣电极中心时，每个电极得到的感应电压与纽扣电极表面到束团的距离密切相关。所以当束团穿过纽扣电极的非中心位置时，4个电极上的感应电压各不相同。图2为纽扣型BPM的截面图，当真空室半径为b、探头半径为a时，(δ,θ)处束团的感应电压[14-16]为：

(1)

式中：β为束流运动速度；c为光速；Z为等效传输阻抗，主要由探头阻抗、信号网络阻抗、电子学阻抗共同确定；F(δ,θ)为束团中心的位置偏移信息；t为相位，即时间；流强I(t)满足高斯型分布：

(2)

式中：Q为束团电荷量；t0为束团纵向相位；σ为束团纵向束长。

当探头的几何形状确定后，BPM感应电压信号主要与F(δ,θ)、Q、t0、σ有关，因此，从纽扣电极获得的感应电压信号即可分离出束团的三维位置信息。

1.2 束团横向betatron振荡分析

注入过程中，由于注入器与储存环不匹配，在补注电荷与储存电荷融合的过程中会发生横向位置的振荡，该振荡满足阻尼衰减振荡，通常称为横向betatron振荡[17]：

(3)

方程以轨道路径s为自变量。上式中：x(s)为横向振荡的方程；A和ω为与初始条件相关的积分常数；ψ(s)为横向振荡的相移；β(s)为关于s的周期函数，表征了横向振荡振幅的最大包络，也称为包络函数。

1.3 束团纵向同步振荡分析

纵向相位是束团在每个时刻相对于RF参考信号的相位差。在小幅度振荡时，束团纵向运动满足典型的阻尼衰减振荡[18-19](式(4))，注入过程中补注电荷的相位振荡即满足这种同步振荡。

(4)

其中：z为补注电荷的纵向振荡的方程；zm为补注电荷的纵向初始最大振幅，表征注入器与储存环的能量不匹配情况；φ0为补注电荷的初始到达时间；Ω为同步振荡频率；αs为纵向振荡阻尼系数，它的倒数即为同步振荡阻尼时间。

2 逐束团三维位置诊断系统

2.1 系统结构

逐束团三维位置诊断系统框图如图3所示，为保证系统前端输入信号的同相位采样，纽扣电极拾取信号经同轴电缆传输后，连接移相器PNR P1214D调节，实现相位补偿。之后各电极信号经功分器分成两路，一路用于横向位置测量，一路用于纵向相位测量。位置信息通过直接采集信号峰值点获取(图4中黑色星号)，相位信息通过采集BPM和信号的过零点获取(图4中绿点)，采样点的位置通过两根固定相位差(300 ps)的延迟线保证。信号的采集主要依赖于两块有效位10 bit、带宽1.2 GHz，每通道采样率为1 GS/s的高速数据采集板卡(ADQ14AC-4C)。数据采集使用外时钟模式，时钟信号来源于整个加速器装置的主定时系统，通过调节时钟外接移相器分别实现对BPM信号峰值点和过零点的采样。

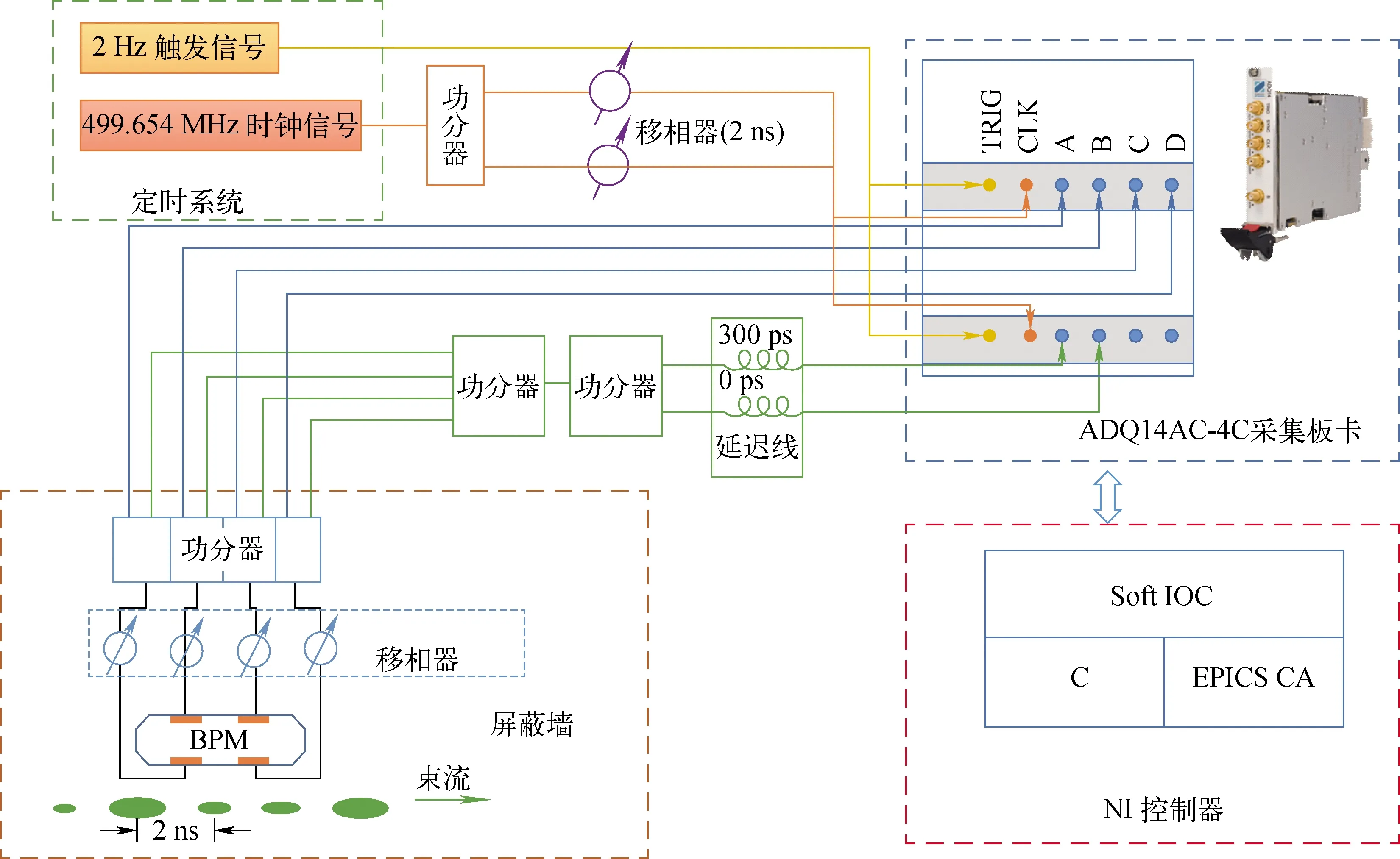
图3 逐束团三维位置诊断系统框图Fig.3 Block diagram of bunch-by-bunch 3D position diagnostic system

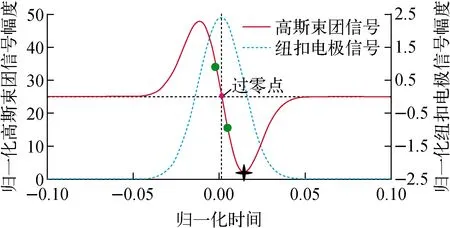
图4 BPM信号采样点示意图Fig.4 Schematic diagram of BPM signal sampling points

实验共采集2 083圈数据，为捕获注入过程中补注电荷的起始注入位置，需设定合适的外触发延迟时间。本次实验注入位置为第56圈，前55圈为储存电荷的数据，是后续三维位置信息提取的重要参考数据。此外，注入过程仅持续2～3 s，如何判断并捕获注入数据是实验的关键。当注入过程开始时，被注入束团的信号幅度有1个跳变，利用这一现象来设置触发阈值，保证捕捉到注入瞬态现象。

2.2 横向位置和纵向相位获取算法

逐束团横向位置主要通过差比和法(Δ/∑)精确获取(式(5))，这种方法去除了电荷量的影响[20]。

(5)

其中，kx、ky为束流位置测量的灵敏度，为探头标定系数。经系统标定后可从归一化电极信号中得到束流水平和垂直的位置信息[21]。

逐束团纵向相位主要采用过零检测法进行测量[5]，即两通道通过相位差为300 ps的延迟线完成BPM和信号过零点附近的两点采样。BPM和信号可去除横向位置和电荷量的影响。

3 注入过程补注电荷的三维位置分析

3.1 注入过程补注电荷的横向位置提取

在注入瞬态过程中，注入器每5～10 min补注5～6个小电荷(pC量级)，补注电荷围绕储存环中已存在的储存电荷(nC量级)逐圈振荡，最后趋于融合。而采集的信号是两者融合后的结果，如何剥离出补注电荷是本文的研究重点。

横向betatron振荡是注入后由漏场引起的残余振荡，由于各束团受到的漏场不同，从而使得横向振荡的振幅和相位存在差异。因此，提出了一种新的数据处理方法——电荷加权平均法提取补注电荷的位置信息(重点关注水平方向位置)。已知注入后的束团由补注电荷和储存电荷组成，假设测得的结果是两者的线性叠加，则根据差比和算法，式(5)可写成：

(6)

其中：Xm为测得的整个注入束团的横向位置；k为补偿因子；Δs、∑s和Δr、∑r分别表示储存电荷和补注电荷的差信号、和信号。

式(6)化简后，补注电荷的横向位置可通过以下公式计算：

(7)

其中，Xs为储存电荷的横向位置，可根据非注入状态下前后储存束团的漏场分布插值获得。

在束团非注入情况下，由于系统带宽远小于束流信号带宽，则在同步采样时，同1个采样点的信号分布与束团长度无关，因此储存束团的信号幅度可认为只与电荷量有关。假设注入束团的储存电荷量与非注入的其他储存束团的电荷分布一致，则可通过注入前55圈的数据来计算储存电荷量Qs，而补注电荷量Qr为注入后与注入前的电荷量之差。因此，式(7)可写成：

(8)

3.2 注入过程补注电荷的纵向相位提取

纵向同步振荡是相对于同步粒子而言的周期性相位变化，是本身固有存在的，并非由束团注入引起，所以可认为在非注入情况储存束团的纵向振荡是一致的，而注入后补注电荷的同步振荡行为由式(4)描述。

在纵向相位处理中，束团之间的串扰问题不可忽视。为提取注入过程中补注电荷的纵向相位振荡，提出了一种基于原始感应电压信号的比例系数法。已知在非注入时，储存束团信号由自身激发的储存电荷和其他储存束团对其造成的串扰信号组成。而注入后的束团，不仅有储存电荷和串扰信号，还有补注的小电荷。因此，提取补注电荷信号Vr只需将测得的注入束团信号Vm减去其储存电荷和串扰信号即可，而所获取的注入前55圈的数据恰好包含了这两部分信息。电荷量差异与串扰差异均是一个定值，可选取任意1个储存束团作为参考束团信号Vs，通过计算与注入束团前55圈的基线之比来获取比例系数K。补注电荷信号可按照下式计算得到：

Vr=Vm-KVs

(9)

为提高测量分辨率，可选取远离注入束团的多个储存束团的平均值计算：

(10)

过零检测法获得的两通道信号均可利用这个比例系数法分别计算出补注电荷的感应电压(Vr1,Vr2)。根据纵向相位的获取方法，通过计算两信号的和差之比，可从查找表中找到补注电荷逐圈对应的纵向相位。

4 束流实验与结果

整个实验在上海同步辐射光源正常供光模式下进行，在束流平均流强为230 mA条件下捕获了注入过程数据，填充模式如图5所示，红色为注入后逐束团电荷量，蓝色为注入前储存束团电荷量，补注束团的位置可从图中直接观测到。图5中可明显看到补注电荷注在编号为605～611的束团上，实验以最大注入电荷量的606号束团为例，补注电荷量为95 pC，注入前该束团储存电荷量为0.61 nC。实验结果通过差比和法和纵向相位查表法获取逐束团的横向位置和纵向相位，并根据电荷加权平均法和比例系数法分别提取补注电荷的位置和相位振荡信息。

图5 注入前、后填充模式Fig.5 Filling pattern before and after injection

根据电荷加权平均法，提取的补注电荷的横向位置结果如图6所示，补注电荷横向位置的逐圈振荡初始最大振幅约为±5 mm，表明储存环与注入器的横向失配情况。

图6 补注电荷横向位置逐圈振荡Fig.6 Extraction of refilled bunch transverse position oscillation

根据比例系数法，提取的补注电荷的纵向相位结果如图7所示。通过式(4)的纵向相位振荡模型拟合，可见测量结果与模型相互吻合，从中可拟合出初始最大振幅为181.6 ps，同步振荡频率为0.007，初始到达时间为0.759 rad(～241.7 ps)以及同步振荡阻尼时间3.26 ms (2 268圈)。通常情况下，同步振荡阻尼时间的测量需特殊的束流运行状态和机器研究时间。然而，在此实验中，可通过在正常供光模式下捕获注入过程，然后提取补注电荷的方式，直接拟合出结果，为束流测量工作者提供便利的研究工具。

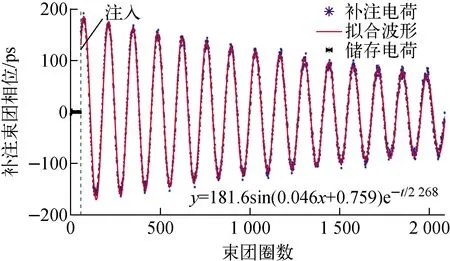
图7 补注电荷纵向相位逐圈振荡Fig.7 Extraction of refilled bunch longitudinal phase oscillation

在纵向运动中，补注电荷相位振荡的最大振幅和初始到达时间表征了储存环与注入器的能量失配情况，此次提取的结果可用于储存环动力学的研究，也是评估储存环与注入器匹配程度的重要工具，同时也为下一代同步辐射光源的注入方法和注入性能的评估提供了参考工具。

5 结论

上海同步辐射光源开发了1套逐束团三维位置同步诊断系统，可从BPM纽扣电极信号中直接提取出逐束团三维位置信息，分别通过差比和算法和过零检测法计算出横向位置和纵向相位。

本文提出了两种新的数据处理方法——电荷加权平均法和比例系数法，可通过分析注入过程中的逐束团位置数据和相位数据，提取出补注电荷在注入后的横向betatron阻尼振荡曲线以及纵向同步阻尼振荡曲线。在不需提供特别的机器研究时间的情况下，实现补注电荷的betatron振荡振幅、同步振荡振幅、初始到达时间和同步振荡阻尼时间等动态参数的原位测量，为加速器物理学提供一套强有力的机器研究工具，有助于分析注入器与储存环的匹配程度，并对机器运行性能的优化提供更为精确的指导意见。