基于低阶图像块和迭代的射线检测图像噪声水平估计

党长营，李建素，曾志强，杜文华

(中北大学 机械工程学院，山西 太原 030051)

0 引 言

由于射线检测过程的特殊性及其固有成像特点，射线检测数字图像往往含有大量的噪声.特别对于传统射线检测底片来说，它本身就含有一定量的噪声，而且在对其进行数字化的过程中也会不同程度地引入噪声，因此，数字化后的射线检测图像一般都叠加了多种不同种类的噪声.其中，主要的噪声有射线源产生的噪声、射线散射噪声、底片颗粒度噪声、数字化仪的电子噪声、数字化系统产生的量化噪声、其他干扰噪声等[1-2].这些噪声不仅对射线图像质量、预处理、缺陷分割、特征提取、缺陷识别等有不利影响，而且会间接影响缺陷识别系统的精度和效率.

鉴于数字化后射线检测图像上叠加了多种噪声，射线检测图像降噪已经成为不可缺少的技术环节，用以提高射线检测图像的质量、为后续图像处理提供较好的基础图像.对于图像降噪来说，图像噪声水平又是一个至关重要的参数，且噪声水平评估的性能直接影响降噪算法的性能.截止目前，精确地估计出多种多样的图像噪声水平仍然是一个挑战[3].尤其是射线检测图像具有噪声大、对比度低、图像模糊、灰度区间窄、背景起伏大等显著特征，容易导致噪声水平估计的不准确，对噪声水平估计方法的性能又提出更大的挑战和要求.

一般而言，图像噪声可以分为两大类：周期性噪声和随机性噪声.周期性噪声往往可以通过线性操作滤除；但随机性噪声的有效滤除仍然是学者们研究的热点之一[4].随机性噪声一般可建模为可加性或乘性于图像信号的随机信号.在数字图像中，随机噪声的主要成分是电子噪声，通常被建模为加性噪声.零均值正态分布的高斯白噪声被认为是最典型的加性噪声模型，并可以在图像采集或传输过程中独立地添加到像素强度中.换言之，可以将图像噪声水平估计的问题转化为图像中高斯白噪声标准差(σn)的求取问题.

常用的噪声估计方法主要可分为基于变换的方法、基于滤波的方法、基于统计的方法、基于图像块的方法等[5-6].

在基于变换的方法中，通常先将图像从空间域变换其他域，如奇异值分解(SVD)域、小波变换(WT)域、离散小波变换(DWT)域、离散余弦变换(DCT)域等，然后再进行图像噪声估计[4,7].其中，基于SVD变换的方法利用奇异值序列来估计图像噪声水平，以减轻图像基础结构对噪声估计过程的影响[8].该类方法将奇异值分为两部分：噪声影响部分和无噪声图像影响部分，并认为无噪声图像影响部分是固定的.但是，无噪声图像影响部分可能随着噪声方差的变化而变化，特别是对于低噪声水平或高频图像(强结构图像).因此，当噪声水平低或图像包含大量的特征时，基于SVD变换的估计方法易于对噪声水平估计过高.基于WT变换的方法利用小波变换分离出第一对角带系数中的噪声信息，然后根据这些系数的绝对值来估计图像噪声水平[7].但是，该类方法是基于最细分解水平(HH1子带)的小波系数只对应噪声分量的假设，对高频图像的噪声估计时也易于过高估计.基于DWT和DCT变换的方法通过匹配DWT域或DCT域系数矩来估计图像噪声水平.然而，DWT和DCT一般很难将图像信号从噪声图像中完全分离出来.

在基于滤波的方法中，首先利用低通滤波对图像进行噪声抑制，然后通过分析图像和滤波图像的差异来估计图像噪声水平[7].该类方法面临的主要挑战是图像和滤波图像之间的区别被假设为纯噪声信号.但这种假设并不普遍成立，因为低通滤波图像不一定是理想的无噪声图像，尤其是当图像有复杂的、丰富的结构或精致的纹理时.因此，大部分基于滤波的估计方法对于高噪声水平和纹理较少的图像具有较好的效果，但对于高频图像容易过估计噪声，且它们的计算复杂度也比较高.

在基于统计的方法中，通过分析图像在空间域或变换域(如DWT和DCT域)数据的统计特性，并采用合适的统计模型来估计图像噪声水平[7,9].比如，基于DWT统计的方法假定图像小波分量为拉普拉斯分布(Laplacian distribution)模型，通过匹配模型数据的真实峰度(Kurtosis)值和估计峰度值来估计高斯噪声方差.类似地，基于DCT统计的方法也为无噪声图像DCT块对应频率分量的交流(AC)系数假定了相同的峰度值.然而，它实际上并没有利用广义高斯分布(GGD).此外，在匹配噪声频率分量对应系数的峰度值时，它最小化了总绝对误差值.可以看出，基于统计的方法的性能对所采用模型的准确性非常敏感.在这种情况下，存在的问题是容易过估计低噪声图像的噪声水平.

在基于图像块的方法中，首先将图像细化为许多图像块，然后从一系列特别选出的同质(Homogeneous)图像块中计算出噪声方差[5,7].该类方法最主要的假设是同质图像块由绝对平滑的图像块和噪声构成.实际上，图像同质性是一个相对概念，并且一个相对同质的图像块也可能包含一些其它图像信息.此外，如何用适合图像的模型参数来识别同质图像块是该类方法必须要面对的瓶颈问题.不同该类方法的最大不同之处就是如何选择同质图像块的差异.一般而言，该类方法运算简单，但估计性能依赖于输入图像和噪声水平[9].也就是说，它们可能过估计低噪声水平或欠估计高噪声水平.为解决此问题，学者们又将不同的方法如亚像素[4]、DCT、边缘检测[6]、主成分分析(PCA)、滤波[9]、蚁群优化[10]等应用于低阶图像块(Low-rank image patch)和图像纹理，以选择最佳同质图像块.

目前，针对数字化后射线检测图像上叠加的多种类型噪声，射线检测图像的预处理主要聚焦于图像降噪和图像增强，但针对射线检测图像噪声水平的有效估计仍然是一个较大的挑战，相关的研究成果也鲜有报道.因此，基于以上分析和射线检测图像的特点，本文提出一种基于低阶图像块和迭代的射线检测图像噪声水平评估方法(NELRI).在本文中，首先分析了射线检测图像的噪声成分，然后介绍了所提评估方法的基本原理，最后进行了相关实验验证和分析.

1 射线检测图像的噪声成分

为了有效地对射线检测图像进行噪声水平评估，需要对射线检测图像的噪声成分进行分析和研究.

传统射线检测底片经数字化后便得到数字图像(即射线检测图像)，但射线检测底片上一般含有射线源产生的噪声、射线散射噪声、底片颗粒度噪声等，而且底片在数字化过程中也可能引入数字化仪的电子噪声、数字化系统产生的量化噪声或其它干扰噪声[1]，因此射线检测图像叠加了多种类和成分的噪声(即混合噪声).

本文的研究对象就是传统射线检测底片数字化后得到的射线检测图像，数字化仪与计算机之间采用Camerlink方式传输，传输距离不超过1 m，因此，图像传输信道影响的乘性噪声可以忽略不计，本文主要关注射线检测图像中的加性噪声.这类噪声大部分是数字化仪光电转换过程中产生的，主要包括暗电流噪声、散粒噪声、量化噪声，除此之外，传统射线底片也包含一定量的胶片颗粒度噪声.

1)胶片颗粒度噪声

胶片颗粒度噪声是由于卤化银颗粒分布的随机性、射线光子吸收的随机性而产生的.研究表明[1,11]，胶片颗粒噪声的分布特性可以用均值为0的高斯白噪声来有效描述，噪声标准方差与局部颗粒平均密度的立方根成正比.

2)暗电流噪声

暗电流噪声的来源有两种：一种是耗尽层热激发产生的热噪声，这个随机过程，可以用高斯分布来描述；另外一种是CCD阵列中局部晶格缺陷或夹杂造成的暗电流尖峰，可用椒盐噪声来描述[12].经实验分析，本文采用的射线检测图像均没有暗电流尖峰，即暗电流噪声仅包含了热噪声[1].由于热噪声服从高斯分布，故暗电流噪声可以采用高斯噪声来描述.

3)散粒噪声

CCD将光子转换为电荷的过程是一个独立、均匀、连续发生的随机过程，由于光具有粒子特性，即使入射光强度均匀，单位时间内CCD感光单元接受到的光子数目也不一定完全相同，而是在一个均匀值上做微小的波动，这个微小的波动便形成散粒噪声.在大量光子存在的情况下，散粒噪声呈高斯分布[1,12].

根据以上分析，射线检测图像的主要噪声成分为胶片颗粒度噪声、暗电流噪声和散粒噪声，且均可用高斯分布来描述[1]，因此射线图像的混合噪声分布模型可表示为

ε(x,y)=εf(x,y)+εd(x,y)+εs(x,y),

(1)

式中：ε(x,y)为混合噪声；εf(x,y)为胶片颗粒度噪声；εd(x,y)为暗电流噪声；εs(x,y)为散粒噪声.

2 NELRI的算法原理

基于低阶图像块和迭代的射线检测图像噪声水平估计方法(NELRI)的算法原理如图 1 所示，主要由初始噪声估计、低阶图像块选择、纹理强度阈值计算、迭代噪声水平估计等四部分构成.

图 1 NELRI的算法原理示意

2.1 初始噪声的估计

初始射线检测图像噪声水平估计的思想是将噪声图像进行分块，然后通过噪声图像块(Noisy patch)的协方差矩阵来估计图像噪声水平.

根据Liu等人研究[3]可知，含噪声图像块yi和无噪声图像块zi协方差矩阵的最小特征值存在以下关系：

λmin(Σy)=λmin(Σz)+σn,

(2)

式中：λmin(Σ)为协方差矩阵Σ的最小特征值；Σy为含噪声图像块yi的协方差矩阵；Σz为无噪声图像块zi的协方差矩阵；σn为噪声标准差.

根据式(2)，如果能够分解噪声图像块协方差矩阵的最小特征值，就可以容易地估计射线检测图像的噪声水平.然而，该分解是一个病态问题，因为无噪声图像块的协方差矩阵的最小特征值(即λmin(Σz))是未知的.

由于图像信息的冗余性，图像数据只跨越(Span)低维子空间RN×N(N为图像块的尺寸).如果无噪声图像块数据({zi}∈RN×N)跨越维数小于N×N的子空间，则将这些子空间称为低阶图像块(Low-rank patches)，因此最小特征值λmin(Σz)能够被假定为0.由于高斯噪声在所有方向上的能量和所有特征值是相同的，所以能够通过低阶图像块协方差矩阵(Σy)的特征向量估计射线检测图像噪声水平，即有

(3)

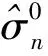
2.2 低阶图像块的选择

由于图像的冗余性假设不一定总是成立，尤其是对于具有精细细节的射线检测图像，容易导致噪声水平出现过估计或欠估计问题.为了克服这一问题，比较可行的方法是从噪声图像中选择没有高频成分的低阶图像块集合.

本研究采用的是通过纹理强度指数来选择低阶图像块[3]，该指数是基于局部图像梯度矩阵和它们的统计特性获得的.

梯度协方差矩阵能够有效地测量图像的结构信息[13]，对于图像块yi，它的梯度矩阵Gyi(N2×2)可表示为

Gyi=[DhyiDvyi],

(4)

式中：Dh为水平方向求导矩阵；Dv为垂直方向求导矩阵.

Dh和Dv是Toeplitz矩阵，可通过梯度滤波得到.此外，图像块yi的梯度协方差矩阵Cyi可表示为

(5)

式中：T为矩阵转置符号.

大量的图像块信息可以通过梯度矩阵Gyi或梯度协方差Cyi来反映，主方向和它的能量可以通过测量Cyi的特征向量和特征值得到，即有

(6)

式中：V为Cyi的特征向量；s1和s2为Cyi的特征向量.

根据式(6)，可以推断出协方差矩阵Cyi的迹(Trace，所有特征值之和)能够反映图像块的纹理强度，迹越大说明图像的纹理越丰富.因此，纹理强度被定义为

ξi=tr(Cyi),

(7)

式中：ξi为纹理强度；tr(·)为求迹运算符.

2.3 纹理强度阈值的计算

通过对纹理强度进行阈值化，可以很容易地将不存在高频成分的低阶图像块从没有噪声的图像中区分出来.但是，梯度矩阵对噪声比较敏感，纹理强度很容易受到噪声的影响，因此需充分考虑噪声对纹理强度计算的影响.

一种极端情况是低阶图像块被认为是平的(Flat)，如果一个完全不含噪声的平图像块为zf，那么它的梯度矩阵Gzf可以表示为

Gzf=[DhzfDvzf]=[0 0].

(8)

一个存在高斯噪声的图像块yf可以表示为

yf=zf+n,

(9)

式中：n为高斯噪声块，其标准差为σn.

根据式(8)和(9)，可以计算含噪声图像块的梯度矩阵满足

Gyf=[Dh(zf+n)Dv(zf+n)]=

[DhnDvn].

(10)

进一步，含噪声图像块yf的纹理强度ξ(n)可表示为

(11)

为了分析纹理强度的统计特性，可以通过伽马分布(Gamma distribution)来近似估计ξ(n)的分布[3]，则有

(12)

式中：Gamma(α,β)为Gamma分布；α,β分别为形状参数和尺度参数.

为了选择弱的纹理图像块，设定了一个空假设(Null hypothesis)：给出的图像块是含有高斯噪声的，且平的图像块.如果图像块满足该假设，则被选择为弱低阶图像块，并且包含ξ(n)的置信区间被定义为

P(0<ξ(n)<τ)=δ,

(13)

式中：P为求概率符号；τ为纹理强度阈值；δ为置信度.

根据式(13)，如果图像块的纹理强度低于阈值τ，则空假设被接受，并且该图像块被视为弱纹理块.同时，阈值τ可以被表示为给定的有效置信水平δ和噪声水平σn的函数，即有

(14)

式中：F-1(δ,α,β)为逆伽马累积分布函数；N2为图像块的像素数.

2.4 迭代噪声水平的估计

步骤3，利用纹理强度阈值τk+1，从噪声图像中选择弱纹理图像块集合Wk+1；

图 2 迭代噪声水平估计流程图

3 实验结果与分析

为了验证本文NELRI法的精度和效率，将它与常用的噪声估计方法，如Daniel Zoran 的尺度不变噪声估计方法(Scale Invariance Estimation, SCIE)[14]和Jeny Rajan的基于局部方差和偏态的噪声估计(Local Variance and Skewness Estimation, LVSE)[15]，进行对比实验.

实验中，所采用的射线检测底片均来自某大型燃气轮机制造企业的实际射线探伤过程.对应的射线检测数字化图像均是经前课题组为该企业研制的JD-RTD200 射线底片数字化仪扫描得到，该数字化仪达到了欧洲EN14096 标准中数字化要求最高的DS 级.此外，实验条件如下：射线检测的对象是大型燃气轮机中主机关键部件的焊缝，实验中的缺陷也来自上述焊缝的实际检测过程；PC计算机的配置为 Pentium(R)Dual-Core CPU E6500, 2.93 GHz,3G RAM, WIN7；所有算法都编程和运行在MATLAB R2012b(Version 8.0 32-bit win32)上.

采用多幅射线检测图像进行了实验，并且对实验图像添加了均值为0，噪声标准差(SD)从0～40变化的高斯噪声，以验证在不同图像和不同噪声水平下各噪声估计方法的性能.由于多幅实验图像噪声评估的相似性，将以一幅含气孔缺陷的射线图像为例进行说明，原射线检测图像和添加不同噪声水平的噪声图像如图 3 所示，它们的大小均为512×512像素.

图 3 添加不同噪声水平的射线检测图像

在不同噪声水平下，不同方法估计的噪声标准差如图 4 所示.从图中可以明显看出：本文NELRI法的噪声标准差值更接近真实值；SCIE法和LVSE法的噪声标准差值偏离真实值较大，存在较大的欠估计和过估计问题，且 SCIE 法在噪声标准差大于30时存在估计失效的问题.

图 4 不同方法估计的噪声标准差

为了定量地描述各方法的估计精度，对多次估计的偏差进行统计和分析，获得不同方法的估计偏差均值和方差如表 1 所示，其中，估计偏差均值的正负号分别表示过估计和欠估计.可以看出：NELRI法的估计偏差均值和方差均小于SCIE法和LVSE法的，具体地，本文方法的估计偏差均值比SCIE法和LVSE法分别低了75.55% 和84.02%；NELRI法的估计偏差方差比SCIE法 LVSE法分别低77.78% 和 96.28%.因此，说明NELRI法在对射线检测图像噪声水平估计时有较高估计精度.

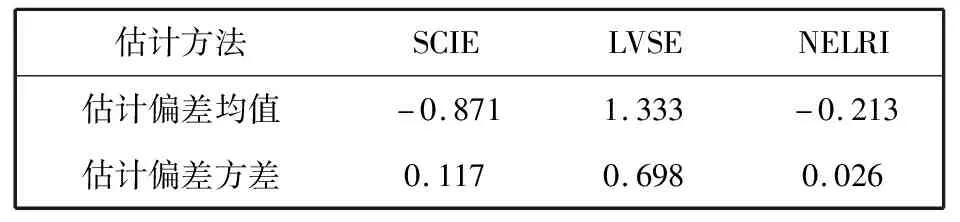
表 1 不同方法的估计偏差均值和方差

此外，为了比较上述不同方法的估计效率，分别对不同方法的多次估计耗时进行计算，获得不同方法的平均耗时如表 2 所示.从表中可以看出，NELRI法的耗时明显低于SCIE法和LVSE法的，且分别低了56.48%和46.07%，说明NELRI法在对射线检测图像估计时有较高的估计效率.

表 2 不同方法的估计运算耗时

4 结 论

针对射线检测图像噪声水平估计过分依赖混合噪声模型和估计易失效的问题，提出一种基于低阶图像块和迭代的射线检测图像噪声水平估计的方法(NELRI).该方法利用低阶图像块、纹理强度阈值、迭代等思想，较好地解决了射线检测图像噪声水平估计容易失效的难题.最重要的是，该方法可以有效地估计噪声水平，而不敏感于射线检测图像的大噪声、对比度低、图像模糊、灰度区间窄等特征.

实验结果表明，NELRI法在对射线检测图像进行噪声估计时具有较好的估计精度、效率和可靠性.最重要的是，它在射线检测图像和图像降噪及后续图像研究之间建立了良好的桥梁关系，即获得准确的、至关重要的射线图像噪声水平参数.此外，所提估计方法同样适用于CR和DR系统等产生的射线图像，这是因为它们的混合噪声成分虽不存在胶片颗粒度噪声，但暗电流噪声和散粒噪声仍是主要噪声成分.