基于GGA+Ud+Up方法的不同形貌TiO2电子结构性质研究

王松林，任 君，李永祥

(中北大学 化学工程与技术学院，山西 太原 030051)

0 引 言

半导体光催化降解环境污染物已引起人们的极大关注.二氧化钛(TiO2)作为一种光催化全明星级别的半导体材料，具有成本低、光吸收率高、在宽pH值和电压范围内具有良好的化学和光学反应稳定性等优点，在光催化领域具有广阔的应用[1-5].众所周知，TiO2本征禁带宽度(金红石为3.0 eV，锐钛矿为3.2 eV)的主要缺点限制了其在波长小于380 nm的紫外光区的光化学吸收，从而阻碍了其在可见光区的应用.另外，半导体的另一个重要竞争过程是电子-空穴复合，其倾向于阻止载流子向表面转移.因此，为了更好地进行光催化反应，需要有效地延长电子-空穴复合所需的寿命.在大量的实验和理论研究中，人们往往通过在TiO2的晶相中掺杂金属或非金属降低TiO2带隙，以提高TiO2的光吸收和电荷输运效率[6-14].然而，由于理论方法的局限性，很难找到一种合适的方法使得计算带隙值与实验结果吻合，如标准DFT的一个主要缺点是难以用局部或半局部近似(局部密度近似(LDA))和广义梯度近似(GGA))正确地描述过渡金属和镧系元素或锕系元素中的局域d或f电子，这是由于LDA或GGA函数固有的自相互作用误差，导致了对部分占据态的非定域化，并且常常严重低估了TiO2的带隙.为了平衡电子的离域和局域化来克服这些限制，进而得到正确的掺杂和氧缺陷行为，通常采用在位库仑-哈伯德U修正(the on-site Coulomb HubbardUcorrection)和杂化泛函方法来处理电子的自相互作用[15-20].最近一种比较流行的杂化泛函方法HSE(Heyd-Scuseri-Ernzerhof screened hybrid functional)被广泛应用，它是将部分Hartree-Fock(HF)交换函数植入到短程交换相关泛函，并成功地应用于强相关过渡金属氧化物体系.但是，HSE方法还需要选择一个与材料相关的屏蔽HF交换泛函，这意味着需要优化选择一个唯一参数进入HSE杂化泛函.此外，在处理原子数多的大模型体系，杂化泛函方法通常比标准DFT和DFT+U法需要更多的计算机，因而不具有经济性.相比较而言，DFT+U方法具有计算效率高、计算成本低并能得到与实验值吻合的计算结果等优点，更适合于大模型体系的计算和模拟.尽管如此，在有关金属氧化物及其性质的众多研究中，没有一个统一的U值选择标准，这就需要在实际计算过程中进行半经验式的选择.大量的文献结果表明，半经验U值通常是能准确描述各种材料的电子性质的.对于DFT+U，有两种计算方法可选即LDA+U和GGA+U，以前的计算主要将U参数作用于过渡金属d或者f轨道上，而不考虑氧的p轨道，如对于四种不同晶型的TiO2(如图1)，其带隙强烈依赖于U值的选择，并且在低的U值范围内与实验值相比仍然被低估.对于过渡金属氧化物体系，很少有研究者同时考虑在位库仑修正对氧的p电子和过渡金属d电子的协同效应.因此，本文应用密度泛函理论GGA+U方法，选取不同U值作用于Ti 3d和O 2p态，进而考察不同U值对四种不同晶型TiO2带隙结构的影响.

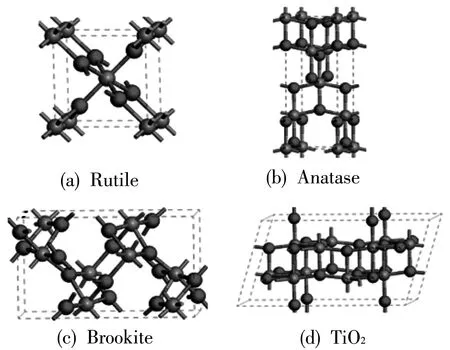
图 1 四种晶型TiO2的结构图

1 计算模型和方法

采用VASP程序包中的GGA+U方法、投影缀加波赝势(Projector Augmented Wave, PAW)和半局域PBE函数，Ti(3p64s23d2)和O(2s22p4)的外层电子被视为价电子，选取截断能为450 eV.采用共轭梯度法进行优化，直到原子力小于0.2 eV/nm，能量收敛阈值为10-5eV.尽管体系没有磁性，仍然选择自选极化方法用于所有计算.第一布里渊区积分采用Monkhorst-Pack网格进行K点采样[21-26].使用有效Ueff(U-J)，其中J为交换参数，因体系没有磁性，设置J=0.对过渡金属氧化物体系的一些早期理论研究讨论过在位库仑修正对氧p轨道电子及其与过渡金属d轨道相互作用的影响.当仅对d轨道实施自相互作用矫正时，氧p轨道不会从LDA或者GGA获得位置偏移，并且所占据的d带远低于氧价带.为了改善这种情况，对包括氧p轨道在内的所有价态进行自相互作用修正.由此可以正确地描述被占据轨道和未被占据轨道之间的能级分裂.本研究中，讨论了U参数作用于氧p轨道和Ti的3d轨道对四种晶型TiO2(图 1)能带结构的影响，并且表明如果同时使用Ud和Up，GGA+U方法可以改善带隙和带边位置.本文将这种方法称为GGA+Ud+Up.为了确定最佳Ud和Up参数，本文系统地考察了Ud和Up，并讨论了它们对能带结构的影响.

2 结果与讨论

首先，只选择不同U值作用于Ti 3d轨道，研究不同U值的四种晶型金红石(Rutile)、锐钛矿(Anatase)、板钛矿(Brookite)和TiO2(B)体相结构的带隙.实验发现不同晶型的带隙值一般在3.0～3.4 eV之间(Rutile[27-29]: 3.0 eV, Anatase[30]: 3.2 eV, Brookite[31]: 3.1～3.4 eV和TiO2(B)[32]: 3.22 eV).对于GGA+U如何确定最优Ud值，到目前为止还没有普遍的共识.在大多数过渡金属氧化物的GGA+U理论计算中，Ud值都是以经验的方式确定的，但也执行了基于U参数的理论确定方法.图 2 数据是只考虑Ud时计算得到的带隙与U值之间的关系，可以看出：四种不同晶型TiO2的带隙值很大程度上取决于U值的选择，随着U值的不断增多而增大，在低U值区无法得到与实验结果相吻合的带隙值.当Ueff值为12 eV时，Rutile的带隙值达到3.0 eV，而Ueff值为9 eV时, Aanatase和Brookite的带隙值与实验值非常接近.不同的是TiO2(B)，Ueff=8 eV时得到与实验数据一致的结果.这意味着GGA+U结果与杂化泛函(HSE06)和多体微扰理论(MBPT-GW)[33-34]方法的数据范围非常吻合.

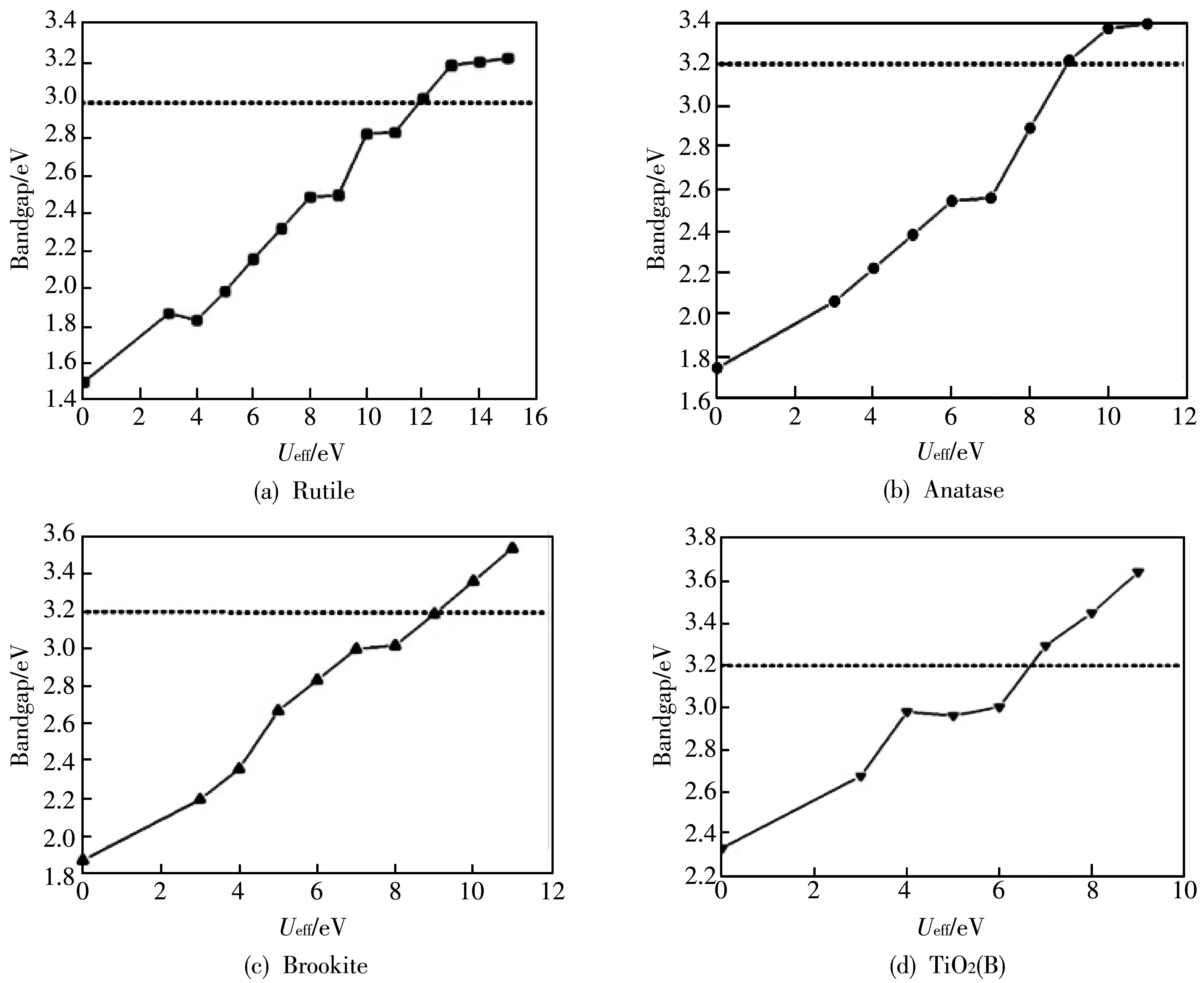
图 2 四种晶型TiO2的带隙值与不同Ueff值的关系

尽管可以通过不断地增大Ud值来满足实验获得的带隙值，但是这似乎也不具有实际的物理意义.除非选择较大的Ud值，否则带隙值仍然被低估.因而GGA+Ud方法也许不太适合计算不同形貌TiO2化合物的电子结构.因此，为了能较合理地描述四种晶型化合物的能带结构，将在位库仑修正对氧2p轨道的作用作为另一重要参数进行了计算.表1总结了四种不同晶型TiO2用GGA+Ud+Up方法和GGA+U方法计算得到的带隙值.对于Rutile，Anatase和Brookite，设定Ud=8 eV，Up分别为 6 eV，4 eV，4 eV, 计算得到的带隙值与实验值非常接近.对于TiO2(B)，设定Ud值为4 eV，Up=4 eV，计算得到的带隙值为3.21 eV，与实验值3.22 eV 非常吻合.在以前的研究中，Calzado等[35]选择Ud值为5.5 eV来描述TiO2的缺陷态，但是仍然低估了带隙值，另外，当Deskins等[36]用Ud=10 eV 计算Rutile-TiO2的带隙，计算结果接近实验值.而在本工作中，我们不仅充分考虑了Ti原子的d-d 库伦相互作用，同时引入O 2p电子对d电子的库伦作用，进而得到能满足实验结果的Ud+Up值.

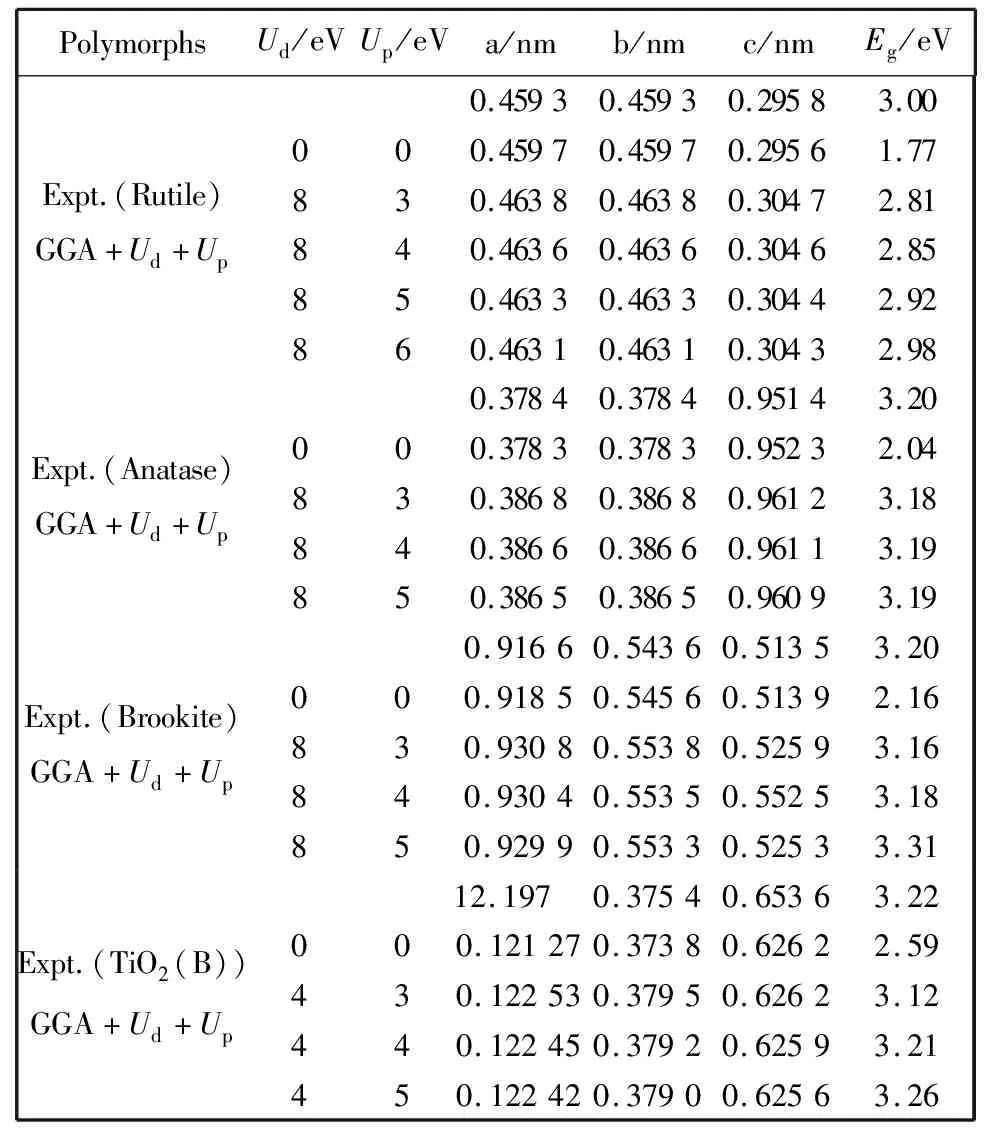
表 1 晶胞参数和带隙的GGA+Ud+Up计算值与实验值比较

为了更好地理解Ud和Up协同效应，本文用GGA+Ud+Up计算了不同表貌TiO2化合物的态密度、能带结构和电子-空穴的有效质量，如图 3 所示.结果表明，四种晶型TiO2的价带顶(VBM)保持不变，导带底(CBM)上移，从而导致带隙增大，获得与实验值相符的结果.光催化活性不仅仅受到带隙结构的影响，还受光生电子和空穴迁移率的影响.载流子移动越快，光致电子-空穴的复合越少，成对的光诱导载流子的迁移率可以描述为

(1)

式中：ν是载流子的迁移率；q是载流子电荷；τ是散射时间；m*是载流子的有效质量.可以看出，迁移率与有效质量的倒数成正比，即光生载流子的有效质量越轻，其传输速度越高.

有效质量为

(2)

式中：E为波矢量k函数的带边能量；h为约化普朗克常数.

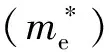
图 3 GGA+Ud+Up方法计算得到的四种晶型TiO2能带结构和态密度图

3 结 论

本文应用密度泛函理论GGA+U方法，计算了四种不同晶型TiO2的电子结构性质.由于传统密度泛函理论LDA和GGA方法具有致命的自相互作用误差过渡，从而严重低估了过渡金属氧化物的带隙值.以前的计算主要将U参数作用于过渡金属d或者f轨道上，而不考虑氧的p轨道，如对于四种不同晶型的TiO2，其带隙值强烈依赖于U值的选择，并且在低的U值范围内与实验值相比仍然被低估.对于过渡金属氧化物体系，很少有同时考虑在位库仑修正对氧的p电子和过渡金属d电子的协同效应.因此，本文旨在同时考察Ti 3d轨道和氧的 2p轨道库仑修正，获得了与实验结果吻合的计算值.对于Rutile，Anatase和Brookite，设定Ud=8 eV，Up分别为 6 eV，4 eV，4 eV，计算得到的带隙值与实验值非常接近.而对于TiO2(B)，设定Ud值为4 eV，Up=4 eV，计算得到的带隙值为3.21 eV，与实验值3.22 eV 非常吻合.

另外，在此基础上，考察分析了它们的态密度和带结构，并通过计算导带底CBM和价带底VBM处的电子和空穴的有效质量，比较有效质量的结果表明，Rutile和Anatase中电子和空穴的迁移率比Brookite和TiO2(B)快，并且光激发载流子的迁移速率顺序为Anatase >Rutile>Brookite>TiO2(B), 表明Anatase的光催化效果最佳，这与实验结果一致.