中远距空空导弹五自由度弹道建模与仿真分析

李海军，王天然，牟俊杰，郑 文

(1.海军航空大学，山东 烟台 264001；2.北京军代局驻太原地区第一军代室，山西 太原 030009)

0 引 言

目前，海战场环境下如何提高制空作战能力是海军装备建设面临的重大问题，因海面环境对电磁波传输的多路径效应、海杂波对引战配合[1]的影响等因素，空空导弹对低空掠海飞行目标的拦截是世界各国遇到的一个难题[2].空空导弹拦截掠海目标命中率较低一方面是导弹性能的问题，同时也有作战方法不够科学的原因.因此，本文提出利用弹道仿真结果改进空空导弹拦截掠海目标的作战方法.

空空导弹拦截作战中，弹遇靶时刻的脱靶量、交会角、导弹姿态角等是影响导弹毁伤概率的重要因素.本文针对某型中远距空空导弹拦截低空掠海飞行巡航导弹的特点，采用C++语言进行了五自由度弹道仿真程序设计，为保持三自由度简单特征同时得到导弹姿态信息[3]，在质点运动学方程中加入闭环自动驾驶的传递函数，在三个平动方程里增加两个姿态自由度，即俯仰和偏航.模型对导弹质心运动、姿态角等参数进行仿真计算，并对仿真结果做出分析，用于指导空空导弹拦截低空目标的作战使用问题，从而进一步研究以提高空空导弹命中率.

1 坐标系及坐标转换

在建立弹道仿真模型之前，先定义本文用到的坐标系.为简化起见，类似巡航导弹、战术拦截导弹以及对地攻击导弹一般均可采用扁平地球模型，这时地球可看作惯性参考系[4].本文中用到的坐标系主要有：地球坐标系E、地面坐标系L、弹体坐标系B、速度坐标系V、视线坐标系O.详细坐标系定义可参考文献[5-6].

坐标系之间通过坐标转换矩阵建立相互联系[7]，A坐标系中向量x表示为[x]A，设矩阵[T]BA为坐标系A和坐标系B的转换矩阵，则有

[x]B=[T]BA[x]A.

(1)

本文对各坐标系间的转换矩阵不做详细推导，下文提到的坐标转换矩阵命名方式同上.在仿真中，转换矩阵的实际计算工作分配在各个模块中.

2 五自由度仿真模型

针对某型空空导弹战术特点，建立了五自由度弹道仿真模型，整体框图如图 1 所示.该仿真整合了空气动力学[8]、推进[9]、飞行控制[10]、制导系统[11]、弹体运动、导引头等模型.

图 1 五自由度弹道仿真模型总体框图

首先根据在目标模块、运动学模块获得的目标、导弹运动信息，在导引头模块中计算得到视线角，然后在制导模块中根据导引律计算导弹加速度，该加速度输入至飞行控制系统得到导弹迎角、侧滑角，在旋转模块中计算出导弹姿态角.由空气动力和推进模型得到导弹受到的气动力和推力，在运动学模块中，通过求解运动方程可计算出速率及飞行轨迹角.以上为一步仿真计算，满足终止模块条件时停止计算.下面将对各个模块进行简要说明.

2.1 目标模块

由于空中目标往往具有高机动性并能够采取规避动作，因此空空导弹目标模型一般比较复杂[12].本文以低空掠海飞行巡航导弹为拦截对象，巡航导弹的飞行轨迹基本固定，因此为简化模型，将目标动作局限于以速度vT恒速直线飞行.该模块输出目标速度、位移信息到导引头模块和运动学模块中进行处理.目标位置矢量sT可表示为

(2)

2.2 空气动力学模块

由于仿真导弹为轴对称型，故滚转方向对导弹受到的空气动力影响很小.通过飞行控制模块提供的气流角即迎角α和侧滑角β计算空气动力，并与推进模块的推力一起发送至弹体运动模块，用于求解牛顿方程.

升力系数CL，阻力系数CD与导弹迎角、马赫数、推进力有关，在仿真中通过对气动参数表采用内插法来计算.在体轴坐标系中表示为

(3)

(4)

速度坐标系与弹道坐标系之间的转换矩阵[T]BV完全由迎角α和侧滑角β确定.

2.3 推进模块

空空导弹一般采用固体火箭发动机，其推力计算公式如式(5)，将计算结果发送至弹体运动学模块.

(5)

falt=fp+SΔP.

(6)

2.4 弹体运动学模块

运动学模块是仿真过程的中心，该模块将综合各个状态变量，求解运动方程，计算导弹速度和飞行轨迹角χ,γ.首先，在速度坐标系中利用牛顿第二定律建立方程，然后引入扁平地球假设，推导出模拟姿态动力学的运动方程.

(7)

式中：mB为导弹质量；vB为导弹相对惯性系速度；fa，fp为空气动力、推力.利用欧拉变换转换到速度参考系中，得到矩阵方程

(8)

式中：[ΩVE]为速度坐标系V关于地球坐标系E的角速度矩阵.

速度坐标系中

(9)

将体轴坐标系的空气动力和推力转化到速度坐标系有

[fa+fp]V=[T]VB[fa+fp]B.

(10)

将地面坐标系的重力加速度转化到速度坐标系

[g]V=[T]VL[g]L.

(11)

由式(8)～(11)可得到

(12)

首次积分用到的[T]VL由初始飞行轨迹角确定.

结合上述公式，导弹质心位置sB可由式(13)求得.

(13)

2.5 飞行控制模块

利用积分和比例前馈来改变加速度反馈驾驶仪[13].加速度指令来自于制导模块，法向加速度和侧向加速度输入到飞行控制模块中，输出迎角、侧滑角至空气动力学模块以计算空气动力.以法向加速度(俯仰平面)为例，其自动控制流程如图 2 所示.

图 2 俯仰平面自动控制流程图

实际自动驾驶仪中，反馈信号来自于惯性导航中的加速度计，仿真时采用加速度计的理想测量值

(14)

2.6 制导系统

给定导弹和目标状态，制导系统生成飞行控制指令，从而操纵导弹击中目标[14].本文仿真采用的比例导航模型是空空导弹最常用的制导模型，加速度指令为

a=KvBωOEuv-g,

(15)

式中：K为比例系数；ωOE为视线参考系相对地球参考系的角速度；uv为速度vB的单位矢量.

2.7 导引头模型

导引头的目的是要建立并维持对目标的视线，STB是导弹到目标的位移矢量，uTB是单位位移矢量，则

(16)

在弹体坐标系中用矩阵形式表示为

(17)

位移矢量包含了导引头视线方位角φSB和高度角ϑSB的重要角度信息.ϑSB即为下文仿真分析的导引头波束擦地角.

2.8 旋转模块

由空动力学模块中计算得到的[T]BV和运动学模块中的[T]VL计算弹体相对地面的旋转矩阵[T]BL，得到

[T]BL=[T]BV[T]VL.

(18)

该矩阵包含了弹体的姿态信息，导弹旋转速率

ωBL=ωBV+ωVL,

(19)

式中：ωBV和ωVL分别由气流角、飞行轨迹角计算得到.

3 拦截仿真结果分析

本文仅研究五自由度弹道建模及仿真计算方法，利用C++进行了弹道拦截仿真程序设计，仿真有以下前提条件：

1)参照国外某型麻雀空空导弹气动及推力参数；

2)以空射、拦截掠海飞行巡航导弹为基本条件；

3)假定空空导弹中制导正常，导弹中末制导交班正常.

在上述条件下来计算弹道，可以得出发射高度、距离、载机速度、目标速度、目标机动、目标进入角度等参数与弹道轨迹、脱靶量、弹体姿态角、导引头波束擦地角的影响关系.根据巡航导弹的弹道特点，仿真试验以迎头攻击为基本条件，重点分析导弹脱靶量、弹体俯仰角以及末制导雷达开机时导引头波束角三个关键参数及其影响因素.

3.1 导弹脱靶距离分析

空空导弹的脱靶距离是判断导弹是否命中的主要指标[15].本文仿真采用比例导引法，导航增益即比例导引系数K是影响导弹脱靶距离的关键，选取合适的比例系数可以使拦截更加可靠，从而提高毁伤概率.

仿真实验1：假设载机和目标均以0.8马赫的速度迎头平飞，载机高度为2 000 m，目标高度为30 m，发射距离为15 km.对不同比例导引系数下导弹的脱靶距离进行仿真，仿真数据如表 1 所示，拦截弹道如图 3 所示.

表 1 导弹脱靶距离仿真结果

图 3 不同比例导引系数下的拦截弹道图

由表 1 仿真数据可以看出，比例系数越大，脱靶距离越小，交汇越可靠.由图 3 可以看出，较大的比例系数可以加快导弹的下行，对下方目标的敏感性更强.为探究原因，利用仿真数据绘制了四种情况下的法向加速度变化情况，如图 4 所示.

图 4 不同比例系数下的法向加速度变化图

由图 4 可看出，较小的比例系数提供的加速度指令较小，因此在垂直方向上对目标的响应能力较低，而在接近目标时需要加快下降拦截目标，损耗了导弹的机动性能.在真实条件下导弹会受到来自周围环境的各种噪声干扰，系数增益过高会导致导弹稳定性变差，这时应综合考虑导弹拦截精确性和稳定性，在保持导弹稳定的前提下，选择较高导航增益以增强导弹的机动性和准确性.

实际导弹一般采用变导引系数的导引方法，根据不同任务需求，导弹自动选择最优比例导引系数，在确保稳定的同时尽可能发挥导弹毁伤威力.本文中对仿真进行了简化，采用定比例导引，取K=4.

3.2 导引头波束擦地角分析

海战场环境下，空空导弹在对低空目标进行拦截时, 由于导弹的飞行高度较低，会面临较为严重的海面多路径效应，多径干扰对导引头雷达跟踪测角有较大影响，是造成空空导弹脱靶的重要原因之一.由于海面存在Brewster效应[16]，当雷达波束擦地角以Brewster角进入时多径反射波能量最小，可以降低多径效应对雷达导引头的影响.

仿真实验2：假设载机和目标均以0.8马赫的速度飞行，目标高度为30 m，末制导雷达为Ku波段某频率.对不同发射高度、发射距离下末制导雷达开机时刻波束擦地角进行详细仿真，仿真结果如图 5 所示.

从图 5 中可以看出：

图 5 导引头波束擦地角仿真结果

1)波束擦地角与发射高度有正相关关系，发射高度越高，擦地角越大；

2)发射距离越远，波束擦地角越小.

不考虑惯导和中制导指令误差以及噪声干扰带来的偏差，雷达波束中心始终指向目标，因此弹目高度差越大，距离越小时，雷达波束中心指向与海面的夹角越大，即波束擦地角越大，仿真与实际越接近，本文仿真结果与实际情况基本相符.在仿真实验2条件下，末制导雷达为Ku波段某频率，Brewster角应为9°左右.作战使用时可根据该角度确定雷达开机最佳擦地角，选择合适的发射高度和发射距离.例如由图5可知，发射距离为15 km时，发射高度在2 000～3 000 m比较合适.

3.3 导弹弹体俯仰角分析

在攻击掠海飞行目标时，导弹引信可能受海杂波影响，导致启动概率下降，或引信对水面错误启动导致早炸.当弹体倾角在某一范围内时，可构成引信波束垂直入射水面的条件，此时反射最强，对引信影响最大.因此，合理调整弹道使遇靶时弹体倾角避开此范围，可以降低海面对引信的干扰.

仿真实验3：假设载机和目标均以0.8马赫的速度迎头平飞，目标高度为30 m.对不同发射高度、发射距离下遇靶时刻弹体的俯仰角进行详细仿真，仿真结果如图 6 所示.

由图 6 仿真结果可以看出：

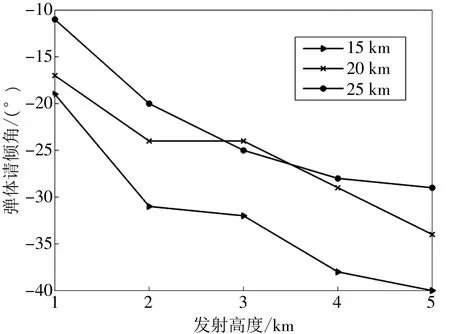
图 6 弹体俯仰角仿真结果

1)遇靶时刻弹体俯仰角随发射高度的变化具有正相关关系，发射高度越高，弹体倾角越大.

2)发射距离越远，弹体俯仰角越小.

在仿真实验2条件下，当弹目距离较近、高度差较大时，为拦截目标，导弹速度方向应向下且迎角较小，此时弹体倾角较大.以上仿真结果与实际情况基本相符，作战使用时可根据需求确定弹目最佳交会角，选择合适的发射高度和发射距离.

4 结 论

从上文的分析可以看到，导引系数、导弹发射高度、距离对导弹飞行弹道均有较大影响，可通过改变导弹发射高度、发射距离等发射条件达到最佳的导引头波束擦地角和弹体倾角以降低复杂的海面环境对雷达制导、引信起爆的影响，提高导弹对目标的毁伤概率.

其实，影响导弹弹道、姿态的还有弹目速度、导弹进入角、目标机动等诸多因素，以上仅对导引系数、发射高度、距离因素进行了分析，用以说明本文中提出的五自由度建模方法对导弹弹道、姿态信息均可仿真，仿真结果可用于作战指导，其他因素的仿真分析可在后续进行详细研究.

根据弹道仿真结果，在面临不同任务需求时可以通过控制发射条件获得雷达开机时最佳擦地角、弹目相遇时刻的最佳交会角，以降低海面多径效应、海杂波等因素对导弹的干扰.