“五育”并举引领高考数学应用题

◇ 山东 刘 进

高考数学命题贯彻德智体美劳全面发展的教育方针，倡导“五育”并举，这一命题原则在2020年高考数学应用题中得到了充分体现．在“五育”并举的引领下，全国卷数学命题紧贴“数学知识与生产、生活相联系”的要求，数学应用题可谓妙题生花、精彩纷呈．本文举例解析以“五育”为背景的高考应用题，旨在探索题型规律，供新一轮高考学生数学复习备考时参考．

1 以“德育”为背景的应用题

例1（2020年全国卷Ⅱ文4理3）在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1200份订单的配货，由于订单量大幅增加，导致订单积压，为解决困难，许多志愿者踊跃报名参加配货工作．已知该超市某日积压500份订单未配货，预计第二天新订单超过1600份的概率为0.05．志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单配货的概率不小于0.95，则至少需要志愿者（ ）．

A．10名 B．18名 C．24名 D．32名

解析

点评

本题是以抗击新冠疫情期间志愿者参加某超市配货工作为背景的应用问题，考查了考生对基本知识的掌握程度及运用所学知识解决实际问题的能力．

2 以“智育”为背景的应用题

A．60 B．63 C．66 D．69

例2（2020年全国卷Ⅲ文理4）Logistic模型是常用数学模型之一，可应用于流行病学领域，有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I（t）（t的单位:天）的Logistic模型:I（t）＝

解析

点评

本题以新冠肺炎疫情传播的动态研究为背景，选择适合学生知识水平的Logistic模型作为试题命制的切入点，考查学生对指数函数与对数函数基本知识的理解和掌握，以及使用数学模型解决实际问题的能力和数学建模、数学运算等核心素养．

例3（2020年新高考全国卷Ⅰ6）基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数．基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间．在新冠肺炎疫情初始阶段，可以用指数模型I（t）＝er t描述累计感染病例数I（t）随时间t（单位:天）的变化规律，指数增长率r与R0，T近似满足R0＝1＋r T．有学者基于已有数据估计出R0＝3.28，T＝6．据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为（ ）（ln2≈0.69）．

A．1.2天 B．1.8天

C．2.5天 D．3.5天

解析

由R0＝1＋r T，得3.28＝1＋6r，解得r＝0.38，所以e0.38t＝2，所以0.38t＝ln2，解得．故选B．

点评

本题基于新冠肺炎疫情初始阶段的研究成果，考查了相关的数学知识和从资料中提取信息的能力，突出了数学知识和数学模型的应用．

3 以“体育”为背景的应用题

例4（2020年新高考全国卷Ⅰ5）某中学的学生积极参加体育锻炼，其中96%的学生喜欢足球或游泳，60%的学生喜欢足球，82%的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的（ ）．

A．62% B．56%

C．46% D．42%

解析

由题意得，82%＋60%－96%＝46%．故选C．

点评

身心健康是素质教育的重要内容，高考数学设计了以体育运动为问题情境的试题，体现了积极的导向作用，本题以关注学生的体育运动与体育锻炼为背景，设计了简单的概率计算问题，考查了考生阅读理解和分析、转化能力．

例5（2020年全国卷Ⅰ理19）甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下．

累计负两场者被淘汰:比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束．经抽签，甲、乙首先比赛，丙轮空．设每场比赛双方获胜的概率都为

（1）求甲连胜四场的概率；

（2）求需要进行第五场比赛的概率；

（3）求丙最终获胜的概率．

解析

（1）甲连胜四场只能是前四场全胜，所以所

（2）根据赛制，至少需要进行四场比赛，至多需要进行五场比赛．

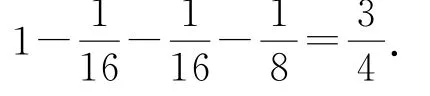
（3）丙最终获胜，有两种情况．

因此，丙最终获胜的概率为

点评

本题以羽毛球比赛为背景，将概率问题融入常见的比赛中，以参赛人的获胜概率设问，重在考查学生的逻辑推理能力、对事件进行分析、分解和转化的能力以及对概率的基础知识（特别是古典概率模型、事件的关系和运算、事件独立性等内容）的掌握情况．

4 以“美育”为背景的应用题

例6（2020年全国卷Ⅱ文3）如图1，将钢琴上的12个键依次记为a1，a2，…，a12，设1≤i＜j＜k≤12．若k－j＝3且j－i＝4，则称ai，aj，ak为原位大三和弦；若k－j＝4且j－i＝3，则称ai，aj，ak为原位小三和弦．用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为（ ）．

图1

A．5 B．8 C．10 D．15

解析

原位大三和弦:i＝1，j＝5，k＝8；i＝2，j＝6，k＝9；i＝3，j＝7，k＝10；i＝4，j＝8，k＝11；i＝5，j＝9，k＝12共5个；原位小三和弦:i＝1，j＝4，k＝8；i＝2，j＝5，k＝9；i＝3，j＝6，k＝10；i＝4，j＝7，k＝11；i＝5，j＝8，k＝12共5个．总共10个，故选C．

点评

借助数学语言给出原位大三和弦与原位小三和弦的定义，并设计了一个简单的计数问题，考查学生对新定义、新情境的学习能力，以及分析问题的能力和数学文化素养．

例7（2020年全国卷Ⅰ文理3）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥（如图2）．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（ ）．

图2

解析

如图3，设正四棱锥的高为h，底面边长为a，侧面三角形底边上的高为h′，依题意有

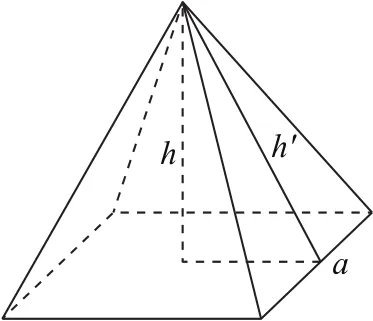
图3

点评

本题以世界建筑奇迹埃及胡夫金字塔为背景，设计正四棱锥的计算问题，将立体几何的基本知识与建筑文化有机结合，体现数学美和数学应用的广泛性．

5 以“劳动教育”为背景的应用题

例8（2020年新高考全国卷Ⅰ15）某中学开展劳动实习，学生加工制作零件，零件的截面如图4所示．O为圆孔及轮廓圆弧AB所在圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BC⊥DG，垂足为C，A到直线DE和EF的距离均为7cm，圆孔半径为1，则图中阴影部分的面积为________cm2．

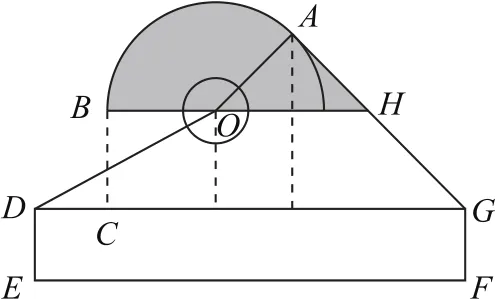
图4

解析

由已知得A到DG的距离与A到FG的距离相等，均为5，所以∠AOH＝45°．设O到DG的距离为3t，则O到DE的距离为5t，所以OAcos45°＋5t＝7，OAsin45°＋3t＝5，因此2t＝2，所以，所以图中阴影部分的面积为

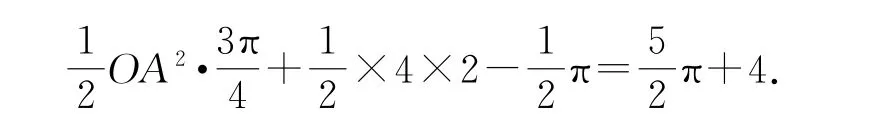
点评

本题通过创设一个劳动情境考查几何知识，同时培养学生的数学应用意识，提高学生对劳动实践的兴趣．高考数学将社会生产劳动实践情境与数学基本概念有机结合，很好地发挥了高考试题在培养劳动观念中的引导作用．