传承与创新 体会数学文化的应用价值——由一道费马点问题的命制过程谈数学文化的应用

黄腾达

（仙游县第二中学，福建 莆田 351200）

一、试题展示

问题：已知△ABC 的每个内角都小于120°，如何在三角形内部找一点P，使PA+PB+PC 的和最小？数学家们是怎样解决这个问题的？法国数学家费马是这样想的：如图1，将△APC 绕A 点逆时针旋转60°得到△AP′C′,则△APP′为等边三角形，PA+PB+PC=PP′+PB+P′C′ ≥BC′,当且 仅 当B、P、P′、C’四 点共线时取最小值。该点也称为这个三角形的费马点。小明同学在研究该问题时发现，若改变旋转角的度数，就可以产生aPA+PB+PC 的最值问题。

（1）如图2，已知△ABC 中，∠ACB=90°，AB=5,BC=3,P 为三角形内部一点。将△APC 绕A 点逆时针旋转90°得到△AP′C′,请画出△AP′C′，并求2 PA+PB +PC 的最小值。

（2）若P 为平面内的一点，过P 点引出三条线段：PA、PB、PC，若PA+PB+PC 为定值m,猜想△ABC 面积的最大值，并直接写出答案。

（3）如图3，已知：四边形ABCD 中，AB=AD=2，连接AC，求AC 的最大值。

二、设计过程

（一）命题意图

这是一道以数学文化为背景的考题，以阅读理解形式出现，结合相似三角形、锐角三角函数、勾股定理、图形的旋转、两点之间线段最短等知识，在渗透数学文化的同时考查学生的自学能力、综合运用所学知识解决实际问题的能力，检测学生的数学抽象、数学建模、逻辑推理和直观想象等学科素养。

学科核心素养的表现及其级别

（二）命题过程

1.立意与选材：各地中考以数学文化为背景的试题在难度的设置上大多为中等偏易，较少出现以数学文化有关的综合题。能否尝试命制以数学文化为背景的几何综合题，引领学生领悟其中蕴含的数学思想，体会数学文化的应用价值？需要选取什么素材？“求线段和差的最值问题”一直是中考命题的热门问题。初中教材中出现过借助轴对称求解的“将军饮马问题”，也出现过借助平移求解的“修桥定址问题”，若选取费马点问题恰好可以作为教材知识的补充和拓展，同时，费马点问题综合性强，蕴含着丰富的数学思想，能够比较全面考查学生的学科素养，发挥试题的选拔功能。［1］

2.联系与搭架：费马点问题，作为一个历史名题，近几年来在各地中考中也频频出现，如2010 宁德中考、2013 常州中考、2016 盐城中考等。例：（2010 宁德中考摘录）如图4，正方形ABCD 中，以AB 为边向外作等边△ABE，点M 是对角线BD（不含B 点）上一动点，将BM 绕点B 逆时针旋转60°得到BN，①当M 点在何处时，AM＋BM＋CM的值最小，并说明理由；②若AM＋BM＋CM 的最小值为+1 时，求正方形ABCD 的边长。

常州中考题与盐城中考题与这道题目类似，在条件中都预设了旋转的条件或者构造了等边三角形，借助全等三角形铺垫，引导学生发现三条线段的转化方法。这样，在对费马点问题改造的同时保留费马点问题的本质，同时降低入口的难度，呈现自然，思路顺畅，深入浅出，体现了命题者高超的命题技巧。那么他山之石如何借鉴？又如何创新？

3.加工与调整：能不能把问题反过来呢？在学校九年级数学课外兴趣小组的活动课上，笔者给同学们留下这样一道思考题：（第一稿）从平面上一点P 引三条线段PA、PB、PC，若PA+PB+PC=m，则△ABC 面积的最大值是__。

猜想：当且仅当P 为△ABC 的费马点，且PA=PB=PC 时，△ABC 的面积最大。此时△ABC 为等边三角形，面积为但是如何证明这个结论？

（1）考虑用代数法：如何构建函数模型或不等式模型？题目中的变量太多了，显然难度太大了，弃之！

（2）还是考虑用几何法：任取一点P，过P 点任意引出PA、PB、PC，设PA+PB+PC=m，得到△ABC。若点P 不是该三角形的费马点，设该三角形的费马点为D，则必有DA+DB+DC＜m.设则k＞1。如图5，以D 为位似中心，将△ABC 放大k 倍，得到△EFG，则 必 有DE+DF+DG=k（DA+DB+DC）=m,且S△EFG=k2S△ABC＞S△ABC。由此可知，点P 为△ABC 的费马点时，该三角形的面积最大。以下探究当PA、PB、PC 的长度各为多少时面积最大。

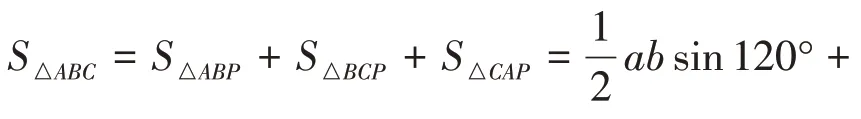
如图6，设点P 为△ABC 的费马点，且PA=a，PB=b，PC=c，且a+b+c=m。由已知可得：∠APB=∠BPC=∠CPA=120°，所以：因为a+b+c=m,故(a+b+c)2=a2+b2+c2+2ab+2bc+2ca=m2又a2+b2+c2≥ab+bc+ca，所以m2=a2+b2+c2+2ab+2bc+2ca≥3(ab+bc+ca)。

对于这道试题，学生反馈的信息是刺窝里摘花——无从入手。有个别学生猜出了问题的答案，但具体原因却说不清。主要原因是孤立地出现这个问题，学生很难联系与之相关的知识。但从另一角度看，这道题恰好可以考查学生直观想象的素养，有助于鼓励学生勇于猜想的思维品质。这串貌似触手可及的“葡萄”，驱动着他们积极地“跳跃”。

为了让问题的呈现更加自然，笔者对题目进行了改编。（第二稿）问题：已知△ABC 的每个内角都小于120°，如何在三角形内部找一点P，使PA+PB+PC的最小？数学家们是怎样解决这个问题的？法国数学家费马是这样想的：如图7，将△APC 绕A 点逆时针旋转60°得到△AP′C′,则△APP′为等边三角形，PA+PB+PC=PP′+PB+P′C′ ≥BC′,当 且 仅 当B、P、P′、C’四点共线时取最小值。该点也称为这个三角形的费马点。

如图8，在△ABC 中，AB=AC=6，P 为三角形内部一动点，且PA+PB+PC 的最小值是求此时线段PA 的长。

如图9，已知△ABC 中，∠ACB=90°，AB=5,BC=3,P为三角形内部一点，试求的最小值及此时线段PA 的长。

若P 为平面内的一点，过P 点引出三条线段：PA、PB、PC，若PA+PB+PC 为定值m,直接写出△ABC 面积的最大值。

通过把试题设计成阅读理解的形式，融入数学文化，让学生领悟数学家解决问题的方法，建立数学模型。而求费马点到三个顶点的距离之和的问题，实质上就是旋转后求解三角形的问题。第（1）问应用材料的方法，把△ABP 绕A 点逆时针旋转60°后，变成已知三边求解三角形的问题。第（2）问，只要把旋转角改成90°，就可以构建PA，从而进一步求解。对于第（3）问，有了（1）、（2）问的铺垫，学生容易猜想当点P 为三角形费马点，接着只要考虑PA、PB、PC 取何值面积最大的问题，降低了思考的难度。

试题分析：（1）问属于方法的直接运用，（2）问是（1）问的变式，但改变的只是旋转的角度，与材料中的问题变化不大，学生的解题基本上还停留在模仿的层面上，并没有实现从一个问题到一类问题的突破。（3）问由于只要直接写出答案，大大降低了难度，所以这道试题不能较好地考查出学生思维的深度。

费马点问题求解的实质，是借助于旋转构造全等三角形，［2］利用线段的等量关系，优化线段的位置，从而把共顶点的三条线段的最小值问题转化成两点之间线段最短的几何模型求解。［3］涉及的基本图形手拉手模型（如图10）。观察手拉手模型的基本图形，由△ABD 与△ACE 的全等（或相似），若已知线段AE、CE 的长度，即可求出线段AD、BD 的长度，再借助△ADE 和△ABC 的相似，进一步求线段DE 长度，从而可以求出BE 的最值。这样恰好与费马点问题的求解思路互逆，可以更好地看出学生对模型的理解程度。为了能体现方法普遍性，让学生体会这类问题的通法，故把△ABC 设置成一个一般的三角形，最终定稿为文初试题。

三、解答分析

解：（1）如图11，△AP′C′如图所示。

连 接BC′、PP′,C′D ⊥BC,交BC延长线于点D，则当且仅当B、P、P′、C’四点共线时最小。

由已知可得：四边形ACDC′为正方形

（3）如图12，作DF⊥BC于F，连 接BD，作∠EBC=∠ABD、∠ECB=∠ADB,连 接AE。设DC 的长度为2k，则BC=3k。

∵∠DCB=60°

∵∠EBC=∠ABD ∠ECB=∠ADB

∴△ABD∽△EBC

∵∠ABD+∠DBE=∠EBC+∠DBE

即∠ABE=∠DBC

四、试题评析

试题提供费马点问题的相关材料，在介绍问题的背景的同时提供了解决共顶点的三条线段求和的最值的方法。让学生在阅读理解的基础上抽象出数学模型，考查学生数学建模和数学抽象的核心素养。问题分三个层次，（1）问通过作图的预设，降低了难度，求解过程只需模仿材料提供方法即可，（1）问的设置面向全体，旨在完成达到下要保底的目标。（2）问鼓励学生大胆猜想，考查直观想象能力。猜出答案并不困难，但要得出其中的原因却不易，期待学生能在课后延续问题的思考，体会“猜想—论证—再猜想—再论证”的科学探究方法。（3）问是方法的应用和拓展，考查学生对模型的理解程度，融入相似三角形、勾股定理、基本图形的构造等，考查学生的逻辑推理的学科素养。总之,整道试题层次鲜明，综合性强，以学科核心素养为导向，突出对四基四能的考查，注重学生的创新意识，同时试题中蕴含着数学文化背景，引导学生关注数学文化。

五、命题拓展

（一）第（1）问的拓展与变式：

1.如图13：△ABC 中，设AB=m,AC=n,∠BAC=β,对于任意给定的满足条件的正实数a,aPA+PB+PC 的最小值问题可以先将△APC 绕A 点逆时针旋转一个特定的角度θ，得到△AP′C′,使PP′=aAP，当且B、P、P′、C’四点共线时aPA+PB+PC 取最小值。

（1）旋转角θ 由图中的△APP′确定，满足cos θ=θ 应满足θ+β ＜180°。

（2）实数a 应满足条件受到△APP′存在条件限制和（1）中旋转角的限制，θ+β ＜180°⇒＜90°-

（3）aPA+PB+PC 的最小值可以在在△ABC′中求解。结论为：

2.如图14，△ABC中,设AB=m,AC=n,∠BAC=β，对于满足条件的正实数a、b，要求aPA+bPB+PC的最小值，可以先将△ABP 绕A 点顺时针旋转一个特定的角度θ，得到△AB′P′,再以A 为位似中心，将△AB′P′放缩成原来的b 倍，得到△AB″P″,其中PP″=aPA,PB,P″B″=bPB,故当且仅当B″、P″、P、C 四点共线时，aPA+bPB+PC 有最小值，最小值即线段B″C的长。

（2）实数a、b 应满足条件受到△APP″存在的限制和（1）中旋转角的限制。具体为：a+b ＞1且-1 ＜a -b ＜1且1+b2-a2+2bcsoβ ＞0。

（3）aPA+bPB+PC 的最小值可以在△AB″C 中求解。结论为：

3.aA+bPB+cPC 型的最小值问题只需提取系数c，即可转化成上面双系数型的方法求解。

（二）第（2）问中蕴含的不等式：

2.ab sin α+bc sin β -ac sin(α+β)≤(a+b+c)2（其中a、b、c 为正数，0 ＜α、β ＜180°），当且仅当a=b=c 且α=β=120°取等。

（三）第（3）问的拓展：

如图15，△ABC 中，BC:AC:AB=a:b:c，D 为平面内一点，且DB=m，DA=n。由（3）问证明可知，当∠ADB+∠ACB=180°时DC 有 最 大值。此时A、B、C、D 共圆，由托勒密定理可得DC 最大值为：

六、命题反思

试题不足之处：费马点作为一个拥有300 多年历史的名题，吸引着无数数学爱好者的目光，相关的研究成果可汗牛充栋。故以该题材为背景的试题，总感觉新意不足，摆脱不了套题的嫌疑。但个人认为：一道试题，在考查知识方法的同时，能够引导学生去领悟数学的思想方法，激起学生追根溯源的探知欲望，就是一道好的试题。

新课程标准明确要求，要把数学文化融入到数学的学习内容中去，充分体现数学的文化价值。近年来，以数学文化为背景的试题己成为中考命题的新亮点。在数学文化试题的命制过程中，我们要深入挖掘素材里蕴含的数学思想和数学方法，通过合理的设计，让学生能尽可能地体会数学文化的科学价值和应用价值，感受数学文化的博大精深和无穷魅力。