在数控铣床上加工链轮齿形
■ 河北省迁安市首钢矿山机械制造厂 (河北迁安 064404) 秦 涛
链轮是常见的零件之一,因应用场合不同,其齿形大小、齿数等各不相同,但其齿形与节距是标准的,齿形最常见的就是“三弧一线”标准齿形,齿形的各个参数在设计手册中能够查到。图1所示为标准的“三弧一线”链轮齿形,牙形关于Y轴左右对称,图中标识了工件坐标系的X、Y轴原点,Z轴原点在链轮齿形上端面。
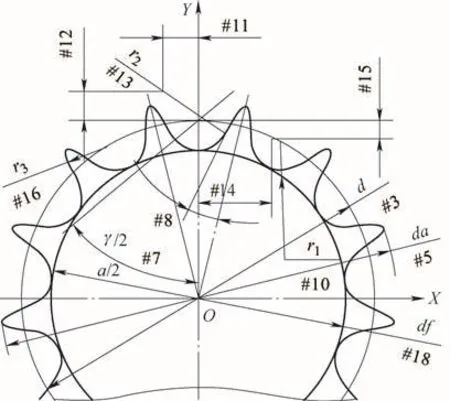
图1 牙形示意及参数
1. 刀具路线与编程思路
编写一个齿形的加工程序,其他齿形采用坐标系旋转的方式加工,齿形的总厚度(Z轴厚度)采用变量进行加工,每刀进给0.3~0.8mm,可根据加工需要选择。刀心轨迹及与齿形轮廓对应点如图2所示,从A点到G点,每个点与齿形轮廓上各交点都是对应的,刀心的轨迹始终相对于齿形轮廓偏移一个铣刀半径值。
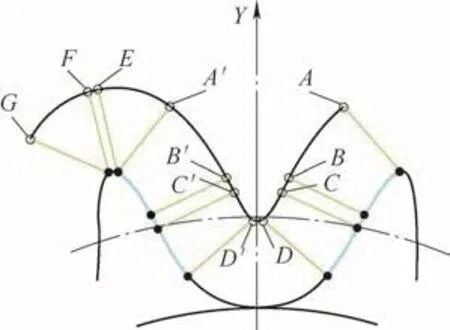
图2 刀心轨迹
2. 程序编制
操作人员接到加工任务,拿到图样,把图样中链轮齿数#1、链滚子直径#2、分度圆直径#3、链轮外径#5、齿形厚度#6、刀具直径#32这6个参数赋值到程序中。程序中的计算方法及技巧,具体解释及说明如下。
G54G17G40G69M3S2000F1000
#1=13;链轮齿数。
#2=8.51;链滚子直径。
#3=52;分度圆直径。
#5=58;链轮外径,赋值时比图样尺寸加1mm。
#6=-10;齿形厚度,也就是Z轴的终点尺寸。
#32=4;铣刀半径。
IF[#1LT11]GOTO10;
IF[#1LE17]GOTO15;
IF[#1LE35]GOTO20;
IF[#1GT35]GOTO25;
N10 #4=0.58;
GOTO50;
N15 #4=0.56;
GOTO50;
N20 #4=0.53;
GOTO50;
N25 #4=0.5;
GOTO50;#4是K系数的赋值,K系数的对应值与链轮齿数有关,齿数<11为0.58,齿数11~17为0.56,齿数17~35为0.53,齿数>35为0.5,这几段程序可以自动选择K系数值,每次加工不同齿数的链轮齿形时不需要手动查询改写#4参数。
N50#7=[55-60/#1];齿沟半角,公式来自工具书。
#8=[17-64/#1];齿形半角,公式来自工具书。
#9=[18-56/#1];工作段圆弧中心角,公式来自工具书。
#10=0.5025*#2+0.05;齿沟圆弧半径r1,公式来自工具书。
#11=-0.8*#2*SIN[#7];工作段圆弧中心O2的X轴坐标,公式来自工具书。
#12=0.8*#2*COS[#7];工作段圆弧中心O2的Y轴坐标,公式来自工具书。
#13=1.3025*#2+0.05;工作段圆弧半径r2,公式来自工具书。
#14=1.3*#2*COS[180/#1];齿顶圆弧O3的X轴坐标,公式来自工具书。
#15=-1.3*#2*SIN[180/#1];齿顶圆弧O3的Y轴坐标,公式来自工具书。
#16=#2*[1.3*COS[#8]+0.8*C OS[#9]-1.3025]-0.05;齿顶圆弧r3半径,公式来自工具书。
#18=#3-#10*2;齿根圆直径,在机床查到此值用于检测工件。
参数#11、#12、#14、#15坐标原点在r1的圆心上(见图1)。计算A点坐标的图解如图3所示,程序如下。
#19=SQRT[[#14*#14]+[#3/2+#15]*[#3/2+#15]];r3圆心O3点到工作坐标原点的距离,根据O3点的坐标和分度圆的半径解直角三角形求斜边#19。
#20=A C O S[[#16*#16+#19*#19-#5/2*#5/2]/[2*#16*#19]];使用余弦定理计算角度。
#115=SQRT[[#16+#32]*[#16+#32]+#19*#19-2*[#16+#32]*#19*COS[#20]];使用余弦定理,计算点A所在直角三角形的斜边长度。
#21=ASIN[#14/#19]-ASIN[[#16+#32]*SIN[#20]/#115];使用正弦定理计算角度。
#22=SIN[#21]*#115;A点X轴坐标。
#23=COS[#21]*#115;A点Y轴坐标。
计算B点坐标的图解如图4所示,程序如下。
#24=#8+180/#1;利用外角等于两内角和公式计算。
#2 5=#1 4-C O S[#2 4]*[#16+#32];B点X轴坐标。
#2 6=#3/2+#1 5+S I N[#2 4]*[#16+#32];B点Y轴坐标。
计算C点坐标的图解如图5所示,程序如下。
#2 8=C O S[#2 4]*#1 3+#11-COS[#24]*#32;计算C点X轴坐标。图5中两个“#24”虽不是同一个位置的角度,但大小相等,因为从C点连接齿形直线段下端点是垂直关系,O3点连接直线段上端点也是垂直关系。
#2 9=#3/2+S I N[#2 4]*#3 2-[SIN[#24]*#13-#12];C点Y轴坐标。
计算D点坐标的图解如图6所示,程序如下。
3)在体育舞蹈传授过程中,让学生懂得体育舞蹈赛事组织,学习体育舞蹈基本礼仪,促使学生相互沟通,增进友谊,增强自信心,丰富大学生的社会文化生活。
#30=SIN[#7]*[#10-#32];D点X轴坐标。
#31=#3/2-COS[#7]*[#10-#32];D点Y轴坐标。
#100=0;Z轴切削的起始点。
#101=#6;#6赋值给#101。
计算E点坐标的图解如图7所示,程序如下。
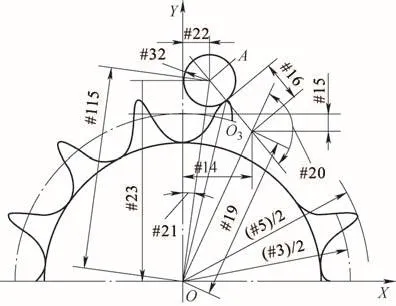
图3 计算A点坐标图解
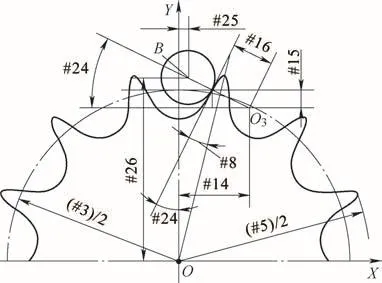
图4 计算B点坐标图解
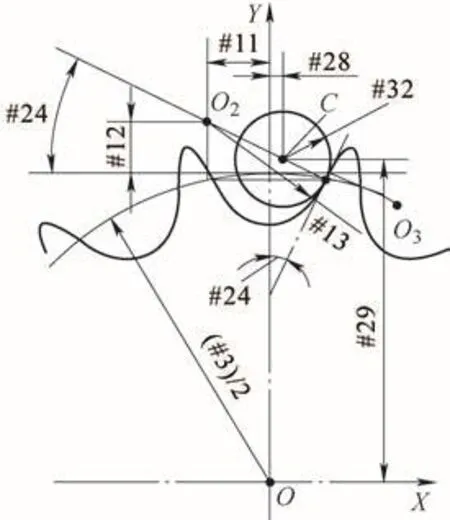
图5 计算C点坐标图解
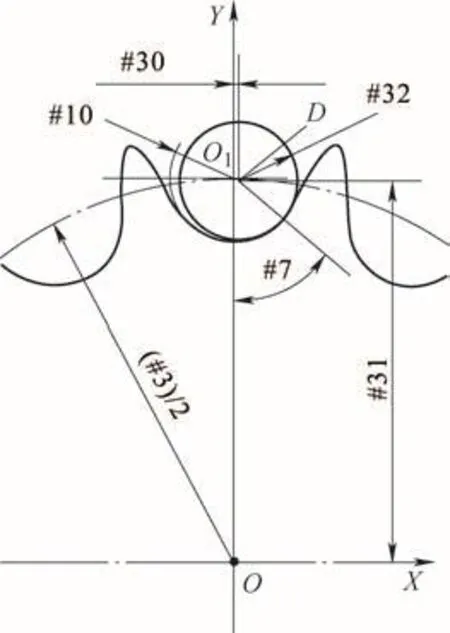
图6 计算D点坐标图解
#102=ACOS[[#115*#115+#5/2*#5/2-#32*#32]/[2*#115*#5/2]]+#21;连接EO,利用余弦定理计算该线段与Y轴的角度,E点是齿顶右端的对应点。
#103=-SIN[#102]*[#5/2+#32];E点X轴坐标。
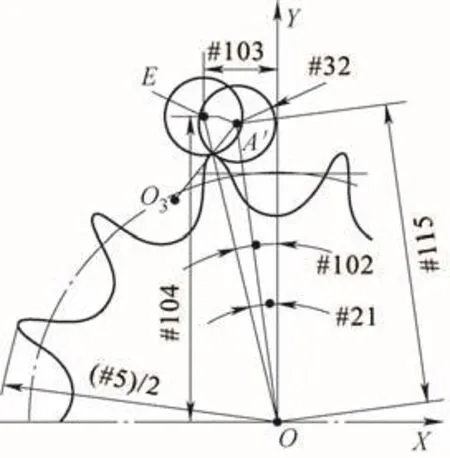
图7 计算E点坐标图解
计算F点坐标的图解如图8所示,程序如下。
#106=360/#1-#102;左侧第2个齿形旋转角度为360/(#1),利用图7计算的#102就很容易计算#106,F点是齿顶左端的对应点。
#107=-SIN[#106]*[#5/2+#32];F点X轴坐标,负值。
#108=COS[#106]*[#5/2+#32];F点Y轴坐标。
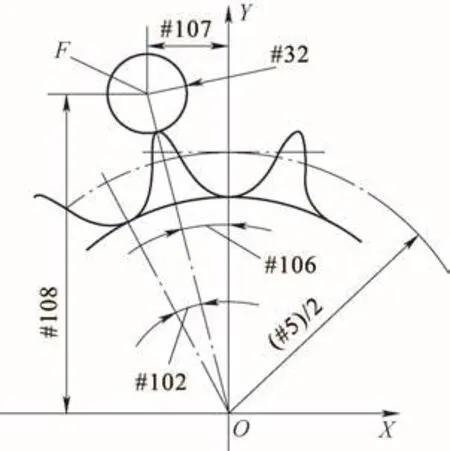
图8 计算F点坐标图解
计算G点坐标的图解如图9所示,程序如下。
#110=360/#1-#21;G点相对于图3中的A点旋转角度为360/(#1),利用图3计算的#21可直接计算#110。
#111=-SIN[#110]*#115;G点X轴坐标。
#112=COS[#110]*#115;G点Y轴坐标。
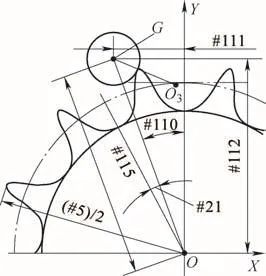
图9 计算G点坐标图解
到此为止,各个点就计算完成了,因齿形左右对称,左半部分对应的点不需要计算,编程是X轴取负值。
G0Z100;
IF[#32GE#10]GOTO100;如果铣刀半径不小于齿沟圆弧半径,程序执行直接跳转到程序结束,是质量保护程序段。
X0 Y[#5/2+#32];快速到达起始点,刀尖到工件外径有0.5mm的距离,工件定位根据具体情况确定,可采用心轴加压板式或采用自定心卡盘夹紧定位。
Z5;
WHILE[#100GE#101]DO1;循环语句,判断Z轴是否到达终点。
#109=0;坐标系旋转的初始角度。
G1Z#100;Z轴下降。
WHILE[#109LT360]DO2;循环语句,判断坐标系旋转是否到一周。
G 6 8 X 0 Y 0 R#1 0 9;坐标系旋转。
G1X#22Y#23;刀心走到A点。
G3X#25Y#26R[#16+#32];刀心走到B点。
G1X#28Y#29;刀心走到C点。
G2X#30Y#31R[#13-#32];刀心走到D点。
G2X-#30R[#10-#32];刀心走到D点。
G2X-#28Y#29R[#13-#32];刀心走到C点。
G1X-#25Y#26;刀心走到B点。
G3 X-#22Y#23R[#16+#32];刀心走到A点。
G3X#103Y#104 R#32;刀心走到E点,此段程序刀具没有实际切削,刀具只作了一个“绕”的动作,必须以圆弧半径#32来“绕”,而不能以直线方式走到下一个点。
G3X#107Y#108 R[#5/2+#32];刀心走到F点,没有实际切削。
G3X#111Y#112 R#32;刀心走到G点,也是下一个齿的起始点。
#109=#109+360/#1;坐标系旋转累加一个齿的角度。
END2;
#100=#100-0.5;Z轴每层下降0.5mm。
G1G69;取消坐标系旋转。
X0 Y[#5/2+#32];执行完整个坐标系旋转后,为下一个齿形起点做准备。此处不能使用G0。
END1;
N100 G0Z100;
M5;
M30;
——小学语文阅读教学中使用工具书的指导

