基于K-means 聚类分析的汽车行驶工况构建

周溪召，刘启超 （上海理工大学 管理学院，上海200093）

ZHOU Xizhao, LIU Qichao(School of Management, University of Shanghai for Science & Technology, Shanghai 200093, China)

0 引 言

汽车行驶工况是在特定交通环境下描述汽车行驶的速度—时间曲线，能够体现汽车道路行驶的运动学特征。目前NEDC、FTP-75 和Japan10-15 这三种标准工况被使用的频率最高，近年来我国学者也对此有所研究。苗强等[1]采用马尔可夫链构建济南市公交行驶工况，刘子谭[2]改进了K 均值聚类算法构建广州市汽车工况，李孟良等[3]采集了北京、上海和广州车辆行驶速度等运动学特征，生成3 个城市的工况并与ECE15 工况相比较，说明中国城市行驶工况的特点。本文利用主成分分析及Kmeans 聚类方法，在划分运动学特征时选取多个特征参数全面考虑，构建出一条汽车行驶工况，该方法同样可用于构建其他区域工况。

1 问题描述

研究构建符合中国地区交通特征的行驶工况，对于定量分析该地机动车燃料消耗水平、排放总量及控制水平从而制定相应的控制策略，具有重要的指导意义。本文将利用聚类分析方法探索构建地区汽车行驶工况。

2 算法解析

2.1 主成分分析

主成分分析是将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法，设原始数据有p维，用Y表示，若共有n个短行程，则Y｛Y1,Y2,…,YP｝n×p。主成分分析就是将p维数据降为k维X｛X1,X2,…,XK｝，这些数据能够充分反映原参数信息并相互独立，之后再对k维数据进行片段分析。数学模型式如下：

满足约束条件：

①li1+li2+…+lip=1，其中i=1,2,…,p。②Xi与Xj相互无关，i≠j,i,j=1,2,…,k。③X1是Y1,Y2…YP一切满足①的线性组合中方差最大的向量，同理Xk是与X1、…Xk-1均无关的Y1,Y2…YP所有线性组合中方差最大的向量。

那么X1、X2…Xk为原数据Y的第一主成分、第二主成分、第K主成分。

2.2 K-means 聚类

K-means 是基于划分的聚类算法。即给定n个数据点｛x1,x2,…,xn｝，设置k个聚类中心｛a1,a2,…,ak｝。利用欧几里得距离公式，计算每个点到中心点的距离，将点分到距离中心点最近的簇中；计算每个簇的平均值作为新的聚类中心；重复以上过程直到聚类中心不发生变化。欧几里得距离公式如下：

3 行驶工况构建

选择大连市某轻型汽车实际道路行驶采集数据进行研究，通过装在车上频率为1HZ 的GPRS 数据采集仪获取一周内车辆运行数据，得到的参数内容包括：时间、车辆速度、转轴加速度、瞬时油耗等。

3.1 运动学片段划分

将实际的车速曲线分割成多个时间的运动学片段，定义一个片段为汽车由静止启动的时刻开始，到下一次由静止启动的时刻结束。因此运动学片段描述车辆由加速、减速、匀速、怠速四个阶段组成的一个行驶循环周期。具体如图1 所示。为详细描述片段内的瞬时特征，根据速度v和加速度a将行驶状态划分为以下四种工况：①怠速状态：v=0m/s，发动机仍处于工作状态；②加速状态：v＞0m/s,a＞0.1m/s2；③减速状态：v＞0m/s,a＜-0.1m/s2；④≤0.1m/s2且v＞1m/s。

对采集到的数据进行小波变换预处理后共计341 872 组数据，根据上述行驶状态的分类标准，利用Matlab 编程，共划分运动学片段560 个。选取运动学片段特征参数，根据已有参考文献[4]本文定义9 个车辆运行特征参数和12 个片段统计分布参数，分别为运行时间T、平均速度vm、行驶速度vmr、速度标准差vsd、最大加速度amax、加速段平均加速度aa、最小减速度amin、减速段平均减速度ad、加速度标准偏差asd、0～10km/h 速度区间比例P0-10、10～20km/h 速度区间比例P10-20、20～30km/h 速度区间比例P20-30、30～40km/h 速度区间比例P30-40、40～50km/h 速度区间比例P40-50、50～60km/h 速度区间比例P50-60、60～70km/h 速度区间比例P60-70、大于70km/h 比例P＞70、加速工况时间比例Pa、减速工况时间比例Pd、匀速工况时间比例Pc、怠速工况时间比例Pi。采用Matlab 计算21 个特征参数的值可得到如表1 所示的运动学片段特征参数矩阵X560×21。

图1 运动学片段示意图

3.2 主成分分析结果

为消除上述特征参数间的相关性，同时简化问题分析，利用SPSS 对上述特征参数进行主成分分析。各主成分贡献率及累计贡献率计算按式（3）、式（4） 进行。根据已有的参考文献论述，从理论上讲，进行主成分分析时选取累计率超过80%的前几个主成分即可[5]，同时特征值若小于1，说明该主成分的解释力度还不如直接引入一个原变量的解释力度大，因此标准在于特征值大于1[5]。通过表2 可以看出前5 个主成分的累计贡献率为81.748%，各成分特征值都达到1，进一步对560 个运动学片段分析得到以主成分p1～p5为新参数的得分矩阵Y560×5，如表3 所示。

式中：λk为第k个主成分的特征值；φk为第k个主成分贡献率；ψp为前p个主成分的累计贡献率。

表2 主成分分析贡献率

表3 p1～p5 主成分得分矩阵

3.3 K-means 聚类结果

以所选的五种主成分为分析因子，根据主成分得分矩阵借助Matlab 工具包对560 个运动学片段聚类，将原来的运动学片段划分为3 类，筛选不必要的片段数，共计有效片段数401 个，根据表4 聚类结果可以看出运行时间、平均速度是聚类最主要的特征参数。根据每一类运动学片段的整体统计分布特点可以将所有运动学片段分为低速、中速、高速三大类，对于这三类中所有片段的21 种特征参数的平均值进行比较可以得到每一类运动学片段表现出的车辆行驶特征，得到如下结论：

表4 运动学片段聚类结果

（1） 第一类运动学片段怠速比例最高，平均行驶速度仅为9.715km/h，最大加速度和最小加速度等值都是三类中最小的，这代表车辆加减速频繁，行驶在交通堵塞严重的道路上，属低速行驶状态。（2） 第二类运动学片段怠速时间比相对较小，平均速度处于中等水平，最大加速度和最大减速度都是三类中的最大值。说明该路段比较畅通，车辆在该路段行驶时经常加减速，属中速行驶状态。（3） 第三类运动学片段加减速比例较大，怠速时间极少，平均速度最大，车辆行驶时保持匀速运行时间最长，说明该路段非常畅通，且车速可以保持在一个较高的范围内，属高速行驶状态。

3.4 工况合成

根据聚类分析结果，将同一类中随机选取的不同片段组合，构成大于1 200s 的路况，当随机筛选的速度时间曲线数据内平均速度误差在此类所有片段的速度±10%区间内浮动时，即可将此组速度时间曲线作为此类路况的代表工况。

第一类行驶工况平均速度为9.123km/h，筛选后由11 个片段组合而成计算平均速度为8.7035km/h，总体速度偏差为4.61%。第二类行驶工况平均速度为28.079km/h，筛选后由6 个片段组合而成，计算平均速度为26.8712km/h，总体速度偏差为4.49%。第三类行驶工况平均速度为38.167km/h，筛选后由9 个片段组合而成，计算平均速度为35.8840km/h，总体速度偏差为6.36%。

最终合成的工况需包含每一类片段库中的运动学片段，根据式（5） 计算每一类运动学片段在最终工况曲线中的时间占比。合成以单个运动学片段为基础构建1 285s 行驶工况，如图2 所示，此行驶工况共由11 个三类不同工况构成，其中一类工况5个，二、三类工况均为3 个，一类中运动学片段持续时间占据片段总时间的32.70%，二类中运动学片段持续时间占片段总时间的51.41%，三类中运动学片段持续时间占据片段总时间的15.89%，各速度段时间分别为420s、790s 和75s。

式中：Tk是k类片段在最终工况曲线中的时间占比，%；Ti,k是k类片段库中第i个片段的持续时间，s；Tf是设定的最终循环工况的运行时间，s。

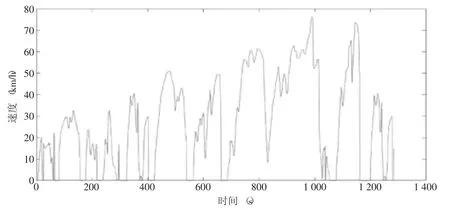
图2 汽车行驶工况图

4 构建评价

将本文构建的工况行驶状态特征参数与预处理后的原始数据特征参数作对比。由表5 中所得出的数据可以看出，所构建的道路行驶工况与其所在的采样总体绝对误差最大的是标准速度偏差，为18.93%，认为工况数据具有合理性。所构建工况与采样总体的相对误差在p60-70与p＞70上出现远超其他特征参数相对误差的值，分别为32.72%和29.75%，但由于其在整个采样总体中所占的比例仅仅为6.53%和1.22%，所以即使相对误差大，但是数据依然可信。除去p60-70与p＞70的数据后，其平均相对误差在13.87%，小于15%。综上所述，本文所构建的城市道路工况的道路行驶工况合理。

表5 初始数据与本文工况运动特征参数对比

5 结 论

本文将实验采集数据进行处理，构建行驶工况过程考虑的运动特征参数和统计特征参数全面，为后续分析提供了更详尽的统计；利用主成分分析法重新组合了21 个特征参数，重新构建了相互独立的主成分，此方法极大地减少了数据分析指标的维度，提高了数据分析速度和效率，该方法同样可用于构建其他城市行驶工况，但本文仅用运动特征参数构建了行驶工况并未对采集数据中的瞬时油耗等参数进行分析，因此可对轻型汽车的运行油耗做进一步研究。