A*与蚁群算法在火灾逃生中的应用分析*

程鹏举，孟凡坤，李 爽，吴 楠

（1.中国人民解放军战略支援部队信息工程大学，河南 郑州 450000；2.郑州大学，河南 郑州 450000）

0 引言

随着国民经济和科技水平的提高，城市的建筑规模不断扩大。其中，高层建筑和大型场馆结构复杂，人员密集。发生火灾时，现有的消防设备不能根据火灾实时情况进行相应的改变，可能会使逃生人员跑向火灾处。因此，探索火灾情况下智能有效的逃生指引，减少人员损失，具有重要的研究价值[1]。如何智能有效地引导人员逃生，涉及到路径规划问题。因此，本文主要探讨两种路径规划算法在火灾逃生路径规划中的应用及特点。

路径规划的方法有很多，主要有Dijkstar 算法、A*算法、蚁群算法和神经网络算法[2]，其各自的特点都不相同。文献[3]采用SEE 路径规划算法综合考虑火灾逃生路径的剩余长度和时间。文献[4]针对火场信息改进双向蚁群算法，动态规划路径。文献[5]结合网络流优化和改进的自适应果蝇算法，实现了节点和逃生路径容量有限的动态疏散路径规划。文献[6]采用正反向搜索交替机制改进A*算法，缩短了寻路时间。以上研究中，对算法和模型的改进一定程度上可以提高路径规划的效率，但算法固定单一，未分析算法在不同环境中的性能。因此，本文重点对A*算法和蚁群算法在不同火灾环境下的结果进行对比分析，从而为合理选用两种算法提供参考。

1 环境地图建模

本文采用栅格法对火灾逃生的建筑物环境进行建模[7]。为了突出两种算法性能的差异，简化其建筑物模型。假设各个楼层之间的消防楼梯通道安全，且各个楼层仅通过此处相互连接，故将整体的三维路径规划拆分为各个楼层的二维平面路径规划。对各楼层采用栅格法建模，其中可通行区域设为自由栅格，障碍物区域设为障碍栅格，发生火灾的区域设为火情栅格，而障碍物和火情不足一格的区域按照一个栅格计算，模型如图1 所示。此外，定义环境障碍阈值为障碍及火情栅格的总和与环境规模的占空比。

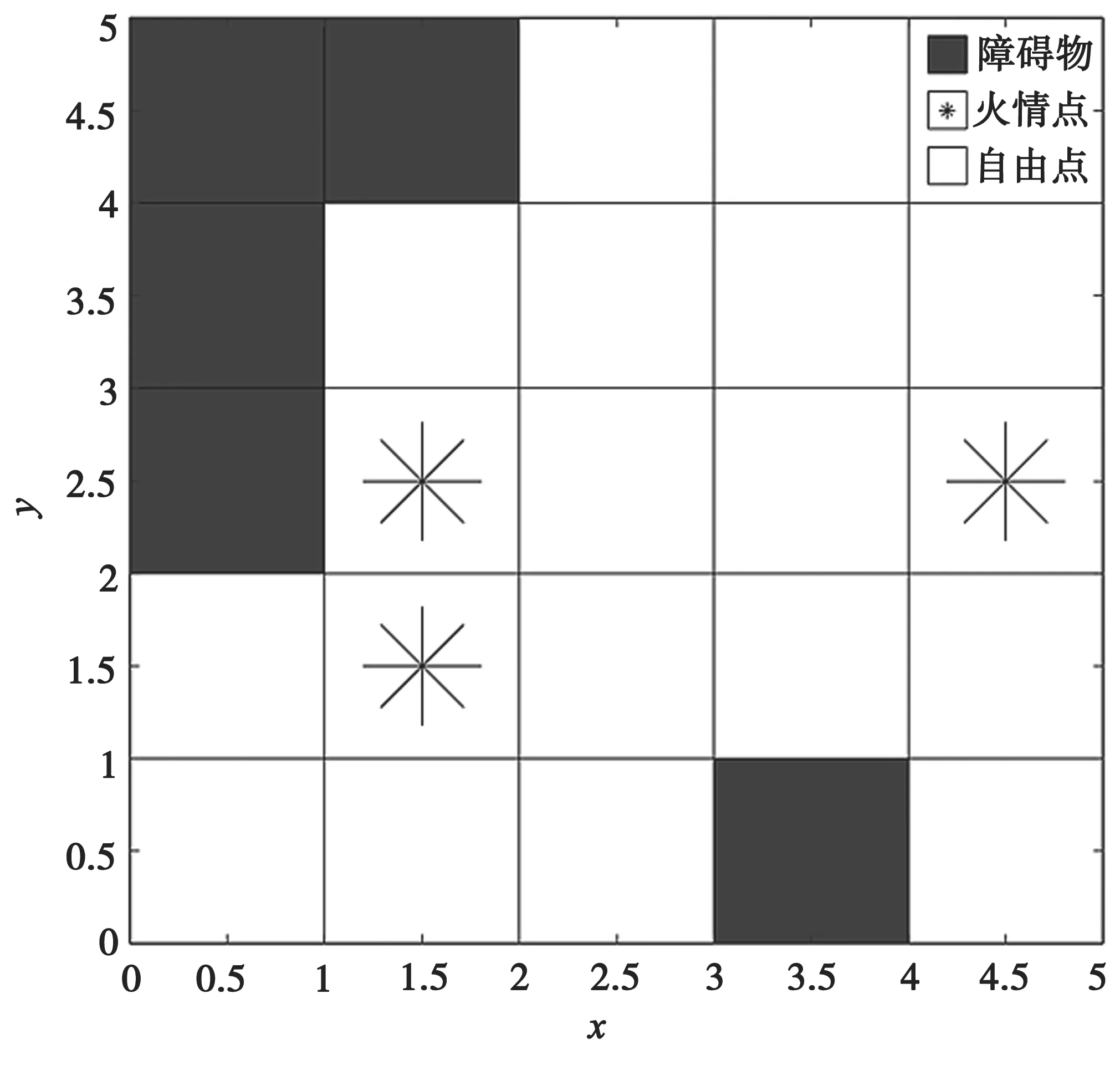
图1 环境栅格

将二维平面均匀划分为N×N的栅格地图，Ni={1,2,3,…,N2}为栅格序号集，按照从左至右从下至上依次编排。记i为任意栅格，其在xoy中对应坐标为(xi,yi)。定义左下角第一个栅格中心坐标为(0.5,0.5)，每个栅格中心坐标(xi,yi)与序号i构成如式（1）的映射关系[8]：

式中，mod 为求余运算，ceil表示向后取整数。

本文暂且只讨论单起点单终点情况，而多起点多终点规划可通过设置不同的起止点多次运行得到。其中，假设人员在逃生时的运动模型如图2所示，即人员每次只能在8 邻域栅格内移动一格。

图2 运动邻域模型

本文忽略人流密度、人员心理情绪以及火灾现场烟雾等影响因素，并假设人员的平均逃生速度为单位速度，栅格长度为单位长度。在火灾逃生中，时间就是生命，故构建以时间为标准的逃生安全代价函数式（2）：

式中：φ(t)表示安全通行所需的整体时间代价；ta表示算法耗费时间；L为规划出的路径长度，当规划不出路径时，L=∞；v为人员通行的平均速度。为简化计算，忽略人员逃生时转弯的时间消耗。

2 算法原理

2.1 A＊算法原理

A*算法由Peter E H 等人于1968 年提出，通过对相邻节点计算代价值，在进行启发式搜索提高效率的同时找到一条优化路径[9]。算法首先从起点开始，依次对8 邻域可通行节点计算启发代价，直到找到终点或进入死胡同或遍历完所有自由节点[10]。启发函数为：

其中，g(n)是从起点S到节点n的实际代价；h(n)是从节点n到终点T的估计代价；f(n)为节点n的代价函数。

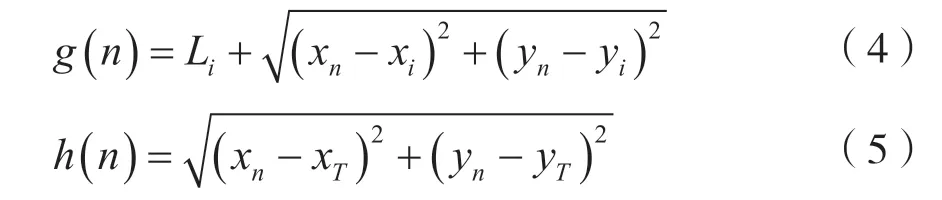
式中，Li是起点S到当前点i的实际代价，xn、yn是节点n的横纵坐标值，xi、yi是当前点i的横纵坐标值，xT、yT是终点T的横纵坐标值。设立集合C用于存储已经走过的节点，使其不被再次搜索。算法流程如图3 所示。

图3 A*算法流程

2.2 蚁群算法原理

蚁群算法是模拟蚂蚁觅食设计的仿生算法。蚂蚁在觅食时，会在其经过的路径上分泌信息素，并感知该路径信息素浓度，指导其运动方向[11]。蚂蚁的搜索过程如下。

在初始时刻，设将K只蚂蚁放在起点，各路径的初始信息素相等，为τij(0)=τ0。在t时刻，蚂蚁k从点i转移到点j的状态转移概率(t)为：

式中：ak为下一步可选节点的集合；τij为路径(i,j)上的信息素浓度；α为信息素权重；β为启发因子权重；ηij为点i到点j的启发因子，一般为两点间距离的倒数[12]。

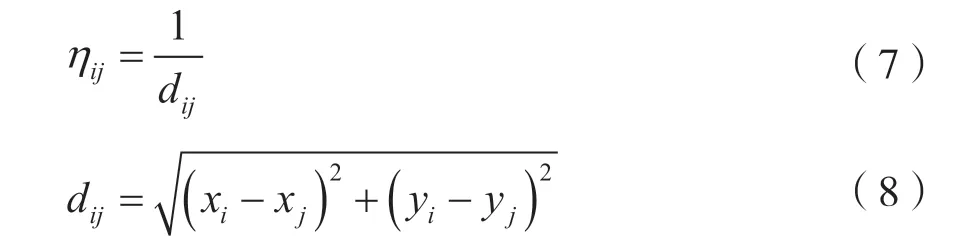
为了避免蚂蚁k选择走过的点，采用禁忌表tak记录蚂蚁k当前走过的节点。当所有蚂蚁都完成一次循环后，计算每只蚂蚁走过的路径长度lk，并保存最短路线，更新信息素τij，进行下一次循环，直到达到最大循环次数M。

信息素的更新公式为：

式中，ρ为信息素挥发系数，且0＜ρ≤1。

式中，是第k只蚂蚁在路径(i,j)上释放的信息素[13]，定义为：

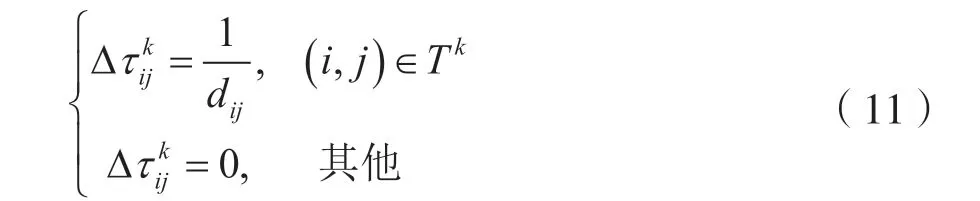
式中，Tk为第k只蚂蚁的路径集合。

蚂蚁完成一次循环后，清空禁忌表，重新回到初始位置，准备下一次迭代。算法流程如图4 所示。

3 算法仿真与分析

为分析两种算法的适应性，本文的仿真平台如下：计算机CPU 为Inter Core i7-8750H（2.2 GHz），内存为8 GB，显卡为NVIDIA GeForce GTX1050Ti，仿真软件为Matlab 2018b。首先设置算法的初始参数，其中A*算法的启发距离为欧几里得距离，蚁群算法的参数设置如表1 所示，Q为信息素增强因子。

分别在3 种实验环境下，对A*算法和蚁群算法进行仿真分析。

环境1 的参数设置如表2 所示。

图4 蚁群算法流程

表1 蚁群算法仿真实验参数

表2 环境1 模型参数

在此环境下，障碍栅格占空比即环境障碍阈值为0.33，分别进行10 次路径规划，结果如表3 所示。表3 中，l1、l2分别表示A*算法和蚁群算法找到的最短路径长度，x1表示蚁群算法找到最短路径时的迭代次数。对比两种算法的运行平均时间，A*算法比蚁群算法快9.612 s，蚁群算法较A*算法规划的路径平均值减少3.18。相比图5 图6 蚁群算法规划的路径平滑，转折少，且10 次实验中均规划出最短路径36.38。10 次实验中，算法最佳收敛曲线如图7 所示，找到最短路径的平均迭代次数为15.1 次，两种算法所得的安全代价分别为40.354 s和46.786 s。因此，在此环境应优先选用A*算法。

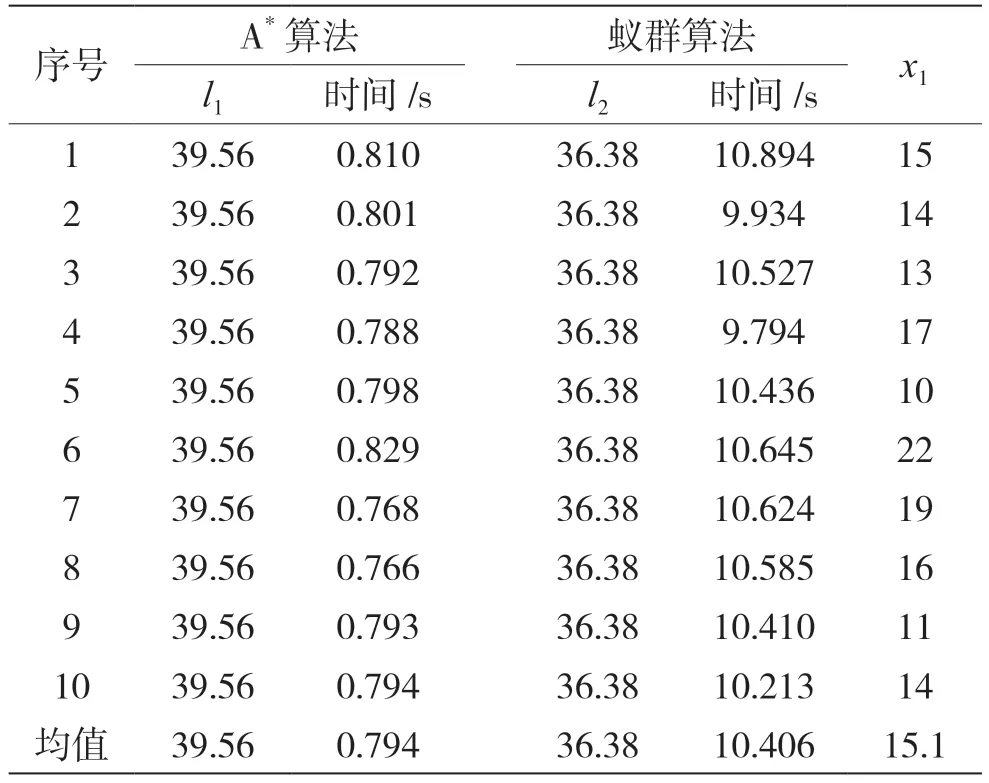
表3 环境1 下A＊算法和蚁群算法结果比较

图5 环境1 下A*算法结果

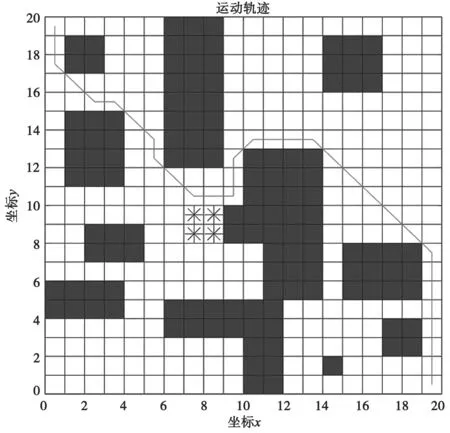
图6 环境1 蚁群算法结果

图7 环境1 蚁群算法收敛曲线

环境2 的参数设置如表4 所示。

表4 环境2 模型参数

在此环境下，环境障碍阈值为0.36，两种算法的10 次仿真结果如表5 所示。表5 中，l3、l4分别表示A*算法和蚁群算法找到的最短路径长度，x2表示蚁群算法在最短路径时的迭代次数。

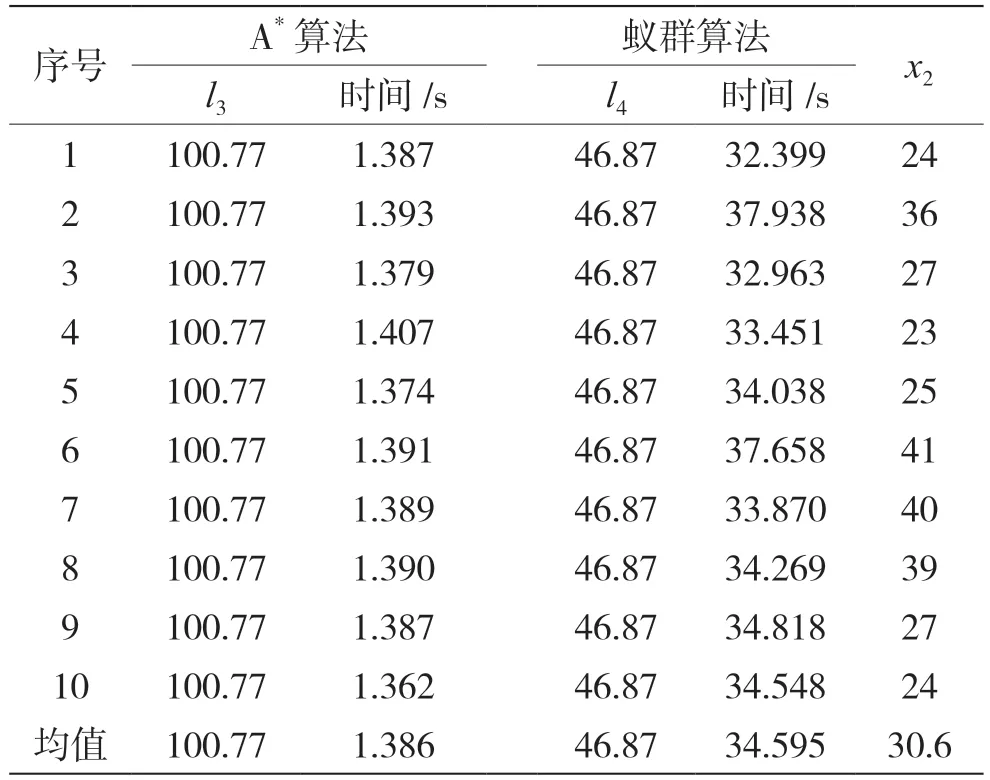
表5 环境2 下A＊算法和蚁群算法结果比较

对比两种算法计算时间，A*算法平均用时远小于蚁群算法，减小了33.209 s；规划出的路径平均长度，蚁群算法路径较A*算法大幅缩短，缩短了53.9，降幅达53.5%，且找到最短路径46.87；找到最短路径的平均迭代次数为30.6 次。图8 中，A*算法规划的路线相比图9 路径多次陷入局部最优，路径曲折往复，长度增加较多，不利于火场紧急环境下的人员逃生指引。A*算法和蚁群算法计算所得的安全代价分别为102.156 s 和81.465 s。实验中，算法最佳收敛曲线如图10 所示。考虑到蚁群算法规划的路径远离火情区域且安全代价较小，故在此环境中应优先选用蚁群算法。

图8 环境2 下A*算法结果

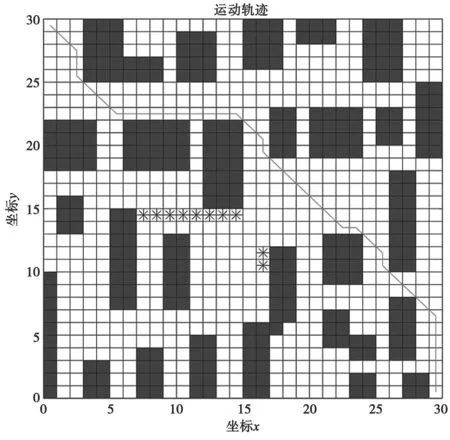
图9 环境2 蚁群算法结果

环境3 的参数设置如表6 所示。

在此环境下，环境障碍阈值为0.45，两种算法的10 次实验结果如表7 所示。表7 中，l5、l6分别表示A*算法和蚁群算法找到的最短路径长度，x3为蚁群算法在最短路径时的迭代次数。其中，A*算法运行时多次陷入死胡同，无法规划出路径；蚁群算法平均用时40.224 s，找到的最短路径为66.28，平均值为67.86，每次迭代找到最短路径的平均次数为33.1 次，如图11 所示。

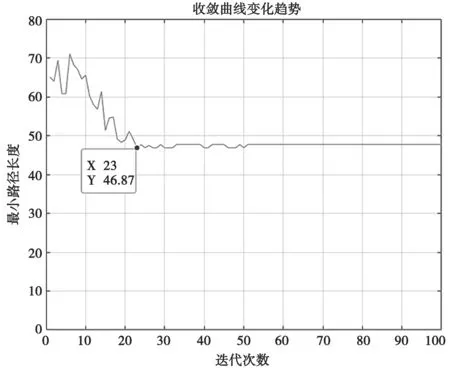
图10 环境2 下蚁群算法收敛曲线

表6 环境3 模型参数

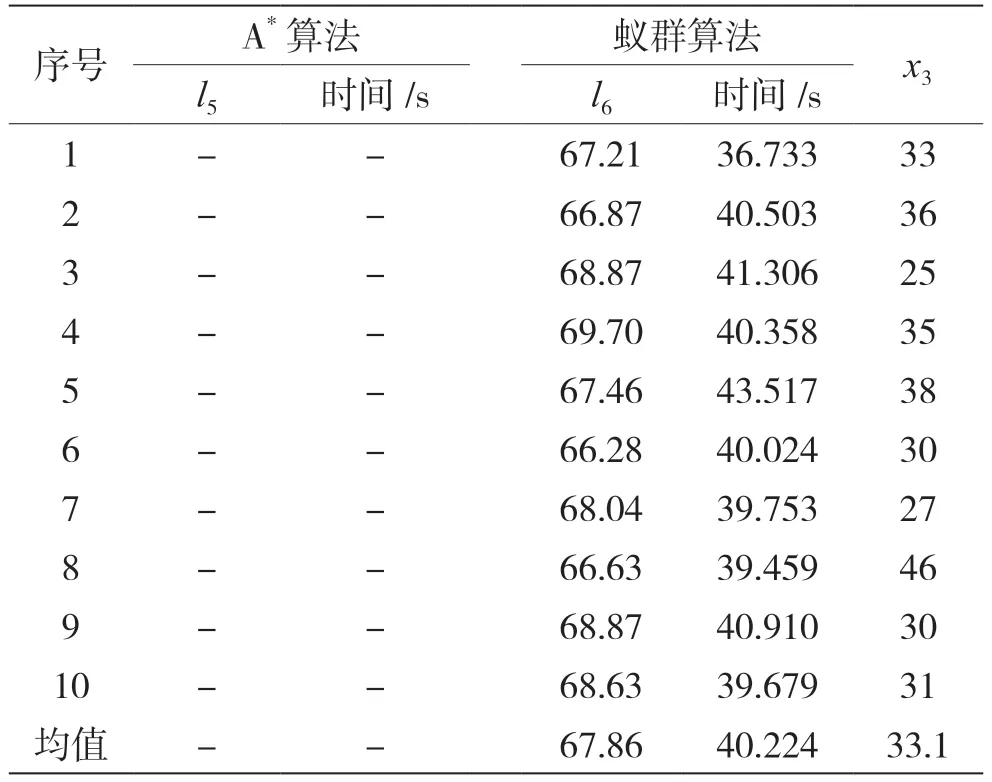
表7 环境3 下A＊和蚁群算法结果比较

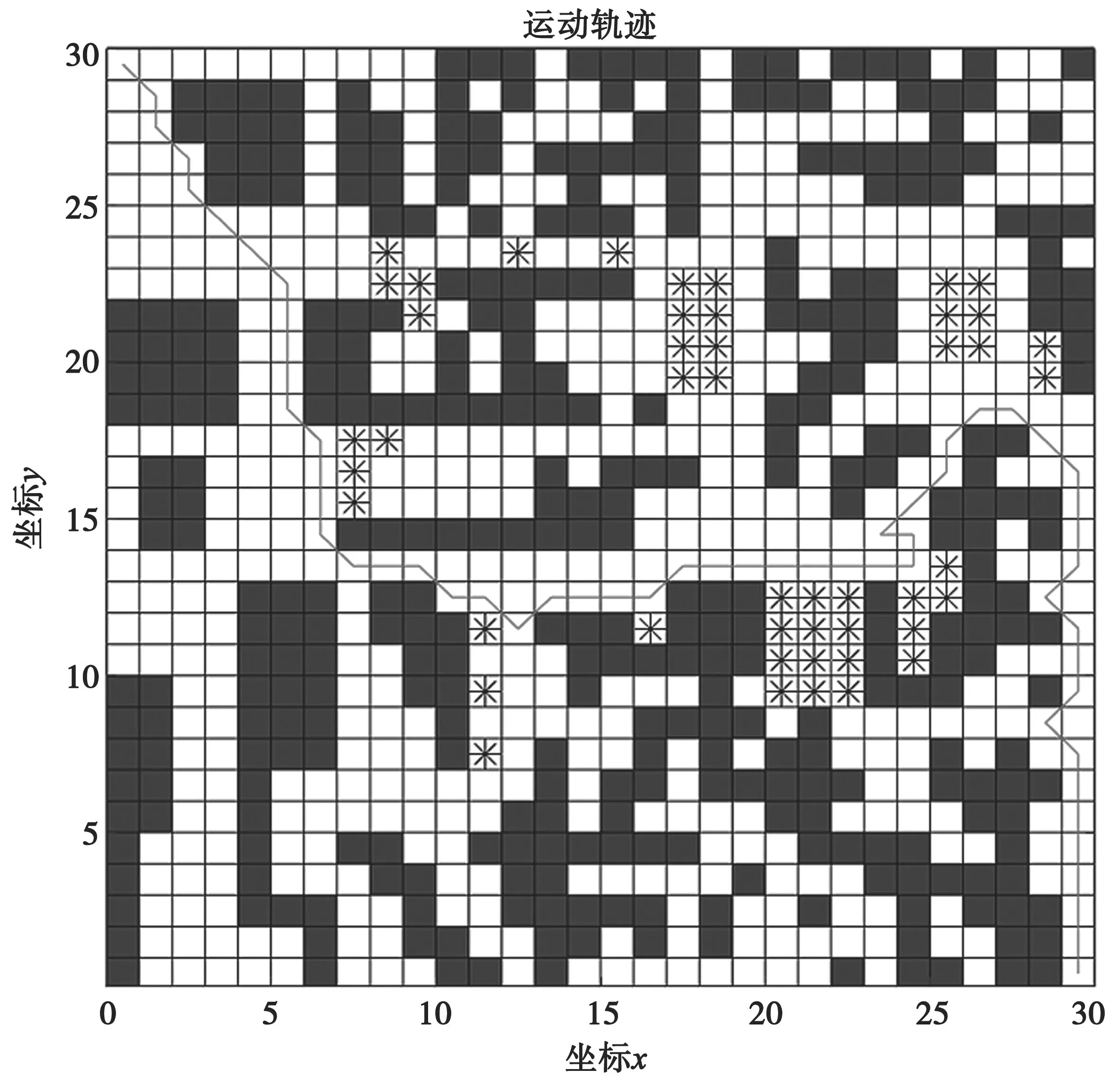
图11 环境3 蚁群算法结果

因环境障碍物较多且分布复杂凌乱，A*算法规划不出路径，而蚁群算法规划出的路径较曲折。如图12 所示，蚁群算法收敛曲线中前段为0 的部分是蚂蚁开始搜索迭代未找到路线的情况，经过一段时间的迭代与搜索，蚂蚁最终找到起点至终点的路径。A*算法和蚁群算法所得的安全代价分别为∞和108.084 s。在此种情况下，必须选用蚁群算法。

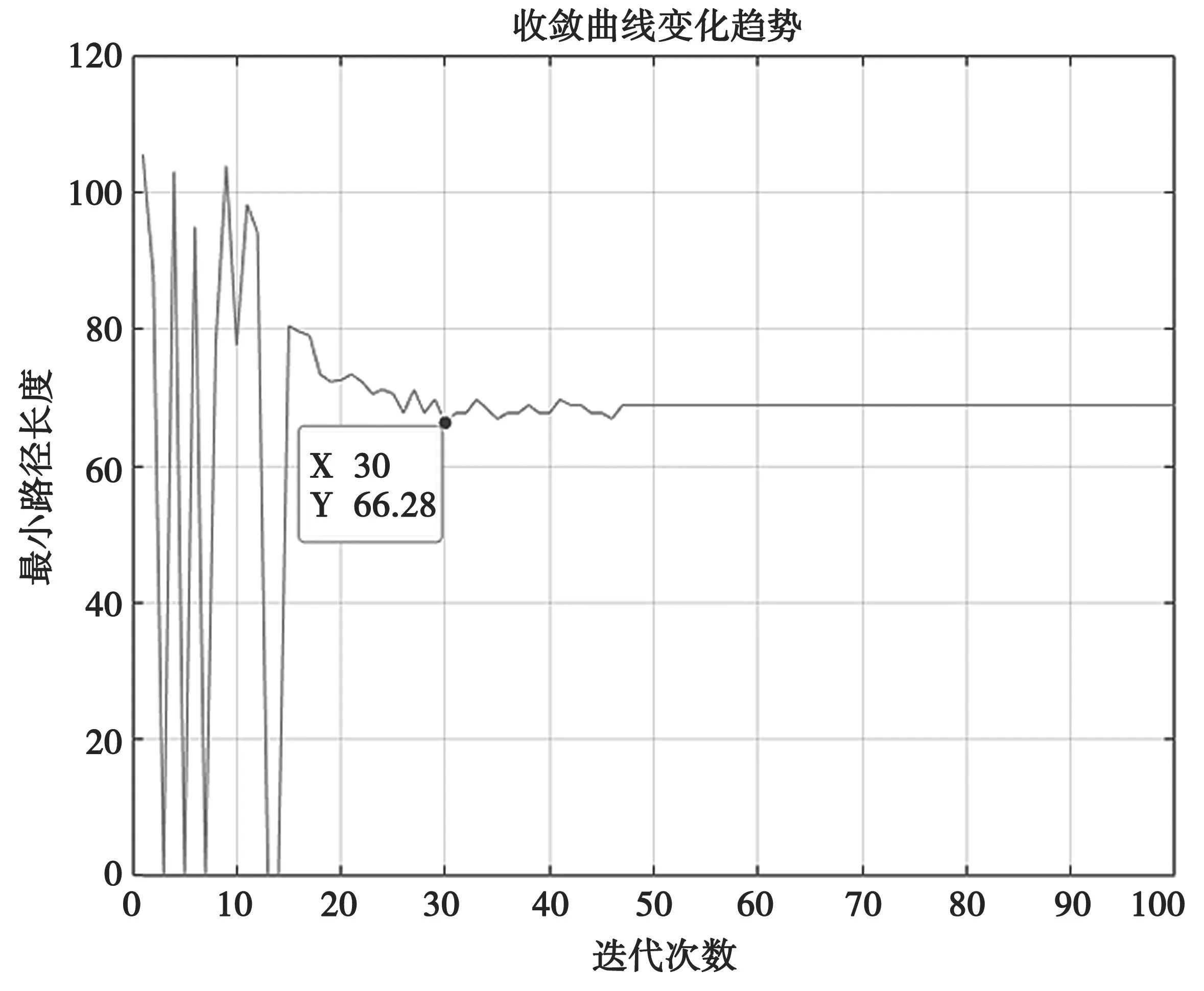
图12 环境3 蚁群算法收敛曲线

4 结语

通过对不同环境的仿真结果分析可知，当地图模型相对简单即环境障碍阈值为0.33 时，A*算法计算量小，算法运行速度快，可快速规划出路线。当环境规模增大且障碍物增多即环境障碍阈值为0.36 时，A*算法计算出的路径较曲折，相比蚁群算法，路径长度增加较多，此时对比路径权重和算法时间权重，选择最易通行的蚁群算法路径。当环境规模较大且障碍物分布相对复杂即环境障碍阈值为0.45 时，相比A*算法极易陷入局部最优，规划不出路径。蚁群算法在相同参数下需要多次迭代，规划的路径长度有波动，路线不固定。综上所述，通过对比分析，可为火灾逃生中选用合适的路径算法提供参考。